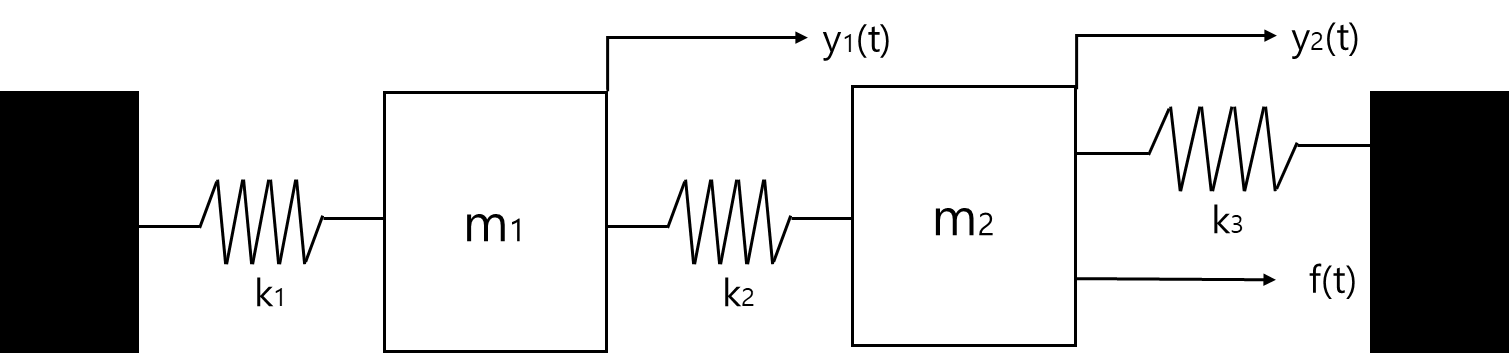2.1 Feedback Control(Closed-loop Control)
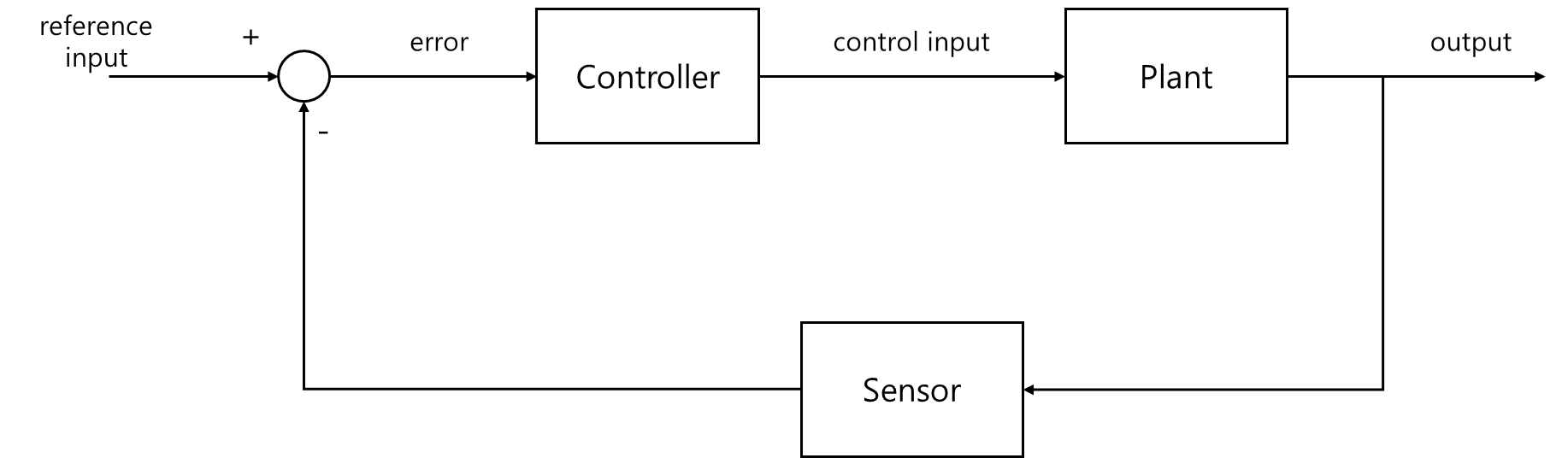
2.1.1 Objectives of Feedback Control
- 시스템의 dynamic response을 원하는 특성으로 변경
- closed-loop system이 안정적임을 보장
- 허용 가능한 과도 응답(transient response)와 정상 상태 응답(steady-state response) 얻기
- 방해 제거
※ 과도 응답과 정상 상태 응답
과도 상태(transient state) 는 시스템이 외부 입력이나 상태 변화에 반응하여 일시적으로 불안정한 상태를 겪는 기간을 의미한다. 주로 시스템에 새로운 입력이 인가되었을 때, 초기에는 불안정하거나 변화가 크지만, 시간이 지나면서 점점 안정된 상태(정상 상태; steady-state) 에 도달하기 전까지의 상태를 말한다.
2.2 How to design a good controller?
좋은 controller을 설계하기 위해서는, 시스템의 동작을 원하는 목표에 맞추기 위해 그 동작을 예측하거나 이해해야 한다. 설계는 다음의 과정을 거친다.
2.2.1 Modelling
모델링이란 시스템을 수학적으로 묘사하는 것이다. 주로 Ordinary differential equations(ODEs)가 사용된다. 모델링 자체만으로도 독립적인 학문 분야이며, George E.P. Box는 다음의 말을 하였다.
All models are wrong, but some are useful.
2.2.2 Modelling of Mechanical Systems
기계 시스템은 직선 운동, 회전 운동, 또는 이 두 가지의 조합으로 구성된다. 이 운동은 뉴턴의 운동 법칙으로 정의될 수 있다. 여기서는 주로 선형 및 평면 입자와 강체를 다룰 것이다.
Translational motion - Newton's Second Law

f=ma
⇔f(t)=ma(t)=mdt2d2y(t)
Translational motion - Lienar Spring

Fs=ky(t) 여기서 k는 spring constant 또는 stiffness이다.
Translational motion - Free Body Diagram(FBD)

∑F=ma
⇔f(t)−Fs=mdt2d2y(t)
my¨(t)+ky(t)=f(t); ODE
Translational motion - Friction
마찰 성분은 점성 마찰(viscous friction) 또는 점성 감쇠(viscous damping)로 근사된다. 점성 감쇠에서는 작용하는 힘과 속도가 선형적으로 비례한다.

여기서 b는 viscous damping coefficient이다.
Fd=bdtdy(t)=by˙(t)
위 운동을 F.B.D로 나타내면 다음과 같다.

∑F=ma(t)=my¨(t)=f(t)−Fd−Fs
⇔my¨(t)=f(t)−by˙(t)−ky(t)
⇔my¨(t)+by˙(t)+ky(t)=f(t)
Example
Consider the two degree of freedom mechanical system.
위 그림에 대해 F.B.D로 나타내면 다음과 같다.

여기서는 y1<y2라 하겠다.
m1y1¨(t)=Fd−Fs=b(y2˙(t)−y1˙(t))−ky1(t)
m2y2¨(t)=f(t)−Fd=f(t)−b(y2˙(t)−y1˙(t))
⇔
m1y1¨(t)−b(y2˙(t)−y1˙(t))+ky1(t)=0
m2y2¨(t)+b(y2˙(t)−y1˙(t))=f(t)
Example
Consider the two degree of freedom mechanical system.
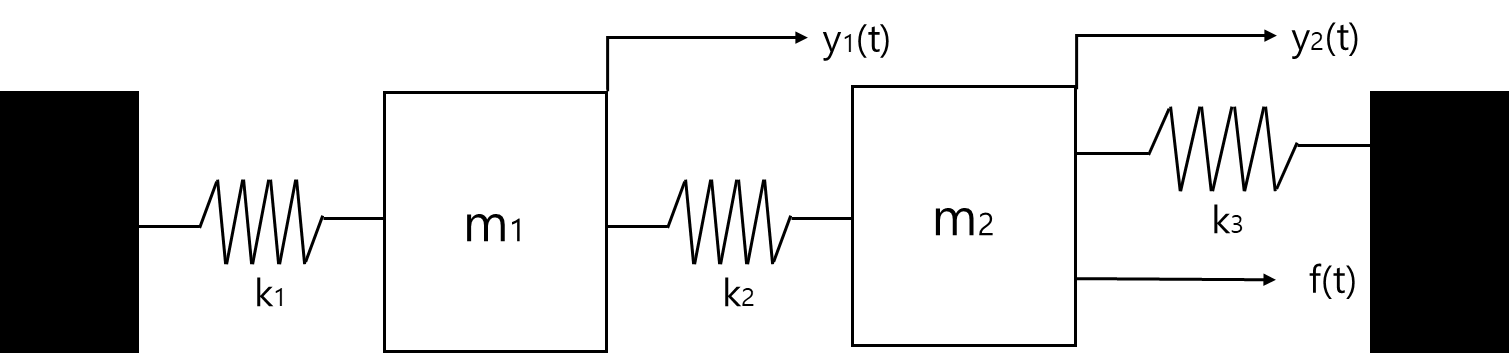
여기서는 y1(t)<y2(t)라 하겠다. 위 그림에 대한 F.B.D은 다음과 같다.

m1y1¨(t)=Fs2−Fs1=k2(y2(t)−y1(t))−k1y1(t)
m2y2¨(t)=f(t)−Fs3−Fs2=f(t)−k3y2(t)−k2(y2(t)−y1(t))
⇔
m1y1¨(t)+(k1+k2)y1(t)−k2y2(t)=0
m2y2¨(t)−k2y1(t)+(k2+k3)y2(t)=f(t)
Rotational motion - Newton's Second Law for rotational motion
∑External(Moments)=Jα
여기서 J는 inertia(관성) 을, α는 각가속도를 의미한다.
※ Inertia?
질량 m을 가진 강체는 고정된 회전축에 대해 관성 J를 가지며, 이는 회전 운동의 운동 에너지와 관련된 속성이다.
Example:
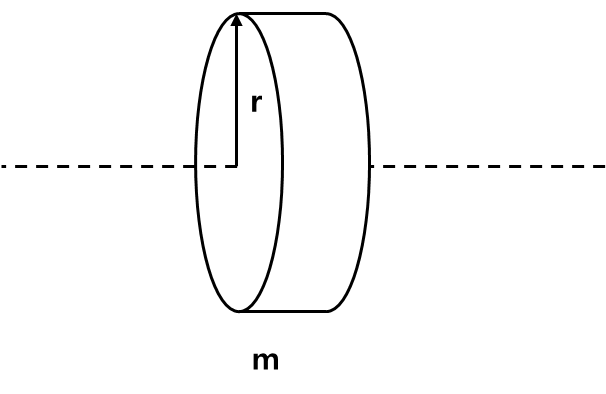
J=21mr2
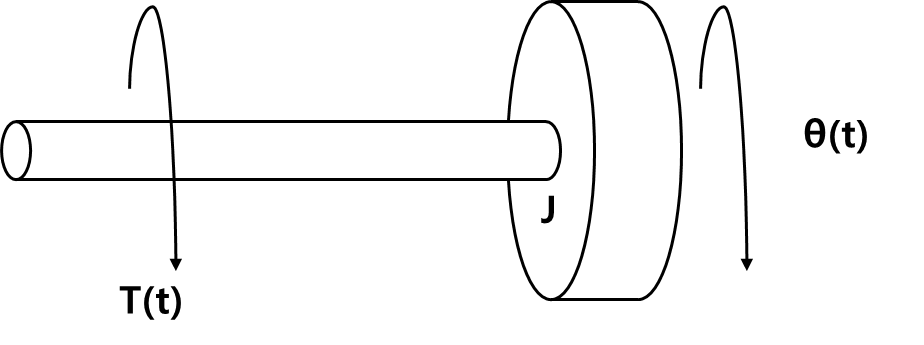
∑(Moments)=T(t)=Jα
⇔Jdt2d2θ(t)=T(t)
⇔Jθ¨(t)=T(t)
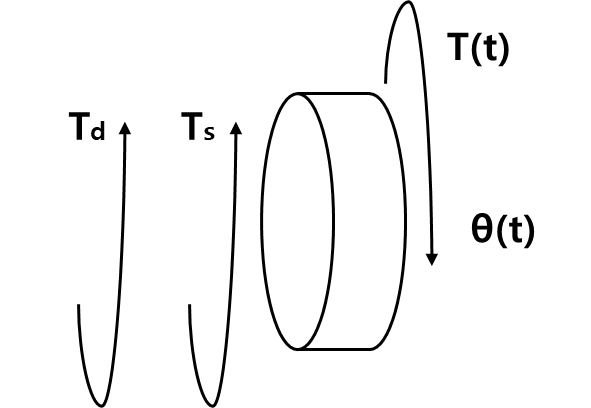
Torsional spring(비틀림 스프링)
회전 운동에서 토크를 제공하는 스프링이다. 이 스프링은 비틀림각에 비례하여 회전하는 물체에 저항하는 토크를 생성한다. 즉, 스프링이 비틀어지면 비틀림각에 따라 복원력을 제공하는 원리를 이용한다.
Ts=kθ(t)
Viscous damping for rotational motion(회전 운동에서의 점성 감쇠)
회전하는 물체에 작용하는 저항이 각속도에 비례하는 방식으로 발생하는 감쇠 현상을 일컫는다. 이 감쇠는 회전하는 시스템에서 마찰력이나 저항력이 존재하여, 물체의 회전 운동이 점차 줄어들고 멈추게 만드는 역할을 한다.
Td=bdtdθ(t)
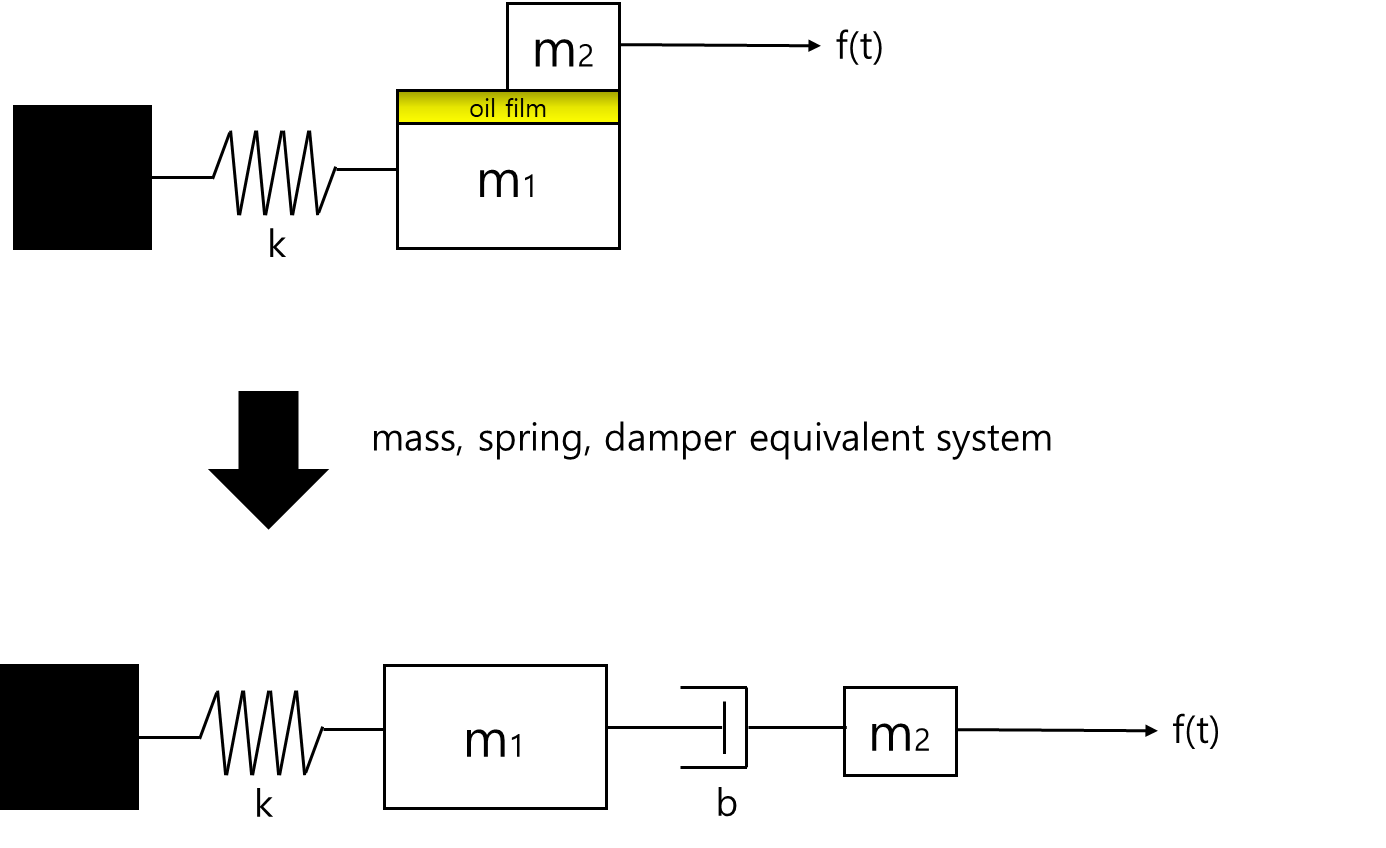
Example: Equivalent
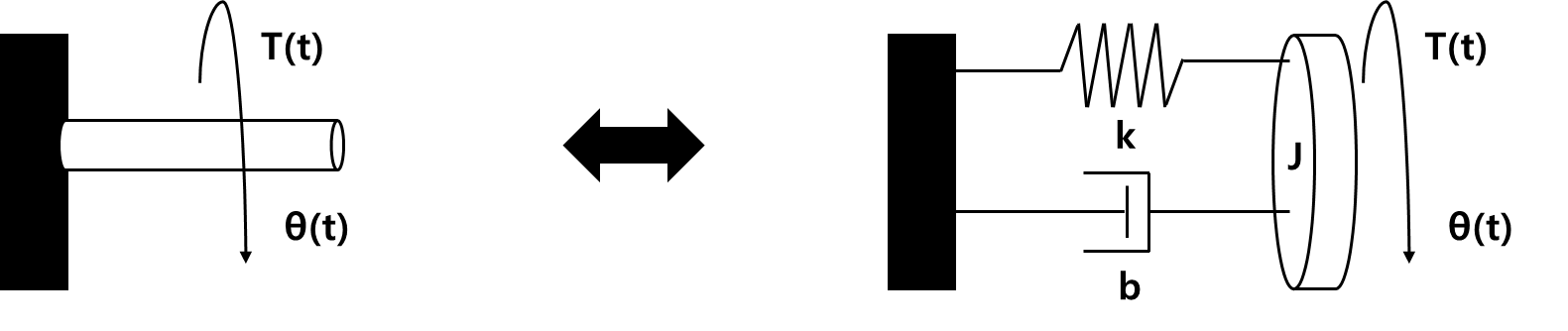
F.B.D
T(t)−Td−Ts=Jθ¨(t)
⇔Jθ¨(t)=T(t)−bθ˙(t)−kθ(t)
⇔Jθ¨(t)+bθ˙(t)+kθ(t)=T(t)
2.2.3 Why we learn mass-spring-damper system?
대다수의 기계 시스템은 mass-spring-damper 시스템으로 근사화될 수 있다.
Example: Flexible structure

Example: Vehicle suspension system(yc>yw>y)
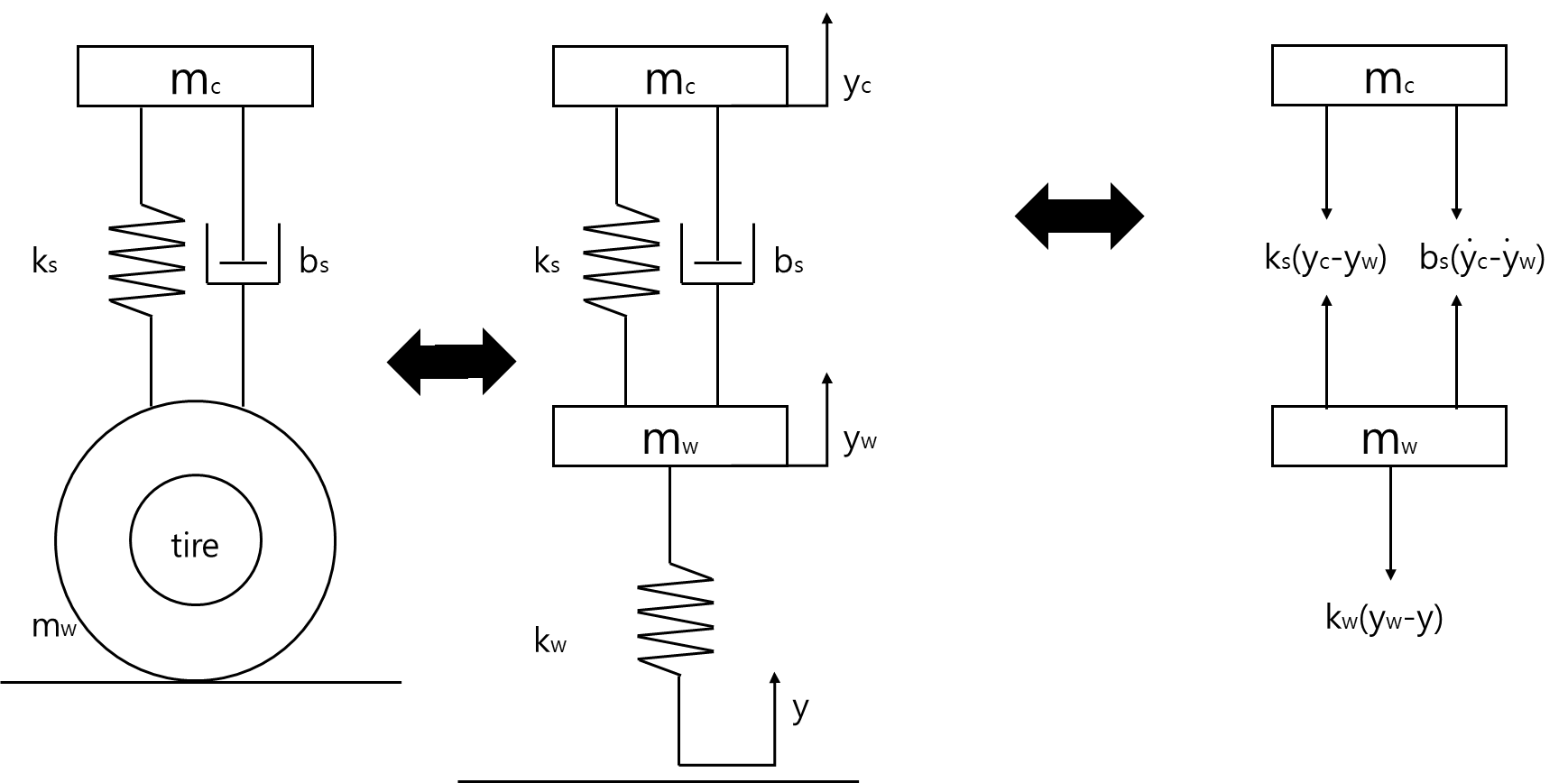
mwyw¨=ks(yc−yw)+bs(yc˙−yw˙−kw(yw−y))
mcyc¨=−ks(yc−yw)−bs(yc˙−yw˙)
⇔
mwyw¨+bs(yw˙−yc˙)+ks(yw−yc)+kwyw=kwy
mcyc¨+bs(yc˙−yw˙)+ks(yc−yw)=0
2.2.4 Summary of Mechanical system Modelling
- 필요하다면 mass-spring-damper system으로 근사하여 등가 모델을 구축하라.
- F.B.D을 그려라.
- 뉴턴 제2법칙을 적용하라.
<참고 문헌>
전웅선 교수님, 자동제어, 중앙대학교 전자전기공학부, 2024