3.1 Modeling of Electrical Components
3.1.1 Resistor
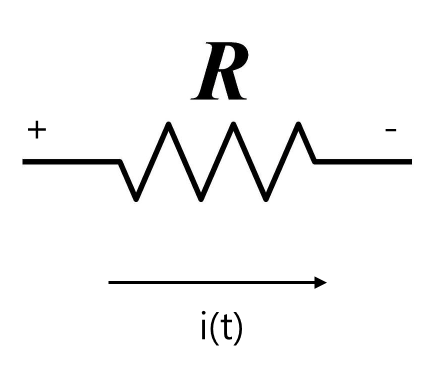
eR(t)=i(t)R
저항 R에 걸리는 전압 강하 eR(t)는 저항을 흐르는 전류 i(t)에 비례한다.
3.1.2 Inductor
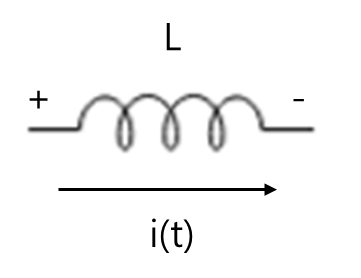
eL(t)=Ldtdi(t)
인덕터 L에 걸리는 전압 강하 eL(t)는 인덕터를 흐르는 전류 i(t)의 시간에 따른 변화율에 비례한다.
3.1.3 Capacitor
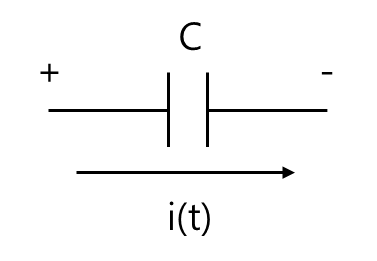
eC(t)=∫Ci(t)dx
커패시터 C에 걸리는 전압 강하 eC(t)는 전류 i(t)의 시간에 대한 적분에 비례한다.
3.1.4 Two Laws of Kirchhoff
Current Law: 어떤 노드로 들어오는 모든 전류의 산술합은 0이다.
Voltage Law: complete closed loop 내 모든 전압 강하의 산술합은 0이다.
Example 1: RLC network
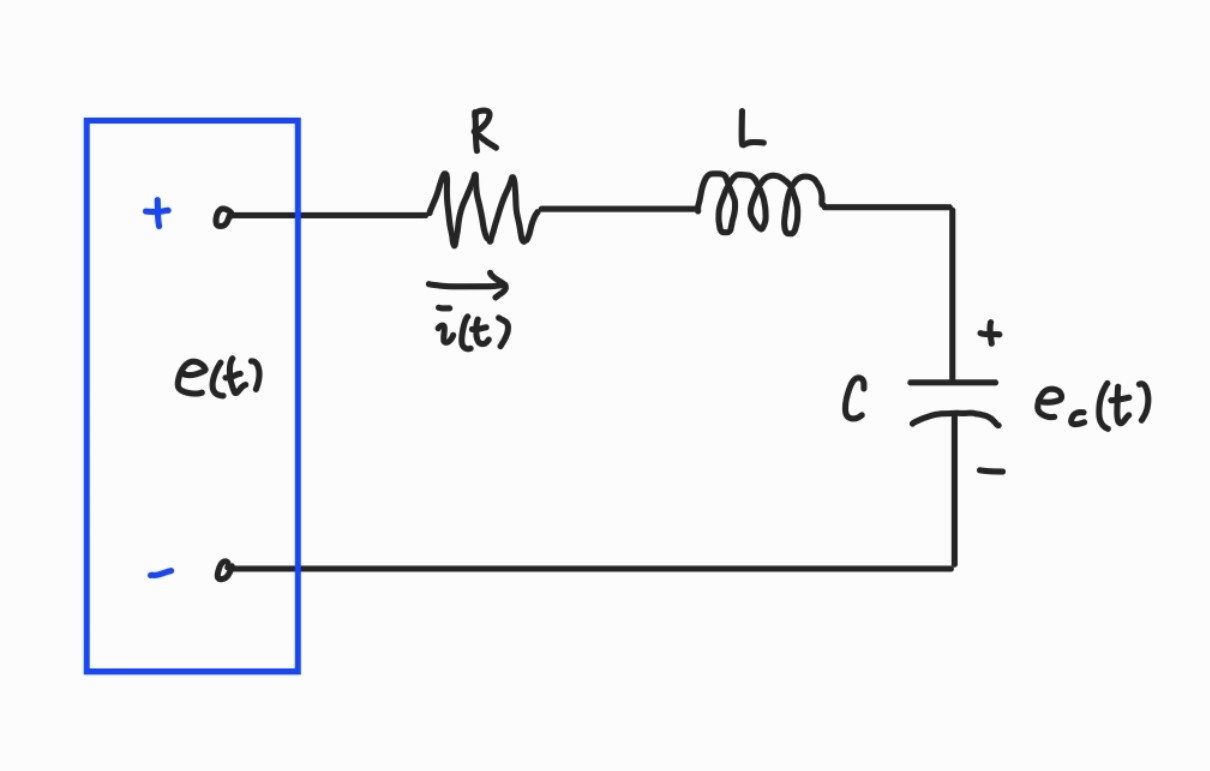
Voltage Law에 의해, e(t)−eR(t)−eL(t)−eC(t)=0
⇔e(t)=eR(t)+eL(t)+eC(t)
⇔e(t)=Ri(t)+Ldtdi(t)+eC(t)
여기서 eC(t)=∫Ci(t)dx→i(t)=CdtdeC(t)이므로
e(t)=RCdtdeC(t)+Ldt2d2eC(t)+eC(t)
∴LeC¨(t)+RCeC˙(t)+eC(t)=e(t)
여기서 eC(t)을 출력으로, e(t)을 입력으로 정의하였다.
Example 2:
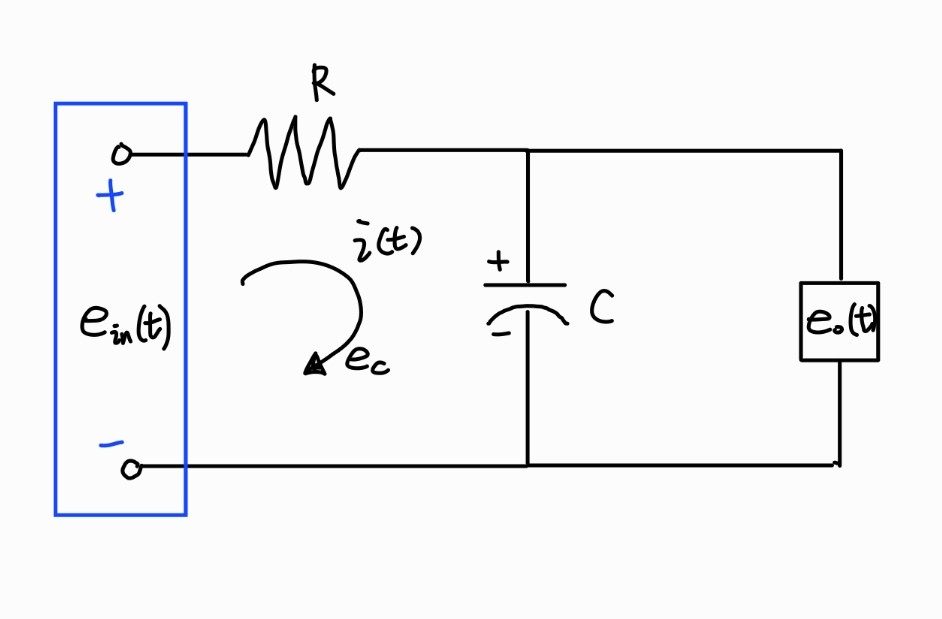
Voltage Law에 의해,
ein(t)=eR(t)+eC(t)=Ri(t)+C1∫i(t)dx
eC(t)=eo(t)=C1∫i(t)dt
⇔dtdeo(t)=C1i(t) ⇔Ceo˙(t)=i(t)
⇒ein(t)=RCeo˙(t)+eo(t)
∴eo˙(t)+τ1eo(t)=τ1ein(t)
여기서 τ=RC는 time constant이다.
Example 3:
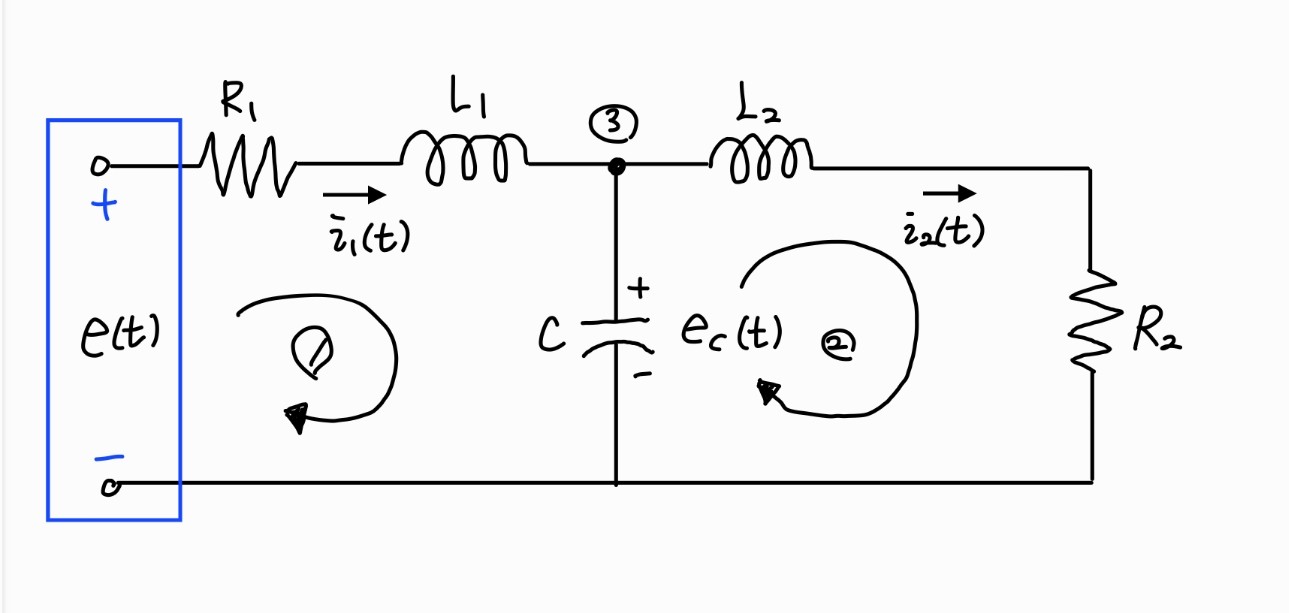
①: L1dtdi1(t)+R1i1(t)+eC(t)=et
②: L2dtdi2(t)+R2i2(t)=eC(t)
③: i1(t)=i2(t)+CdtdeC(t)⇔CdtdeC(t)=i1(t)−i2(t)
①, ② 양변을 미분하면
①: L1dt2d2i1(t)+R1dtdi1(t)+dtdeC(t)=dtde(t)
②: L2dt2d2i2(t)+R2dtdi2(t)=dtdeC(t)
③에 의해 정리하면,
①: L1dt2d2i1(t)+R1dtdi1(t)+C1(i1(t)−i2(t))=dtde(t)
②: L2dt2d2i2(t)+R2dtdi2(t)−C1(i1(t)−i2(t))=0
3.2 Modeling of Electromechanical(Mechatronic) Systems
Example: DC Servo Motor
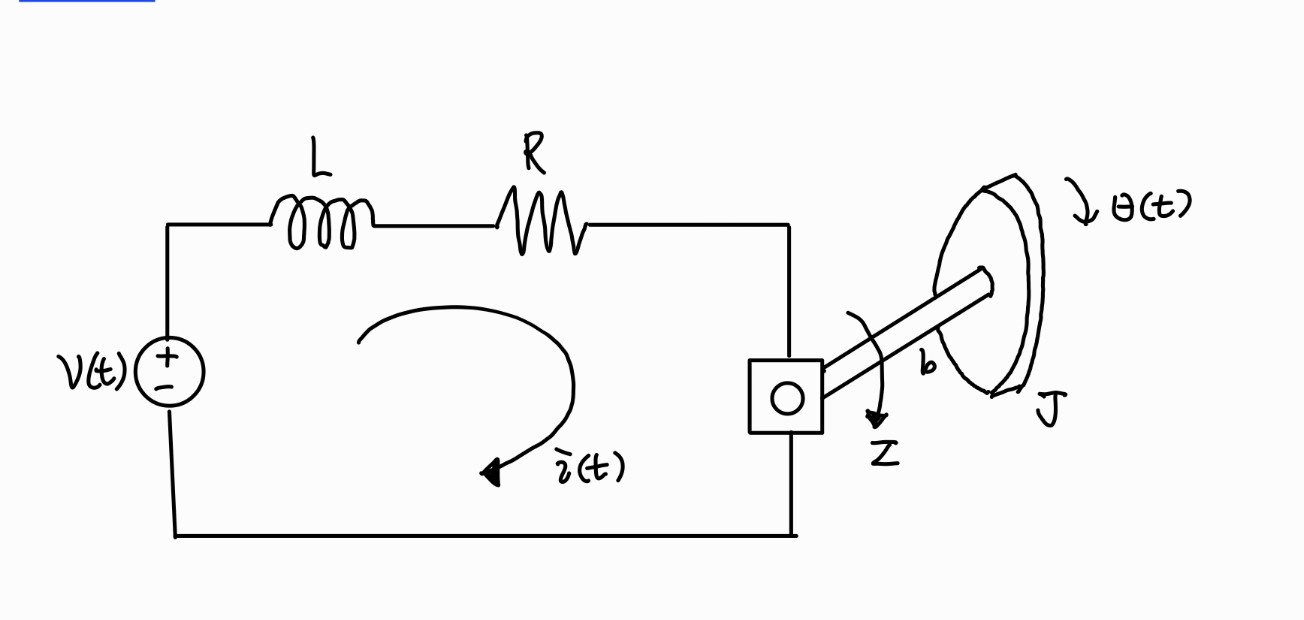
- Electrical Side
Ldtdi(t)+Ri(t)+eb(t)=V(t)
여기서 eb(t)=kbdtdθ(t) (back emf)이다.
- Mechanical Side
Jdt2d2θ(t)+bdtdθ=τ(t)
여기서 τ(t)=kmi(t)이다. 이는 기계 시스템과 전기 시스템의 관계를 나타낸다.
따라서
Ldtdi(t)+Ri(t)+kbdtdθ=V(t)
Jdt2d2θ(t)+bdtdθ=kmi(t)
<참고 문헌>
전웅선 교수님, 자동제어, 중앙대학교 전자전기공학부, 2024







