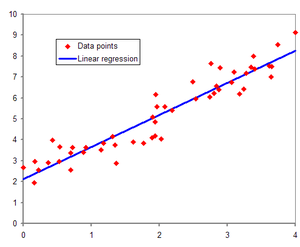
회귀분석의 개념
-
머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것이다.
- Y = W1 * X1 + W2 * X2라는 선형 회귀식을 예로 들면 W1, W2는 회귀계수이다.

- 예측의 정확도 판단
- 회귀 모델이 학습으로 찾은 함수를 가설 함수라고 하며, 예측 결과의 정확도를 판단하는 함수를 비용 함수라고 한다.
- 회귀 모델에서 비용 함수는 평균 제곱 오차 (MSE)가 사용되며, 가설 함수의 결과 (=예측값)와 실측값(=정답)의 오차 제곱의 합이 그것이다.
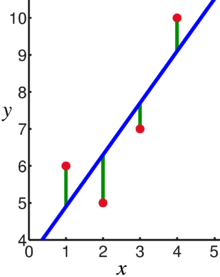
- 좌표계에서 평균 제곱 오차의 의미는 다음 그림으로 설명된다. 거리는 예측값과 실측값의 차이이며, 모든 데이터에 대해 이 값이 가장 작은 함수가 바로 찾고자 하는 가설 함수이다.
회귀 모델의 종류
회귀는 회귀 계수의 선형/비선형 여부, 독립변수의 개수, 종속변수의 개수에 따라 여러가지 유형으로 나눌 수 있다. 회귀에서 가장 중요한 것은 회귀 계수이며, 이 회귀 계수가 선형인지 아닌지에 따라 선형 회귀와 비선형 회귀로 나눌 수 있다. 그리고 독립변수의 개수에 따라 단일 회귀, 다중 회귀로 나뉜다.
여러가지 회귀 중에서 선형 회귀가 가장 많이 사용된다. 선형 회귀는 실제 값과 예측값의 차이를 최소화하는 직선형 회귀선을 최적화하는 방식이다.
선형 회귀 모델은 규제(Regularization) 방법에 따라 다시 별도의 유형으로 나눌 수 있다. 규제는 일반적인 선형 회귀의 과적합 문제를 해결하기 위해 회귀 계수에 패널티 값을 적용한 것을 말한다.
이들 중 릿지, 라쏘, 엘라스틱넷은 일반적인 선형회귀를 했을 때 독립변수 간에 상관성이 있는 경우 (다중공선성)에 사용된다.
(1) 일반 선형 회귀
예측값과 실제값의 RSS(Residual Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며, 규제(Regrularization)를 적용하지 않은 모델이다.
(2) 릿지(Ridge)
릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델이다. 릿지 회귀는 L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향을 감소시키기 위해 회귀 계수값을 더 작게 만드는 규제 모델이다
(3) 라쏘(Lasso)
라쏘 회귀는 선형 회귀에 L1 규제를 적용한 방식이다. L2 규제가 회귀 계수 값의 크기를 줄이는데 반해, L1 규제는 예측 영향력이 적은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것이다.
이러한 특성 때문에 L1 규제는 피처 선택 기능으로도 불린다.
(4) 엘라스틱넷(LeasticNet)
L1, L2 규제를 함께 결합한 모델이다.
주로 피처가 많은 데이터 셋에서 적용되며, L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수 값의 크기를 조정한다.
(5) 로지스틱 회귀(Logistic Regression)
로지스틱 회귀는 회귀라는 이름이 붙어 있지만, 사실은 분류에 사용되는 선형 모델이다. 로지스틱 회귀는 매우 강력한 분류 알고리즘이다. 일반적으로 이진 분류뿐만 아니라 희소 영역의 분류, 예를 들어 텍스트 분류와 같은 영역에서 뛰어난 예측 성능을 보인다.
회귀 평가 지표
회귀의 평가를 위한 지표는 실제값과 회귀 예측값의 차이값을 기반으로한 지표가 중심이다.
실제값과 예측값의 차이를 단순히 더하면 +와 -가 섞여서 오류가 상쇄된다.
예를들어 데이터 두 개의 예측 차이가 하나는 -3, 다른 하나는 +3일 경우 단순히 더하면 오류가 0으로 나타나기 때문에 정확한 지표가 될 수 없다. 따라서 오류의 절대값 평균이나 제곱, 또는 제곱한 뒤 다시 루트를 씌운 평균값을 구한다. 일반적으로 회귀의 성능을 평가하는 지표는 다음과 같다.
| 평가 지표 | 설명 |
|---|---|
| MAE | 실제값과 예측값의 차이를 절대값으로 변환해 평균한 것 |
| MSE | 실제값과 예측값의 차이를 제곱해 평균한 것. 실제 오류 평균보다 더 커지는 특성이 있다 |
| RMSE | MSE에 루트를 씌운 것이다. |
| 분산 기반으로 예측 성능을 평가. 1에 가까울 수록 예측 정확도가 높다. |
사이킷런은 RMSE를 제공하지 않는다. 따라서 RMSE를 구하기 위해서는 MSE에 제곱근을 씌워서 계산하는 함수를 직접 만들어야 한다.
출처
https://movefast.tistory.com/302?category=866099
https://roytravel.tistory.com/57
