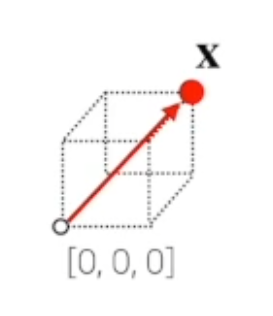
벡터

벡터는 숫자로 원소로 가지는 리스트 또는 배열 입니다.

벡터는 공간에서 한 점을 나타냅니다.
벡터는 원점으로부터 상대적 위치를 표현합니다.
원점 좌표에서 어떤 한점을 표현하는 화살표를 그림으로 표시하면!

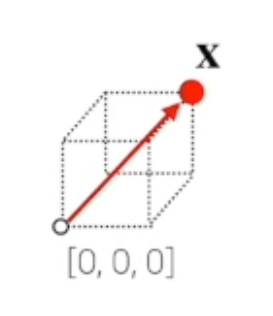
이런 개념으로 이루어져 있다.
어떠한 벡터에 스칼라(크기)를 곱하면 각각 고정성분에 그벡터의 길이만 변하게 된다.

벡터의 사칙연산

벡터끼리 같은 모양을 가지면 사칙연산을 계산할 수 있습니다.

벡터의 노름(norm)

원점에서부터의 거리를 말한다.
임의의 차원 d에서도 성립한다.
벡터의 차원에 상관없이 계산이 가능하다.

L1-노름은 각 성분의 변화량의 절대값을 모두 더합니다.

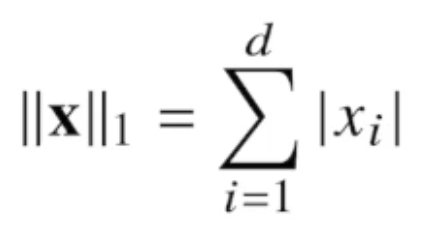
L2-노름은 피타고라스 정리를 이용해 유클리드 거리를 계산합니다.

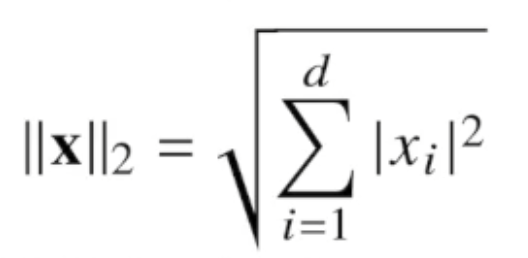
파이썬 numpy 에서 노름을 계산하는방법.

def 11_norm(x):
	x_norm = np.abs(x) # 절대값 
	x_norm = np.sum(x_norm) # 각자 더하기 
return x_norm

def 12_norm(x):
	x_norm = x*x # 제곱
	x_norm = np.sum(x_norm) # 각자 더하기 
	x_norm = np.sqrt(x_norm) # 스퀘어 루트 
return x_norm

노름을 소개하는 이유 : 노름의 종류에 따라 기하학적 성질이 달라진다.

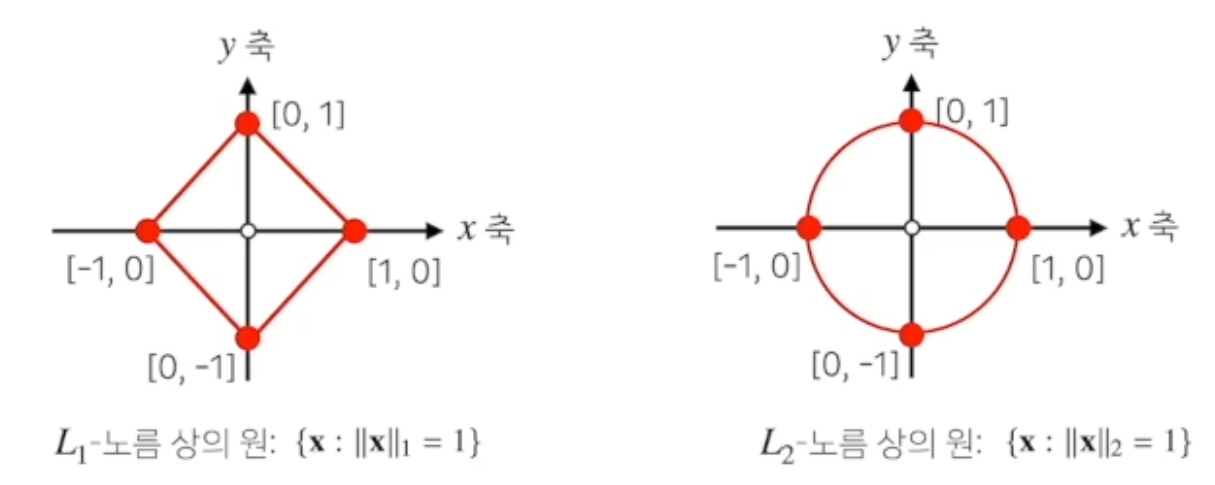
성질이 달라진 기하세계에서 학습을 진행할때 굉장히 다른 성질들이 나온다. 이 성질들을 이용해서 다양한 종류의 학습방법을 사용한다.

머신러닝에선 굉장히 다른 norm 들을 사용하기때문에 두가지 개념을 잘 알아두자.

두 벡터 사이의 거리를 구해보자!

L1, L2- 노름을 이용해 두벡터 사이의 거리를 계산 할 수 있다.

주로 두 벡터의 (절대값의)뺄셈을 사용한다.

그럼 두 사이의 거리를 이용해 각도도 계산해 볼 수 있을까?
주의 : L2노름만 사용할 수 있다.

제2 코사인 법칙에 의해 두벡터 사이의 각도를 계산할 수 있다.

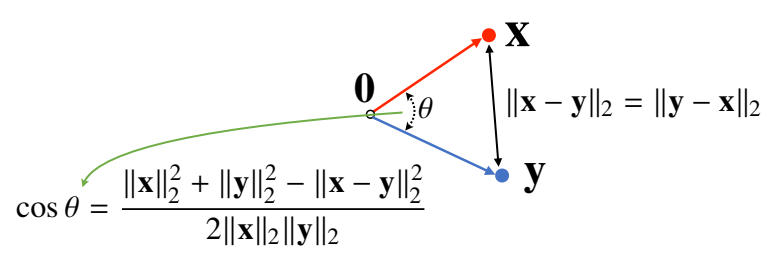
분자를 쉽게 계산하는 방법이 내적이다.

def angle(x,y) : 
	v=np.inner(x,y) / (12_norm(x) * 12_norm(y))
    theta = np.arccos(v)
    return theta

L1노름에서는 각도를 계산 할 수 없다!

내적은 어떻게 해석할까?

• 내적은 정사영(orthogonal projection)된 벡터의 길이와 관련 있다.
• Proj(x)의 길이는 코사인법칙에 의해 ||x||cos0 가 된다.

• 내적은 두벡터의 유사도(similarity)를 측정하는데 사용 가능하다.
• 정사영된 길이에 벡터 y만큼의 길이로 조절한다.

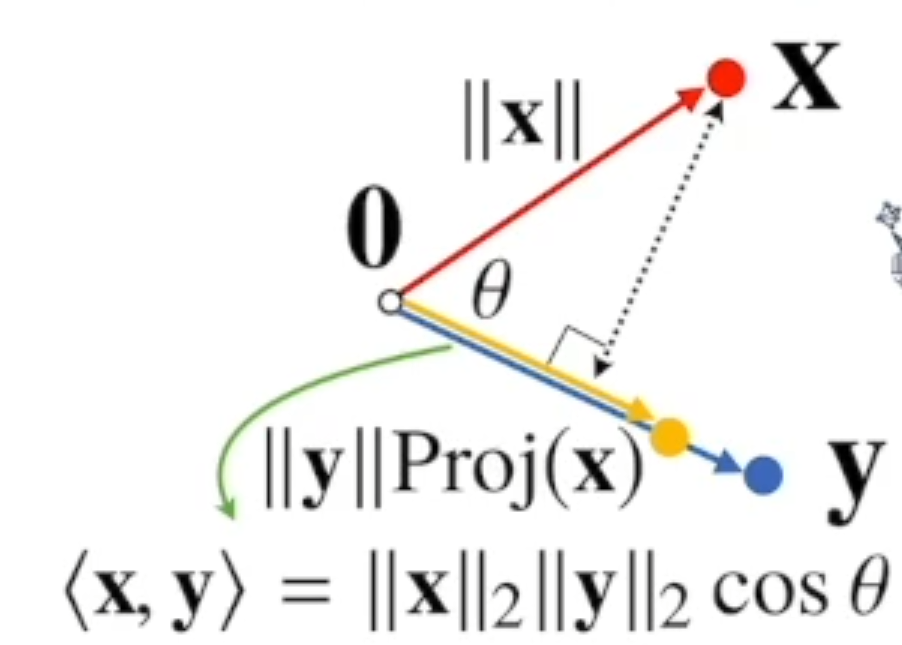
X벡터를 Y벡터 위에 그대로 투영해서 내릴때
Y벡터 입장에서 X벡터의 길이를 볼 수 있기 때문에 유사도를 측정 할 수있다.