Practical Gradient Method

• Stochastic gradient descent
  • 10만개의 데이터가있으면 1번에 1번의 보개로 gradient를 구하고 업데이트 한다.
• Mini-batch gradient descent
  • 10만개를 다쓰거나 1개만 쓰는게 아니다. 일반적인 batch사이즈로 128개, 256개 등으로 gradient를 구해서 업데이트 하고
• Batch gradient descent
  • 한번에 10만개 전부다 써서 10만개의 gradient를 다써서 업데이트를 한다.

보통 대부분은 Mini-batch를 사용한다.

Batch-size Matters

• 10만개를 쓰냐? 1개를쓰냐?

적절히 그 중간의 64개 128개를 활용하면 좋겠다 라는 생각이 많았는데
생각외로 Batch-size가 굉장히 중요하다.

• 관련 논문에서는 Batch-size를 엄청크게 쓰면 sharp minimizers에 도달한다고 한다.(뭔지는모름) 일반적으로 배치사이즈를 작게쓰는게 실험 성능에 좋다 라는게 말하고자 하는것.
  

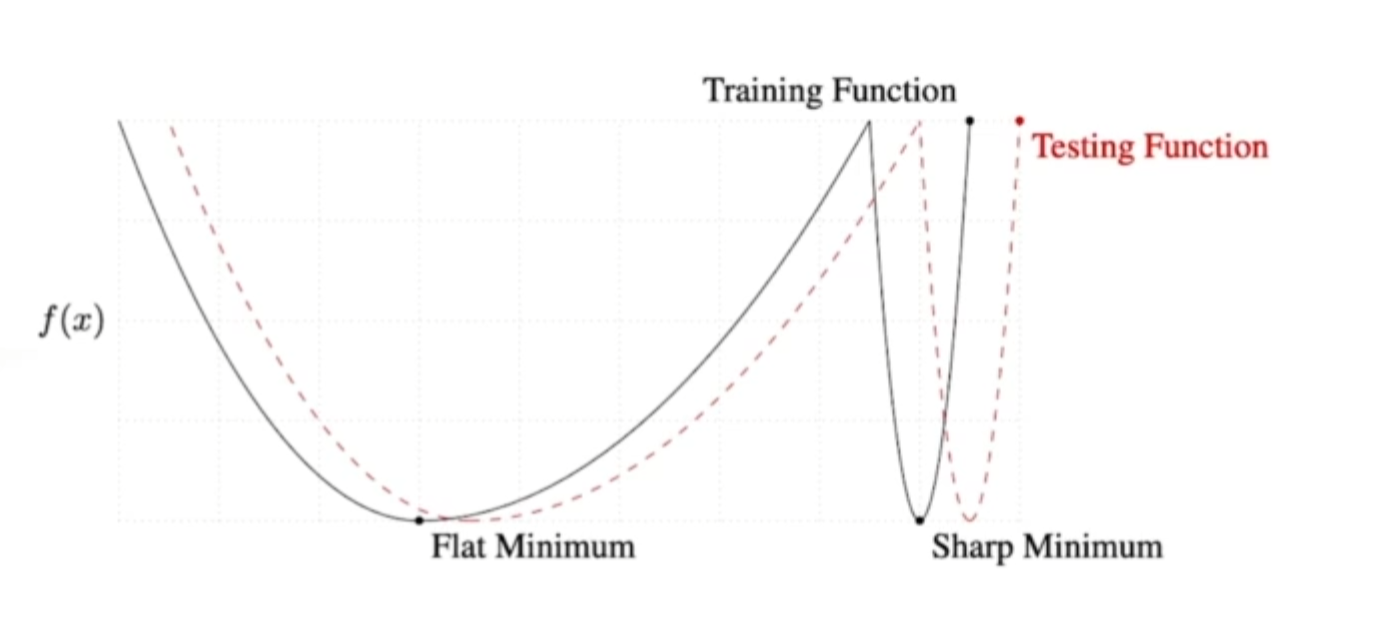
• sharp보다는, Flat minimum에 도달하는게 더 좋다라는 말이다.

• Flat미니멈의 특징은 트레이닝 펑션과 멀어져도, 파라미터가 조금 떨어져도 어느정도 값이 비슷하게 나오는 특징을 가지고 있다.

• 근데 Sharp의 경우는 미니멈값에서 조금만 멀어져도 테스트 펑션이 굉장히 높은값이 나올수잇다. ( 잘 동작을 안할 수 있다. )

실질적으로 Tensor flow, pytorch로 학습시킬때

• loss 펑션을 정의하고 이럴때 손미분으로 하지않는다. 그래서 자동적으로 미분을 제공해주는것을 사용한다.
• 그래서 Optimizer 를 정해줘야한다.

Stochastic Gradient descent

• Gradient Descent 를 하기 떄문에 Gradient를 구해준다. 이것이 G가 되고, 이 그레디언트를 η에타라고하는 러닝레이트만큼 곱해서 빼주면 update가 된다.
• 이 러닝레이트, step size를 잡는게 너무 어렵다.

Momentum

어떻게 더 좋은성능, 더 빨리 집에 가서 저녁이있는 삶을 살수있게 빨리 학습을 시킬수잇는 테크닉들이 나오게 된다.

그중 하나가 모멘텀이다.

한번 gradient 가 오른쪽으로 흐르면, 왼쪽 값이 들어와도 살짝 오른쪽 gradient로도 이동을 시키는 힘을 줄인다고 생각하자. 바로 왼쪽으로 바꾸지말고.

모멘텀 + 현재 gradient를 합친 값으로 업데이트를 시킨다.

Nesterov Accelerate Gradient

• NAG

• 그레디언트를 계산할때 Lookahead 그레디언트로 계산한다.
  한번 이동한다. A라는 방법으로 가보고 그 간 정보를가지고 update를 한다.
  

• 로컬 미니멈을 지나서 도착한 점에서 gradient를 계산하는게 아니라, 한번 지나간 그점에서 계산한다.

• 봉우리의 끝점에 좀 더 잘 도착하게 된다.

Adagrad

• 지금 가지 변한 gradient값을 저장해서 사용하고싶다.
• 많이 변한건 적게 변화시키고, 적게 변화시킨건 많이 변화시키겠다.
  

가장큰 문제는 G가 계속 커지기 때문에 무한대로 가게 되면 w의 업데이트가 안된다.

계속 G라고 불리는 그레디언트 값들을 해결하고자 다른 방법론들이 나오게됐다.

Adadelta

• Adagrad 가 가지는 단점을 해결하기 위한(G가 계속커지는현상) 방법론이다.
• 윈도우 사이즈 (t:시간) 만큼의 Gradient 제곱을 보겠다
• 하지만 문제가 생긴다. 1000억개의 파라미터를 사용한다고 하면 시간값까지 더해져 그래픽카드가 터져버리고만다
• 그래서 익스포넨셜 값을 사용한다.

  많이 활용되지는않는다. ( 러닝레이트가 없어서 )

RMSprop

• 이게 많이 사용이 됐었다.(과거형..?)
• Geoff Hinton 이 딥러닝 강의를하다가 이렇게 업데이트를 하다가 잘된다. 라고 강의중에 제안을 했다.
  실제로 해보니까 잘되길래 만들어졌다.
• Gradient를 EMA(익스포넨셜 민 에버레지)

Adam

• 일반적으로 가장 무난하고 잘되는게 Adam이다.

• Gradient의 크기가 변함에 따라 Adaptive하게 러닝레이트를 바꾸다, 이전에 Gradient 모멘텀 크기를 저장하는걸 합쳐서 적절히 사용하는것이다.

• 위에 나온 개념들을 다 합친 방식이다.

• 파란화살표는 수학적으로 사용되는 unbiased estimate용으로 들어간거다. 중요한값은아님.

• 실제론 저기에있는 엡실론 ε(약 10-7) 이 굉장히 중요하다. 이값을 바꾸는게 영향을 많이 미침.

총평

• 우리가 구현할 필요는 없고, pytorch, tensor 플로우에서 한줄만 바꾸면 알아서 돌아가게 된다.

후기 : 선생님이 말씀을 참잘하셔서 알아듣기 좋고 농담도 섞고 제스쳐도 쓰셔서 재밋다 !