
분류 (Classification)
: 주어진 데이터를 미리 정의된 클래스 레이블로 분류하는 문제를 다루는 기계 학습 방법
Q1) 응급실에 오는 환자는 3가지 의료상태 중 어느 하나에 의한 증상을 가지고 있다. 이 환자는 어느 상태인가?
Q2) 온라인 뱅킹 서비스는 사용자의 IP주소, 과거 거래이력 등을 바탕으로 현지에서 진행되고 있는 거래가 사기성인지 결정할 수 있어야 한다.
Q3) 다수 환자들에 대한 DNA 염기서열 데이터에 기초하여 생물학자는 어느 DNA 변이가 유해하고 어느 것이 그렇지 않은지 알아내고자 한다.
...
1. 로지스틱 회귀분석(Logistic Regression)
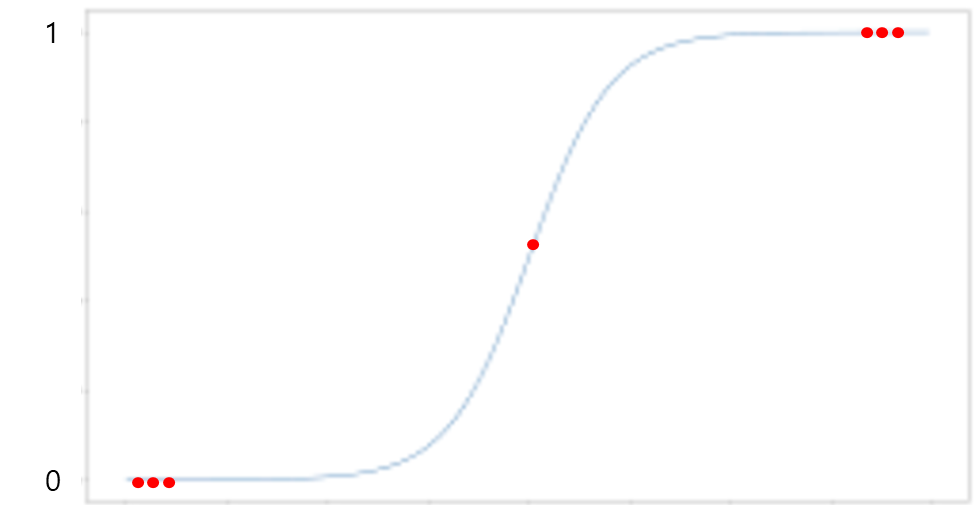
- 반응변수 y를 직접 모델링 하지 않음, y가 특정 범주에 속하는 확률을 모델링
- 로지스틱 함수를 사용하여 두 개의 반응변수 클래스에 대해 직접 모델링
p(x) = 1 / (1 + e^(-z))
2. 선형 판별 분석(Linear Discriminant Analysis, LDA)
: 클래스 간의 선형 경계를 찾고, 데이터를 그 경계로 분류하는 모델을 구축하는데 사용
- 반응변수 Y의 각 클래스에서 설명변수 X의 분포르 모델링, 베이즈 정리를 사용하여 추정치 얻음
- 로지스틱 회귀 대신 사용하는 이유
: 클래스들이 잘 분리될때 로지스틱 회로에 대한 모수 추정치는 아주 불안정. 선형판별 분석은 이러한 문제 없음
: 만약 n이 작고 각 클래스에서 설명변수 X의 분포가 근사적으로 정규분포이면 선형판별모델은 로지스틱 회귀모델보다 더 안정적
: 선형판별분석은 반응변수의 클래스 수가 2보다 클 때 일반적으로 사용
01. 분류를 위한 베이즈 정리의 사용
-
베이즈 정리
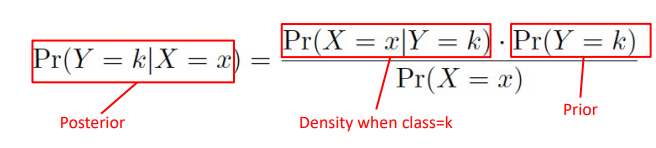
-Posterior probability : Predictor가 주어졌을 때 해당 class K의 확률
-Prior probability : Class K의 확률(아무것도 관찰된 것이 없을 때)
-Density function : X가 class K에 속할 경우, X의 확률 밀도 -
Logistic Regression와 Bayes Classifier
: Logistic Regression을 Bayes calssifier의 근사화로 생각할 수 있음
-Posterior probability를 다음 함수(linear regression + logistic function)로 근사화
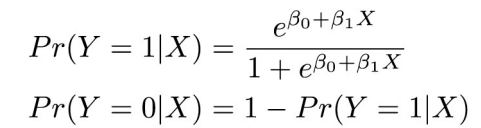
-Linear regression을 binary classifier로 확장시킨 것
-class별로 잘 분리되어 있거나 2개 class 이사일 경우 잘 맞지 않음
02. 판별 분석(Discriminant Analysis)
- 기본 아이디어
-각 class별로 X의 분포(distribution)를 모델링하고 Bayes theorem을 이용하여 P(Y|X)를 구함
-각 class에 대해 정규 분포(normal/gaussian distribution)를 사용하면, linear discriminant analysis (LDA)나 quadratic discriminant analysis (QDA)가 됨
3. 이차판별분석(QDA, Quadratic Discriminant Analysis)
: 데이터의 클래스를 분류하기 위해 이차식(Quadratic equation)을 사용하는 분류 모델
: 이차판별분석은 입력 데이터의 클래스 간 분산과 클래스 내 분산을 개별적으로 모델링하여 비선형 분류 문제에 적합한 유연한 모델을 구축하는 방법
01. LDA VS QDA
LDA
- 클래스 간 분산과 분산의 비율을 최대화하는 선형 판별 기준을 사용해서 차원 축소 수행
-> 선형 결정 경계를 기반으로 데이터 분류
-> 계산 비용 낮음, 과적합 감소
-> 클래스 간 분산이 작을 때 효과적
QDA
- 클래스 간 분산과 클래스 내 분산을 개별적으로 모델링
- 각 클래스마다 고유한 공분산 행령을 가정해서 사용하고 이는 데이터가 비선형 결정 경계를 가지는 경우에 유연성을 제공
-> 비선형 문제를 해결하는데 적합
-> 데이터셋이 복잡하고 클래스 간 분산이 큰 경우 유리
-> 계산 비용 큼, 작은 훈련 데이터셋에서 과적합 위험 높을 수 있음
4. K-nearest neighbors
- KNN
-non-parametric approach
-모델에 대한 가정 없음
-Decision boundar가 non-linear
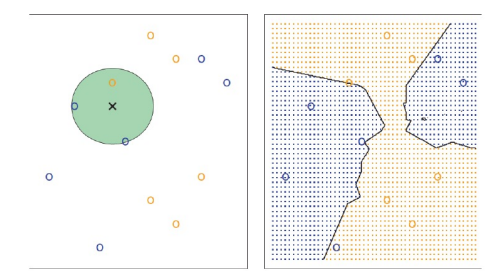
-장점 : flexibility
-단점 : inferece에는 부적합
5. Classification 기법 비교
- 어떤 분류 기법이 좋은가?
-> data에 따라 다름
01. Linear
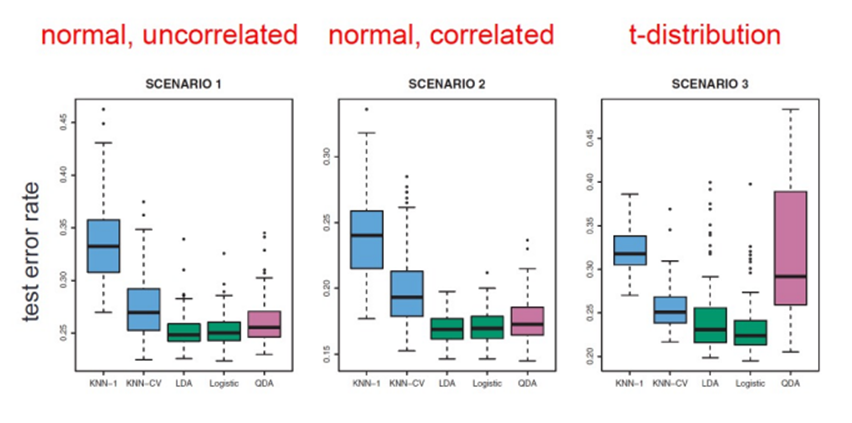
02. Non-Linear

