주어진 데이터로부터 미지의 값을 예측할 때, 의도에 맞게 잘 예측했는지 알기 위해서는 평가지표가 있어야 합니다. 즉, 평가의 기준이 있어야 하는 것인데, 분류작업에서는 대표적으로 모델이 얼마나 정확한 분류를 했는지 + 얼마나 정밀한지 + 실용적인 분류를 해냈는지에 대해 평가를 수행합니다. 이러한 내용을 모두 포함하는 것이 confusion matrix입니다.
1. Confusion Matrix
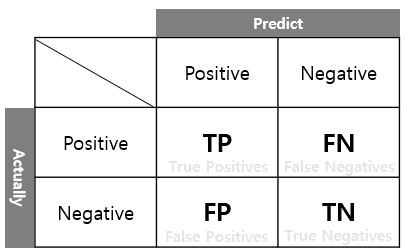
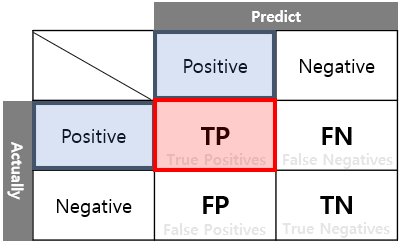
이진 분류를 한다고 가정해보겠습니다. 주어진 데이터를 Positive, Negative로 분류한다고 할 때 우리의 관심 범주는 Positive라고 하겠습니다. 그렇다면 모델을 통해 분류된 결과를 아래와 같이 4가지 정보로 나눌 수 있습니다.
(Positive = P / Negative = N 이라고 간단히 표현하겠습니다.)
TP(True Positives): 실제로 P인데, P로 분류된 경우입니다. 우리의 관심 범주를 정확하게 분류한 값.
FN(False Negatives): 실제로 P인데, N으로 분류한 경우입니다. 관심 범주를 관심 범주가 아니라고 잘못 분류한 값.
FP(False Positive): 실제로 N인데, P로 분류한 경우입니다. 관심 번주가 아닌데 관심 범주라고 잘못 분류한 값.
TN(True Negative): 실제로 N이고, N으로 분류한 경우입니다. 관심 범주가 아닌 것을 정확하게 분류한 값.
이 4가지 정보를 바탕으로, 3가지의 평가 척도를 얻을 수 있습니다.
1. 정확도(Accuracy)
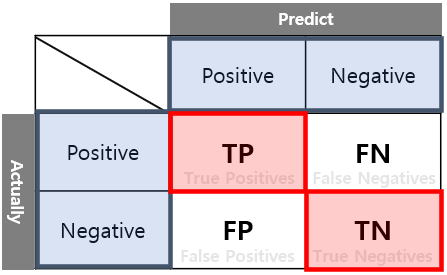
정확도(Accuracy)는 P를 P로, N을 N으로 정확하게 분류해낸 것을 말합니다. 즉, 모델이 얼마나 정확한지를 평가하는 척도입니다. 이 값이 높을수록 예측 정확도가 높다고 할 수 있습니다. 그리고 이 값으로부터 에러율을 구할 수 있는데,
Error Rate = 1 - Accuracy 로 나타낼 수 있습니다.
하지만 정확도만으로 모델을 평가하는 것은 편향에 빠질 수 있습니다. 예를 들어, 긍정인 것은 예측을 잘 했으나 부정적인 것들에 대해 예측을 잘하지 못했다면, 정확도는 잘 도출되었더라도 부정적인 것은 예측을 잘 못하기 때문에 좋은 모델이라고 할 수 없기 때문이죠. 이를 해결하기 위한 지표가 F1-Score입니다.
2. 정밀도(Precision)
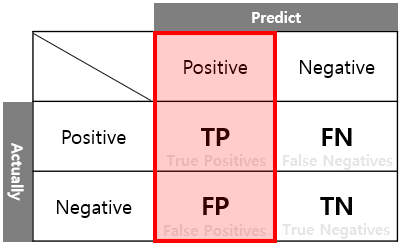
정밀도(Precision)는 주어진 데이터를 모델이 P라고 분류한 것들을 보고, 모델이 얼마나 믿을만한 정도로 분류했는지 평가하는 척도입니다. 즉, 예측한 값들 중에서 얼마나 잘 예측했는지를 나타내는 척도이죠.
3. 재현도(Recall)
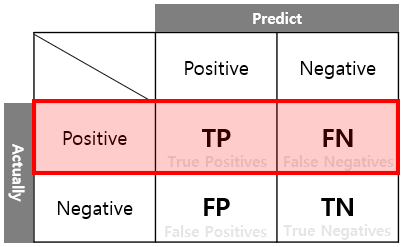
재현도(Recall)는 전체 예측 중에 P를 P라고 예측한 TP가 얼마나 많은가에 관한 것입니다. 관심 영역만을 얼마나 잘 추출했는지 의미합니다. 모형의 실용성과 관련된 척도입니다.
또한, 정밀도와 재현도를 통해 F1-Score를 구할 수 있습니다.
4. F1-Score

F1-Score는 보통 불균형한 데이터 분포에서의 분류문제에 평가척도로 사용됩니다. F1은 정밀도와 재현도를 이용해 조화평균을 구하여 평가 척도를 구성했기 때문에, 불균형 데이터일지라도 값의 크기 차이가 어느정도 상쇄되므로 데이터 분류 클래스의 분포가 균일하지 못할 때 많이 사용됩니다.
5. 민감도, 특이도
더 나아가서, 민감도와 특이도에 대해 알아보겠습니다. 민감도와 특이도는 크게 다르지 않습니다.
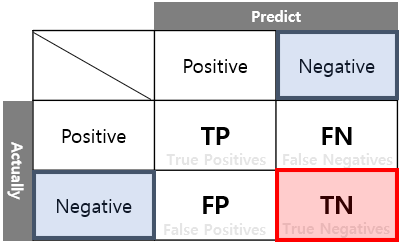
민감도(Sensitivity)는 재현도와 동일합니다. 실제 P를 P라고 예측한 비율이므로 민감도가 높을수록 좋은 척도라고 할 수 있습니다. 민감도는 맞은 것을 맞았다고 잘 예측한 수치 True Positive Rate(TPR)를 나타낼 수도 있습니다.
특이도(Specificity)는 민감도와 정 반대의 개념입니다. 즉, 우리의 관심영역이 아닌 부분의 민감도라고 생각할 수 있습니다. 특이도는 틀린 것을 틀렸다고 잘 예측한 수치 True Negative Rate(TNR)로 나타낼 수도 있습니다.

두 지표의 분포도를 그려 살펴보면, 중간에 Decision threshold 부분이 예측 값에 대한 cut off를 의미하고 기준이 되는 임계치를 나타냅니다. 이 임계치를 어떻게 설정하는지에 따라 민감도와 특이도의 값이 달라집니다.
분포도를 확인해보면 항상 환자를 예측하는 것, 비환자를 예측하는 것 사이에는 에러를 교집합으로 포함하고 있기 때문에 최적의 cutoff를 찾았다고 해도 어느정도의 오차는 포함할 수 밖에 없습니다. 또한, 임계점에 따라 살펴보면, TPR과 FPR은 비례관계이고 TNR과는 반비례 관계임을 알 수 있습니다.
2. ROC Curve + AUC

Confusion Matrix만으로 모델의 평가가 부족할 수 있어, 모델의 효율성을 평가하는 또다른 척도로 ROC Curve라는 것이 존재합니다.모델의 효율성을 민감도, 특이도를 이용해 그래프로 나타낸 것입니다.
ROC 커브와 x축이 이루고 있는 면적의 넓이를 AUC(Area Under Curve)라고 하며, x축 FDR(False Positive Rate)은 틀린 것을 맞았다고 잘못 예측한 수치이고, y축 TPR(True Positive Rate)은 맞은 것을 맞았다고 잘 예측한 수치를 나타냅니다. 이 커브 곡선으로부터 최적의 threshold를 찾을수도 있습니다.
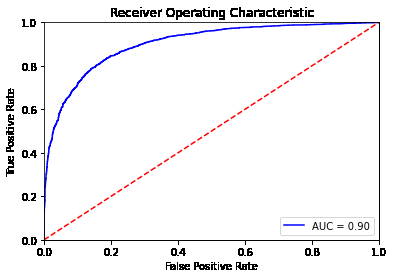
또한, 이 두 축 사이에 ROC 곡선은 FPR이 작은 상태에서 얼마나 큰 TPR을 얻을 수 있는지에 대해 의미하고, 면적이 1에 가까울수록 최적의 분류모델이 되겠죠. 다만, 아까 살펴본 TN, TP의 분포도에서 보았듯이 어느정도의 오차는 포함하기 때문에 1의 AUC를 가지긴 힘듭니다. 물론 두 분포가 겹치는 부분이 없다면 높은 AUC를 도출할 수 있을 것입니다.
요약하자면, 우리는 분류문제에서 무조건 정확도로만 모델의 성능이 좋고 나쁜지를 평가하는데에는 한계가 있습니다. 그래서 데이터마다의 클래스 분포, 상황에 따라서 다른 지표들과 함께 모델의 성능을 평가해야 합니다. 그 지표로 F1-Score와 ROC AUC를 통해 평가 척도를 검증하는 것입니다.
