Titanic - Machine Learning from Disaster (Pytorch)

이형래·2022년 3월 13일
PyTorchReLUadamkaggletitanic
0

DL

목록 보기
2/4

Kaggle Titanic 예제

kaggle을 처음 시작하며 대표예제인 Titanic 문제를 풀어보았습니다.

아직 입문이기에 EDA를 적용하거나 복잡한 모델을 구현하진 못하였고,
이론으로만 막연하게 이해하고있던 모델을
코드로 끝까지 구현하는데에 집중해서 데이터 전처리에 엄청난 편의성이 적용되었습니다.

Pytorch를 사용하여 2개의 FC hidden layer를 갖는 모델을 구현하였습니다.
각 hidden layer는 512개의 뉴런을 갖고, 다른 특징으로는 다음이 있습니다.

  • activation : ReLU
  • optimizer : Adam
  • learning rate : 0.01
  • loss function : CrossEntropyLoss
  • epochs : 500

Overview

주어진 문제는 타이타닉 승객들의 data를 학습하여,
test data에 있는 승객들의 생존 여부를 예측하는 모델을 만드는 것이 목표입니다.

주어진 train data는 다음과 같습니다.

ColumnDefinition
PassengerId승객 번호
Survived생존 여부
PclassTicket class (1:Upper, 2:Middle, 3:Lower)
Name승객 이름
Sex성
Age나이
SibSp배에 같이 탄 형제 및 배우자 수
Parch배에 같이 탄 부모 및 아이들 수
Ticket티켓 번호
Fare지불 요금
Cabin선실
Embarked승선한 항구(C:Cherbourg, Q:Queenstown, S=Southampton)

타이타닉 문제의 metric은 accruacy,
즉, 제대로 예측한 승객의 비율로 합니다.

1. Import Module

우선 필요한 모듈을 로딩합니다.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.preprocessing import StandardScaler

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader

2. Load dataset

traindata와 testdata를 각각
df_train과 df_test로 불러옵니다.

df_train = pd.read_csv('/kaggle/input/titanic/train.csv')
df_test = pd.read_csv('/kaggle/input/titanic/test.csv')

우선 data가 어떻게 생겼는지 확인을 해야합니다.

df_train.info()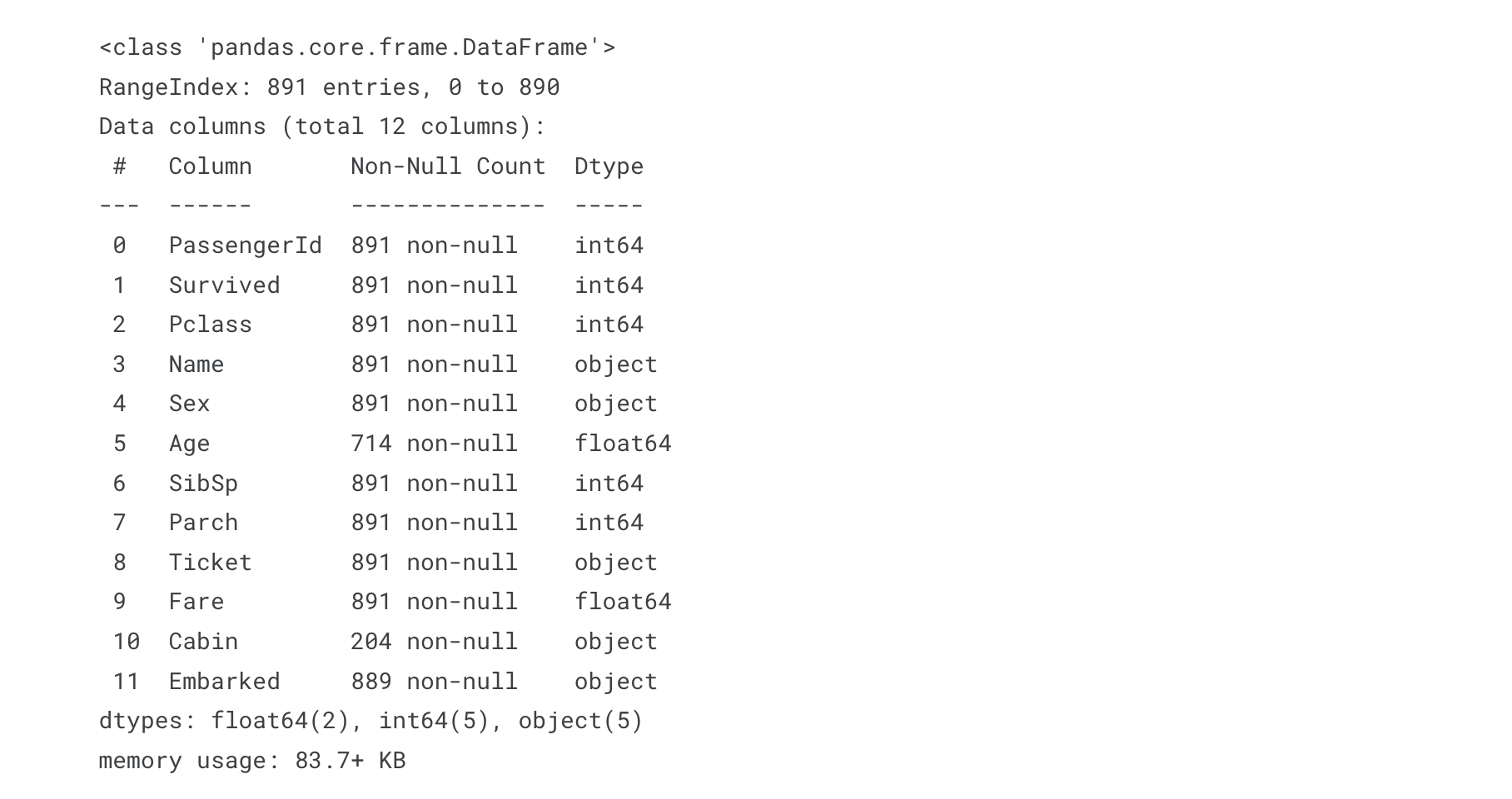

train data는 Age, Cabin, Embarked column에 결측값이 있고,
특히 Cabin은 204개로 전체 data에 비해 매우 적은 data만 존재함을 알 수 있습니다.

df_train.head()

df_test.info()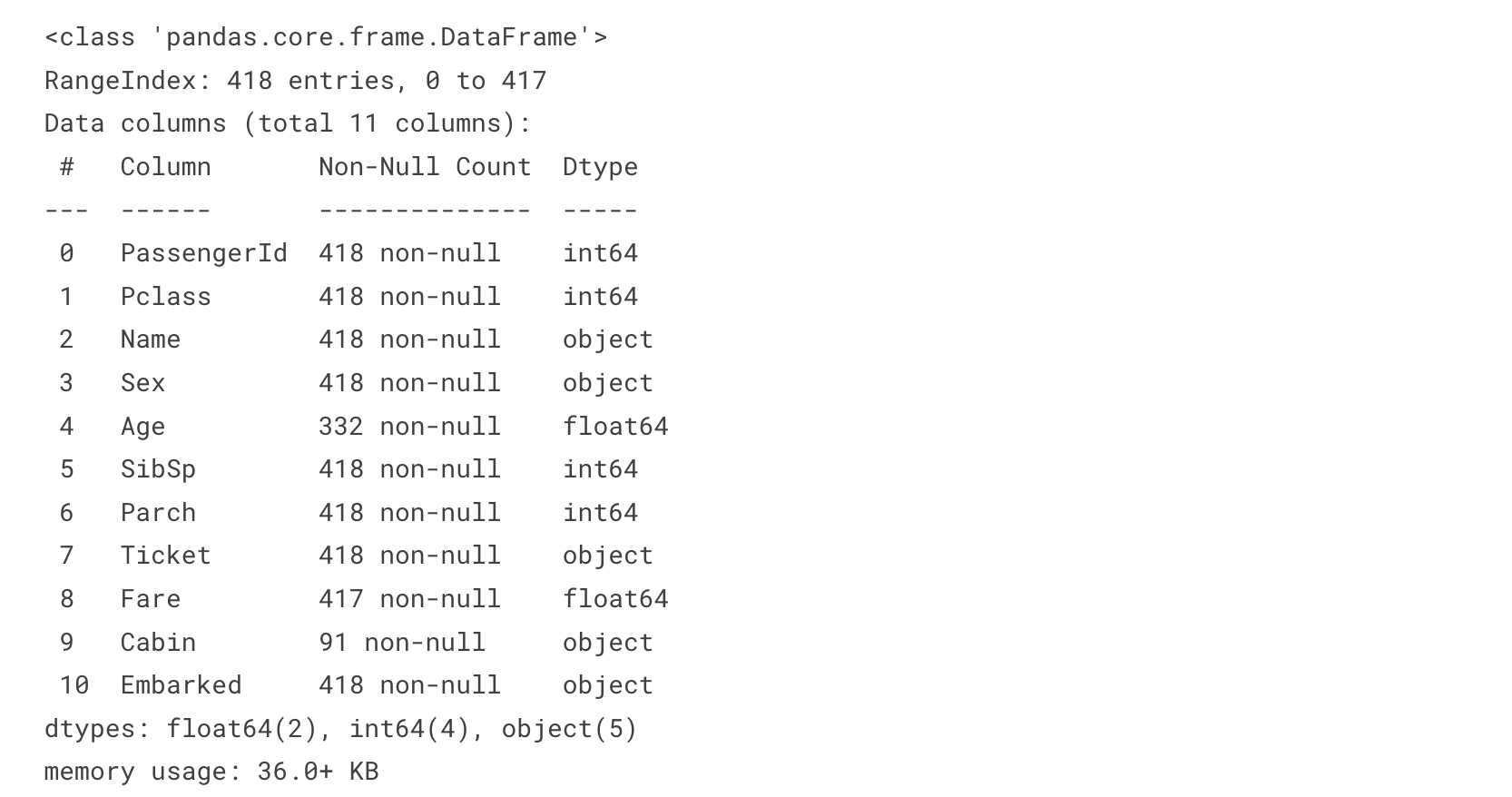

test data도 유사한 분포를 가지고 있음을 알 수 있습니다.
test data에는 label에 해당하는 Survived column이 없습니다.

df_test.head()

3. Data pre-processing

3.1 불필요한 data 삭제

우선 data에서 Name, Ticket, Cabin column을 삭제해줍니다.
Name, Ticket column은 생존 여부와 크게 연관이 없을것으로 보입니다.
하지만 Cabin은 영향을 끼칠 수 있습니다.
우선 위에 설명한대로 학습과정의 편의를 위해 많은 결측값을 갖고 있는 Cabin열도 삭제 해주었습니다.

df_train.drop(['Name','Ticket','Cabin'], axis=1, inplace=True)
df_test.drop(['Name','Ticket','Cabin'], axis=1, inplace=True)
# inplace=True는 원본 데이터를 수정하겠다는것을 의미.

3.2 object type의 column을 numerical한 type으로 변경

그 후, Sex, Embarked column의 값을 get_dummies메소드를 이용해 one-hot encoding을 해주었습니다.
학습을 위해 numerical한 data가 필요하고,
해당 column은 one-hot encoding으로 처리해줌이 적절해 보입니다.

neumerical data가 필요하다고 해서
female=1, male=2 식으로 정수형으로만 변경하면,
male = female * 2 같은 상관관계가 생겨버립니다.
실제로는 이런 관계가 존재하지 않으므로 one-hot encoding을 통해 처리합니다.

sex = pd.get_dummies(df_train['Sex'], drop_first=True)
embark = pd.get_dummies(df_train['Embarked'], drop_first=True)
# drop_first=True 는 첫번째 옵션을 drop함을 뜻합니다.
# 예로 Sex column에서 female이 1이라면, 0인 row는 자동으로 male을 의미하게 됩니다.
df_train = pd.concat([df_train, sex, embark], axis=1)
df_train.drop(['Sex', 'Embarked'], axis=1, inplace=True)

test data에 대해서도 동일한 과정을 거칩니다.

sex = pd.get_dummies(df_test['Sex'], drop_first=True)
embark = pd.get_dummies(df_test['Embarked'], drop_first=True)
df_test = pd.concat([df_test, sex, embark], axis=1)
df_test.drop(['Sex', 'Embarked'], axis=1, inplace=True)

3.3 결측값 처리

각 data의 평균값으로 Nan값을 채워주었습니다.

df_train.fillna(df_train.mean(), inplace=True)
df_test.fillna(df_test.mean(), inplace=True)

3.4 Scaler

원본 데이터들은 데이터 고유의 특성과 분포가 있습니다.
하지만 이 데이터를 그대로 학습에 사용하면
크게 작용하는 feature와, 거의 영향을 미치지못하는 feature가 생깁니다.
또한 패턴을 찾기 어려워지기때문에 학습이 느려지고 성능이 떨어집니다.
물론 정밀한 data 분석을 통해 어느정도 무게차이를 주는것은 중요하지만,
우선 편의를 위해 StandardScaler를 사용하여 data를 scaling하였습니다.

StandardScaler

  • 기존 변수의 범위를 정규 분포로 변환.
  • 모든 피처의 평균을 0, 분산을 1로 변환.
  • 이상치가 있다면 평균과 표준편차에 영향을 미치기 때문에 데이터의 확산이 달라지게 되므로 이상치가 많을때에는 사용하지 않는게 좋음.

우선 scaling 하기 전, lable과 PassengerId를 따로 빼두고 진행하였습니다.

y_train = df_train['Survived'].values
sub_PassengerId = df_test['PassengerId'].values

Scaler1 = StandardScaler()
Scaler2 = StandardScaler()

train_columns = df_train.columns
test_columns = df_test.columns

df_train = pd.DataFrame(Scaler1.fit_transform(df_train))
df_test = pd.DataFrame(Scaler2.fit_transform(df_test))
df_train.head()

df_train.columns = train_columns
df_test.columns = test_columns

X_train = df_train.iloc[:,2:].values

4. Set Model

4.1 modeling

모델은 512개의 뉴런을 갖는 2개의 fc hidden layer와,
마지막으로 2개 뉴런의 output을 갖는 output layer로 구성하였습니다.
각 hidden layer는 activation으로 ReLU를 사용하며,
overfitting을 방지하기 위해 Dropout을 적용합니다.

class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.layer1 = nn.Sequential(
        nn.Linear(8, 512),
        nn.ReLU(),
        nn.Dropout(0.2))
        self.layer2 = nn.Sequential(
        nn.Linear(512, 512),
        nn.ReLU(),
        nn.Dropout(0.2))
        self.layer3 = nn.Linear(512, 2)
        
    def forward(self, x):
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        return x
        
model = Net()
print(model)
>> Net(
	(layer1): Sequential(
	  (0): Linear(in_features=8, out_features=512, bias=True)
	  (1): ReLU()
	  (2): Dropout(p=0.2, inplace=False)
    )
    (layer2): Sequential(
      (0): Linear(in_features=512, out_features=512, bias=True)
      (1): ReLU()
      (2): Dropout(p=0.2, inplace=False)
    )
    (layer3): Linear(in_features=512, out_features=2, bias=True)
    )

4.2 dataset & dataloader

data를 좀 더 쉽게 다룰 수 있도록 Dataset, DataLoader를 사용하였습니다.

X_train, y_train으로 dataset을 만들면
이 dataset으로 dataloader를 사용할 수 있습니다.
minibatch크기는 64로,
그리고 shuffle=True를 해줍니다.

shuffle=True를 해 준 이유는
각 epoch마다 dataset을 섞어서 data가 학습되는 순서를 바꾸기 위함입니다.
이는 모델이 dataset의 순서에 익숙해지는것을 방지합니다.

또한, DataLoader의 옵션 중 drop_last는 설정하지 않았는데,
학습 data의 수는 891개이고, batch_size는 64이므로
14개의 배치를 갖고, 마지막 배치의 크기는 59이므로 크게 영향이 없다고 판단하였습니다.

X_train = torch.FloatTensor(X_train)
y_train = torch.FloatTensor(y_train)

dataset = TensorDataset(X_train, y_train)
dataloader = DataLoader(dataset, batch_size=64, shuffle=True)

4.3 loss functoin & optimizer

loss function은 CrossEntropyLoss를 사용합니다.
이때, torch에서 제공하는 CrossEntropyLoss함수는 softmax함수를 포함합니다.
따라서 model의 마지막 layer가 softmax일 필요는 없습니다.

optimizer로는 Adam을 사용합니다.
learning rate은 0.01로 설정하였습니다.

criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

5. Training

총 epoch는 500회를 거치고,
loss가 minimum값을 가질때마다 그때의 state를 저장합니다.

nb_epochs = 500
train_loss_min = np.Inf
for epoch in range(nb_epochs):
    num_right = 0
    train_loss = 0
    for batch_idx, samples in enumerate(dataloader):
        x_train, y_train = samples
        
        prediction = model(x_train)
        loss = criterion(prediction, y_train.long())
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        labels = torch.argmax(prediction, dim=1)
        num_right += torch.sum(labels == y_train)
        train_loss += loss.item() * len(x_train)

#         print('Epoch {}/{}, Batch {}/{}'.format(epoch, nb_epochs, batch_idx, len(dataloader)))
        
    train_loss = train_loss / len(X_train)
    if (epoch + 1) % 20 == 0:
        print('Epoch {}/{}, Prediction : {}/{}, Cost : {}'.format(epoch+1, nb_epochs, num_right, len(X_train), train_loss))
    if train_loss <= train_loss_min:
        print('=*=*=*= Loss decreased ({:6f} ===> {:6f}). Saving the model! =*=*=*='.format(train_loss_min, train_loss))
        torch.save(model.state_dict(), 'model.pt')
        train_loss_min = train_loss
        
print('Training Ended!')
>>
=*=*=*= Loss decreased (   inf ===> 0.724241). Saving the model! =*=*=*=
=*=*=*= Loss decreased (0.724241 ===> 0.437275). Saving the model! =*=*=*=
=*=*=*= Loss decreased (0.437275 ===> 0.421594). Saving the model! =*=*=*=
=*=*=*= Loss decreased (0.421594 ===> 0.416404). Saving the model! =*=*=*=
=*=*=*= Loss decreased (0.416404 ===> 0.416275). Saving the model! =*=*=*=
=*=*=*= Loss decreased (0.416275 ===> 0.404020). Saving the model! =*=*=*=
=*=*=*= Loss decreased (0.404020 ===> 0.387413). Saving the model! =*=*=*=
=*=*=*= Loss decreased (0.387413 ===> 0.378550). Saving the model! =*=*=*=
=*=*=*= Loss decreased (0.378550 ===> 0.370775). Saving the model! =*=*=*=
Epoch 20/500, Prediction : 745/891, Cost : 0.37458394727054

.....

=*=*=*= Loss decreased (0.246306 ===> 0.240609). Saving the model! =*=*=*=
Epoch 460/500, Prediction : 790/891, Cost : 0.25907919928013406
Epoch 480/500, Prediction : 792/891, Cost : 0.26102976599660116
Epoch 500/500, Prediction : 793/891, Cost : 0.2627205300143806
Training Ended!

loss가 0.240609일때 minimun값을 가지고 저장되었습니다.

6. Prediction

train하는과정이 아니기 때문에 gradient를 구할 필요가 없으므로
with torch.no_grad()를 통해 자동으로 gradient를 트래킹하지 않게 설정합니다.

X_test = torch.FloatTensor(df_test.iloc[:,1:].values)
with torch.no_grad():
    result = model(X_test)
labels = torch.argmax(result, dim=1)
survived = labels.numpy()

7. Submission

submission = pd.DataFrame({'PassengerId': sub_PassengerId, 'Survived': survived})
submission.to_csv('submission.csv', index=False)

결과

public score 0.74정도밖에 미치지 못한 모델이지만,
직접 모델을 구현해본 경험에 의미를 두고 학습을 이어가야겠다.
다음에는 EDA를 적용해 data를 잘 가공하고,
추가로 ensemble modeling과 reguralization 기법들을 추가하여
accuracy를 더 키울 수 있는 모델을 구현해봐야겠다.

profile
이형래
머신러닝을 공부하고 있습니다. 특히 비전 분야에 관심이 많습니다.
이전 포스트

GoogleColab에서 Kaggle데이터 바로 사용하는 방법

다음 포스트

Titanic with EDA

0개의 댓글