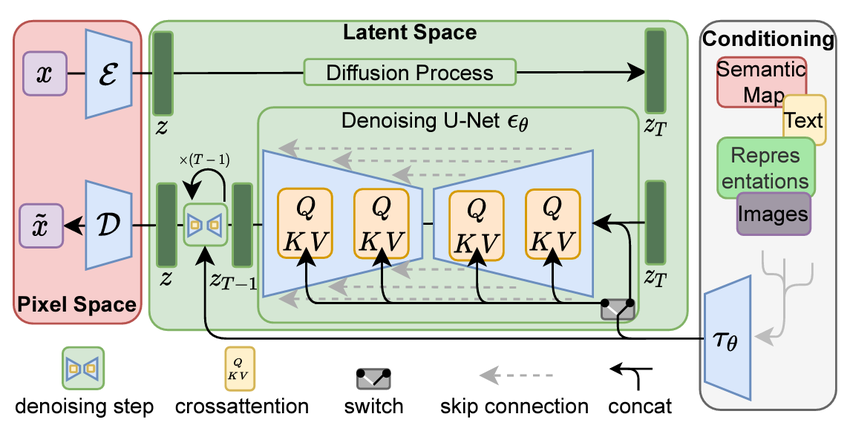
3번째 논문 요약 시리즈는 DDPM 이라고 불리는 Diffusion Model이다.

최근 Sora나 Stable Diffusion Model 같이 생성형 모델이 점점 늘어나고 있다.
Text-to-Image 모델로 직접 봐보니 퀄리티도 상당하고 Diffusion model, Transformer 같은 기존에 발표되었던 모델들을 더 발전시켜나가는 속도가 정말 대단한 것 같다.
이번 논문도 약 1달 전에 읽었지만, 읽었다는 것을 잊고 있다가 최근에 Sora와 Stable Diffusion의 등장으로 생각이 나서 다시 읽고 요약을 하게되었다.

참고

[논문 출처] https://arxiv.org/abs/2006.11239

[Github site] https://github.com/lucidrains/denoising-diffusion-pytorch

---

Stable Diffusion3 - stability.ai


Sora - OpenAI

Introduction

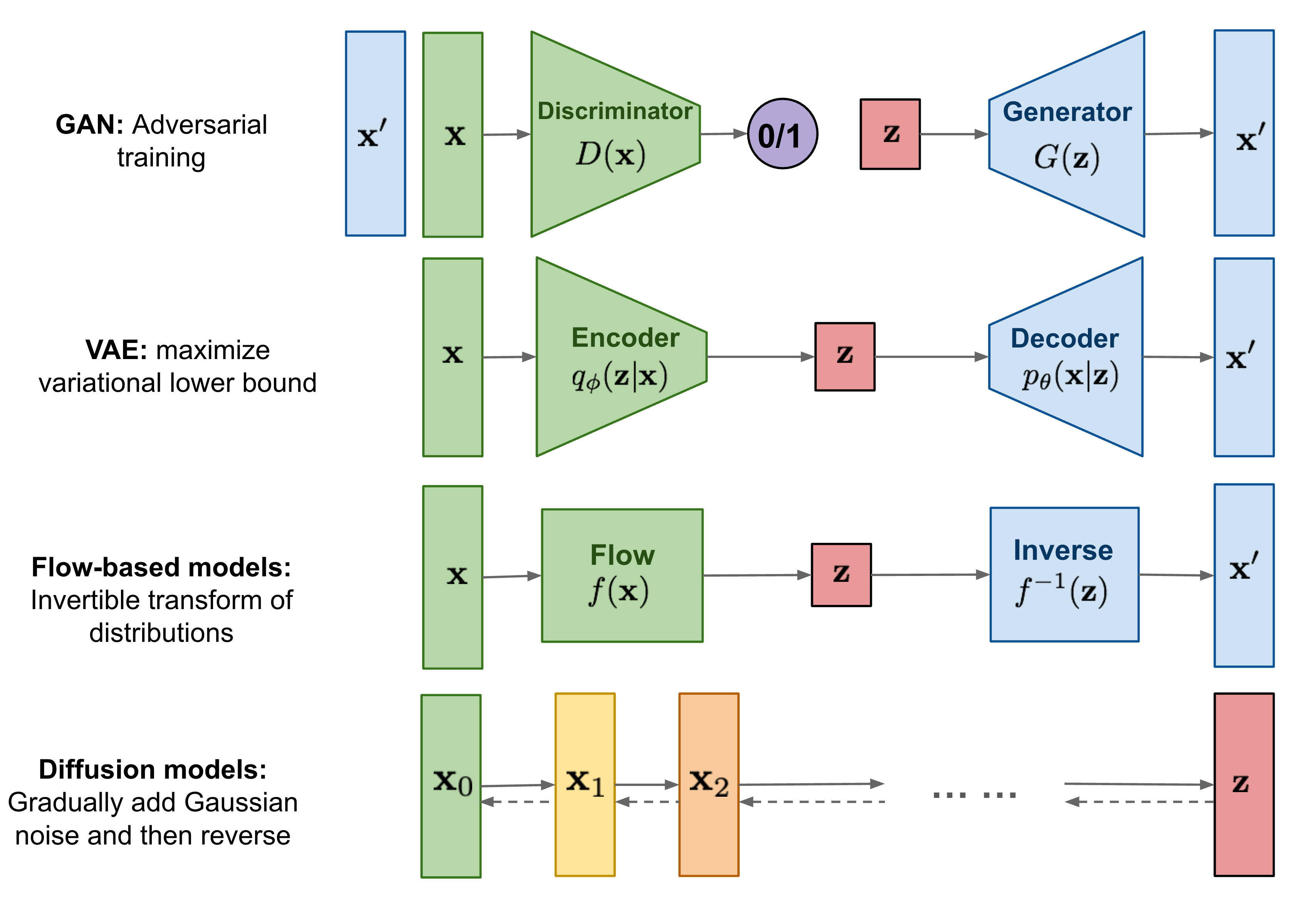
DDPM 이전에 GAN과 VAE가 있었는데 이 둘은 이미지와 오디오 샘플들을 합치는 것이 주 목적이였다. 그에 비해 DDPM은 image에 noise를 더해가면서 이 noise가 주어졌을 때 어떻게 원본 이미지를 복구할 것인가에 대한 문제이다.

Diffusion Probabilistic Model은 parameter화된 Markov chain을 사용한다. 여기서 Markov chain이란 특정 상태의 확률 (t+1 일 때)은 오직 현재 (t 일 때)의 상태에 의존한다는 의미로 이것이 Diffusion Model에 적용되면 signal이 없어지기 전까지 sample이미지의 반대 방향으로 noise를 더해가면서 학습해나가는 것을 의미한다.

Transitions of this chain are learned to reverse a diffusion process, which is Markov chain that gradually adds noise to the data in the opposite direction of sampling until signal is destroyed.

Diffusion model은 정의하기가 직관적이고 훈련시키기에 효율적이지만, high quality의 sample을 만들기 힘들다는 단점이 있다. 그래서 연구원들은 이 논문을 통해 Diffusion model도 high quality의 image를 생성할 수 있다는 것을 보이고자 한다.
또한 Diffusion model의 특정한 매개변수화가 훈련시키는 도중 여러 noise 수준에 대한 denoising score와 sampling 중 훈련된 Langevin 역학과 동일하다는 것을 보인다.

In addition, We show that a certain parameterization of diffusion models reveals an equivalence with denoising score matching over multiple noise levels during training and with annealed Langevin dynamics during sampling.

사실 이 말을 읽고 이해해보려고 했는데 Langevin 역학이 뭔지도 모르고 이 parameterization을 통해 최고의 결과를 얻었다고 주장하기 때문에 앞으로 이 말이 무슨 의미인지도 함께 알아보고자 한다.

Background

Diffusion model은 latent variable model (hidden variable)이다.

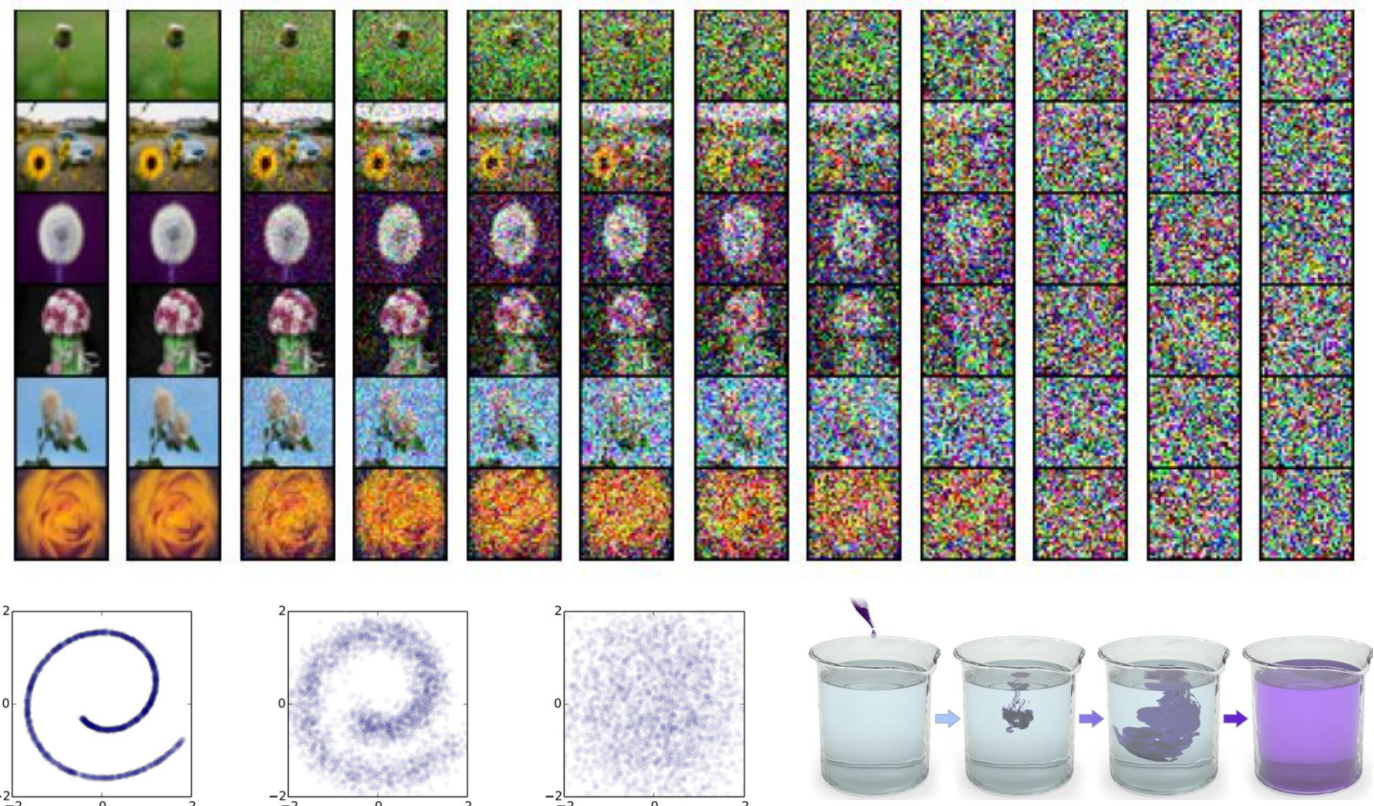
Diffusion이라는 단어에서 유추할 수 있듯이 어떤 것이 퍼지는 현상이 이미지에 적용되었다고 생각하면 되는데, 여기서 "어떤 것"이 Noise라고 이해하면 편하다. 위의 그림에서 왼쪽에서 오른쪽 방향으로 Noise를 더해가면서 해상도가 점점 흐려지는 이미지가 되는 것을 확인할 수 있다.

1. Forward (Diffusion) process

$q(x_{1:T}|x_0)=\Pi_{t=1}^Tq(x_t|q_{t-1}),~~~q(x_t|x_{t-1}):={N}(x_t;\sqrt{1-\beta_t}~x_{t-1},~\beta_tI)$

Markov chain으로 data에 noise를 더해가는 과정으로 variance scheduling $\beta_1,,,\beta_T$로 scaling을 한 뒤 점차적으로 Gaussian Noise를 더해나간다.
여기서 Noise schedule을 하게 되면 이미지의 평균은 0에 근접하도록 하고 분산은 1에 근접하도록 하는 것이다.

수식에 대해 몇가지 설명을 하면,

• $\beta_t=1$이면 $\sqrt{1-\beta_t}~x_{t-1}=0$이 되므로 이전 정보 없이 Noise만 증가하게 된다.

• $\sqrt{1-\beta_t}$가 붙은 이유는 variance scheduling으로 발산하는 것을 방지하기 위함이다.

• $q(x_t|x_{t-1})$ : 이전 단계에 Noise를 추가해 현재의 이미지를 만드는 과정

• $x_T$ : Noise로 인하여 이미지가 destroy된 단계

2. Reverse process

$p_\theta (x_{0:T}) :=p(x_T)\Pi_{t=1}^Tp_{\theta}(x_{t-1}|x_t),~~~~p_\theta(x_{t-1}|x_t):=N(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t)$

VAE에서의 decoding 과정과 유사한데 Reverse process의 주 목적은 $x_t$를 보고 $x_{t-1}$의 평균 $\mu_\theta$과 분산 $\Sigma_\theta$를 예측하는 것이다.

3. Loss function

$E[-log p_\theta(x_0)]~\le~E_q[-log{{p_\theta (x_{0:T})}\over{q(x_{1:T}|x_0)}}]=E_q[-log p(x_T)-\sum_{t\ge 1}log{{p_\theta (x_{t-1}|x_t)}\over{q(x_t|x_{t-1})}}]~=:~L$

이 논문에서는 negative log likelihood를 최소화 하는 방향으로 진행하고자 하는 것이고 정리를 하면 우항에 있는 ELBO term 처럼 된다.
이를 통해 L의 random term을 SGD (Stochastic Gradient Descent)로 최적화함으로써 효율적인 훈련이 가능해진다.

Efficient training is therefore possible by optimizing random terms of L with stochastic gradient descent. Further improvements come from variance reduction by rewriting L as:

$E_q[D_{KL}(q(x_T|x_0)||p(x_T))+\sum_{t\gt 1}D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))-log p_\theta(x_0|x_1)]$

$=E_q[L_T+\sum_{t>1}L_{t-1}-L_0]$

ELBO를 통해 두 분포 $P$와 $Q$의 차이를 최소화 하고자 KL Divergence를 사용했다.

$q(x_{t-1}|x_t,x_0)=N(x_{t-1};\hat{\mu_t}(x_t,x_0),\hat{\beta_t}I,\\~\\~~~~~~where ~~\hat{\mu_t}(x_t,x_0):={{\sqrt{\bar{\alpha}_{t-1}}\beta_t}\over{1-\bar{\alpha}_t}}x_0+{{\sqrt{\alpha}(1-\bar{\alpha}_{t-1})}\over{1-\bar{\alpha}_t}}~~and~~\hat{\beta}_t:={{1-\bar{\alpha}_{t-1}}\over{1-\bar{\alpha}_t}}\beta_t$

Diffusion models and denoising autoencoders

Diffusion model은 hidden variable의 제한된 부류인 것 처럼 보이지만, 실행에서는 높은 수의 자유도를 허용한다.

Diffusion models might appear to be a restricted class of latent variable models, but they allow a large number of degrees of freedom in implementation

Inductive bias를 늘려 더욱 더 stable하고 높은 성능을 나타낼 수 있었다.

$L_{t-1}=E_{x_0,\epsilon}[{1\over{2\sigma_t^2}}||{1\over{\sqrt{\alpha_t}}}(x_t(x_0,\epsilon)-{{\beta_t}\over{\sqrt{1-\bar{\alpha}_t}}}\epsilon-\mu_\theta(x_t(x_0,\epsilon),t)||^2]+C$

$L_{t-1}$을 식으로 표현하면 위와 같다.

이 식으로 알 수 있는 것은 $\mu_\theta$는 무조건 주어진 $x_t$에 대해 ${1\over{\sqrt{\alpha_t}}}(x_t-{\beta_t\over{\sqrt{1-\bar{\alpha}_t}}}\epsilon)$을 예측할 수 있어야 한다는 것이다.
여기서 parameterization을 선택할 수 있다.

$\mu_\theta(x_t,t)=\hat{\mu_t}(x_t,{1\over{\sqrt{\bar\alpha}}_t}(x_t-\sqrt{1-\bar{\alpha}_t}\epsilon_\theta(x_t)))={1\over{\sqrt{\alpha_t}}}(x_t-{\beta_t\over{\sqrt{1-\bar{\alpha_t}}}}\epsilon_\theta(x_t,t))$

여기서 맨 처음에 언급했던 Langevin dynamics에 대한 언급이 나온다. Algorithm2를 보면 $\epsilon_\theta$가 data의 density의 gradient를 학습함으로써 sampling 과정이 완료되는데 이 과정이 Langevin dynamics를 닮았다고 한다.

Optimizing an objective resembling denoising score matching is equivalent to using variational inference to fit the finite-time marginal of a sampling chain resembling Langevin dynamics

참고

Langevin Dynamics - WIKIPEDIA

Data Scaling

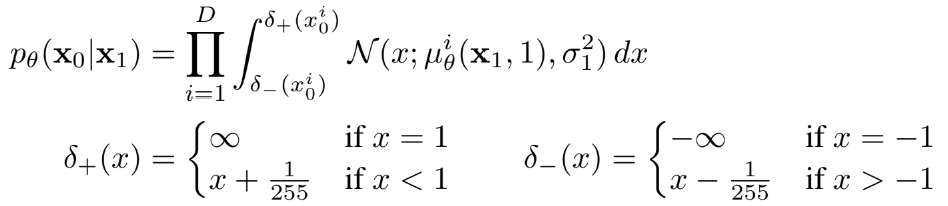
image data가 [0,255] 사이의 값을 갖도록 scaling을 하는데 이 과정을 통해 neural network의 reverse process가 $P(x_T)$에서 시작하는 scale 된 input만 처리하는 것을 보장해준다.

This ensures that the neural network reverse process operates on consistently scaled inputs starting from the standard normal prior $p(x_T)$.

Simplified training objective

$L_\text{simple}(\theta) := E_{t,x_0,\epsilon}[||\epsilon-\epsilon_\theta(\sqrt{\bar{\alpha_t}}x_0+\sqrt{1-\bar{\alpha_t}}\epsilon,t)||^2]$

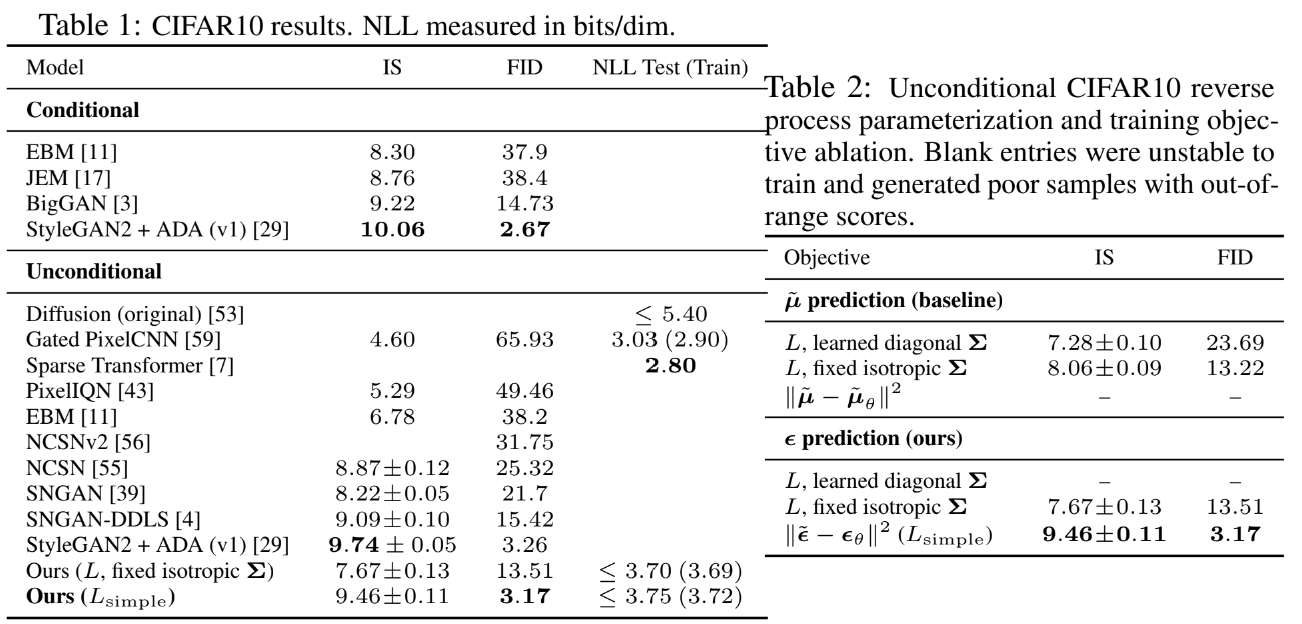
Experiment

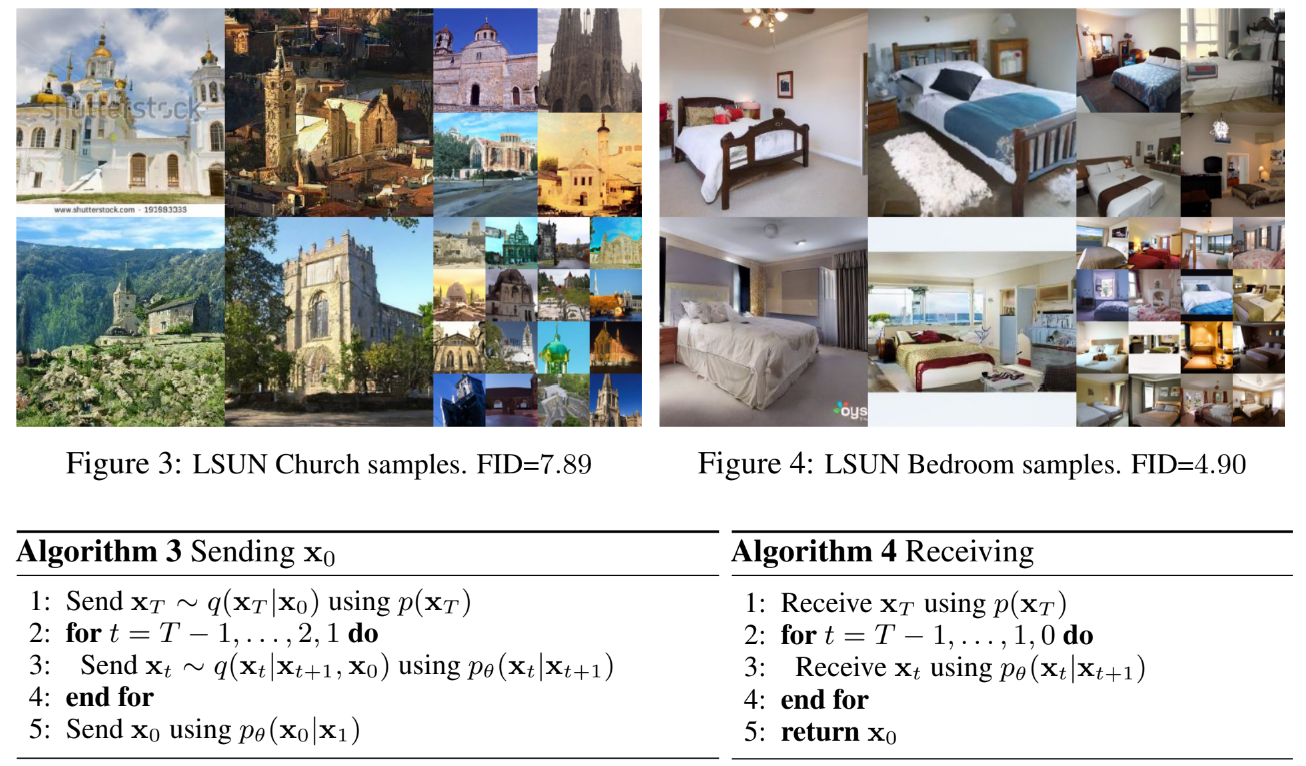
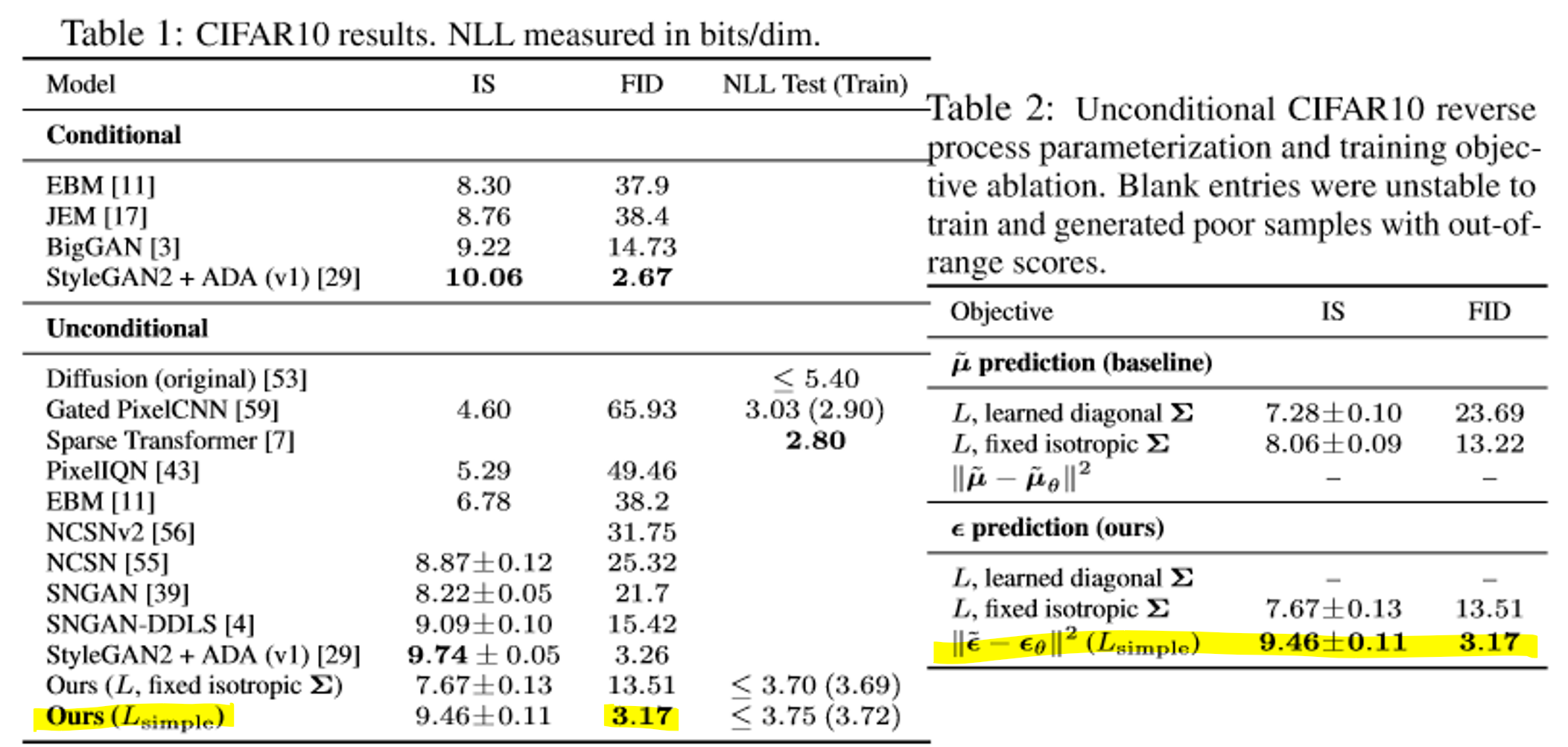
공부의 흔적...