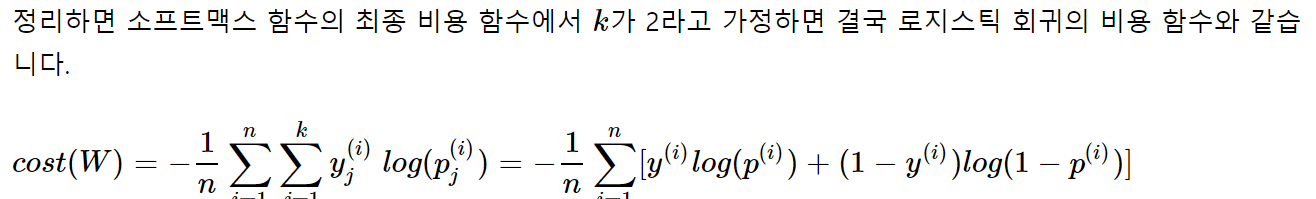1. Maximum Likelilhood Estimation (최대 가능도 추정)
1) Likelihood Function
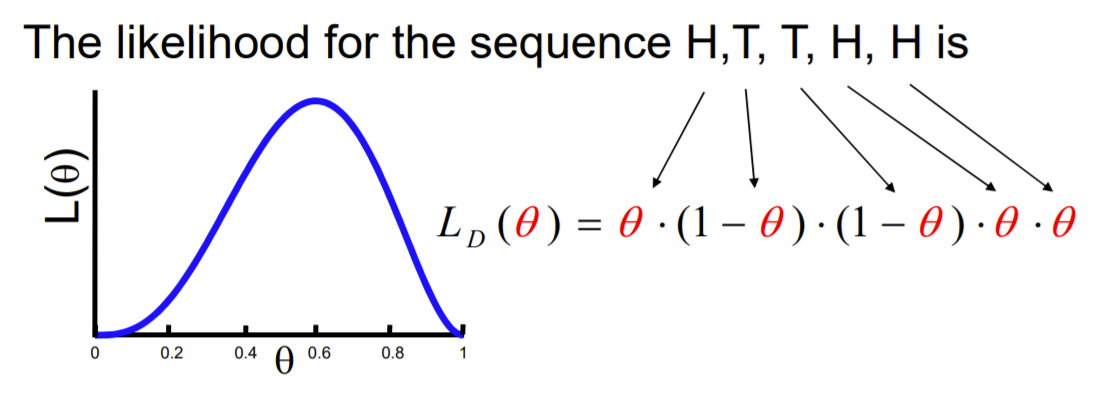
ex) 압정 던지기

넓은 면을 Head, 뾰족한 부분을 Tail이라 하자
-
그럼 각각 나올 확률은

-
그래서 현재 theta를 Head가 나올 확률로 정했으니까, 이 때 Head를 얼마나 자주 볼까에 대한 함수가 Likelyhood Function!
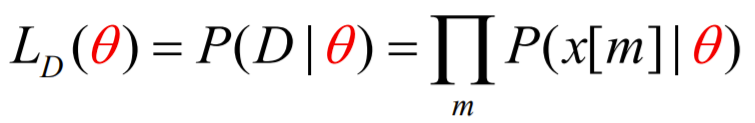
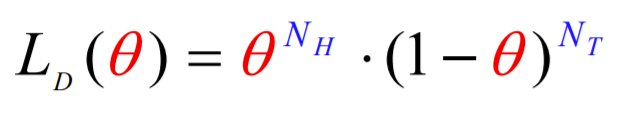
2) Maximum Likelihood Estimation
이름에서 알 수 있듯, 가장 나올 가능성이 높은 경우가 나올 확률을 만드는 theta를 찾는 거라서, likelihood function을 최대로 하는 parameter를 정하면, 그게 MLE가 되겠지?
-
우선 likelihood function에 log를 씌워
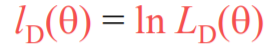
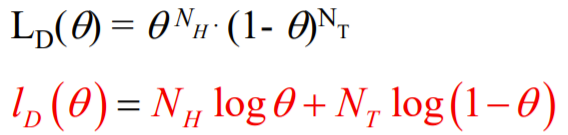
-
이걸 미분한게 0이 될 때 극값 갖겠지 ➡ 극댓값이 최댓값
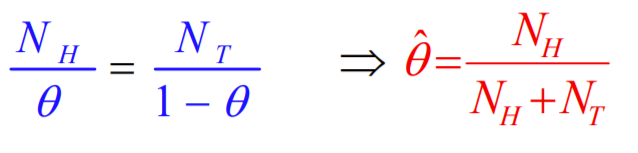
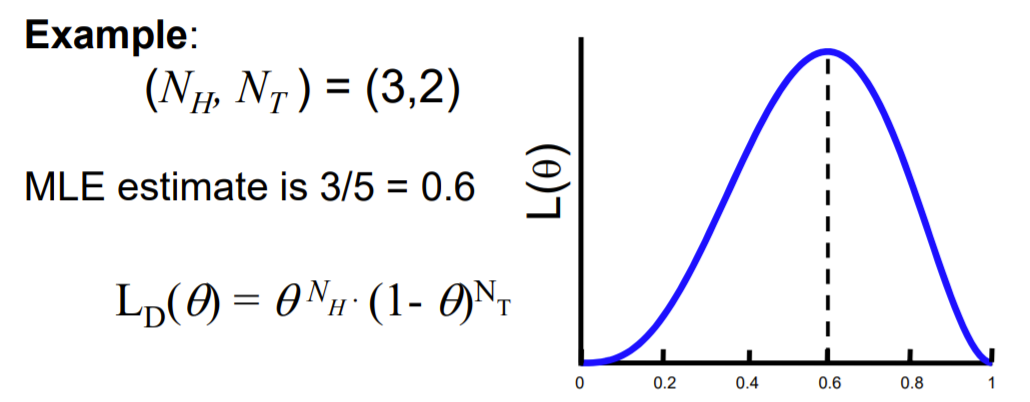
3) 파라미터(theta)가 2개이상일때 MLE
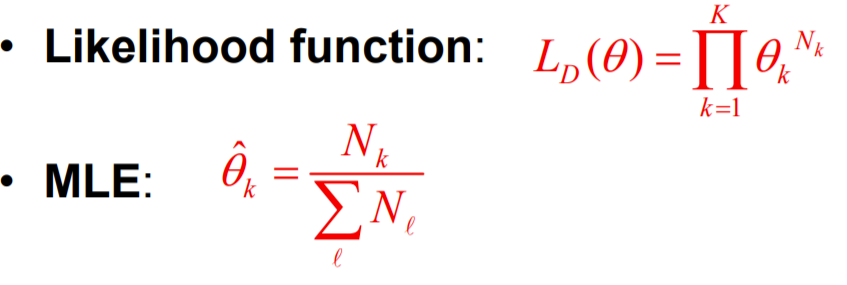
4) Odds와 Odds ratio
-
Odds
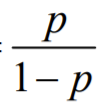
당신이 물고기를 잡을 확률(P) / 물고기를 한마리도 잡지 못할 확률(1-P)
잡을 확률이 물고기 잡지 못할 확률의 몇 배가 되는가?
이 비가 Odds ratio -
Log Odds
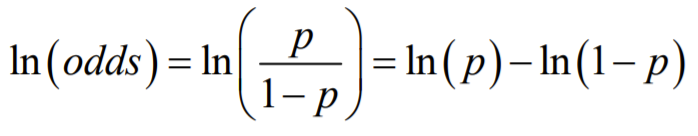
2. Logistic Regression
-
Logistic Function (= Sigmoid Function)
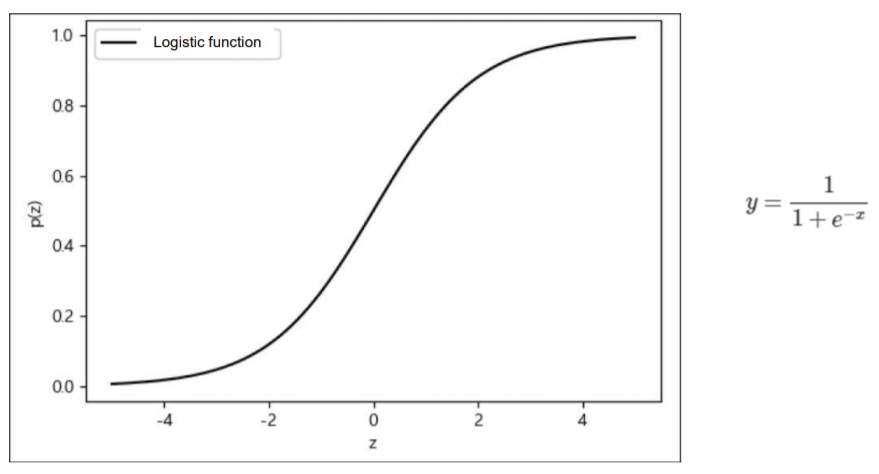
-
Linear Regression 한 값을 Logistic Function의 input으로 넣기
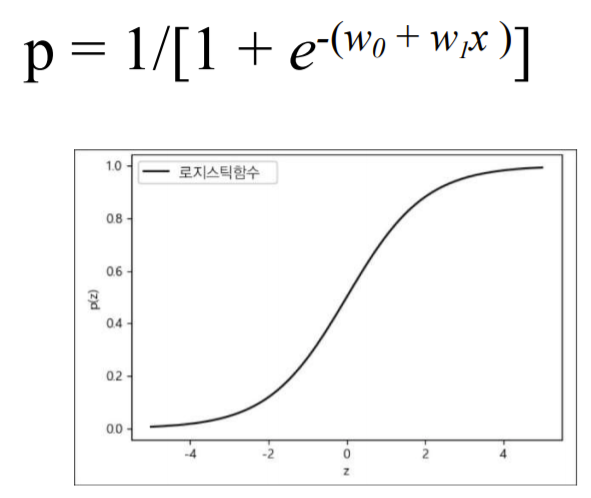
- 선형 회귀 값이 0이면, p = 1/2
- 선형 회귀 값이 무한히 커지면, p = 1
- 선형 회귀 값이 무한히 작아지면, p = 0
- Logistic Regression
0 또는 1로 결과값이 딱 나누어 떨어져야 하는 경우
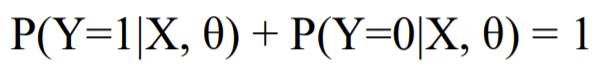
-
예측값
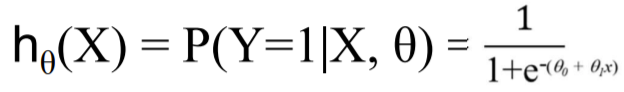
-
선형회귀와 비용함수를 구하는 과정은 같음
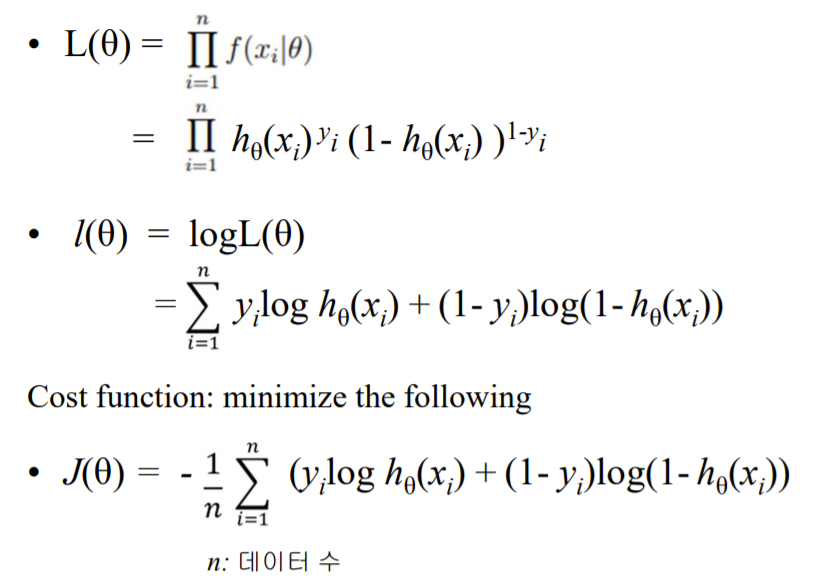
-
경사하강법

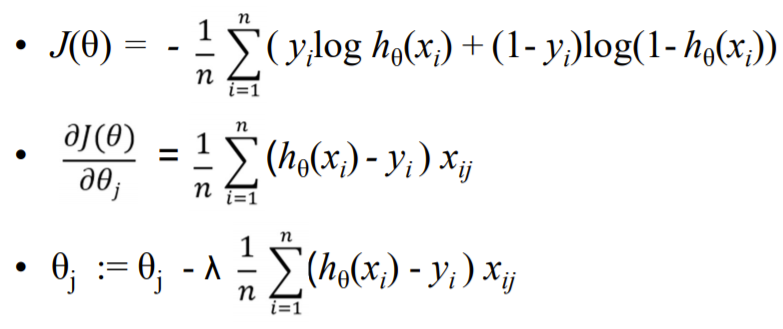
ex) 6이 input으로 들어왔을 때의 theta 예측하기
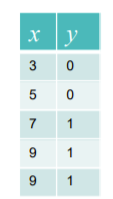
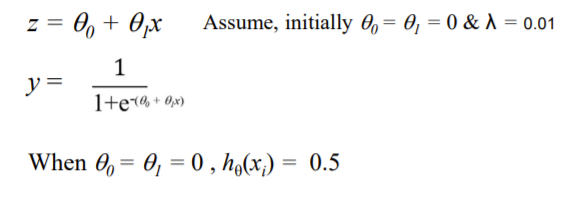
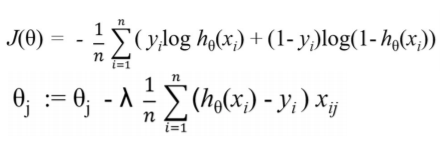
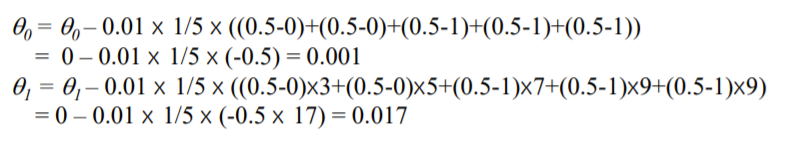
3. Softmax Regression
-
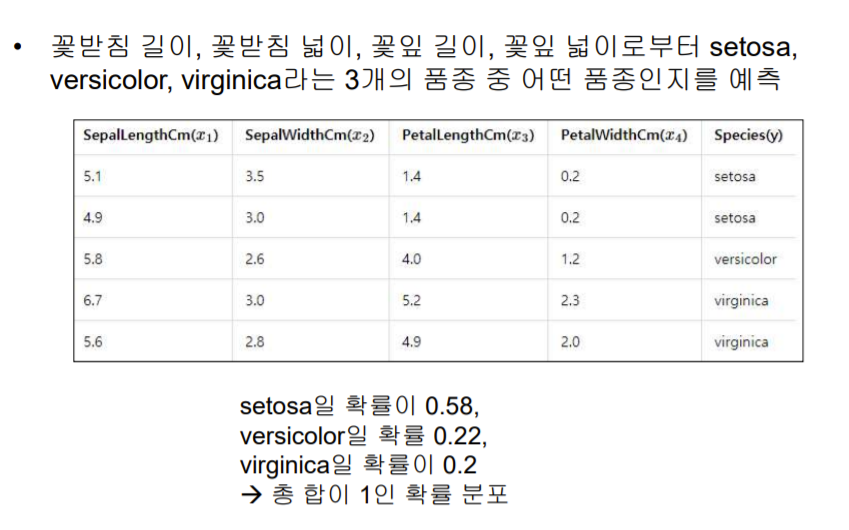
Logistic Regression처럼 0,1로 나누어 떨어지는 게 아니라, class가 여러개로 나누어 떨어지는 경우
✔ Multi-class Classification
-
Softmax Regression과 Logistic Regression 비교
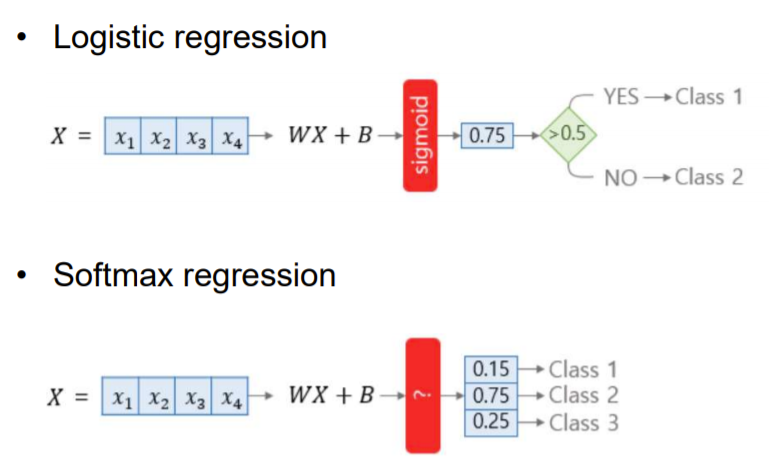
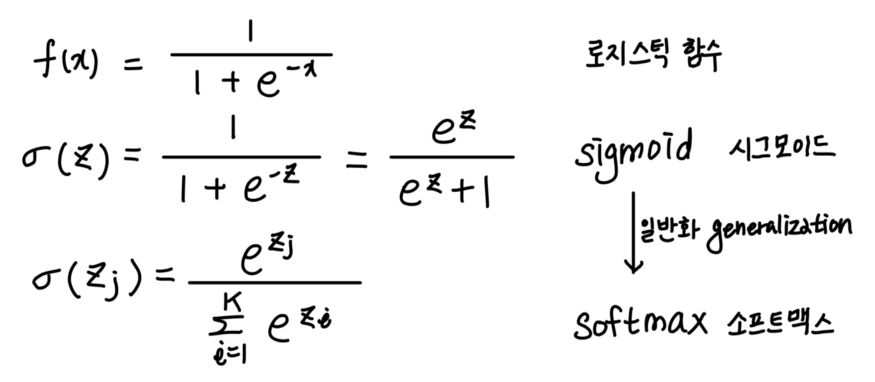
- 시그모이드가 로지스틱 함수의 일종이고, input이 여러개여도 사용가능하도록 일반화 한 것이 softmax
- Softmax 함수의 이해
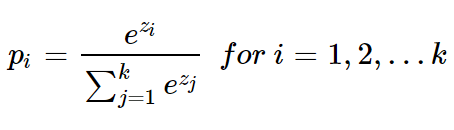
pi : i번째 클래스가 정답일 확률
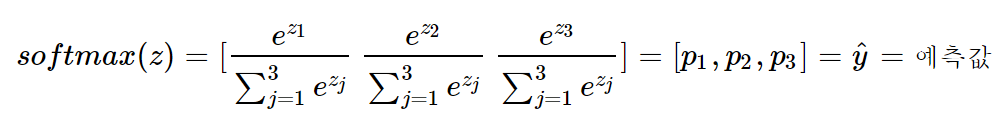
p1,p2,p3 각각은 1번 클래스가 정답일 확률, 2번 클래스가 정답일 확률, 3번 클래스가 정답일 확률을 나타내며 각각 0과 1사이의 값으로 총 합은 1이 됨
- Softmax 함수에 대한 궁금증
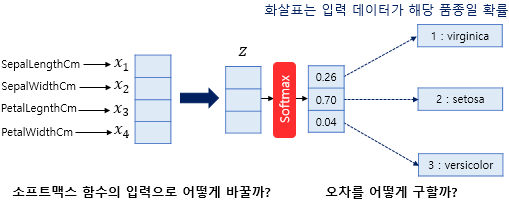
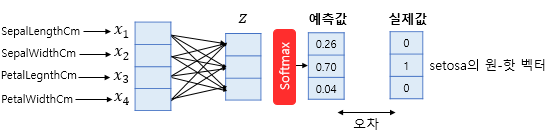
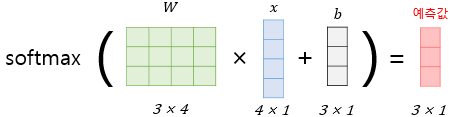
1) 소프트맥스 함수의 입력으로 어떻게 바꿀까?
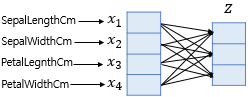
4차원 벡터를 입력으로 받아, 화살표마다 가중치를 다르게 주어, 3차원 벡터 z로 표현 (오차를 최소화하는 가중치)
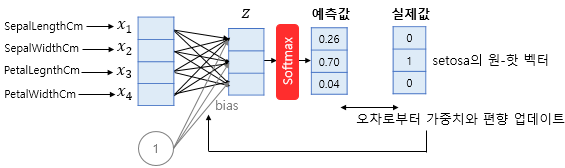
2) 오차를 어떻게 구할까?
- 실제 값을 원-핫으로 표현

- 손실함수
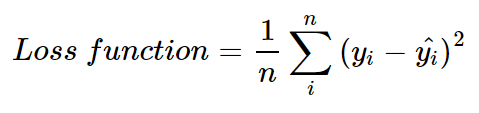
기댓값 말고 제곱오차만 살펴보면,
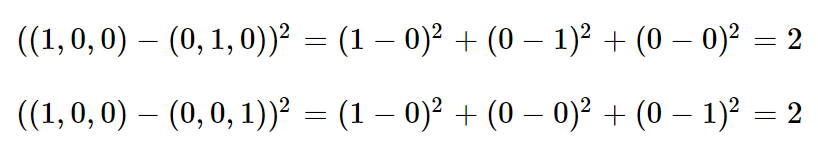
원핫 인코딩으로 했기 때문에, 모든 유클리드 거리가 동일
cf) 만약 정수 인코딩이라면, ex) 사과:1 바나나:2 파인애플:3 일 때
사과를 바나나라고 해서 틀렸든, 사과를 파인애플이라고 해서 틀렸든 의미에 큰 차이가 없음에도, (2-1)^2 = 1, (3-1)^2=4로 유클리드 거리에 차이가 있음
- 크로스 엔트로피 함수
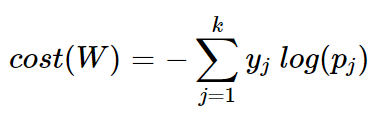
-
yj 는 실제값 원-핫 벡터의 j번째 인덱스를 의미하며, pj는 샘플 데이터가 j번째 클래스일 확률
-
pj=1 은 y를 정확하게 예측한 경우가 됨. 이를 식에 대입해보면 −1log(1)=0이 되기 때문에, 결과적으로 y를 정확하게 예측한 경우의 크로스 엔트로피 함수의 값은 0이됨.
-
즉, 이 크로스 엔트로피 함수를 최소화하는 방향으로 학습하면 됨
-
n개의 전체 데이터에 대해서 평균을 내보면, 최종 비용 함수는
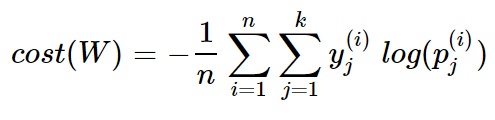
-
클래스가 2개일때 (이진분류일 때) 로지스틱 함수의 비용함수와 같아짐