unsupervised learning
비지도 학습; label 없이 훈련됨

그 중에서도, Clustering!
- Goal : unlabeled를 비슷하거끼리 묶기
- 사용 : 데이터 정리, 숨겨진 구조 찾을 때, 전처리
1. Flat 알고리즘
random하게 partitioning 시작해서 그것을 iterative하게 refine함 (K-means 클러스터링)
- Partitioning 알고리즘 (K개로 나누기)
- dataset이랑 K 주어지면
- globally optimal한 K 군집으로 묶기
- K-Means : 벡터의 무게중심 이용


-
처음에 좋은 seed를 고르는 것이 중요함
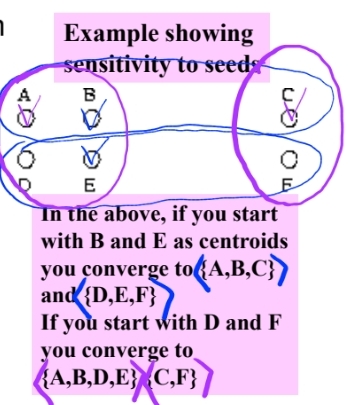
-
K-means ++
1) 맨 처음 c1을 랜덤하게 잡음
2) 가장 멀게 Cj를 잡음
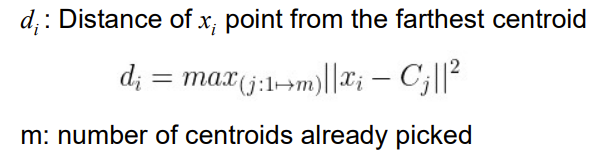
3) 반복
- 이전 점들과 멀리 떨어진 점들이 선택되다보면 자연스레 서로 떨어진 점들이 선택될 것
- 몇 개의 군집으로 나누는 게 좋을까?
k-1개일 때와 k일 때를 비교해보면 됨!
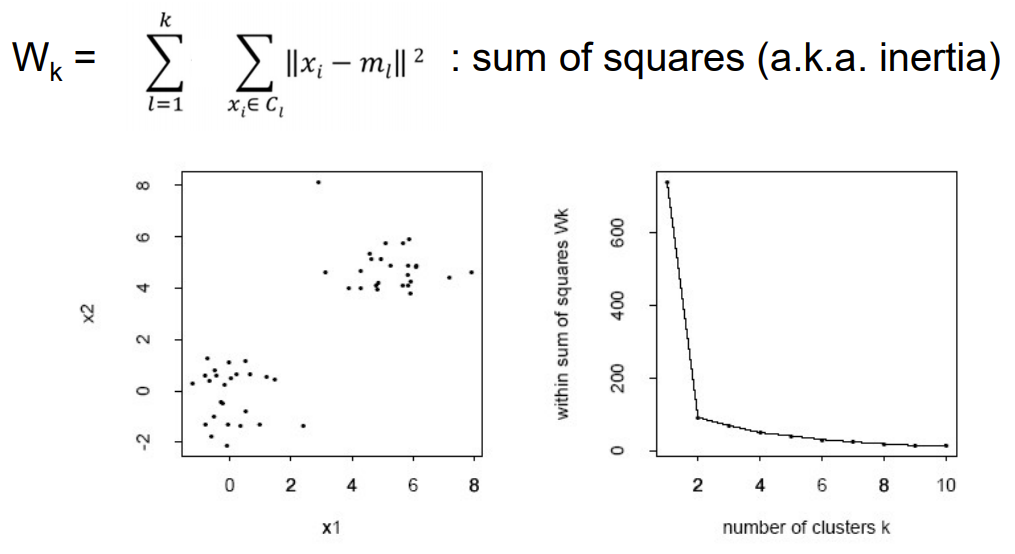
-
여기서는 2개가 적당할듯?
-
Gap Statistic
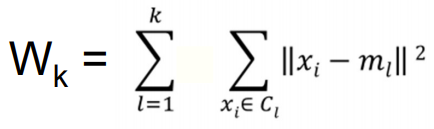
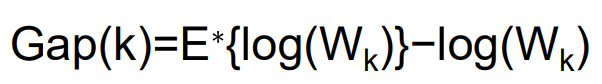
이 Gap(k)를 최대화 시킨다 =
clustering structure가 uniform distribution과 많이 다르다 =
잘 구분한다

2. Hierarchial 알고리즘
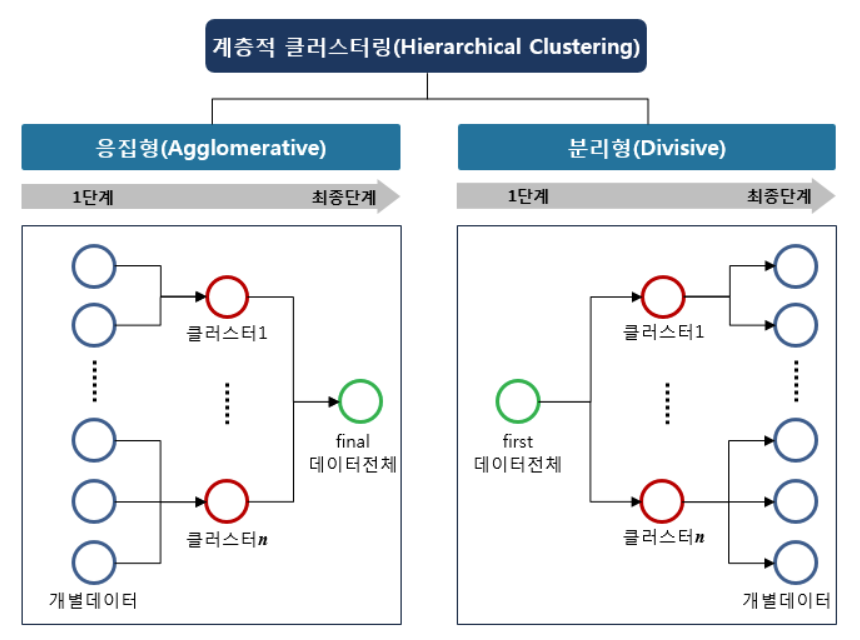
1. Top-down = divisive
두 개의 그룹으로 partition ➡ 재귀적으로 또 나눔
2. Bottom-up = agglomerative
한 군집에서 시작해서 두개의 군집을 비슷한(closest) 군집으로 묶는다
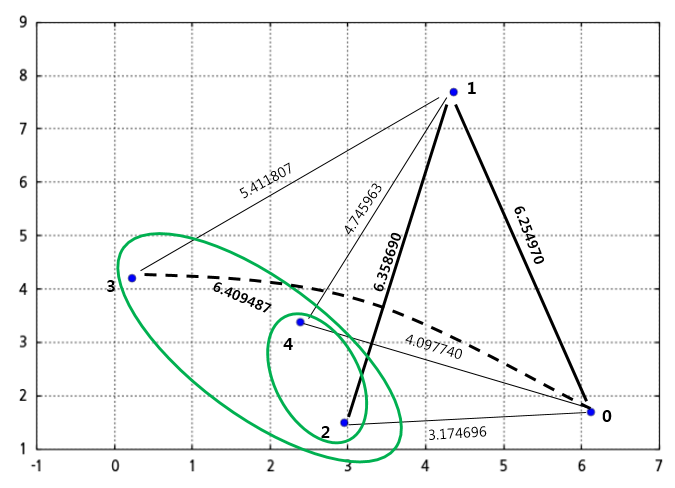
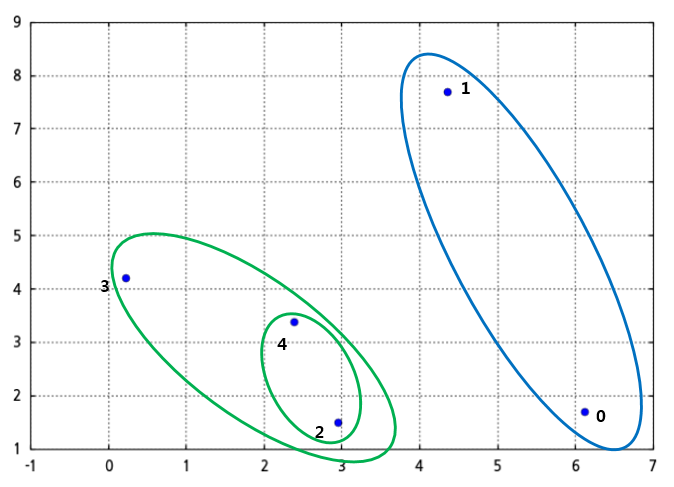
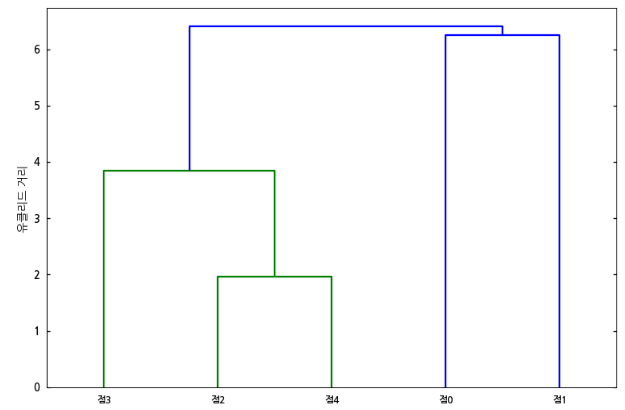
- 덴드로그램
군집 간 유사도 측정하기
- cosine similiar 하다 = 두 벡터가 가깝다 = 유사하다
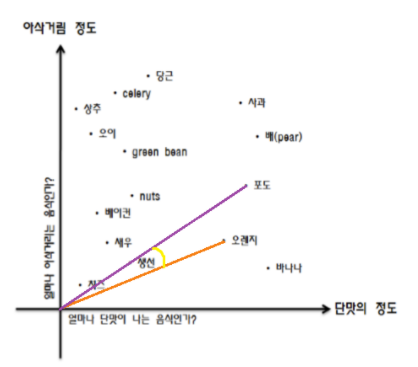
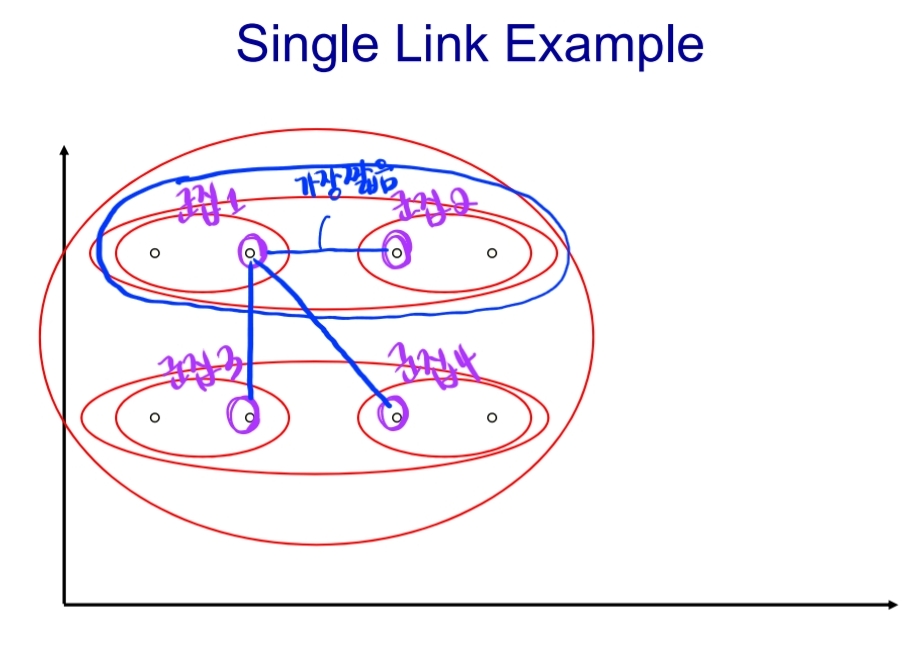
1) Single-link
군집간 비교할 때, 가장 유사한 점(cosine similar한 점)끼리 비교
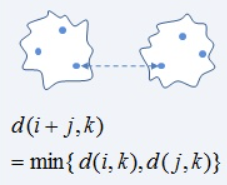
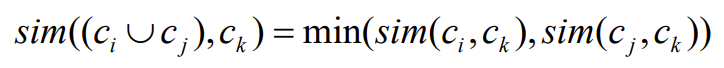
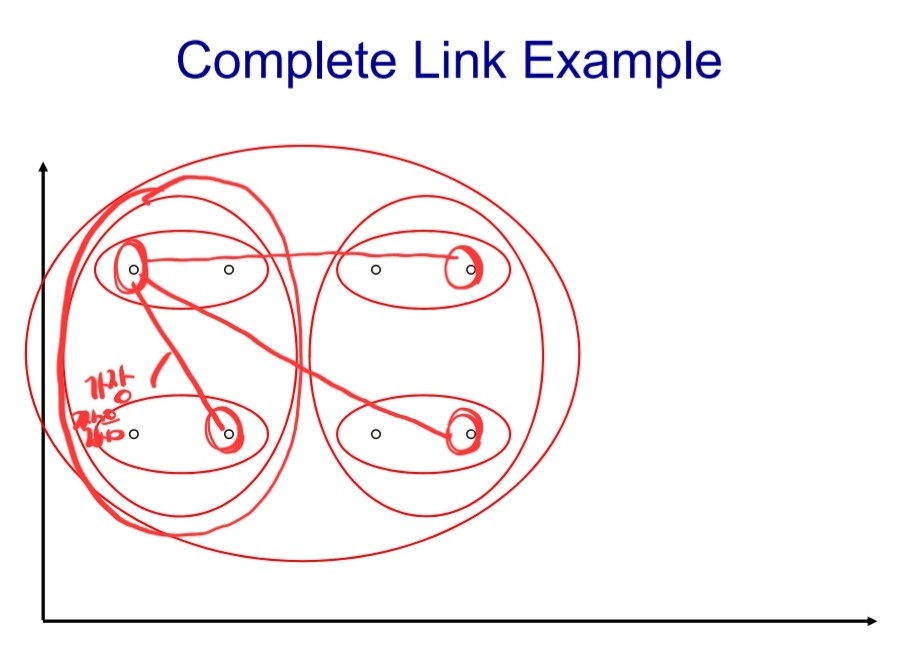
2) Complete-link
군집간 비교할 때, 가장 다른 점(cosine similar이 제일 작은 점)끼리 비교
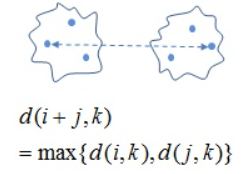
- 아래 두가지 예시로 비교해 보기
3) Centroid
두 군집의 Centroid끼리 비교
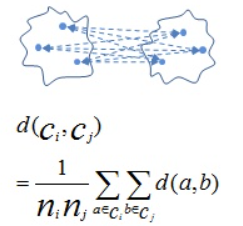
4) Average-link
pair들끼리 비교해서 average내기
5) 시간 복잡도
N개의 클러스터들로 시작해, N-1개의 merge들을 만들어냄

- 그런데, 우리는 이 모든 것을
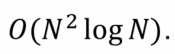
돌릴 수 있는 방법이 있다!
좋은 clustering의 기준
- intra-class(intra-cluster)의 similarity를 높이고
- inter-class의 similarity를 낮추고
Silhouette Coefficient
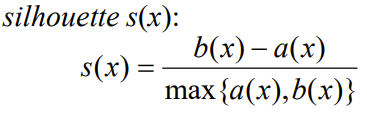
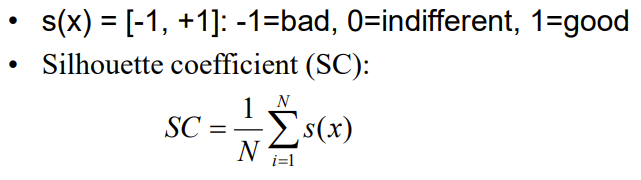
-
응집도 a(x) : 데이터 x와 동일한 클러스터 내의 나머지 데이터들과의 평균 거리
-
분리도 b(x) : 데이터 x와 가장 가까운 클러스터내의 모든 데이터들과의 평균거리
-
만약 클러스터 개수가 최적화 되어 있다면 b값은 크고(inter-class의 similarity 낮추기), a값은 작아짐(intra-class의 similarity 높이기)
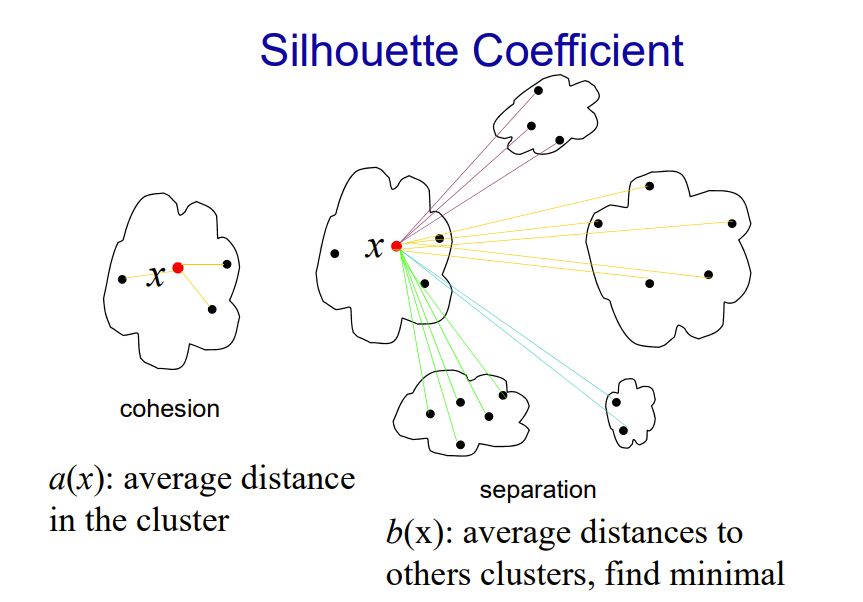
결론적으로, 최적 Cluster 개수 설정 방법은 두가지 인것
- elbow
- silhouette
