0-1 BFS

김두현·2024년 9월 24일

CS 이것저것...

목록 보기

7/8

백준 1354, 숨바꼭질 3 문제를 해결하다가 처음 접해본 BFS이다.

최단 경로를 해결하는 문제는 주로 다익스트라 알고리즘을 사용한다. 결과적으로 말하면 다익스트라의 시간 복잡도는 O(ElogE) 또는 (ElogV)인 반면에 0-1 BFS의 시간 복잡도는 O(V+E)의 시간 복잡도로 구현 가능하다.

💡 V → 정점의 갯수, E → 간선의 갯수

일단 기본 BFS(Breasdth-Fisrt Search)의 개념을 다 알고 있다고 생각하고 0-1 BFS 만의 특징을 위주로 설명하겠다.

0-1 BFS를 필요한 이유

처음에 숨바꼭질 3 문제를 해결하기 위해 기존의 숨바꼭질 시리즈와 같이 queue를 이용해 bfs로 해결하려고 했지만 예제 답과 계속 틀리게 나왔다. 그래서 생각한 결과 숨바꼭질 3 문제는 기존 숨바꼭질과 다르게 2 * x 이동의 가중치가 0이라는 점이다.

이 때문에 기존 bfs로 해결하는 문제는 정점에서 정점으로의 이동, 레벨, 가중치가 동일해 정점 방문 횟수가 곧 가중치가 되므로 가중치가 0인 edge가 있으니 해결이 안 되는 것이다.

그래서 가장 일반적인 방식은 다익스트라 알고리즘을 통해 각 가중치에 대한 최단 거리를 찾는 방법이다.

아마 다익스트라 알고리즘으로도 문제 해결은 가능하다고 생각하지만 0-1 bfs 풀이를 통해 좀 더 직관적이고 속도 또한 빠르게 해결할 수 있다.

그래서 0-1 BFS가 뭔데?

이름과 같이 0 과 1로 가중치가 edge에 부여된 그래프에서 최단 경로를 구할 수 있는 알고리즘이다.

큰 탐색 순서는 일반적인 bfs와 동일하지만 몇 가지 조건이 붙는다.

가중치가 0인 edge가 존재하기 때문에 정점의 방문 횟수 보다 가중치가 더 낮은 경우를 먼저 고려해야 한다.
결과 값이 방문 횟수의 최소가 아닌 가중치의 최소인 경로를 탐색해야 한다.

이를 구현하기 위해 기존의 Queue 대신 → Deque 자료구조를 사용한다.

Deque
deque는 간단히 말해 front, back 위치에서 모두 입출력이 가능한 queue라고 생각하면 쉽다.

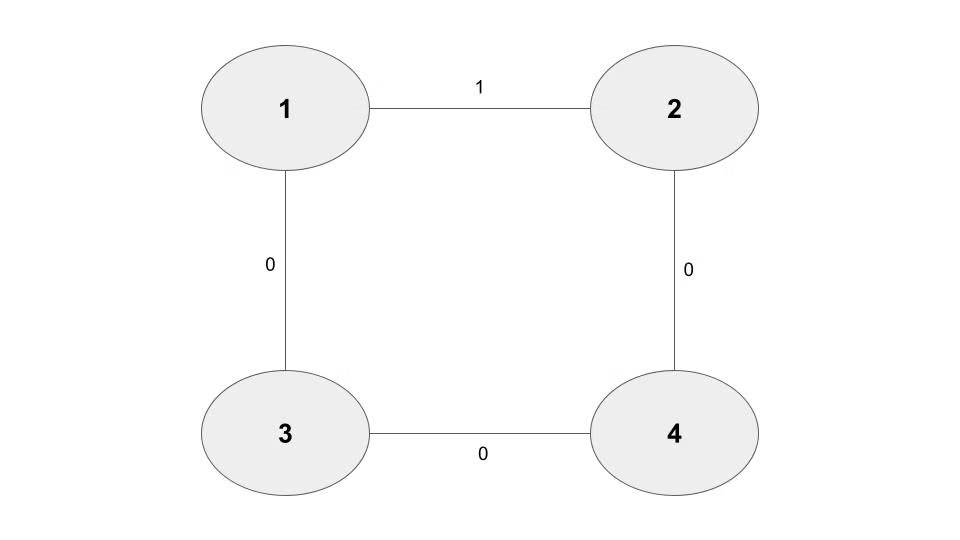
위와 같은 정점과 간선으로 이루어진 그래프에서 정점 1에서 정점 2까지 최소 경로를 구하고 싶을 때를 생각해보자.

기존의 bfs(queue)로 구현한 풀이에서 최소 경로는 1 → 2 로 바로 이동하는 비용이 2인 값이 나올 것 이다.

하지만 1 -> 3 -> 4 -> 2 경로가 비용이 0인 최소 경로라고 할 수 있다! 이처럼 방문 횟수보다 가중치를 고려하도록 bfs를 수정할 필요가 있다.

0-1 BFS 구현

이제 그럼 구체적인 0-1 bfs를 구현하기 위한 알고리즘을 알아보자.

일반 Queue 대신 Deque 사용
가중치가 0인 간선을 통해 도착한 정점은 deque의 front에 추가
가중치가 1인 간선을 통해 도착한 정점은 deque의 back에 추가
pop은 기존과 같이 front에서 pop

python를 기준으로 각각 특징을 구현하는 코드를 알아보자

# 1. deque 사용
from collections import deque

deq = deque()

# 2. 가중치 0 -> front에 추가
deq.appendleft("Node")

# 3. 가중치가 1 -> back에 추가
deq.append("Node")

# 4. pop
node = deq.popleft()

위의 로직만 일반적인 bfs에서 수정하면 0-1 bfs를 쉽게 구현할 수 있다!

숨바꼭질 3

문제 자체는 단순하다.

N 위치에서 K 위치(N, K는 정수)까지 이동하는데 가장 최단 경로가 무엇이냐?

기존의 숨바꼭질과 같이 -1, +1, X2 이동이 있지만 X2 이동은 가중치가 0인 점만 다르다.

아래 코드는 숨바꼭질 3 문제를 해결한 코드이다.

import sys
from collections import deque

input = sys.stdin.readline

N, K = map(int, input().split())
visited = [1000000] * 100001
visited[N] = 0

def move(n, i):
    if i == 0:
        return n * 2
    elif i == 1:
        return n - 1
    else:
        return n + 1

def bfs(N, K):
	deq = deque()
	deq.append((N, 0))

	while deq:
		num, time = deq.popleft()
		if num == K:
			return visited[num]

		for i in range(3):
			next = move(num, i)
			if 0 <= next <= 100000 and visited[next] == 1000000:
				if i == 0:
						visited[next] = time
						deq.appendleft((next, visited[next]))
				else:
						visited[next] = time + 1
						deq.append((next, visited[next]))

print(bfs(N, K))

visited 배열에 N -> K 까지 이동하는 최단 거리가 저장
visited 배열 초기 값은 1,000,000 으로 초기화 → visited[i] == 1,000,000 이라면 아직 방문하지 않은 정점
- 1,000,000 값은 N, K 보다 충분히 큰 값이라는 의미로 사용 like INT_MAX
move 함수를 통해 현재 위치 n에서 다음 위치를 계산
i == 0 -> 순간 이동 : 가중치가 0인 정점으로 이동이므로 덱의 front에 추가
else -> +1 or -1: 가중치가 1인 정점으로 이동이므로 덱의 back에 추가