https://www.acmicpc.net/problem/1520
문제 소개
백준 골드 3 수준의 문제로 (0, 0) 위치에서 출발해 (N - 1, M - 1) 위치까지 이동하는 모든 경로의 개수를 구하는 문제다. 아래와 같은 추가적인 조건이 붙는다.
- 한 칸에서 인접한 상하좌우로만 이동이 가능하다.
- 각 칸마다 값이 있는데 현재 칸보다 이동할 칸의 값이 작아야 이동 가능하다.
말 그래도 내리막길 경로 중에서 가능한 경로의 개수를 출력하는 것이다!
문제 접근 법
초기 접근
처음에는 단순히 “내리막길” 이라는 조건이 붙은 dfs 문제로 접근해 골드 3 수준인가? 생각했다.
아래 코드와 같이 단순히 dfs 방식으로 모든 칸을 방문하면서 (N - 1, M - 1) 칸까지 도착하면 answer 값을 1 증가했다. 다행히 백준에서 제공하는 예제와 같은 값이 나와 정답인 줄 알았다…
import sys
sys.setrecursionlimit(10010)
input = sys.stdin.readline
N, M = map(int, input().split())
matrix = [list(map(int, input().split())) for _ in range(N)]
answer = 0
def dfs(pos, visited):
visited[pos[0]][pos[1]] = 1
if pos == (N - 1, M - 1):
global answer
answer += 1
return
for m in [(0, 1), (1, 0), (0, -1), (-1, 0)]:
next = (pos[0] + m[0], pos[1] + m[1])
if 0 <= next[0] < N and 0 <= next[1] < M and not visited[next[0]][next[1]]:
if matrix[next[0]][next[1]] >= matrix[pos[0]][pos[1]]:
continue
dfs(next, visited)
visited[next[0]][next[1]] = 0
dfs((0, 0), [[0] * M for _ in range(N)])
print(answer)
한 18%에서 계속 시간 초과가 발생해 다른 사람들의 작성한 게시글을 보면서 해결했다.
<반례>
18 18
36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19
35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18
34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17
33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16
32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15
31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14
30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13
29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12
28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11
27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10
26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9
25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8
24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7
23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6
22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5
21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4
20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3
19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 10000
위의 반례처럼 도착지 칸의 값이 커 경우의 수가 0일 때도 단순 dfs는 약 4 ^ (18 * 18) 정도의 각 노드를 탐색하므로 무조건 시간 초과가 터질 수 밖에 없다!!
올바른 접근
해당 문제를 시간 내에 해결하기 위해서는 dfs에 dp 접근 법을 추가해서 해결할 수 있다.
dp = [[-1] * M for _ in range(N)]
- dp[x][y] → 임의의 지점 (x, y)에서 (N - 1, M - 1) 까지 이동할 수 있는 경로의 수
- dp[x][y] == sum(이웃한 4 방향 노드의 경우 수) == dp[x - 1][y] + dp[x + 1][y] + dp[x][y - 1] + dp[x][y + 1]
dfs 방식을 사용하면 (0, 0)에서 bfs와 달리 순서대로 근처 노드들을 하나하나 방문하는 것이 아닌 도착 노드까지 갈 수 있는 가장 이동이 적은 경로로 map을 탐색하게 된다. 이 과정에서 모든 경로의 수를 반복하기 위해 재귀를 통해 탐색을 계속 하게 되면 방문했던 노드를 또 방문하게 된다.
만약 (x, y) 노드를 이전 경로에서 방문해 dp[x][y](경로/경우의 수) 값을 구했다면 다시 계산할 필요가 없이 바로 함수를 종료하므로 시간을 크게 단축 가능하다!!
- 초기 값이 -1 인 N * M 크기의 2차원 배열 dp를 선언
- (0, 0) → (N - 1, M - 1) 까지 내리막길이 있다면 dfs을 통해 끝 점까지 도착
- 함수를 종료 방문했던 노드로 돌아오면서 이웃한 4 방향 노드 값을 Add
- 최종 dp[0][0]에 (N - 1, M - 1) 까지 경로의 수가 저장
dfs((x, y)) 함수가 종료된다는 것은 해당 지점에서 갈 수 있는 모든 이웃한 방향을 탐색했다는 의미!
dp 초기 값을 0으로 세팅 시 도착 경로가 없을 경우 계속 0으로 업데이트 → 방문한 노드인지 판별 불가
정답 코드
import sys
sys.setrecursionlimit(10010)
input = sys.stdin.readline
N, M = map(int, input().split())
matrix = [list(map(int, input().split())) for _ in range(N)]
dp = [[-1] * M for _ in range(N)]
def dfs(pos):
if dp[pos[0]][pos[1]] != -1:
return dp[pos[0]][pos[1]]
if pos == (N - 1, M - 1):
return 1
sum = 0
for m in [(0, 1), (1, 0), (0, -1), (-1, 0)]:
next = (pos[0] + m[0], pos[1] + m[1])
if 0 <= next[0] < N and 0 <= next[1] < M:
if matrix[next[0]][next[1]] >= matrix[pos[0]][pos[1]]:
continue
sum += dfs(next)
dp[pos[0]][pos[1]] = sum
return dp[pos[0]][pos[1]]
print(dfs((0, 0)))
|

|
|
|
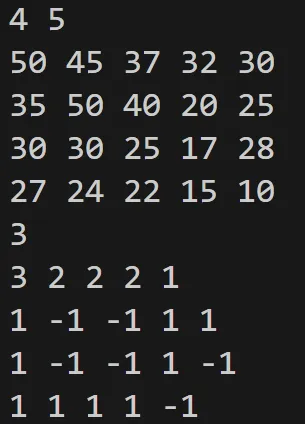
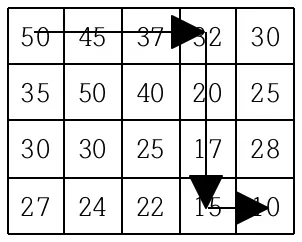
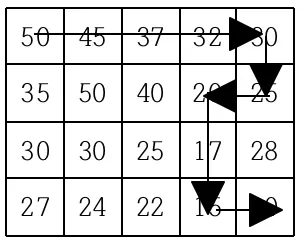
가장 왼쪽 이미지가 예제 입력일 때 결과 값과 추가적으로 dp 배열을 출력한 이미지이다. 해당 출력 값을 통해 나머지 이미지가 나타내는 세 경로를 유추할 수 있다.