📌 1. Bellman-Ford Algorithm 설명
벨만포드 알고리즘은 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이다.
최단 거리 혹은 최소 비용 중에서도, 주어진 두 노드(시작노드, 도착노드) 사이의 최소 비용인 경로를 찾을 때 유용하게 사용된다.
다익스트라와 다른 특징은 간선의 가중치가 음수일 때도 최단 거리를 구할 수 있다.
벨만포드 알고리즘은 '모든 경우의 수를 다 탐색해 가면서 최소비용'을 찾게 된다.
다익스트라 알고리즘과는 달리 그리디 하지 않게 동작한다. 다익스트라 알고리즘은 "지금 당장 눈앞에 보이는, 연결되어 있는
정점들 중에서 최소비용으로 연결된 정점을 선택" 하는 방식, 즉, 그리디스럽게 접근했다면 벨만포드 알고리즘은 그리디 하지 않고, 모든 경우의 수를 탐색하는 동작 원리를 가지고 있다.
벨만포드 알고리즘의 동작원리는 다음과 같다.
- 모든 간선들을 탐색하면서, 간선이 잇는 출발정점이 '한번이라도 계산 된 정점' 이라면 해당 간선이 잇는 정점의 거리를 비교해서 업데이트 한다.
- 1번 과정을 반복한다.
이 사진으로 예시를 든다면, 1번 정점을 시작점으로 잡고, 1번 정점을 거리가 0이라고 계산했다고 가정해보자.
그럼, 1 → 2 를 잇는 간선에 의해서 2번 정점이 계산될 것이고 (2번 정점 계산됨)
그 이후, 2 → 3을 잇는 간선에 의해서 3번 정점이 계산될 것이고 (3번 정점 계산됨)
그 이후, 3 → 4를 잇는 간선에 의해서 4번 정점이 계산될 것이다. (4번 정점 계산됨)
총 3번 반복했더니, 모든 정점의 거리를 구할 수 있었다.
즉 정점의 총 갯수를 N 개라고 가정한다면, 위에서 말한 '1번과정'을 총 N-1번 반복하면 된다.이제 실전으로 들어가보자.
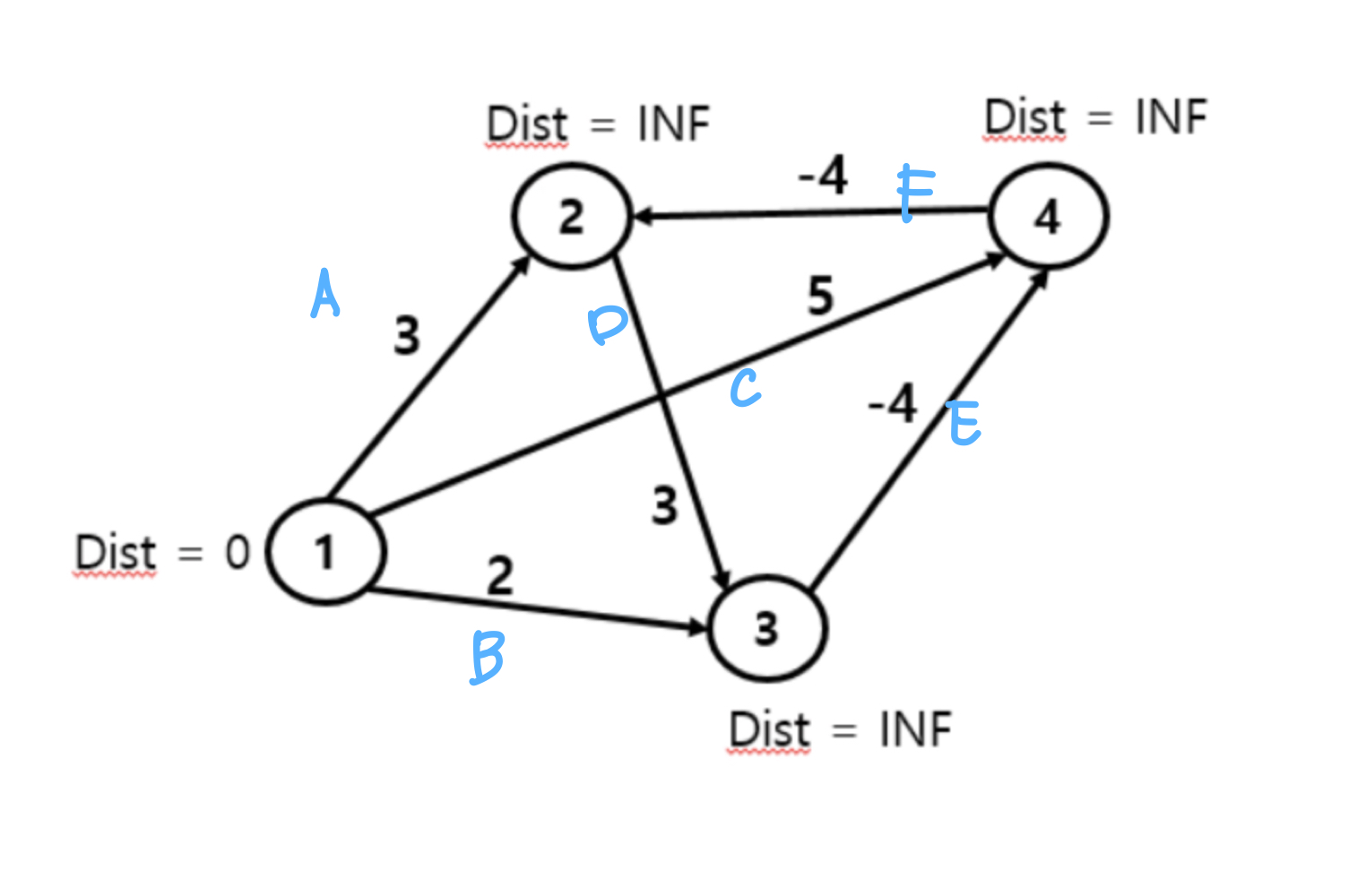
A에서 F 순서대로 탐색한다고 가정해보자.
★ 간선 'A'는 1 → 2 로 가는 비용이 '3'이 드는 간선인데, 기존의 정점 '2'의 비용은 무한대 이기 때문에, 정점2의 비용이 3으로 업데이트 될 것이다. 이 순간 정점2는 '이미 한번이라도 계산된 정점' 이 된다.
★ 간선 'B'는 1 → 3 으로 가는 비용이 '2'가 드는 간선인데, 기존의 정점 '3'의 비용은 무한대 이기 때문에, 정점 3의 비용이 '2'로 업데이트 될 것이다. 이 순간 정점 3은 '이미 한번이라도 계산된 정점'이 된다.
★ 간선 'C'는 1 → 4로 가는 비용이 '5'가 드는 간선이다. '1'은 이미 한번이라도 계산된 정점이므로 이 간선에 의해서 업데이트가 발생할 수 있고, 정점 '4'로 가는데 드는 비용이 5로 업데이트가 될 것이다.
★ 간선 'D'는 2 → 3 으로 가는 비용이 '3'이 드는 간선이다. 정점 '2'는 이미 한번이라도 계산된 정점이기 때문에(A 간선에 의해서 계산이 한번 되었음) 이 간선에 의해서 업데이트 되는 비용이 있는지 확인해보자.
2 → 3 으로 가는데 비용이 '3'이 들게 되고, 현재 정점 '3'의 비용은 '2' 이다. 그럼 값을 비교해보자.
1 → 2 로 가는데 비용이 '3'이 들었고, 2 → 3 으로 가는데 비용이 '2' 가 들게 되므로, 총 '5'의 비용이 발생한다.
하지만 정점 '3'의 현재까지의 최소비용은 '2' 이기 때문에 5 > 2 이므로, 업데이트가 발생하지 않는다.
★ 간선 'E'는 3 → 4로 가는데 비용이 -4 가 드는 간선이다. 현재 정점 '4'의 최소비용은 '5'이다.
그럼 계산을 해보면 1 → 3 으로 가는데 비용이 '2' , 3 → 4 로 가는데 비용이 -4, 더해보면 2 - 4 = -2 로 현재까지의 정점 '4'의 최소비용인 5보다 더 작은 값이 된다. 따라서 정점'4'의 비용에 업데이트가 발생한다.
★ 간선 'F'는 4 → 2로 가는 비용이 -4가 드는 간선이다. 현재 정점 '2'의 최소비용은 '3'이다.
그럼 1 → 4로 가는데 현재까지의 최소비용은 '-2' 이고, 4 → 2 로 가는데 드는 비용이 -4 이므로, 총 -6의 비용이 발생한다. 현재까지의 정점'2'의 최소비용인 '3'보다 더 작은 값이므로 업데이트가 발생한다.
이렇게 탐색을 한번 하고 나면 아마 정점들의 최소비용이 다음과 같이 업데이트 되어 있을 것이다.
우리는 지금까지 N - 1번동안 모든 간선들에 대해서 가중치를 업데이트 해 왔다.
왜냐하면, N - 1번 탐색을 하게되면 모든 정점에 들어가는 최소비용을 구할 수 있기 때문이였다.
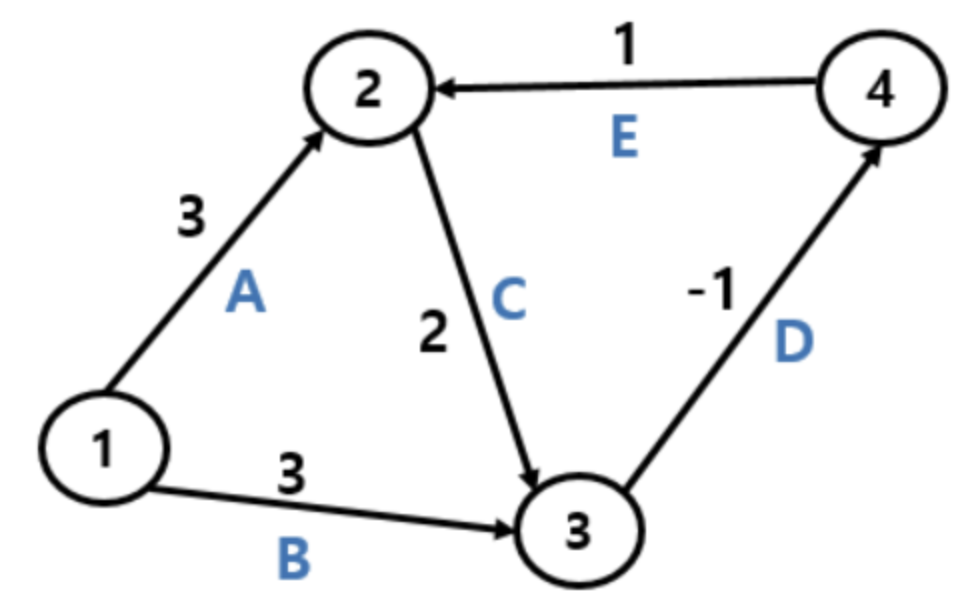
그런데 이 만큼 탐색을 하고, 딱 한번만 더 탐색을 해보는 것이다. 정상적이였다면, 더 이상의 비용이 업데이트 되지 않을 것이다. 그럼 정상적인 상황을 그림으로 한번 봐보자. 빠르게 위에서 말했던 과정을 진행해보자.
★ 1번 정점을 이미 한번이라도 계산된 정점을 만들어 주기 위해서 Dist[1] = 0 으로 설정.
★ 간선 'A'에 의해서 '2'번 정점의 비용이 '3'으로 업데이트. (2번은 한번이라도 계산된 정점)
★ 간선 'B'에 의해서 '3'번 정점의 비용이 '3'으로 업데이트. (3번은 한번이라도 계산된 정점)
★ 간선 'C'에 의해서 업데이트가 발생하지 않는다
★ 간선 'D'에 의해서 '4'번 정점의 비용이 '2'(3 - 1)로 업데이트. (4번은 한번이라도 계산된 정점)
★ 간선 'E'에 의해서 업데이트가 발생하지 않는다. 4번 정점으로 가는데 드는 비용은 '2' 이고, 4 → 2로 가는 간선 'E'에 의해서 계산을 하더라도, 2 + 1 = 3 으로 기존의 정점 '2'의 비용인 3과 동일하기 때문에 업데이트 되지 않는다
이렇게 한번 계산을 했다. 우리는 총 N - 1번, 즉 3번 계산을 해야 하므로 2번 더해보자.
★ 'A'에 의해서 업데이트 발생하지 않음.
★ 'B'에 의해서 업데이트 발생하지 않음.
★ 'C'에 의해서 업데이트 발생하지 않음.
★ 'D'에 의해서 업데이트 발생하지 않음.
★ 'E'에 의해서 업데이트 발생하지 않음.
이렇게 한번 더 해봤는데, 한번 더 하더라도 위와 결과가 동일하게 발생한다.
사실, 위의 그래프가 굉장히 지금 상황을 설명하기 별로인 것 같지만, 하고자 했던 말은 이것이다.
"정상적인 그래프라면, 즉, 음의 사이클이 발생하지 않는 그래프라면, N - 1번을 탐색한 이후에, 또 한번의 탐색을 더 하더라도 절대로 ! 최소비용이 변하는 정점이 발생하지 않는다" 라는 것이다.
위의 그래프가 별로라고 했던 것은, 1번만 탐색을 했는데도 더 이상 최소 비용이 변하지 않는 그래프라서 별로라고 한 것이다.
그럼 본론으로 다시 돌아와서, 벨만포드 알고리즘에서 '음의 사이클'이 존재한다는 것을 어떻게 판단할까 ??
바로, "N - 1번 모든 간선을 탐색 후, 한번 더 모든 간선을 탐색" 을 진행하면 된다.
그렇게 한다면 ?? '음의 사이클'을 가진 그래프였다면, 이 '한번 더 탐색'하는 과정에서 최소비용이 변하는 정점이 있을 것이다.
위에서 봤듯이, '2'번 정점이 탐색을 하면 할수록 계속해서 최소비용이 바뀐 것과 같이 !
따라서, 벨만포드 알고리즘은 이렇게 음의 가중치가 존재할 때, '음의 사이클'이 존재하는지 안하는지까지 파악할 수 있는
알고리즘이다.
다익스트라 알고리즘에 비해서 최소 비용을 찾는 시간이 일반적으로 더 오래 걸리는 알고리즘이지만, 이러한 부분 때문에
다익스트라 알고리즘에서는 할 수 없었던 경우를 벨만포드 알고리즘으로는 해결할 수 있고, 벨만포드 알고리즘을 사용하는
것이다. 따라서 아래와 같이 벨만포드 코드를 구현할 수 있다.
void Bellman_Ford()
{
Dist[1] = 0;
for (int i = 1; i <= N - 1; i++)
{
for (int j = 0; j < Edge.size(); j++)
{
int From = Edge[j].first.first;
int To = Edge[j].first.second;
int Cost = Edge[j].second;
if (Dist[From] == INF) continue;
if (Dist[To] > Dist[From] + Cost) Dist[To] = Dist[From] + Cost;
}
}
for (int i = 0; i < Edge.size(); i++)
{
int From = Edge[i].first.first;
int To = Edge[i].first.second;
int Cost = Edge[i].second;
if (Dist[From] == INF) continue;
if (Dist[To] > Dist[From] + Cost)
{
cout << "음의 사이클이 존재하는 그래프입니다." << endl;
return;
}
}
cout << "음의 사이클이 존재하지 않는, 정상적인 그래프 입니다." << endl;
}
Dist배열의 초기상태는 모두 'INF(무한대)' 로 초기화 되어 있는 상태이다.
그리고, 'Edge'는 간선의 정보를 저장한 vector인데, Edge에는 { 시작점, 도착점, 비용 } 이 저장되어 있다.
라인별로 어떤 역할을 하는지 알아보자.
line3)
- 가장 처음에 '1'번 정점을 "이미 한번이라도 계산된 정점" 이라고 표시해주기 위해서 1번정점의 Dist값을 0으로 바꿔주는 부분이다. 이 부분이 없다면, 모든 간선을 탐색하는 부분에서, "이미 한번이라도 계산된 정점"이 하나도 없기 때문에 어떠한 값도 계산이 되지 않는 문제가 발생한다.
line4 ~ 15)- line4)를 보면 1 ~ N - 1 까지, 총 N - 1번 반복한다는 것을 알 수 있다.
위에서도 말했듯이, "모든 정점을 가는데 드는 최소비용을 알기 위해서는 최소 'N - 1'번 탐색"을 해봐야 하기 때문이다.- line6 ~ 13)을 보면, 모든 간선을 탐색하면서, 정점에 드는 최소비용을 업데이트 하는 과정인데, line12 에 주목하자.바로 "이미 한번이라도 계산된 정점" 인지 아닌지 판단하는 부분이다. 이미 한번이라도 계산된 정점 이라면 Dist의 값이 무한대가 아닐 것이다.
line17 ~ 29)- 그래프가 '음의 사이클'을 갖는지 판단하기 위해서, N - 1번 탐색 후 ! 한번 더 모든 간선들을 탐색하는 부분이다.
정상적인 그래프라면 저 과정에서 더 이상 최소비용이 업데이트 되는 정점은 없을 것이다.
하지만, 음의 사이클을 갖는 그래프라면, 최소비용이 업데이트 되는 정점이 발생할 것이다. 따라서 그런 경우
line26)에서 출력 후 바로 return을 시켜주는 부분이다.
📌 2-1 Leet code 743번 네트워크 딜레이 시간 - 다익스트라를 활용하여
문제 : 1에서 n까지 레이블이 지정된 n 개의 노드로 구성된 네트워크가 제공됩니다. 또한 시간, 이동 시간 목록을 지정 에지로 제공합니다. times [i] = (ui, vi, wi), 여기서 ui는 소스 노드, vi는 대상 노드, wi는 걸리는 시간입니다. 소스에서 타겟으로 이동합니다. 주어진 노드 k에서 신호를 보냅니다. 모든 n 개의 노드가 신호를 수신하는 데 걸리는 시간을 반환합니다. n 노드가 모두 신호를 수신 할 수없는 경우 -1을 반환합니다.
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
graph = collections.defaultdict(list)
for a, b, cost in times:
graph[a].append((b, cost))
q = [(0, k)]
dist = collections.defaultdict(int)
while q:
time, node = heapq.heappop(q)
if node not in dist:
dist[node] = time
for v, w in graph[node]:
alt = time + w
heapq.heappush(q, (alt, v))
print(dist)
if len(dist) == n:
return max(dist.values())
return -1제출 결과는 성공입니다. (추가로 이미지를 첨부하지 않았습니다.)
📌 2-2 Leet code 743번 네트워크 딜레이 시간 - 벨만포드를 활용하여
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
constexpr int MAX_TIME = 101 * 100;
vector<int> dist(N, MAX_TIME);
dist[K - 1] = 0;
for (int i = 1; i < N; ++i)
for (const auto& time : times) {
int u = time[0] - 1, v = time[1] - 1, w = time[2];
dist[v] = min(dist[v], dist[u] + w);
}
int max_dist = *max_element(dist.begin(), dist.end());
return max_dist == MAX_TIME ? -1 : max_dist;
}
};아직 이 코드는 이해가 좀 어렵습니다... 조금더 공부해야 이해될 것 같습니다.
📌 3-1 백준 문제 1916번 최소비용 구하기 - 다익스트라를 활용하여
#include <bits/stdc++.h>
using namespace std;
#define INF 987654321
using pii= pair<int, int>; //도시 A에서 도시 B까지 가는 거리 저장
//s는 출발점 도시 번호, e는 도착점 도시 번호, w는 s에서 e로 가는데 소요되는 비용이다.
vector<pii> vec[1001];
vector<int> dist(1001, INF);
void dijkstra(int dept){
dist[dept] =0;
priority_queue<pii> pq;
pq.push({dist[dept], dept}); // 시작 weight, vertex
while(!pq.empty()){
int cur = pq.top().second;
int distance = pq.top().first * -1; //현재까지 dept에서 cur 정점까지 가는 dist
pq.pop();
if(dist[cur]<distance) continue; //이미 distance가 최소로 변경됨
/* 우선 pq에서 가장 top에 있는 pair를 뺀다. pq에서 저장되어 있던 pair중 가장 cost가 작은 pair를 꺼내 vertex와 cost를 저장한다.
만약 dist[cur]이 pq에서 꺼내온 cur의 cost보다 작다면 이미 해당 vertex에 대해서 최소 비용으로 계산이 된것을 뜻하기 때문에 방문이 됐다고 간주하고 넘어간다.
예를 들어 처음 시작 정점과 연결된 vertex와 비용이 pq에 모두 들어간다.
pq = ({-1, 4}, {-10, 5} ...) 와 같다고 치자!
만약 pq에서 4번 정점을 빼와서 계산을 하다보니 start-4-5로 가는 비용이 더 적어 dist[5]에 변화가 일어났다고 생각하면 pq는 아래와 같이 변화될 수있다.
pq = ( {-4, 5}, {-10, 5} ...)
그럼 또 현재 dist[5]= 4이고 pq내에 있는 비용 4와 10은 조건에 의해서 아래 최소비용 계산을 진행하지 않는다. 그렇기 때문에 자연스럽게 이미 방문했던 vertex를 방문하지 않게 되는 것!*/
for(int i=0; i<vec[cur].size(); i++){
int nxt=vec[cur][i].first; //cur 정점과 연결된 정점들
int nxtdist = vec[cur][i].second + distance;
//현재까지 dept에서 cur정점까지의 최소 거리와
//cur을 지나 nxt까지의 거리를 더한것 cur정점에서 nxt까지의 distance
// e.g) 1 -> 4(cur) -> 5(nxt)
if(nxtdist<dist[nxt]){//만약 cur을 지나가는 것이 더 가깝다면
dist[nxt]= nxtdist;
pq.push({nxtdist*-1, nxt});//새롭게 갱신된 weight와 vertex
}
}
}
}
/*이제 cur과 연결되어 있는 정점들에 대해서 계산한다. 계산을 진행한다는 dept-> cur -> nxt의 비용이 더 적은지 dept-> nxt의 비용이 더 적은지 확인해보겠다는 얘기다.
만약 dept에서 nxt까지 가는 비용이 10이었는데, cur을 지나 nxt를 가는 경우는 4라고 치쟈! 그러면 dist[nxt]를 업데이트 해주는것이다. dist[nxt]를 업데이트 한다는 것은 dept에서 nxt정점까지 가는 비용이 더 적어졌다는 얘기. */
int main(){
int N, M; cin>>N>>M;//도시의 개수, 버스의 개수
while(M--){
int s, e, w; cin>>s>>e>>w;
vec[s].push_back({e, w});
}
int dept, dest;
cin>>dept>>dest;
dijkstra(dept);
cout<<dist[dest];
return 0;
}📌 3-2 백준 문제 1916번 최소비용 구하기 - 벨만포드를 활용하여
#include <iostream>
#include <vector>
#define INF 987654321
using namespace std;
/*
벨만포트 알고리즘
마지막 V번에서도 완화가 되면 음수 사이클이 존재함을 알려준다.
*/
int V,M;
vector<pair<int, int> > v[1001];
int upper[1001];
int bellmanFord(int src) {
//시작점 제외 모든 정점까지의 최단거리 INF로 초기화
fill_n(upper, 1001, INF);
upper[src] = 0;
bool updated;
for(int i = 0; i < V; i++) {
updated = false;
for(int j = 1; j <= V; j++)
for(int k = 0; k < v[j].size(); k++) {
int there = v[j][k].first;
int cost = v[j][k].second;
if(upper[there] > upper[j] + cost) { // 완화 성공
upper[there] = upper[j] + cost;
updated = true;
}
}
if(!updated) break; //모든 간선에 대해 완화가 실패할경우 break;
}
if(updated) return 1; //음수 사이클이 존재
return 0;
}
int main(void) {
//ios_base::sync_with_stdio(false); cin.tie(NULL);
cin >> V >> M;
for(int i = 0; i < M; i++) {
int a,b,c;
cin >> a >> b >> c;
v[a].push_back(make_pair(b, c));
}
int start, arrive; cin >> start >> arrive;
if(!bellmanFord(start))
cout<<upper[arrive];
return 0;
}