📌 코드 중심으로 살펴보는 그래프 표현 방법
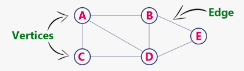
그래프(Graph)란?
A. 단순히 노드(N, node)와 그 노드를 연결하는 간선(E, edge)을 하나로 모아 놓은 자료 구조
그래프 관련 용어 정리
-정점(vertex): 위치라는 개념. (node 라고도 부름)
-간선(edge): 위치 간의 관계. 즉, 노드를 연결하는 선 (link, branch 라고도 부름)
-인접 정점(adjacent vertex): 간선에 의 해 직접 연결된 정점
-정점의 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
무방향 그래프에 존재하는 정점의 모든 차수의 합 = 그래프의 간선 수의 2배
-진입 차수(in-degree): 방향 그래프에서 외부에서 오는 간선의 수 (내차수 라고도 부름)
-진출 차수(out-degree): 방향 그래픙에서 외부로 향하는 간선의 수 (외차수 라고도 부름)
방향 그래프에 있는 정점의 진입 차수 또는 진출 차수의 합 = 방향 그래프의 간선의 수(내차수 + 외차수)
-경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
-단순 경로(simple path): 경로 중에서 반복되는 정점이 없는 경우
-사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우방향, 가중치로 구분할 수 있다. 단순하게는 선에 화살표가 있으면 방향이 있는 것, 선에 숫자가 써있으면 가중치가 있는 것이라고 생각하면 된다.
그래프를 표현하는 2가지 방식?
- 인접 행렬(Adjacency Matrix): 2차원 배열을 사용하는 방식
- 인접 리스트(Adjacency List): 리스트를 사용하는 방식
인접행렬
인접 행렬이란?
이름 그대로 그래프의 연결 관계를 행렬로 표현하여 이차원 배열로 나타내는 방식을 의미한다. 인접 행렬 adj[i][j] 을 아래와 같이 정의할 수 있다.
adj[i][j] : 노드 i에서 j로 가는 간선이 존재할 경우 1, 아니면 0
만일 표현하고자 하는 그래프가 방향이 없는 무향 그래프의 경우에는 노드 i에서 노드 j로 가는 길이 존재하면 노드 j에서 노드 i로 가는 길 또한 존재한다. 이러한 특성으로 인접행렬을 구현할 경우, 대각 성분을 기준으로 대칭인 성질을 갖게 된다.
인접 행렬의 장단점은?
구현이 매우 간단하다는 것이다.
또한, 노드 끼리의 연결여부를 확인하고 싶을 때는, adj[i][j]의 값이 1인지 0이지만 확인하면 되기 때문에 O(N)이라는 시간 복잡도에 확인이 가능하다는 장점이 있다. 그러나, 만일 전체 노드의 개수가 V개, 간선의 개수가 E개라고 가정해보았을때, 노드 i에 연겨된 모든 노드들에 방문을 하고자 할 경우, adj[i][1] ~ adj[i][v]까지 모두 확인해봐야 하기 때문에 노드의 갯수에 비례하는 O(V) 복잡도를 갖는다. 위 단점으로 인해 노드의 개수에 비해 간선의 개수가 훨씬 작은 그래프라면 효율은 비례하여 낮아질 것이다.
따라서 무방향 그래프일때 예시 코드는 다음과 같다.
#include <iostream>
using namespace std;
int n, m;
int adj[10][10];
int main() {
cin >> n >> m;
for (int i=0; i<m; i++) {
int a, b;
cin >> a >> b;
adj[a][b] = 1;
adj[b][a] = 1;
}
}인접리스트
인접 리스트란?
각각의 노드에 연결된 노드들을 원소로 갖는 리스트들의 배열을 의미한다.
adj[i] : i번째 노드에 연결된 노드들을 원소로 갖는 리스트
인접 리스트 또한 무향 그래프의 경우에는 본인 노드 인덱스의 리스트 내에 서로를 원소로 갖게 된다.
인접 리스트의 장단점은?
인접 리스트를 활용하여 그래프의 연결 관계를 저장할 경우, 인접 리스트는 인접 행렬과 달리 실제로 연결된 노드에 대한 정보만 저장하기 때문에, 모든 벡터들의 원소의 개수의 합이 간선의 개수와 동일한다는 점이 있다. 즉, 간선의 개수에 비례하는 메모리만 차지하여 구현이 가능하다. 따라서 인접 행렬이 갖는 탐색의 비효율성을 인접 리스트를 통해 극복이 가능하다. 하지만 인접 리스트 또한 단점이 존재한다. 만일 노드 i와 노드 j의 연결 여부를 알고 싶을 경우에는 어떻게 해야 할까? adj[i] 의 리스트를 순회하며 j 원소가 존재하는지 확인해야 한다. 이러한 경우 O(V)의 시간 복잡도를 갖게 된다. 인접 행렬은 adj[i][j]가 1인지 0인지만 확인하면 i와 v 노드의 연결 여부를 O(1) 시간복잡도를 통해 확인이 가능했었다. 이러한 단점이 있기 때문에, 문제의 상황에 따라 적절한 표현 방식을 이용하여 연결 관계를 저장하는 것이 매우 중요하다고 할 수 있다.
따라서 무방향 그래프일때 예시 코드는 다음과 같다.
#include <iostream>
using namespace std;
int n, m;
vector<int> adj[10];
int main() {
cin >> n >> m;
for (int i=0; i<n; i++) {
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
}📌 Kruskal Algorithm & Code
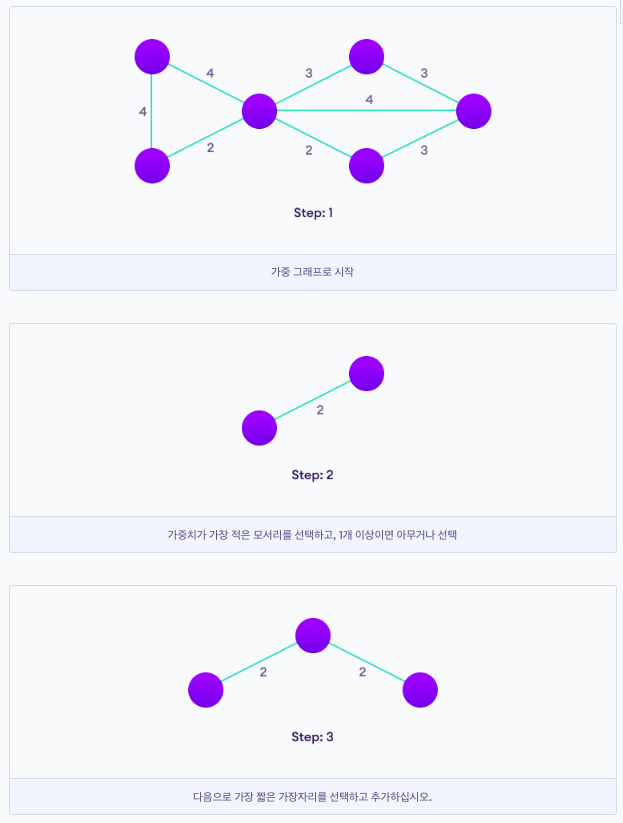
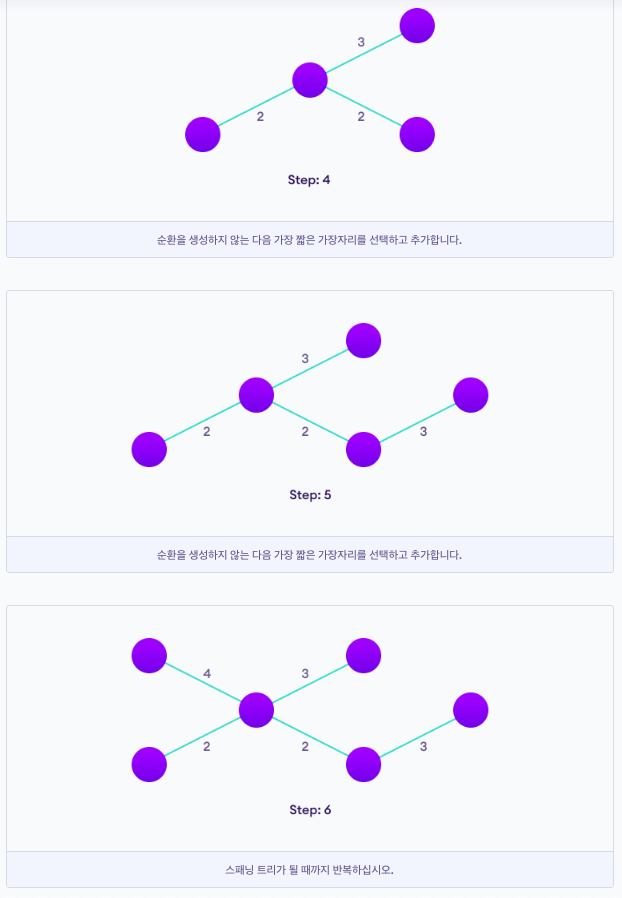
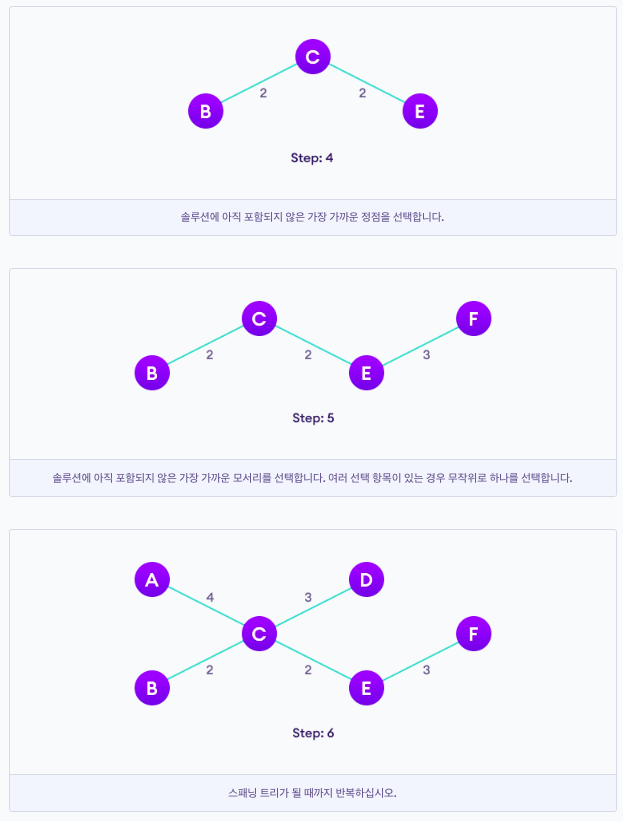
가중치가 가장 낮은 가장자리부터 시작하여 목표에 도달할 때까지 가장자리를 계속 추가한다. Kruskal 알고리즘을 구현하는 단계는 다음과 같다.
1. 모든 가장자리를 낮은 가중치에서 높은 가중치로 정렬
2. 가중치가 가장 낮은 간선을 가져와 스패닝 트리에 추가, 에지를 추가하여 주기가 생성된 경우 이 에지를 거부.
3. 모든 정점에 도달할 때까지 가장자리를 계속 추가.
<pseudo code>
KRUSKAL(G):
A = ∅
For each vertex v ∈ G.V:
MAKE-SET(v)
For each edge (u, v) ∈ G.E ordered by increasing order by weight(u, v):
if FIND-SET(u) ≠ FIND-SET(v):
A = A ∪ {(u, v)}
UNION(u, v)
return A// Kruskal's algorithm in C++
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
#define edge pair<int, int>
class Graph {
private:
vector<pair<int, edge> > G; // graph
vector<pair<int, edge> > T; // mst
int *parent;
int V; // number of vertices/nodes in graph
public:
Graph(int V);
void AddWeightedEdge(int u, int v, int w);
int find_set(int i);
void union_set(int u, int v);
void kruskal();
void print();
};
Graph::Graph(int V) {
parent = new int[V];
//i 0 1 2 3 4 5
//parent[i] 0 1 2 3 4 5
for (int i = 0; i < V; i++)
parent[i] = i;
G.clear();
T.clear();
}
void Graph::AddWeightedEdge(int u, int v, int w) {
G.push_back(make_pair(w, edge(u, v)));
}
int Graph::find_set(int i) {
// If i is the parent of itself
if (i == parent[i])
return i;
else
// Else if i is not the parent of itself
// Then i is not the representative of his set,
// so we recursively call Find on its parent
return find_set(parent[i]);
}
void Graph::union_set(int u, int v) {
parent[u] = parent[v];
}
void Graph::kruskal() {
int i, uRep, vRep;
sort(G.begin(), G.end()); // increasing weight
for (i = 0; i < G.size(); i++) {
uRep = find_set(G[i].second.first);
vRep = find_set(G[i].second.second);
if (uRep != vRep) {
T.push_back(G[i]); // add to tree
union_set(uRep, vRep);
}
}
}
void Graph::print() {
cout << "Edge :"
<< " Weight" << endl;
for (int i = 0; i < T.size(); i++) {
cout << T[i].second.first << " - " << T[i].second.second << " : "
<< T[i].first;
cout << endl;
}
}
int main() {
Graph g(6);
g.AddWeightedEdge(0, 1, 4);
g.AddWeightedEdge(0, 2, 4);
g.AddWeightedEdge(1, 2, 2);
g.AddWeightedEdge(1, 0, 4);
g.AddWeightedEdge(2, 0, 4);
g.AddWeightedEdge(2, 1, 2);
g.AddWeightedEdge(2, 3, 3);
g.AddWeightedEdge(2, 5, 2);
g.AddWeightedEdge(2, 4, 4);
g.AddWeightedEdge(3, 2, 3);
g.AddWeightedEdge(3, 4, 3);
g.AddWeightedEdge(4, 2, 4);
g.AddWeightedEdge(4, 3, 3);
g.AddWeightedEdge(5, 2, 2);
g.AddWeightedEdge(5, 4, 3);
g.kruskal();
g.print();
return 0;
}📌 Prim Algorithm & Code
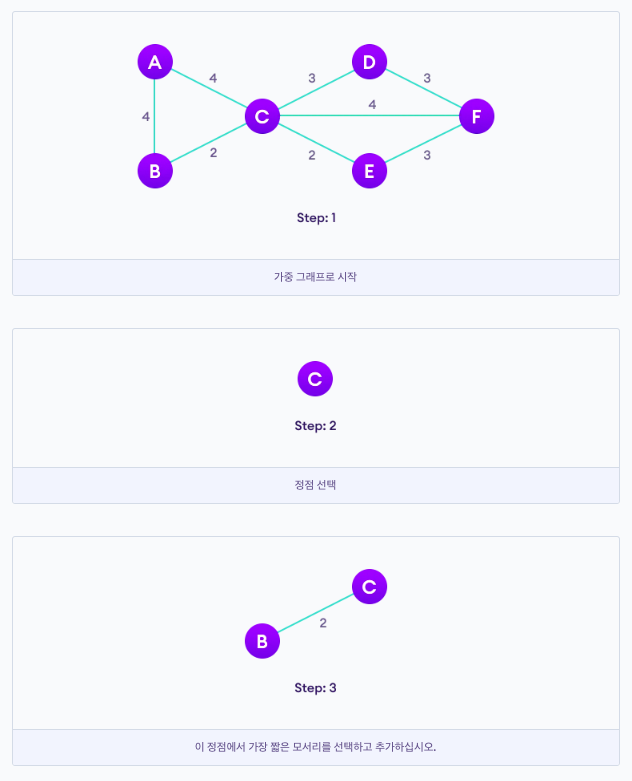
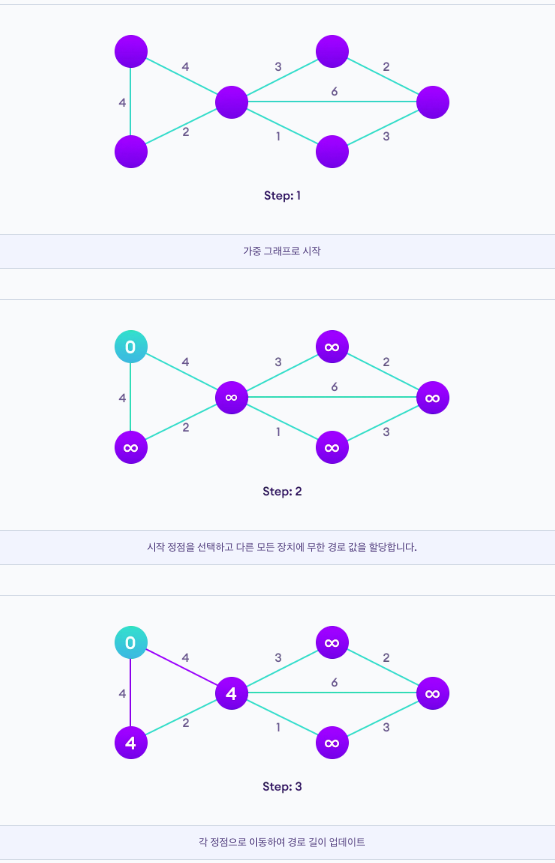
하나의 정점에서 시작하여 목표에 도달할 때까지 가중치가 가장 낮은 가장자리를 계속 추가한다. Prim의 알고리즘을 구현하는 단계는 다음과 같다.
1. 임의로 선택한 정점으로 최소 신장 트리를 초기화.
2. 트리를 새 정점에 연결하는 모든 가장자리를 찾고 최소값을 찾아 트리에 추가.
3. 최소 스패닝 트리를 얻을 때까지 2단계를 계속 반복.
<pseudo code>
T = ∅;
U = { 1 };
while (U ≠ V)
let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U;
T = T ∪ {(u, v)}
U = U ∪ {v}// Prim's Algorithm in C++
#include <cstring>
#include <iostream>
using namespace std;
#define INF 9999999
// number of vertices in grapj
#define V 5
// create a 2d array of size 5x5
//for adjacency matrix to represent graph
int G[V][V] = {
{0, 9, 75, 0, 0},
{9, 0, 95, 19, 42},
{75, 95, 0, 51, 66},
{0, 19, 51, 0, 31},
{0, 42, 66, 31, 0}};
int main() {
int no_edge; // number of edge
// create a array to track selected vertex
// selected will become true otherwise false
int selected[V];
// set selected false initially
memset(selected, false, sizeof(selected));
// set number of edge to 0
no_edge = 0;
// the number of egde in minimum spanning tree will be
// always less than (V -1), where V is number of vertices in
//graph
// choose 0th vertex and make it true
selected[0] = true;
int x; // row number
int y; // col number
// print for edge and weight
cout << "Edge"
<< " : "
<< "Weight";
cout << endl;
while (no_edge < V - 1) {
//For every vertex in the set S, find the all adjacent vertices
// , calculate the distance from the vertex selected at step 1.
// if the vertex is already in the set S, discard it otherwise
//choose another vertex nearest to selected vertex at step 1.
int min = INF;
x = 0;
y = 0;
for (int i = 0; i < V; i++) {
if (selected[i]) {
for (int j = 0; j < V; j++) {
if (!selected[j] && G[i][j]) { // not in selected and there is an edge
if (min > G[i][j]) {
min = G[i][j];
x = i;
y = j;
}
}
}
}
}
cout << x << " - " << y << " : " << G[x][y];
cout << endl;
selected[y] = true;
no_edge++;
}
return 0;
}📌 Dijkstra Algorithm & Code
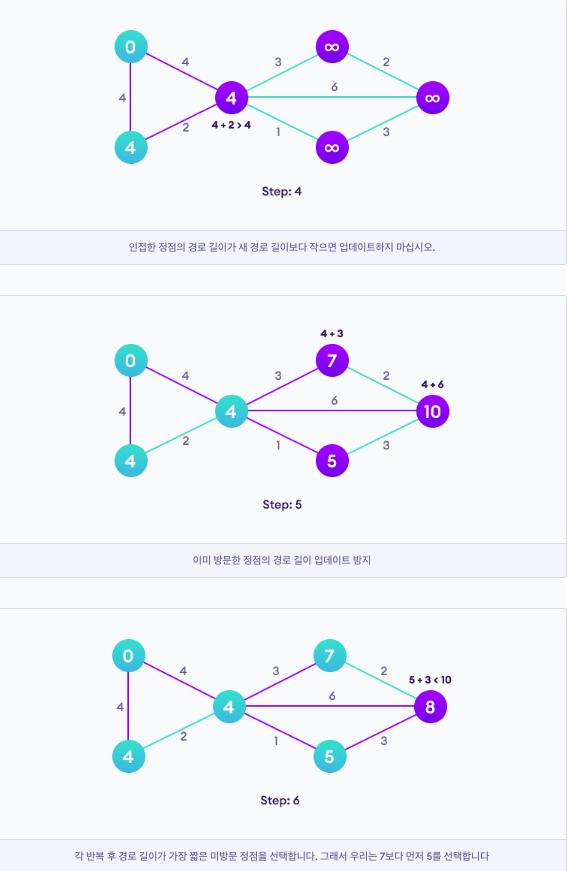
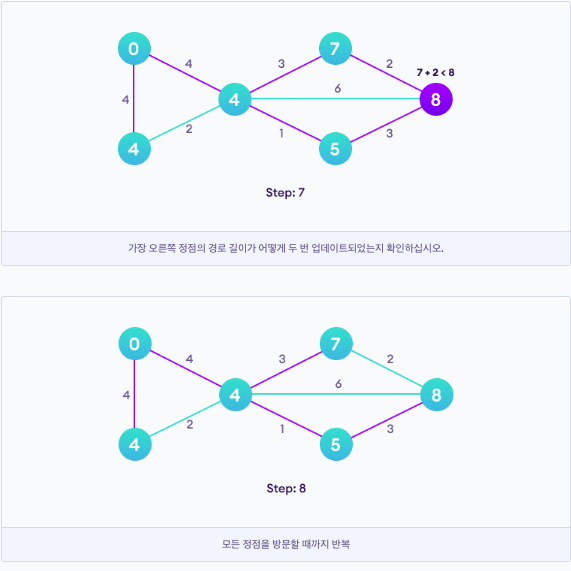
<pseudo code>
function dijkstra(G, S)
for each vertex V in G
distance[V] <- infinite
previous[V] <- NULL
If V != S, add V to Priority Queue Q
distance[S] <- 0
while Q IS NOT EMPTY
U <- Extract MIN from Q
for each unvisited neighbour V of U
tempDistance <- distance[U] + edge_weight(U, V)
if tempDistance < distance[V]
distance[V] <- tempDistance
previous[V] <- U
return distance[], previous[]// Dijkstra's Algorithm in C++
#include <iostream>
#include <vector>
#define INT_MAX 10000000
using namespace std;
void DijkstrasTest();
int main() {
DijkstrasTest();
return 0;
}
class Node;
class Edge;
void Dijkstras();
vector<Node*>* AdjacentRemainingNodes(Node* node);
Node* ExtractSmallest(vector<Node*>& nodes);
int Distance(Node* node1, Node* node2);
bool Contains(vector<Node*>& nodes, Node* node);
void PrintShortestRouteTo(Node* destination);
vector<Node*> nodes;
vector<Edge*> edges;
class Node {
public:
Node(char id)
: id(id), previous(NULL), distanceFromStart(INT_MAX) {
nodes.push_back(this);
}
public:
char id;
Node* previous;
int distanceFromStart;
};
class Edge {
public:
Edge(Node* node1, Node* node2, int distance)
: node1(node1), node2(node2), distance(distance) {
edges.push_back(this);
}
bool Connects(Node* node1, Node* node2) {
return (
(node1 == this->node1 &&
node2 == this->node2) ||
(node1 == this->node2 &&
node2 == this->node1));
}
public:
Node* node1;
Node* node2;
int distance;
};
///////////////////
void DijkstrasTest() {
Node* a = new Node('a');
Node* b = new Node('b');
Node* c = new Node('c');
Node* d = new Node('d');
Node* e = new Node('e');
Node* f = new Node('f');
Node* g = new Node('g');
Edge* e1 = new Edge(a, c, 1);
Edge* e2 = new Edge(a, d, 2);
Edge* e3 = new Edge(b, c, 2);
Edge* e4 = new Edge(c, d, 1);
Edge* e5 = new Edge(b, f, 3);
Edge* e6 = new Edge(c, e, 3);
Edge* e7 = new Edge(e, f, 2);
Edge* e8 = new Edge(d, g, 1);
Edge* e9 = new Edge(g, f, 1);
a->distanceFromStart = 0; // set start node
Dijkstras();
PrintShortestRouteTo(f);
}
///////////////////
void Dijkstras() {
while (nodes.size() > 0) {
Node* smallest = ExtractSmallest(nodes);
vector<Node*>* adjacentNodes =
AdjacentRemainingNodes(smallest);
const int size = adjacentNodes->size();
for (int i = 0; i < size; ++i) {
Node* adjacent = adjacentNodes->at(i);
int distance = Distance(smallest, adjacent) +
smallest->distanceFromStart;
if (distance < adjacent->distanceFromStart) {
adjacent->distanceFromStart = distance;
adjacent->previous = smallest;
}
}
delete adjacentNodes;
}
}
// Find the node with the smallest distance,
// remove it, and return it.
Node* ExtractSmallest(vector<Node*>& nodes) {
int size = nodes.size();
if (size == 0) return NULL;
int smallestPosition = 0;
Node* smallest = nodes.at(0);
for (int i = 1; i < size; ++i) {
Node* current = nodes.at(i);
if (current->distanceFromStart <
smallest->distanceFromStart) {
smallest = current;
smallestPosition = i;
}
}
nodes.erase(nodes.begin() + smallestPosition);
return smallest;
}
// Return all nodes adjacent to 'node' which are still
// in the 'nodes' collection.
vector<Node*>* AdjacentRemainingNodes(Node* node) {
vector<Node*>* adjacentNodes = new vector<Node*>();
const int size = edges.size();
for (int i = 0; i < size; ++i) {
Edge* edge = edges.at(i);
Node* adjacent = NULL;
if (edge->node1 == node) {
adjacent = edge->node2;
} else if (edge->node2 == node) {
adjacent = edge->node1;
}
if (adjacent && Contains(nodes, adjacent)) {
adjacentNodes->push_back(adjacent);
}
}
return adjacentNodes;
}
// Return distance between two connected nodes
int Distance(Node* node1, Node* node2) {
const int size = edges.size();
for (int i = 0; i < size; ++i) {
Edge* edge = edges.at(i);
if (edge->Connects(node1, node2)) {
return edge->distance;
}
}
return -1; // should never happen
}
// Does the 'nodes' vector contain 'node'
bool Contains(vector<Node*>& nodes, Node* node) {
const int size = nodes.size();
for (int i = 0; i < size; ++i) {
if (node == nodes.at(i)) {
return true;
}
}
return false;
}
///////////////////
void PrintShortestRouteTo(Node* destination) {
Node* previous = destination;
cout << "Distance from start: "
<< destination->distanceFromStart << endl;
while (previous) {
cout << previous->id << " ";
previous = previous->previous;
}
cout << endl;
}
// these two not needed
vector<Edge*>* AdjacentEdges(vector<Edge*>& Edges, Node* node);
void RemoveEdge(vector<Edge*>& Edges, Edge* edge);
vector<Edge*>* AdjacentEdges(vector<Edge*>& edges, Node* node) {
vector<Edge*>* adjacentEdges = new vector<Edge*>();
const int size = edges.size();
for (int i = 0; i < size; ++i) {
Edge* edge = edges.at(i);
if (edge->node1 == node) {
cout << "adjacent: " << edge->node2->id << endl;
adjacentEdges->push_back(edge);
} else if (edge->node2 == node) {
cout << "adjacent: " << edge->node1->id << endl;
adjacentEdges->push_back(edge);
}
}
return adjacentEdges;
}
void RemoveEdge(vector<Edge*>& edges, Edge* edge) {
vector<Edge*>::iterator it;
for (it = edges.begin(); it < edges.end(); ++it) {
if (*it == edge) {
edges.erase(it);
return;
}
}
}