1. Rank를 Code로 구현...?

나는 "Rank란, BST 응용에 사용되는 것으로써, 스케줄링 상황이라고 생각할 수 있다. 예를 들면, 가게에서 손님이 도착을 하기전에 그동안 만들어놓은 요리가 총 몇 개인지를 물어봤을 때와 같은 상황을 말한다."고 생각했다.

그러나... 위와 같은 구체적인 상황에서 Rank를 Code로 구현하는 것을 상상해보아도 많이 막연해서 완벽한 코드 구현이 어려울 것 같다는 판단이 들었다. 이 부분은 추후 수업을 좀 더 들어보고 구현할 수 있을때 구현하려고 한다.

2. AVL Tree란?

Adeleson-Velskii와 Landis에 의해 제한된 트리라 AVL 트리이다.

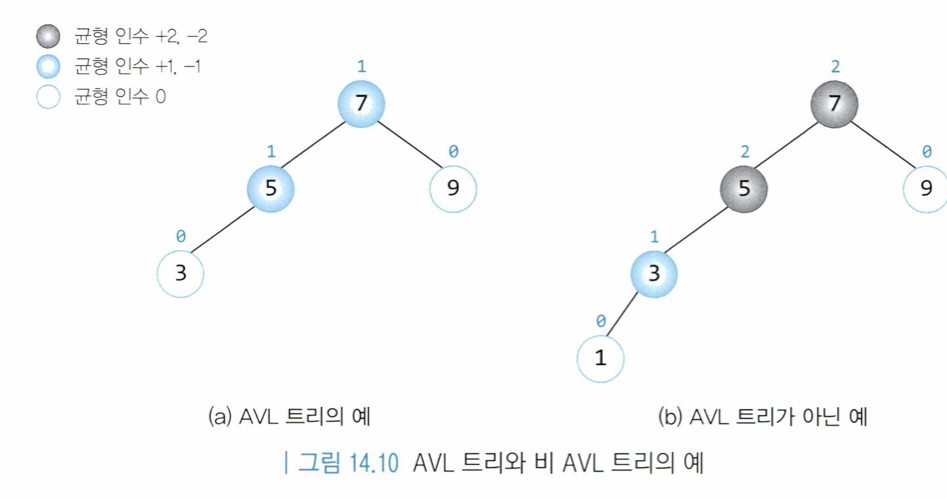
각 노드에서 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가 1 이하인 이진 탐색 트리를 말한다.

예시는 아래와 같다.

여기서 균형 인수라는 단어가 나오는데, 균형 인수(Balance Factor)란, (왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이)이다.

이 얘기를 들으면 바로 이 자료의 모든 것이 이해가 갈 것이다.

이 트리는 트리가 비균형 상태로 되면 스스로 노드들을 재배치하여 균형 상태로 만든다. 높이가 높아지면 시간복잡도가 증가하여 BST를 사용하는 이유가 없어지기 때문에 균형화를 통해 높이를 최대한 낮추는 것이 AVL 트리이다. AVL트리는 항상 균형 트리를 보장하기 때문에 O(log n)의 탐색 시간을 보장한다. 삽입과 삭제 연산도 O(log n)에 포함된다.

(이에 대한 증명은 https://jihunlee25.tistory.com/19 이분의 블로그를 참고하면 좋을 것 같다. 너무 감사합니다.)

탐색의 경우 : AVL 트리도 탐색에서는 일반 이진 탐색 트리의 탐색 연산과 동일하며, 시간 복잡도도 O(log 2 n)으로 동일하다. AVL 트리에서 균형이 깨질 수 있는 연산은 삽입과 삭제 연산이다.

이에 대한, 그리고 삽입-회전에 자세한 얘기는 글이 너무 길어질 것 같아 추가로 공부한 후 다음 게시글에서 다뤄볼 예정이다.
(+개인적으로 박람회를 다녀온 내용도 함께 올리려 한다.)
(++또한 글을 작성하며 이진트리vs이진탐색트리, 이진탐색vs이진탐색트리에 대한 개념이 아주 살짝 헷갈리는 경험을 하였다. 이에 대한 내용도 새로운 글로 다룰 것이다.)

3. AVL Tree Code로 구현

아직 회전에 대한 자세한 내용은 다루지 않았지만 어느 정도는 알아야 코드에 대한 이해가 가능하기 때문에 개념을 요약해서 올려놓는다.

AVL 트리의 삽입 연산

-삽입된 노드 N으로부터 가장 가까우면서 균형 인수가 ±2가 된 조상 노드가 A라면

• LL 타입: N이 A의 왼쪽서브트리의 왼쪽서브트리에 삽입
• LR 타입: N이 A의 왼쪽서브트리의 오른쪽서브트리에 삽입
• RR 타입: N이 A의 오른쪽서브트리의 오른쪽서브트리에 삽입
• RL 타입: N이 A의 오른쪽서브트리의 왼쪽서브트리에 삽입

-각 타입별 재균형 방법

• LL 회전: A부터 N까지의 경로상 노드의 오른쪽 회전
• LR 회전: A부터 N까지의 경로상 노드의 왼쪽-오른쪽 회전
• RR 회전: A부터 N까지의 경로상 노드의 왼쪽 회전
• RL 회전: A부터 N까지의 경로상 노드의 오른쪽-왼쪽 회전

이제 코드를 소개한다. 이 코드를 통해 대략적인 개요를 이해하면 좋을 것 같다.

이진 탐색 트리 클래스를 상속한 AVL 트리 클래스 Code

#include <iostream>
using namespace std;

// AVLTree.h: AVL 트리 클래스 CAVLTree
#include "BinSrchTree.h"
class AVLTree : public BinSrchTree {
public : 
			// 노드의 균형인수를 qksghks
            int getHeightDiff(BinaryNode *node) {
            	if( node==NULL )
                	return 0;
                int hLeft = getHeight(node -> getLeft());
                int hRight = getHeight(node -> getRight());
                return hLeft - hRight;
            }
            // LL 회전 함수
            BinaryNode *rotateLL(BinaryNode* parent) {
				BinaryNode* child = parent -> getLeft();
                child -> setRight (parent);
                return child;
            }
            // RR 회전 함수
            BinaryNode *rotateRR(BinaryNode* parent) {
				BinaryNode* child = parent -> getRight();
                parent -> setRight(child -> getLeft());
                child -> setLeft(parent);
                return child;
            }
            // RL 회전 함수
            BinaryNode *rotateRR(BinaryNode* parent) {
				BinaryNode* child = parent -> getRight();
                parent -> setRight (rotateLL(child));
                return rotateRR(parent);
            // LR 회전 함수
            BinaryNode *rotateLR(BinaryNode* parent) {
				BinaryNode* child = parent -> getLeft();
                parent -> setLeft (rotateRR(child));
                return rotateLL(parent);
            // 트리를 균형트리로 만든다
            BinaryNode *reBalance (BinaryNode *parent) {
            	int hDiff = getHeightDiff(parent);
                if ( hDiff > 1) {
                	if ( getHeightDiff(parent -> getLeft() > 0 )
                    	parent = rotateLL( parent );
                    else parent = retateLR( parent );
                else if ( hDiff < -1 ) {
                	if ( getHeightDiff ( parent -> getRight() ) < 0 )
                    	parent = rotateRR ( parent );
                    else parent = rotateRL ( parent );
                }
                return parent;
                // AVL 트리의 삽입 연산
                void insert( int data ) {
                	if (isEmpty()) root = new BinaryNode ( data );
                    else root = insertAVL ( root, data );
                    }
                BinaryNode* insertAVL(BinaryNode* parent, int data) {
                	if ( data < parent -> getData() ) {
						if ( parent -> getLeft() != NULL )
                        	 parent -> setLeft(insertAVL(parent -> getLeft(), data));
                        else parent -> setLeft ( new BinaryNode(data) );
                        return reBalance(parent);
                    }
                    else if ( data > parent -> getData() ) {
						if ( parent -> getRight() != NULL )
                        	 parent -> setRight(insertAVL(parent -> getRight(), data));
                        else parent -> setRight ( new BinaryNode(data) );
                        return reBalance(parent);
                    }
                    else {
							printf("중복된 키 에러\n");
                            return NULL;
                    }
          }
};

코드 설명
3행 : BinSrchTree 클래스를 상속해서 AVL 트리 클래서 AVLTree를 선언함.
7~12행 : getHeightDiff() 노드의 균형 인수를 반환하는 함수. 좌우 서브트리의 높이를 구해 차를 반환.
40~53행 reBalance() : 트리를 균형 상태로 만들어 주는 함수. 먼저 양쪽 서브 트리의 높이의 차이를 구한 다음, 왼쪽 서브트리가 더 높으면 왼쪽 서브트리의 높이의 차이를 다시 구함. 여기에 따라서 LL회전인지, LR회전인지를 결정하고 해당하는 함수를 호출. 오른쪽 서브트리가 더 높은 경우에도 마찬가지로, 오른쪽 서브트리의 높이의 차이를 구하여 RR회전인지, RL회전인지를 결정함.
59~78행 indertAVL() : 삽입함수. parent가 현재 노드와 같은 키를 가지면 에러를 출력하고 바로 반환. parent가 왼쪽 자식으로 가야하는 경우에 왼쪽 자식이 없는 경우는 바로 왼쪽 자식으로 설정해주면 되지만 그렇지 않은 경우 왼쪽 자식 노드에게 삽입 역할을 넘김. 주의할 점은 왼쪽 서브트리에 삽입된 후 왼쪽 자식이 변경될 수도 있고, 따라서 반환 값으로 parent의 왼쪽 자식을 재설정해야 함. 오른쪽으로 추가하는 경우도 마찬가지임. 노드를 삽입하고 나면 균형 인수가 변경될 수 있으므로 reBalance() 함수를 실행해서 다시 균형을 잡음.

이렇게 글을 마친다. : )
*이 책은 천인국 외 1명의 저자가 작성한 C++로 쉽게 풀어쓴 자료구조 책을 참고하였습니다. 감사합니다.