😊 잠시 알아둬야 할 점! 😊

그래프 탐색이란, 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것을 말합니다.

📌 1. BFS란? (BFS 알고리즘을 사용한 그래프 탐색 과정 & Code)

BFS란?

너비우선탐색(Breadth-First Search)을 말합니다.
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법입니다.

사용하는 경우?

두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 사용합니다.

사용하는 자료구조?

방문한 노드들을 차례로 저장한 후 방문해야 하기 때문에, 꺼낼 수 있는 자료 구조인 큐(Queue)를 사용합니다. FIFO 원칙으로 탐색합니다.

BFS는 직접 그래프를 탐색하면서 보는 것이 이해가 빠릅니다. 직접 그려봤습니다.

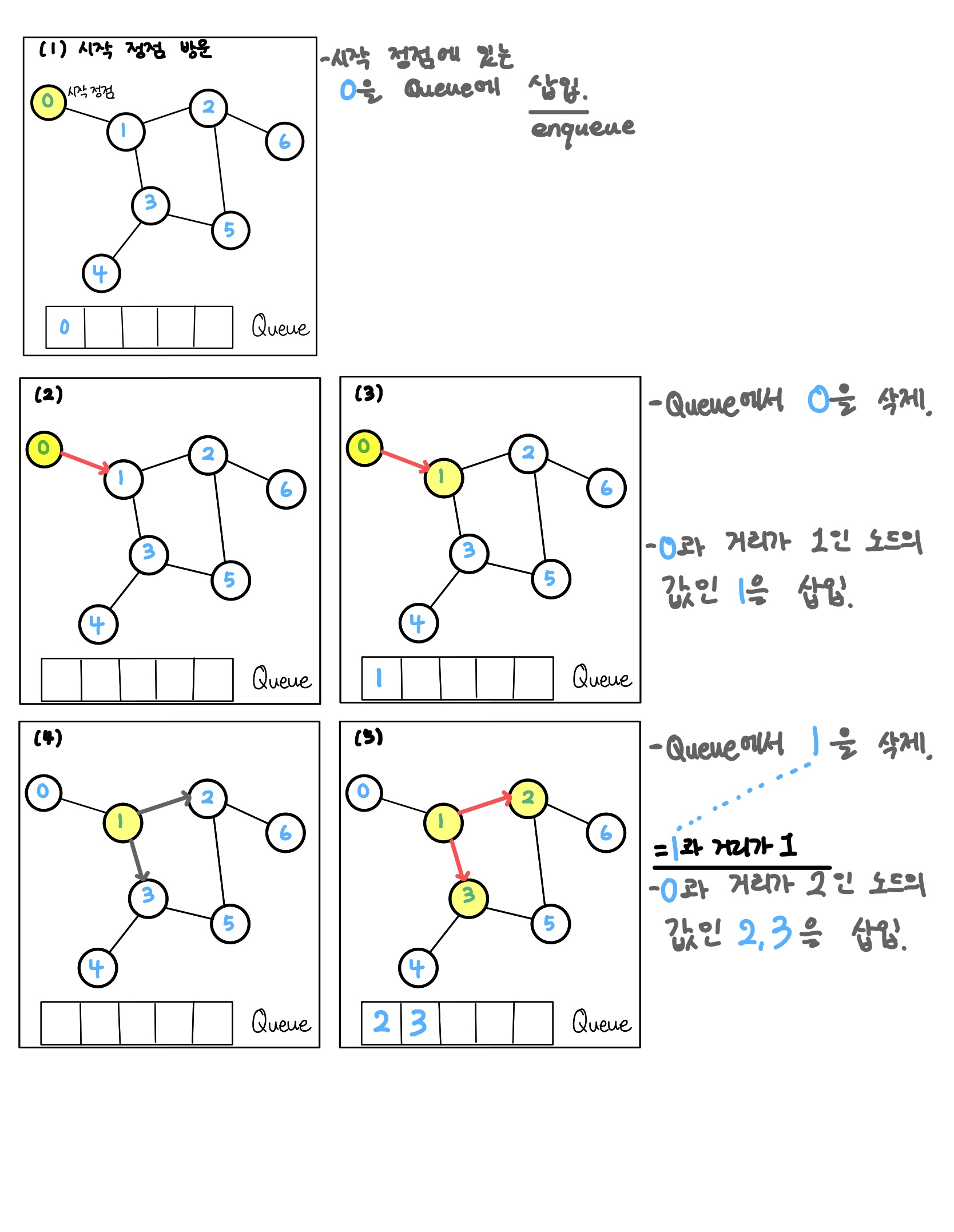
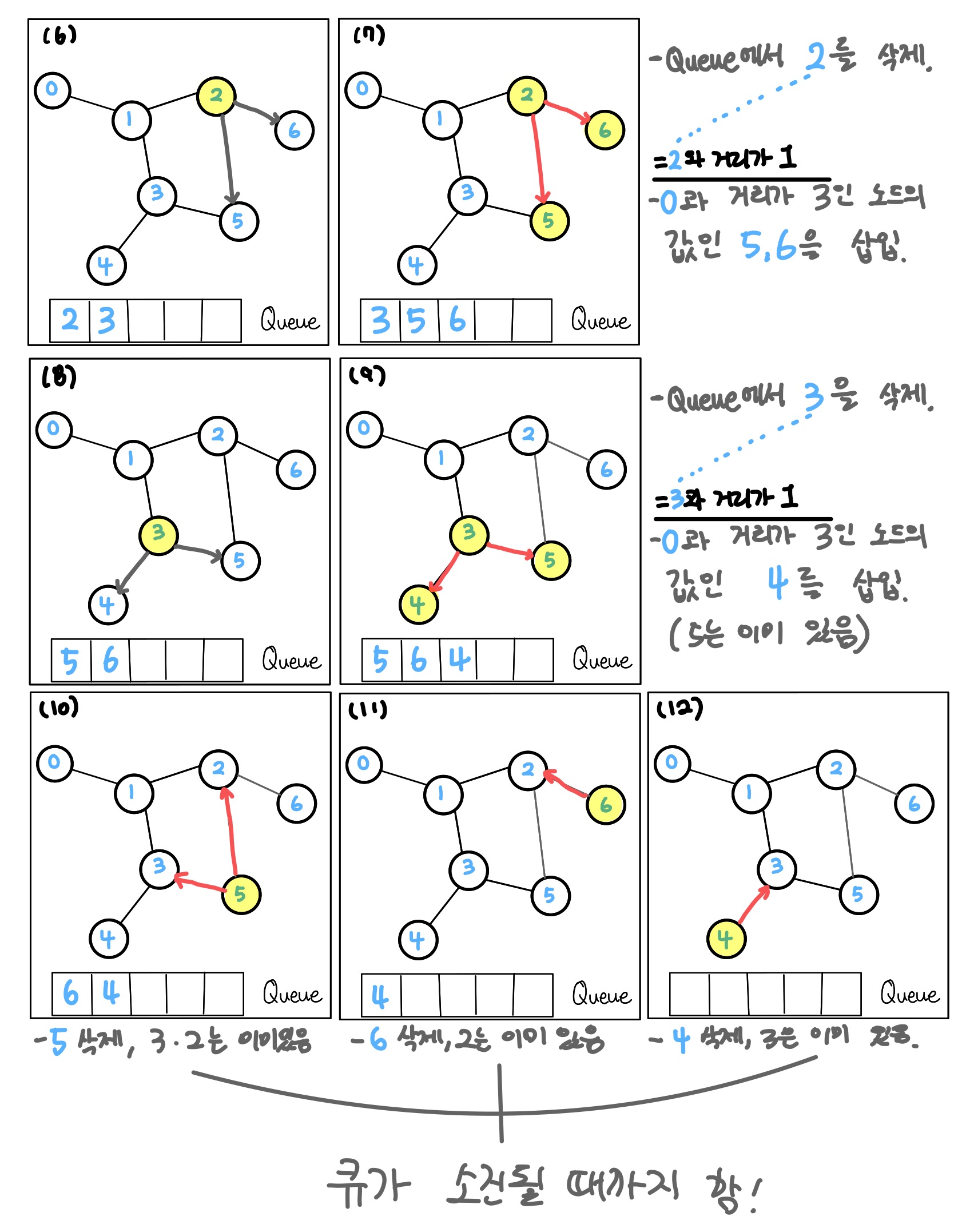
이렇게 BFS의 탐색 과정이 끝났습니다. 이제 Code로 변환할 차례입니다.
바로 Code로 변환하면 제 머리가 터질 것 같으니...
간략하게 글로 코드 개요를 먼저 작성해보겠습니다.

breadthFirstSearch(v)

	v를 방문되었다고 표시;
    큐 Q에 정점 v를 삽입;
    while (not is_empty(Q)) do
    	Q에서 정점 W를 삭제;
        for all u ∈ (W에 인접한 정점) do
        	if (u가 아직 방문되지 않았으면)
             	then u를 큐에 삽입;
                	u를 방문되었다고 표시;    

이제 아래처럼 코드를 작성할 수 있습니다.

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

bool visited[7];
vector<int> graph[7];

// BFS 함수 정의
void bfs(int start) {
    queue<int> q;
    q.push(start); // 첫 노드를 queue에 삽입
    visited[start] = true; // 첫 노드를 방문되었다고 표시

    // 큐가 빌 때까지 반복
    while (!q.empty()) {
        // 큐에서 하나의 원소를 뽑아 출력 및 삭제
        int x = q.front();
        q.pop();
        cout << x << ' ';
        // 해당 원소와 인접한 정점 중, 아직 방문하지 않은 원소들을 큐에 삽입, 방문되었다고 표시
        for (int i = 0; i < graph[x].size(); i++) {
            int y = graph[x][i];
            if (!visited[y]) {
                q.push(y);
                visited[y] = true;
            }
        }
    }
}

//그래프 만들기
int main(void)
{
    graph[0].push_back(1);
    graph[1].push_back(2);
    graph[1].push_back(3);
    graph[2].push_back(5);
    graph[2].push_back(6);
    graph[3].push_back(4);
    graph[3].push_back(5);

    bfs(0);
}

결과는 아래와 같이 우리가 그림에서 본 결과와 똑같이 나왔습니다.
(환경이 mac으로 바뀌어서 아직 세팅이 덜 되어서 잠시 웹 컴파일러를 사용했습니다.)

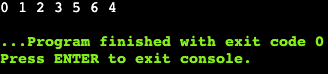
📌 2. DFS란? (DFS 알고리즘을 사용한 그래프 탐색 과정 & Code)

DFS란?

깊이우선탐색(Depth-First Search)을 말합니다.
시작 정점으로부터 한 루트로 탐색하다가 특정 상황에서 최대한 깊숙이 들어가서 확인한 뒤 다시 돌아가 다른 루트로 탐색하는 방식입니다.

사용하는 경우?

모든 노드를 방문 하고자 하는 경우에 이 방법을 사용합니다 예시로는 자동 미로 생성에 많이 사용되는 알고리즘입니다.

사용하는 자료구조?

깊이 우선 탐색은 스택(Stack)을 이용해서 구현한다. 또한, 컴퓨터는 구조적으로 함수를 호출할 때 스택의 원리를 이용하기 때문에 스택을 선언하여 사용하지 않고 재귀적 함수 호출로 구현할 수도 있습니다. LIFO 방식입니다.

DFS도 직접 그래프를 탐색하면서 보는 것이 이해가 빠릅니다.
이번에는.. 위 그림을 그리느라 힘을 다 빼기도 했고.. 인터넷에 좋은 그림이 있어 참고해봤습니다.

이분 링크를 참고했습니다. 감사합니다.

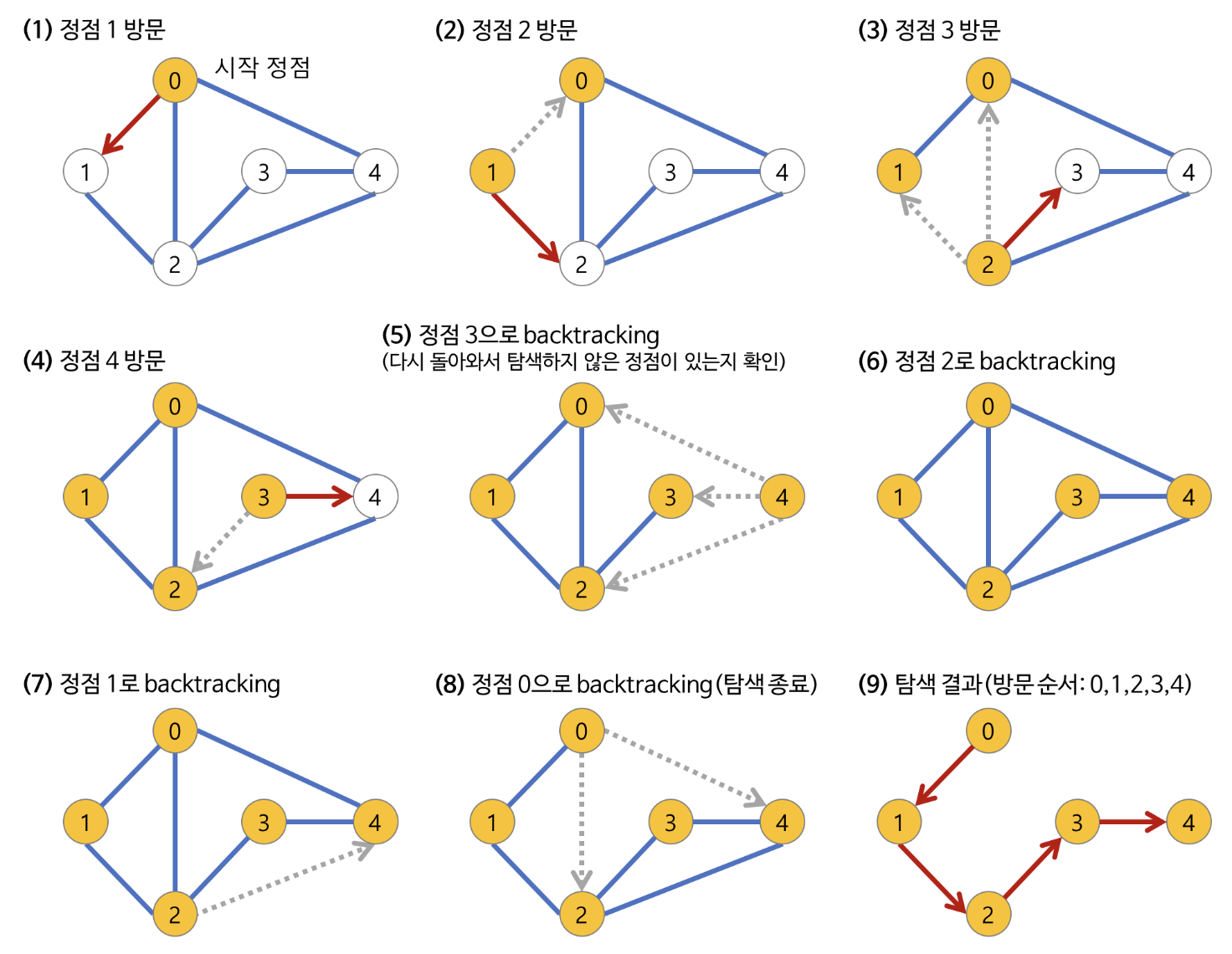
이제 pseudo 코드를 볼 차례입니다.

depthFirstSearch(v)

	v를 방문되었다고 표시;
    for all u ∈ (v에 인접한 정점) do
    	if (u가 아직 방문되지 않았으면)
        	then depthFirstSearch(u)

이제 실제 code를 보겠습니다.

#include <iostream>
#include <vector>
using namespace std;

bool visited[5]; 
vector<int> graph[5];

void dfs(int x)
{
	visited[x] = true;
	cout << x << " ";
	for (int i = 0; i < graph[x].size(); i++) // 인접한 노드 사이즈만큼 탐색
	{
		int y = graph[x][i];
		if (!visited[y]) // 방문하지 않았으면 즉 visited가 False일 때 not을 해주면 True가 되므로 아래 dfs 실행
            dfs(y); // 재귀적으로 방문
	}
}

int main(void)
{
    graph[0].push_back(1);
    graph[1].push_back(2);
    graph[2].push_back(3);
	graph[2].push_back(4);
	graph[3].push_back(4);
        
    dfs(0);
}

이 친구도 결과가 잘 나옵니다.

📌 3. BFS vs DFS

geeksforgeeks를 참고하여 보기 좋게 아래에 표로 정리해봤습니다.

	BFS	DFS
뜻	Breadth First Search	Depth First Search
데이터 구조	Queue	Stack
정의	다음 레벨로 이동하기 전에 동일한 레벨의 모든 노드를 먼저 살펴보는 순회 접근 방식	탐색이 루트 노드에서 시작하여 방문하지 않은 근처 노드가 없는 노드에 도달할 때까지 노드를 최대한 멀리 진행하는 탐색 접근 방식
기술	가중치가 없는 그래프에서 단일 소스 최단 경로를 찾는 데 사용할 수 있음, 소스 정점에서 최소 수의 가장자리를 가진 정점에 도달하기 때문	소스에서 대상 정점에 도달하기 위해 더 많은 가장자리를 통과할 수 있음
개념적 차이	레벨별로 트리를 빌드	하위 트리별로 트리의 하위 트리를 빌드
접근 방식	FIFO	LIFO
사용	주어진 소스에 더 가까운 정점을 검색하는데 적합	솔루션이 소스에서 멀리 떨어져 있을 때 더 적합
의사 결정 트리에서의 적합성	모든 이웃을 먼저 고려하므로 게임이나 퍼즐에 사용되는 의사 결정 트리에는 적합하지 않음	게임이나 퍼즐 문제에 더 적합, 우리는 결정을 내리고 결정을 통해 모든 경로를 탐색, 결정이 승리상황으로 이어지면 중단.
시간 복잡도	Adj List를 사용할때 O(V+E)이고 Adj Matrix를 사용할 때 O(V^2), V는 정점, E는 가장자리	Adj List를 사용할때 O(V+E)이고 Adj Matrix를 사용할 때 O(V^2), V는 정점, E는 가장자리(동일함)
순회노드제거	여러 번 순회하는 노드는 대기열에서 삭제됨	방문한 노드는 스택에 추가된 다음 방문할 노드가 더 이상 없을 때 제거됨
역추적	역추적이라는 개념 없음	DFS 알고리즘은 역추적 개념을 사용하는 재귀 알고리즘
응용	이분 그래프, 최단 경로 등과 같은 다양한 응용 프로그램	순환 그래프 및 토폴로지 순서 등과 같은 다양한 응용 프로그램
필요한 메모리 크기	더 많은 메모리가 필요	더 적은 메모리를 필요
최단 경로 최적성	최단 경로를 찾는 데 최적	최단 경로를 찾는 데 최적이 아님
공간 복잡성	공간 복잡도는 시간 복잡도에 비해 더 중요	한 번에 루트에서 리프 노드까지 단일 경로만 저장하면 되므로 공간 복잡성이 더 적음
속도	BFS는 DFS에 비해 느림	DFS는 BFS에 비해 빠름
사용하는 때?	대상이 소스에 가까울 때	대상이 소스에서 멀리 떨어져 있을 때

📌 +. BFS 관련 문제

백준 1260번 문제를 풀어봤습니다.

코드는 아래와 같습니다.

#include <iostream>
#include <queue>
using namespace std;
#define MAX 1001
 
int N, M, V; //정점개수, 간선개수, 시작정점
int map[MAX][MAX]; //인접 행렬 그래프
bool visited[MAX]; //정점 방문 여부
queue<int> q;
 
void reset() {
    for (int i = 1; i <= N; i++) {
        visited[i] = 0;
    }
}
 
void DFS(int v) {
    visited[v] = true;
    cout << v << " ";
    
    for (int i = 1; i <= N; i++) {
        if (map[v][i] == 1 && visited[i] == 0) { //현재 정점과 연결되어있고 방문되지 않았으면
            DFS(i);
        }
    }
}
 
void BFS(int v) {
    q.push(v);
    visited[v] = true;
    cout << v << " ";
 
    while (!q.empty()) {
        v = q.front();
        q.pop();
        
        for (int w = 1; w <= N; w++) {
            if (map[v][w] == 1 && visited[w] == 0) { //현재 정점과 연결되어있고 방문되지 않았으면
                q.push(w);
                visited[w] = true;
                cout << w << " ";
            }
        }
    }
}
 
int main() {
    cin >> N >> M >> V;
 
    for (int i = 0; i < M; i++) {
        int a, b;
        cin >> a >> b;
        map[a][b] = 1;
        map[b][a] = 1;
    }
 
    reset();
    DFS(V);
    
    cout << '\n';
    
    reset();
    BFS(V);
 
    return 0;
}