Attention, Transformer(Self-Attention)

DONGJIN IM·2022년 3월 7일

AI 이론

AI(NLP) 이론

목록 보기

16/18

https://nlpinkorean.github.io/illustrated-transformer/
- Transformer에 대한 정리가 잘 되어 있기 때문에 꼭 참조하기를 추천!

Attention

Seq2Seq

Many-to-Many RNN type
Encoder와 Decoder를 활용하여 문장을 다른 문장으로 바꾸는 Task
- 주로 Machine Translation Task에 자주 활용됨
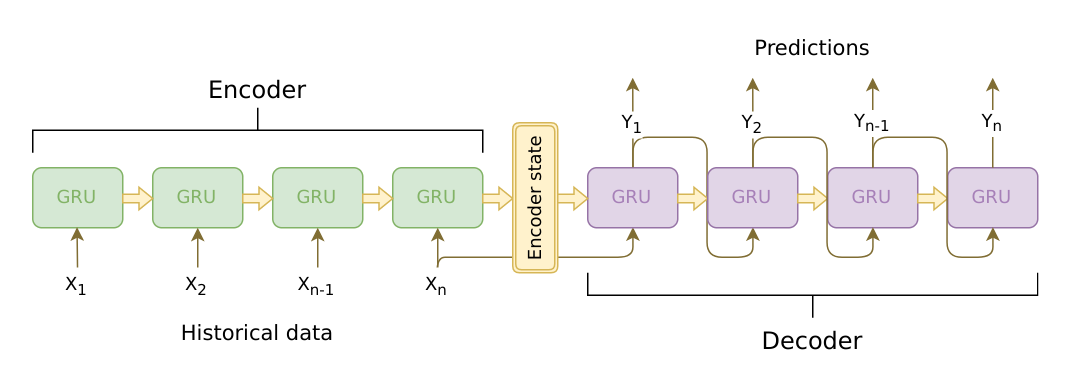
Encoder와 Decoder에 LSTM(혹은 GRU)를 적용한 기법
Encoder의 마지막 Model에서 반환된 Hidden State Vector와 Cell State를 그대로 Decoder의 첫번째 Model의 Input으로 활용
문제점
- 위에서 말했듯 Encoder의 마지막 Hidden state가 Decoder의 초기 hidden state로 사용이 됨
- 만약 Encoder의 Sequence Data 길이가 길 경우, Encoder 초기에 Input 값으로 들어온 단어의 정보가 거의 없어질 수 있다.
- 위 사진을 예로 들면, n = 100이라고 가정하자. Encoder State는 $x_1$ ~ $x_n$ 까지 LSTM을 거쳐 얻어진 Cell State와 Hidden State Vector가 저장되어 있고, 이렇게 저장된 값들을 활용하여 Decoder에서는 Prediction 과정이 수행될 것이다. 그런데, n이 너무 크기 때문에 $x_1$ 에 대한 정보가 Encoder State에서는 없어질(소실될) 가능성이 존재한다. 그리고 이런 문제는 번역 과정에서는 매우 치명적이다.
- 이런 문제를 해결하기 위해 문장을 거꾸로 하여 Input으로 다시 집어넣는 방법도 존재하였지만, Attention이라는 새로운 개념을 도입하여 해결하였다.

Attention이란?

Decoder에서 출력 단어를 예측하는 시점마다 Encoder에서의 전체 입력 문장을 다시 한 번 참고하는 것
- 해당 단어와 연관이 있는 단어를 좀 더 집중(Attention)하여 보게 됨

Attention 특징

NMT Performance를 향상시킴
- NMT : 기계 번역
Bottleneck Problem 해결
- 원래 존재하던 Seq2Seq Model에서는 Encoder의 마지막 Time Step의 Hidden State Vector만 활용해야 하므로, 초기 정보가 손실될 수 있다는 문제를 해결
- Encoder의 모든 단어에 대해 Hidden State Vector를 구하고, 이렇게 구한 모든 Hidden State Vector를 Decoder 연산에 활용하므로 생기는 장점
Gradient Vanishing Problem 해결
- BPTT를 수행할 때, Decoder의 Output부터 Encoder의 초기 부분까지 과정을 거치며 학습을 진행하는 것이 아니라 Attention Score를 통해 연산한 Atttention Output을 활용한 Path를 거쳐 학습이 진행되기 때문에 어떠한 Time Step도 거치지 않고 빠르고 변형 없이 값을 전달해 줄 수 있음
- Encoder 3개, Decoder가 3개 Layer로 존재한다고 가정하자. 만약 Attention이 아니라면 3번째 Decoder는 첫번째 Encoder에 중간 4개(2개 Decoder, 2개 Encoder) Layer를 거쳐 오차 값을 전달해 줄 것이다. 즉, 거치는 Path가 많아진다. 하지만 Attention은 Attention Score를 구할 때 3번째 Decoder의 Hidden State Vector와 첫번째 Encoder의 Hidden State Vector 연산이 수행되므로, BPTT 때 Attention Score를 구하는 과정의 Path를 역으로 활용하여 학습이 진행될 수 있다.
Interpretability 제공
- End-to-End 방식이므로, Alignment를 스스로 학습
  - Alighment : 원래의 문장에서, 대응하는 번역된 단어와 일치시키는 것
- Attention Distribution을 제공함으로써 단어의 분포(어느 단어에 집중하였는지)를 확인할 수 있다

Attention Mechanism

Dot\; : \;h_t^Th_s\newline General\; : \;h_t^TW_ah_s\newline concat\; : \;v_a^Ttanh(W_a[h_t;h_s])

Dot Product : 아래 자세히 설명
Generalized Dot Product
- Dot Product 사이에 특정 행렬을 추가시킴
- 중간 $W_a$ 행렬은 학습 가능한 행렬
- dot product와 General Product의 연산 결과는 Scalar 값이기 때문에,
  $W_a$ 의 형태는 아래와 같을 것이다.
  (Hidden State Vector Dimension) X (Hidden State Vector Dimension)
Concat
- Decoder Hidden State Vector와 Encoder의 Hidden State Vector(Q)를 Concat([ht;hs] 과정) 시키고, 이를 $W_a$ (가중치 행렬)와 곱하여 중간 Hidden Layer를 만듦.
  이후 Hidden Layer에 다시 $v_a^T$ 를 곱해주어 유사도를 나타낼 Scalar 값을 구함
- Layer를 2개 쌓아 학습이 진행되고, 최종적으로는 Scalar 값이 도출됨

Dot-Product Attention

가장 간단한 수식을 적용한 Attention
- 다른 Attention들은 Dot-Product 대신 다른 연산을 수행할 뿐 큰 차이는 없음
Attention Function : softmax( $QK^T$ )V = Attention Value
- Q : t 시점에서의 "Decoder Cell"에서의 Hidden State Vector
- K : 모든 시점에서의 "Encoder Cell"에서의 Hidden State Vector
- V : 모든 시점에서의 "Encoder Cell"에서의 Hidden State Vector

Attention 수행 순서

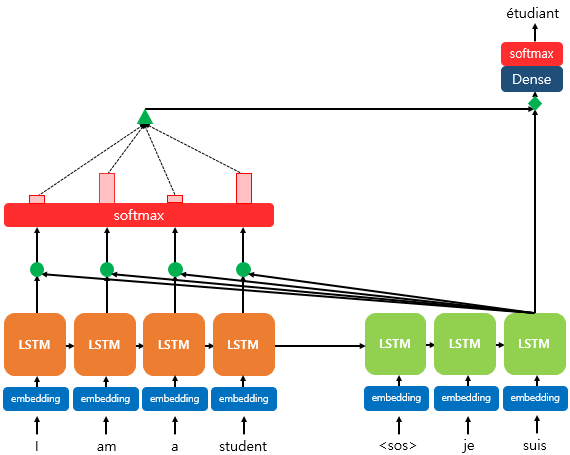
suis를 활용하여 etudiant라는 단어를 유추하는 사진
- suis에 관련된 K를 모든 Encoder 측 Input K를 활용하여 연산을 수행한다.
- 이후 softmax와 V를 활용하여 값을 도출하고, 이 값을 활용하여 다음 단어를 유추한다.
상세 과정

Attention Score 구하기
- Decoder Cell의 Hidden State Q와 Encoder Cell의 Hidden State인 K끼리 Dot Product 수행
- 현재 Decoder 시점 t에서 단어를 예측하기 위해 Encoder Cell에 존재하는 모든 단어에서 도출된 K와 전부 연산을 수행해야 함
Dot Product 연산을 softmax 함수에 넣어 Attention Distribution을 구함
Attention Distribution에 Encoder의 Hidden State(V)를 곱해주고, 이들을 모두 더하여 Attention Value(Context Vecotr)를 구함
Attention Value와 Decoder 중 현재 시점의 Hidden state cell을 Concatenate함
Vector를 가중치에 곱해주어 출력층 연산을 위한 Vector로 만들어줌
이전 과정에서 얻은 Vector를 Dense Layer를 거치고, softmax를 통과시키면 예측 벡터가 된다. 이 예측 벡터를 통해 다음 단어(사진에서는 etudiant)를 예측한다.
위 과정을 LSTM Model이 <EOS>(End of Sentence)를 반환할 때 까지 진행함

Transformer

Transformer란?

핵심 : Multi-Head Self-Attention을 활용해 Sequential Computation을 줄여 병렬 처리하는 부분을 늘려 더 많은 단어들 간의 Dependency를 모델링
Sequence Data를 다른 Type의 Sequence Data로 변형하기 위해 처음 도입됨
단어를 처리해가며 단어 간의 연관성을 파악
구조
- 6개의 동일한 Encoder와 Decoder가 Stack 되어 있는 형태
- Weight를 공유하지는 않는다.
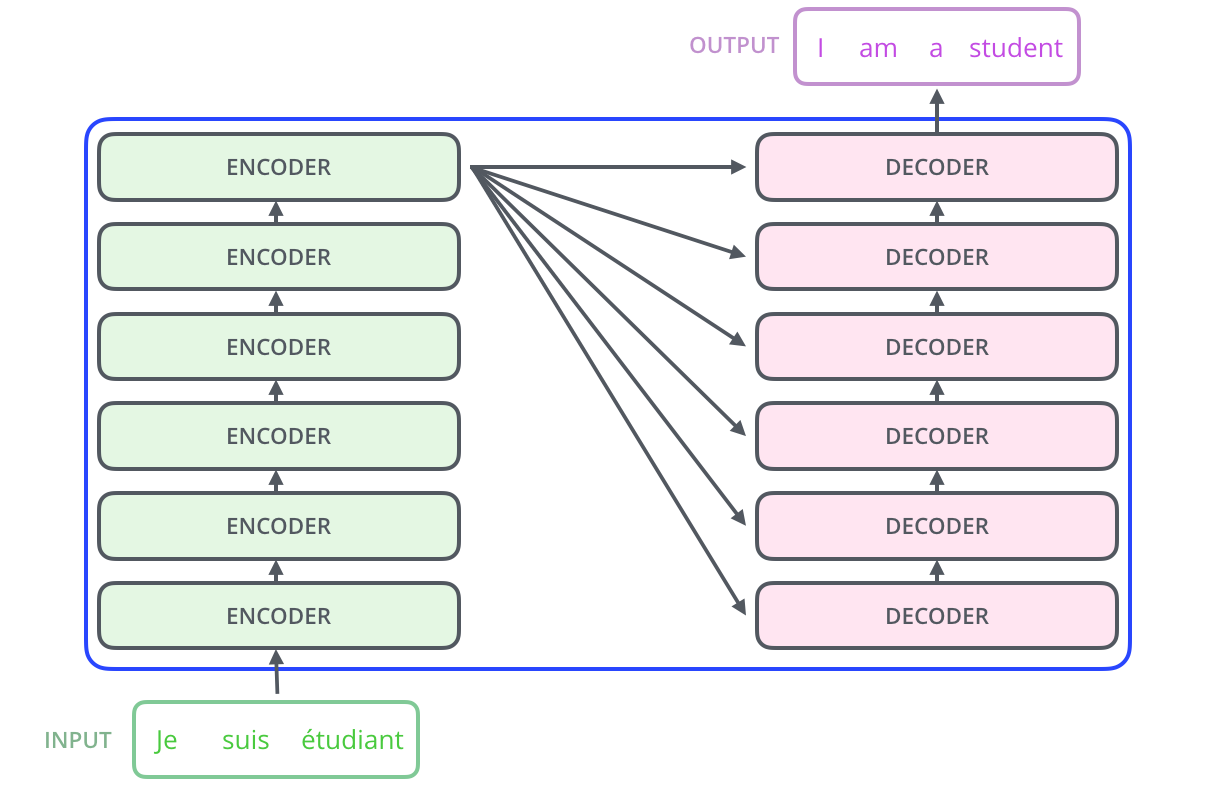
Encoder & Decoder 세부 구조

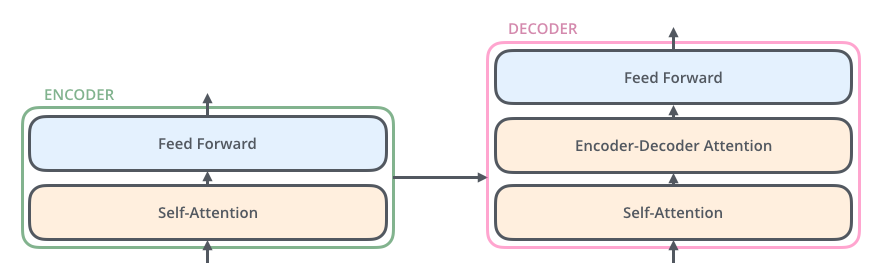
Self-attention

단어 간의 관계성 연산 결과를 활용하여 연관성이 높은 단어끼리 연결해주기 위해 활용하는 것
- 단어에 맥락을 불어 넣어주는 Method
Attention과 비슷하지만, Transformer의 Self-Attention과 Attention 사이에는 몇가지 차이가 존재한다.

Self-Attention VS Attention

Q, K, V 생성
- Attention : Q는 Decoder Cell에서 도출되고, K와 V는 Encoder Cell에서 도출됨
- Self-Attention : Q, K, V는 모두 동일한 Vector(Embedding Vector)에서 도출됨
Time Step
- Attention : Time-Step을 활용함.
- Self-Attention : Time-Step을 활용하지 않음.
- Attention은 이전 Model에서 반환된 Hidden State Vector를 활용한다. 즉, Time Step이 필요한 연산이 된다.
  예를 들어, Time Step이 3이라면 이전 Decoder 2개를 거쳤을 것이고, 이 2개 Decoder의 출력 Data에 대한 정보가 Hidden State Vector에 저장되어 있을 것이다.
- Self-Attention은 이전 단어에 대한 Attention 결과를 활용하지 않는다. 단지, 단어 한 개에 대해 모든 단어에 대하여 Attention Score를 구하므로 이전 연산이 현재 단어에 대한 연산에 영향을 끼치지 못한다. 즉 Time-Step이 의미가 없다.
데이터 보존(Long-term Dependency)
- Attention : Hidden Layer 연산 결과(Hidden State Vector)를 다음 Model에 적용시키는 방식으로 이전 단어 정보를 전달
- Self-Attention : Encoder는 모든 단어에 대하여, Decoder는 이전에 예측했던 모든 단어에 대하여 Q(Hidden Vector)를 구하여, 이 값을 온전히 활용함
- Attention은 시간이 지남에 따라 어쩔 수 없이 초기 해석 정보가 지워지게 된다. 이는 Hidden Layer에 정보가 쌓이다 보면 초기 정보가 사라지는 어쩔 수 없는 현상이다.
  하지만, Self-Attention은 이전 해석 정보에 대한 Hidden State Vector를 보존하여 Self-Attention 연산을 통해 각 단어에 대한 "온전한 Hidden State Vector"와 연산이 수행되게 된다. 즉, Decoder측의 Length가 길어지더라도 초기 Decoder의 해석 정보가 지워지지 않고 온전히 반영될 수 있다는 장점이 있다.
방향성
- Attention은 왼쪽->오른쪽, 혹은 오른쪽->왼쪽의 방향으로 해석이 진행되는 Unidirectional한 Model이다
- Self-Attention은 (Encoder측에서) 오른쪽과 왼쪽에 있는 모든 단어를 활용하는 Bidirectional한 Model이다.
- Attention은 RNN 계열이기 때문에, 이전 단어를 예측하면서 나온 Hidden State Vector를 활용하여 현재 단어를 예측하게 된다. 따라서, 방향성이 존재하게 된다.(이전 단어 예측을 활용하므로, 미래 단어의 예측은 활용할 수 없음) 물론, BiLSTM 같이 왼쪽->오른쪽으로 진행시키고, 오른쪽->왼쪽으로 해석을 동시에 진행시켜 두 결과를 합치는 방법도 존재하지만, Bidirectional 측면에서 바라보면 매우 Shallow 하게 적용되게 된다.
  하지만 Self-Attention의 Encoder에서는 현재 단어의 왼쪽과 오른쪽에 있는 모든 단어에 대하여 연산이 진행되기 때문에, 방향성의 개념이 상당히 적다. 모든 위치에 존재하는 단어와 연산이 진행되기 때문에, Bidirectional Model이라고도 말할 수 있다.
- 즉, Attention은 RNN의 특징으로 방향이 정해졌을 때 자신보다 미래에 Input으로 들어갈 단어들은 활용하지 못하지만, Self-Attention은 (Encoder측에서) 존재하는 모든 단어와 동시에 Attention 연산이 일어나기 때문에 현재 단어가 문장에 어디 존재하는지와는 관계 없이 문장 내 모든 단어를 활용하여 연산이 진행되는 것이다.
- 물론, Decoder 측면에서는 Transformer도 Masking을 활용하므로 방향성의 개념이 존재한다. 나중에 나오겠지만, GPT-n Model은 Transformr의 Decoder를 활용한 Model로써 Unidirectional하지만, BERT는 Encoder를 활용한 Model로써 Bidirectional한 특징을 가지고 있다
Attnention은 RNN을 활용하기 때문에 RNN의 특징을 가지지만 Self-Attention은 오로지 Attention을 활용해서 구현되었기 때문에, RNN이 가지고 있는 특징 및 단점을 가지고 있지 않게 되는 것이다.

Vector를 기준으로 한 Model

입력 Data들을 단어로 나눈 뒤, Embedding Algorithm을 활용하여 Vector로 바꿈
- Input과 직접 연결된 Encoder 측에서만 발생
- 이유 : Vector가 Self-Attention과 Feed-Forward 과정을 거친 이후에도 Vector 형태로 반환되기 때문에, 계속해서 Vector 형태로 전달되기 때문에 1번의 Embedding만 수행하면 됨
$d_k$ : Query Vector와 Key Vector의 Dimension
$d_p$ : Value Vector의 Dimension
- $d_k$ = $d_p$ 일 필요는 없다. 나중에 연산에서 알 수 있지만, 최종적으로 수행되는 연산은 (|Q| X $d_k$ ) * ( $d_k$ X |K|) * (|V| * $d_p$ )이고, |K| = |V|이기 때문에 $d_k$ 와 $d_p$ 는 계산에 영향을 끼치지 않는다
- 물론, Query Vector와 Key Vector의 Dimension은 무조건 동일해야 한다는 사실을 주의하자
- 일반적으로는 $d_k$ = $d_p$ 로 설정하여 Self-Attention 연산을 수행한다.
Self-Attention : 모든 Vector들을 고려하여 변환
Feed-Forward : Self-Attetntion을 통해 바뀐 Feature Vector 각각마다 Independnet하게 Model을 적용하여 반환

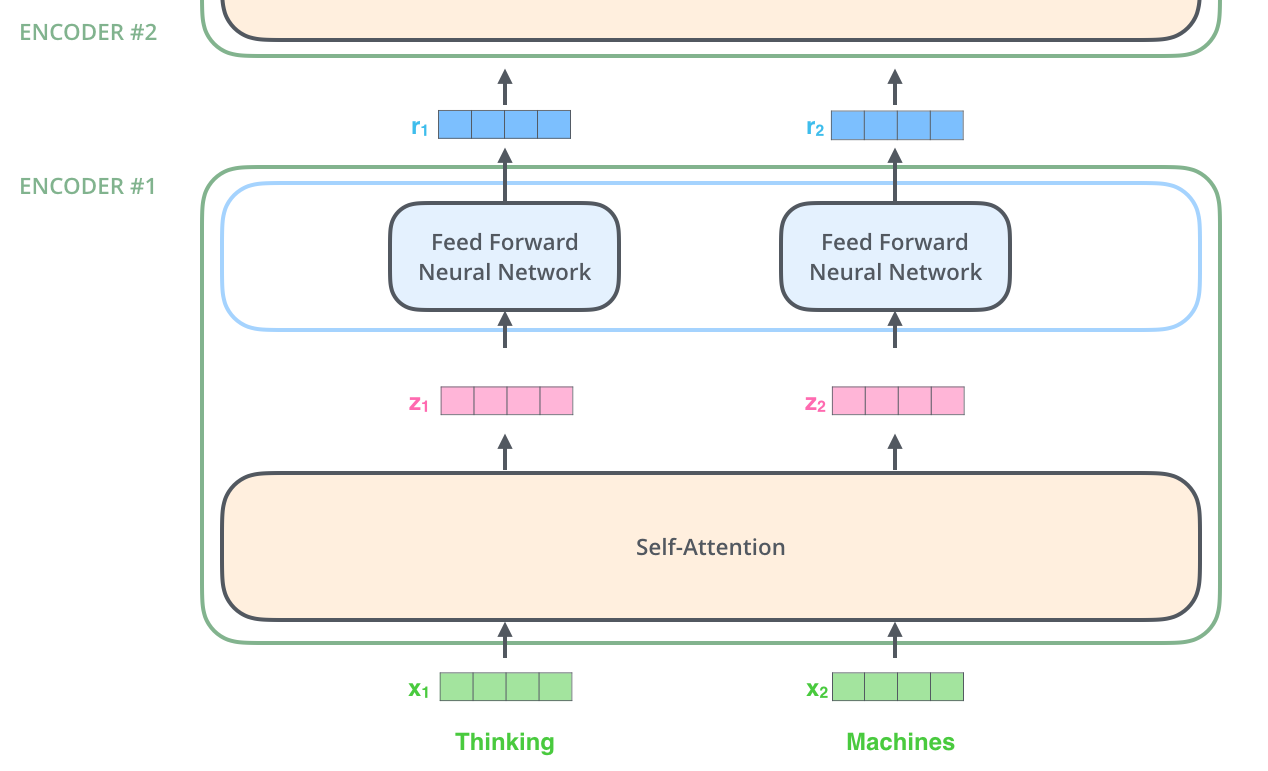
사진으로 보는 Vector Self-Attention(Encoder)

선행 지식
- 입력 Vector들은 크기가 512이지만(Embedding Dimension), Self-Attention 과정에서 활용하는 Vector 크기는 64(Attention Dimension)
- 64로 고정되어 있는 것은 아니지만, Multi-Head Attention의 계산 복잡도를 일정하게 만들고자 내린 구조적인 선택이다.
Self-Attention에서의 Vector 처리 순서

Input 단어들을 활용하여 Embdding Vector 도출
- 단어 1개당 Embedding Vector 1개씩 도출
Embedding Vector를 활용하여 Queries, Keys, Values Vector를 생성
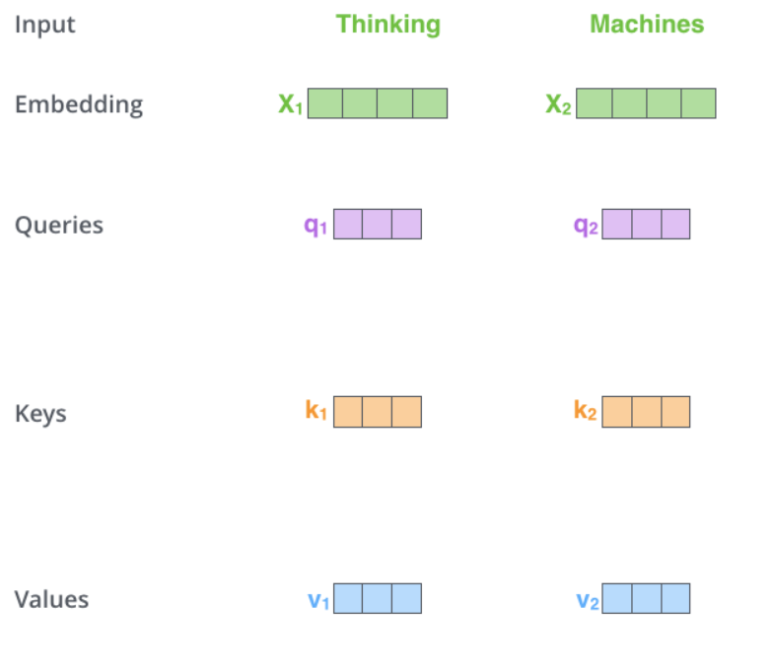
- Embedding Vector 1개당 (Q, K, V) 쌍 1개씩 도출됨
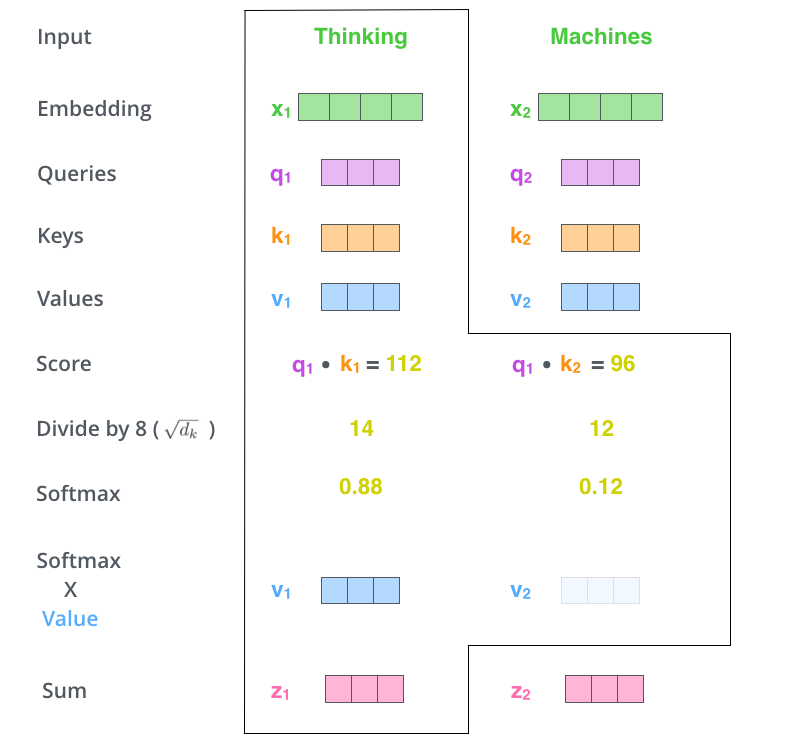
Q, K, V를 활용하여 점수 계산
- 특정 단어의 Query Vector를 활용하여 모든 단어의 Key Vector와 내적을 통해 Score를 구함
- Score : 해당 단어에 대한 Encode를 수행할 때, 다른 단어들에 얼마나 집중해야 할지를 결정해줌
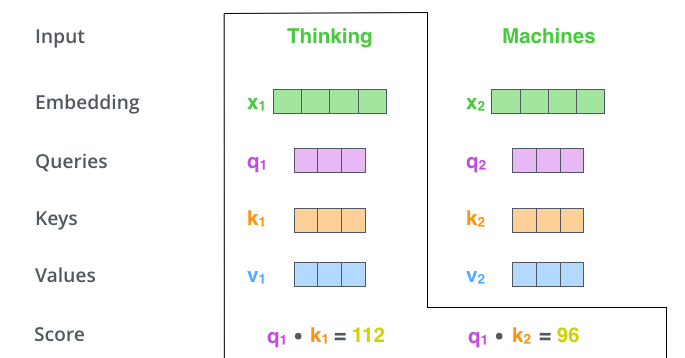
Score를 $\sqrt{d_k}$ 로 나눠줌
- Key Vector Size(Attention Dimension)을 보통 64로 정해주므로, 보통 8로 나눠줌
- $\sqrt{d_k}$ 로 나눠주는 이유
  Query : [a,b], Key : [x, y]라고 했을 때, a, b, x와 y는 평균 0, 분산 1의 확률 변수로 생각해보자. 또한, a, b, x, y는 통계적으로 독립적일 것이다
  그렇다면 $Q*K^T$ 를 수행해주면 ax + by라는 값이 나올 것이다
  ax + by는 평균이 0을 가질 것이고, ax의 분산은 1, by의 분산 또한 1을 가지게 될 것이기 때문에 결과적으로 ax + by의 분산은 1 + 1 = 2가 될 것이다.
  만약 Key Vector의 Dimension( $d_k$ )이 N일 경우, 분산은 위 연산을 활용해본 N이 될 것이고, 표준 편차는 $\sqrt{N}$ 의 값을 가질 것이다.
  문제는 표준편차가 클수록 Softmax의 연산이 큰 값에 몰리는 Pattern이 나타난다. 즉, 표준편차가 작아야 softmax 연산의 결과가 조금 더 고르게 나타난다는 것을 알 수 있다.
  우리는 오로지 내적 값에 의한 Softmax 연산의 불균형을 원하는 것이지, 표준편차나 분산 값에 의해 영향을 받은 Softmax 연산의 불균형을 원하지는 않는다.(실제로는 비슷한 확률을 가지는데 표준편차 때문에 값이 몰린다면 학습이 안정화되지 않는다)
  따라서, 위 연산에서 나오듯 표준 편차는 $\sqrt{d_k}$ 값을 가질 것이기 때문에 이 수로 나눠주어 표준편차를 1로 만들어준다.
  최대한 $Q*K^T$ 연산 결과 이외에는 Softmax 연산에 영향을 주지 않아 학습을 안정화시키기 위해서 $\sqrt{d_k}$ 로 나눠주는 과정이 추가되야 하는 것이다.
나눠준 모든 값을 Softmax 함수에 통과시켜줌
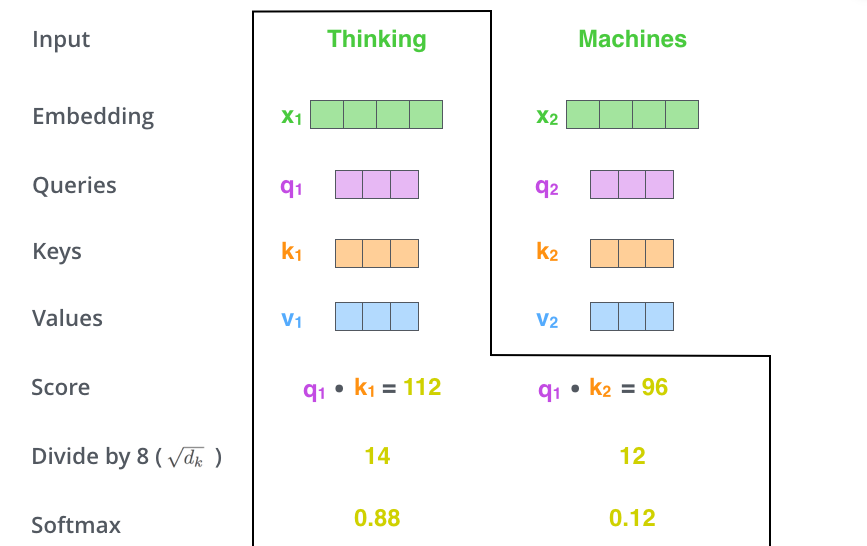
Softmax 연산 결과값들을 Value 벡터에 곱해줌
- 관련 있는 단어들은 남겨주고, 관련이 거의 없는 단어들은 없애버리기 위한 과정
- softmax 연산의 결과값을 가중치로 활용하여 단어들의 비중을 결정하는 과정
Value 벡터를 곱해준 모든 Vector들을 더해줘 나오는 Vector가 해당 단어가 Self-Attention을 거친 이후 반환할 Self-Attention Layer의 출력값이 됨

사진으로 보는 Matrix Self-Attention(Encoder)

단어를 한개의 Matrix로 합쳐 한꺼번에 계산을 수행할 수 있음
Embedding Vector를 x축 방향으로 쌓아 행렬을 생성
- 아래 단어에서는 X축은 2개의 Row를 가지는데, 이는 총 2개의 단어에 대한 연산을 한번에 수행하는 것이다.
연산 순서

Embedding Vector를 하나의 행렬 X로 만들어줌
X에 우리가 학습할 가중치 행렬인 $W^Q, W^K, W^V$ 를 곱하여 Q, K, V를 구함
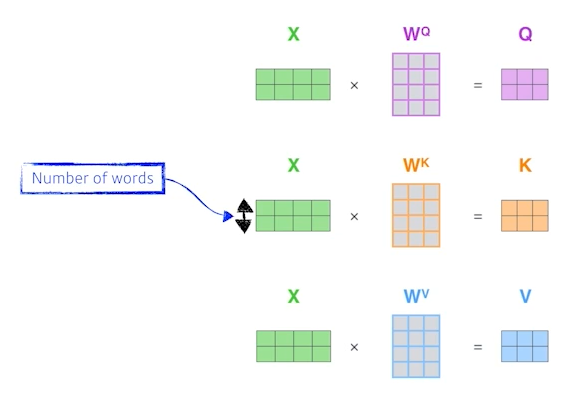
행렬 연산을 통해 Self-Attention 과정을 한꺼번에 수행할 수 있음
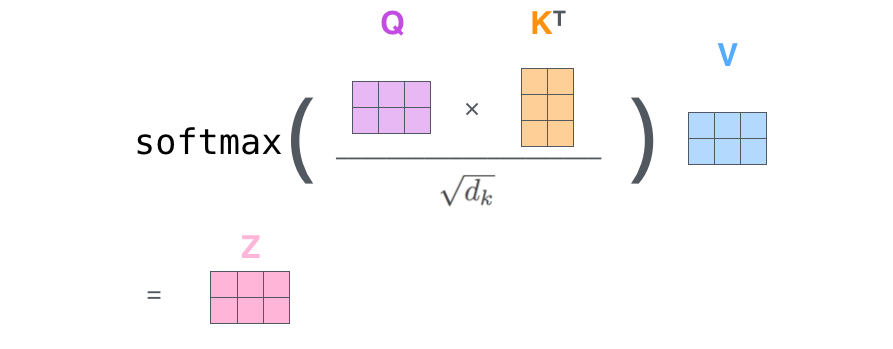
- Softmax 연산 : Row-wise Softmax
  - 즉, Row별로 Softmax를 수행하는 것

Multi-Headed Attention

2가지 방법으로 Attention Layer 성능을 향상시킴
- Model이 다른 위치에 집중하는 능력을 확장시킴
  - 자신에 대한 Score가 너무 높아 다른 단어와의 연동이 필수적인 상황에서 제대로 연결되지 못하는 상황을 해결
- Attention Layer가 여러 개의 Representation 공간을 가지게 해 줌
  - 여러 개의 (Q, K, V) Weight 행렬들을 가지기 때문에, 학습 후에 각 Vector들을 목적에 따라 여러 개의 Representation 공간으로 나타낼 수 있음
여러 개의 Attention Head를 가지며, Attention Head는 (Q, K, V) 연산을 위한 각각의 W(가중치 행렬)을 가짐
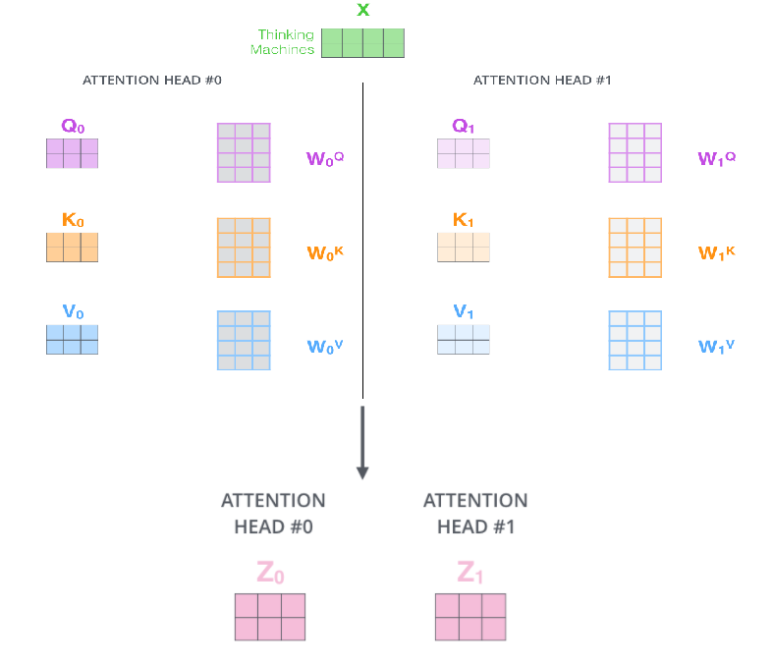
- Attention Head마다 서로 다른 Z(Self-Attention 결과값)을 반환함
사진 설명
- Attention Head를 2개 생성하여 X를 각각의 Attention Head에 적용시켜줌
- 직관적인 관찰을 위해 Attention Head를 2개만 생성한 Case를 보았지만, 보통 Attention Head를 매우 많이 생성한다.
Multi-Headed Attention 반환 행렬 처리
```
<설명>
위 사진처럼 도출된 수많은 Attention Head를 바로 
Feed-Forward Layer로 보낼 수는 없다.
Feed-Forward는 1개 행렬이나 벡터에 대해서만 Input으로 받을 수 있다.
즉, 여러 개의 Attention Head에 의해 도출된 결과값들을 어떤 방식으로든 합쳐 
행렬의 Size를 1개의 Head가 반환하는 행렬의 Size와 동일하도록 
맞춰 줄 필요가 있는 것이다.
```
- 방법
  - 아래 설명한 방식과 나중에 Code를 통해 구현한 방식은 차이가 존재함
1. 여러 개의 행렬을 모두 이어 붙여 하나의 행렬로 만듦
  - 만약 Attention Head가 8개이고 Attention Dimension이 10이라면, 결과 행렬을 모두 이어 (n X 80) 형태를 가지는 행렬꼴로 만드는 것이다.
2. 위에서 구한 Weight 행렬에 새로운 가중치 행렬 $W_0$ 를 곱하여 Attention Dimension을 맞춰줌
  - 위 예시에서 (n X 80) 형태를 만들었으므로, (80 X 10) 형태의 $W_0$ 행렬을 만들어 곱해줌
  - $W_0$ 또한 학습을 통해 Update 시켜야 함
- 나중에 구현할 코드와의 차이점

원래 만들어지는 Q, K, V가 100 Dimension Feature를 가진다고 가정하자.
위 방식은 100 Dimension을 가지는 서로 다른 (Q, K, V)를 여러개 만드는 것이다.

코드로 구현한 방식은 먼저 100 Dimension을 가지는 Q, K, V를 생성한다.(1개만!)
이렇게 만들어진 Q, K, V를 head 개수만큼 쪼개는 것이다.
(예를 들어 Head가 5개라면, 20 Dimension을 가지는 5개 Q, K, V로 쪼개는 것이다)
이후 softmax(QKᵀ)V 연산을 각각 쪼갠 Q, K, V에 대해 모두 수행해주고,
수행된 결과를 마지막에 Concat시켜 MHH를 구현한 것이다.
(위 예시로 보자면, 5개의 서로 다른 20 Dimension Q, K, V에 대해 각각 
Attention Function을 수행해주고, 이 과정으로 만들어진 20 Dimension 행렬 5개를 
Concat 시켜 최종적으로 100 Dimension Feature 꼴을 맞춰주는 것이다)

Multi-Headed Attention의 활용 방법
- Attention Head 1개마다 연관성이 큰 단어들을 찾을텐데, 이 때 Head마다 관찰할 관계성을 다르게 하여 연산을 수행하는 것이다. 따라서 Representation 공간이 넓어진다.
- 그림을 통한 예시
- 위 그림을 보면 주황색 Attention Head는 Animal과 가장 큰 연관성을 가지고, 초록색 Attention Head는 Tired와 가장 큰 연관성을 가진다. 즉, it은 이 2개 단어에 대해 연고나성을 맺고 있다.
- 여기서 Representation 공간이 넓어진다는 의미가 무엇인지 알 수 있다. 예를 들어 Attention Head가 하나였다면 Tired나 Animal 둘 중 하나에만 더 집중해서 봤을 것이고, 따라서 아무래도 2개 중 한 개의 단어에 대해서는 덜 집중해서 분석할 것이다. 하지만, 이 2개 단어 모두 it에게는 중요한 단어이다. 단, 중요성의 방향이 다를 뿐이다.
- 주황색 Attention Head는 "그것이 무엇인가"에 집중하여 관찰한 것이고, 초록색 Attention Head는 "그것이 어떤 상태인가?"에 집중하여 관찰한 것이다. 즉, 서로 다른 방향성을 가지고 단어 간의 관계성을 파악하고, 이를 통해 중요한 2개 단어를 모두 활용할 수 있게 되는 것이다.

Time Complexity

n : Sequence Length
d : dimension of representation
k : Kernel Size
r : size of the neighborhood in restricted Self-attention
- restricted Self-attention : 문장 길이가 너무 길 경우 일정 길이(r)로 문장을 쪼개 Self-attention을 수행하는 것
Complexity per Layer : 작을수록 시간이 적게 걸림
Sequential Operations : 병렬화할 수 있는 계산의 양
Maximum Path Length : 장거리 의존성
Self-attention 설명
- Compleixty per Layer
  $QK^T$ 연산은 Sequence Length만큼 수행되기 때문에, 총 $n^2$ 만큼의 연산이 수행된다.
  이후 Dimension만큼 "+"연산이 수행되므로, 총 Time Complexity는 $O(n^2d)$ 가 된다.
- Self-attention의 Memory : 모든 단어 사이의 내적값을 저장해야하므로 메모리가 많이 필요함
- Sequential Operation
  메모리가 매우 많다고 가정했을 때, Self-attention의 $QK^T$ 연산은 다른 연산에 의해 영향을 받거나 영향을 주지 않으므로, O(1)의 Sequential Operations를 가짐
- Maximum Path Length
  Layer 1개에서 현재 확인할 수 있는 단어에 대해 검색할 수 있다.(Self-attention에 모든 Q, K, V가 저장되어 있으므로) 따라서, O(1)의 값을 가진다.
RNN 설명
- Compmlexity per layer
  Hidden State Vector의 Dimension이 D이다. 가중치 행렬 W는 $d \times d$ 형태롤 가지므로 1개 Sequence에 대하여 $O(d^2)$ 의 Compleixty를 가진다. 총 N개의 Sequence가 존재하므로, $O(nd^2)$ 의 Time Compleixty를 가진다.
- Sequential Operations
  $h_{t-1}$ 을 구해야만 $h_t$ 를 구할 수 있다. 즉, 메모리가 많아도 이전 Hidden State Vector 연산 결과를 기다려야 하므로 Sequential Operation이 O(n)의 값을 가진다.(병렬화가 힘들다)
- Maximum Per Length
  Layer를 N개 거쳐야지만 현재 Model에서 다음 단어를 예측할 수 있으므로, O(n)의 값을 가진다.

Positional Encoding

단어들의 위치 정보를 고려해주기 위해서 Transformer에서 적용한 기법
- Seq2Seq는 두 단어 사이 거리가 멀면 Hidden State Vector에서 값이 점점 없어지기 때문에, 위치적 정보가 자연적으로 적용된다. 하지만, Transformer는 모든 단어와 연산이 진행되므로, 해당 단어와 특정 단어 사이 거리가 매우 멀더라도 이런 정보를 알려줄 방법이 없다
- 따라서, 두 단어 사이의 거리에 대한 정보를 간접적으로 알려줄 방법이 필요하고, 이것이 Positional Encoding이다.
- 물론, 두 단어 사이 거리가 멀더라도 연산이 온전하게 적용된다는 것이 Transformer의 장점이지만, 그래도 단어의 위치 정보 자체는 중요하다라는 생각에 나온 기법이다
  - 어순은 언어를 이해하는 데 중요한 역할을 하므로, 이런 정보에 대한 처리가 필요함
Positional Encoding : 단어들의 위치 정보를 고려하기 위해 활용하는 Vector
- Embedding Dimension과 같은 크기를 가짐
- (Q, K, V) 벡터들로 인한 연산으로 단어들 간의 거리를 늘릴 수 있다는 점을 활용한 방법
Embedding Vector에 Positional Vector를 "더해주어" Embedding with time Signal Vector를 형성하고, 그렇게 형성한 Vector를 첫번째 Encoder에 넣어주는 방식
cos, sin 함수를 활용하여 토큰의 위치정보 보완
cos, sin 함수를 활용하는 이유
- cos, sin 대신 정수값으로 Positional Encoding을 수행하면 Positional Encoding 값이 모델에 끼치는 영향이 지나치게 커질 수 있으며, 이는 robustness 측면에서 좋지 않다.
- 아래 4가지 조건을 충족시키기 때문에 cos, sin을 활용함
1. 각각의 고유한 토큰 위치 값은 유일한 값을 가져야함
2. 서로 다른 두 토큰이 떨어져 있는 거리는 일정해야 함(1-2 토큰과 2-3 토큰의 거리 차이는 같아야 함)
3. 긴 길이의 문장들도 무난히 표현해야 함
4. 함수에 따른 토큰 위치 값이 예측 가능해야 함
수식
$PE_{(pos, 2i)} = sin(pos/1000^{2i/d_{model}})\newline PE_{(pos, 2i+1)} = cos(pos/1000^{2i/d_{model}})$
- d : 전체 Dimenion 수
- pos : 각각의 토큰의 위치정보값
  - 정수 값을 가짐
- 한 Vector의 짝수 Dimension에는 sin 값을, 홀수 Dimension에는 cos값을 적용함
짝수, 홀수 위치에 각각 sin, cos을 적용시켜주는 이유
- 홀수, 짝수 위치에 관계없이 cos, sin 중 하나만을 적용한다면, 특정 두 토큰의 위치 값이 동일해질 수 있음
  - 주기 함수의 특징
- 이 경우, 각각의 고유한 토큰 위치 값은 유일한 값을 가져야한다는 조건을 충족시킬 수 없으므로, cos과 sin을 동시에 활용하여 이런 문제를 해결함

Residual Connection

Self-attention의 Add 과정
CV에서 깊은 Layer Neural Net을 만들 때 Gradient Vanishing 문제를 해결하고자 활용한 효과적인 Modeling 방법
입력 Vector가 존재할 때, Multi-Head Attention을 거친 Output Vector에 입력 Vector를 더해주는 방법
- 입력 Vector가 x이고, Self-attention을 거친 Vector가 f(x)일 경우, f(x) + x연산을 통해 입력 Vector도 활용해주는 것
- Resnet의 Skip-Connection
- Model의 Output Vector와 입력 Vector의 Dimension은 동일해야 함
학습을 안정화시킬 수 있음

Layer Normalization

Batch Normalization을 수행한 뒤 Affine Transformation을 수행하는 과정
- Batch Normalization : https://velog.io/@idj7183/Regularization
Affine Transformation
- 최적화 가능한 Parameter를 활용하여 수행해주는 과정
- 내가 원하는 평균과 표준편차를 Normalization한 값에 주입하는 수식
  - 평균이 0, 표준편차가 1인 Data Set을 y = 2x + 3이라는 함수에 넣어 값을 변형시킨다. 그렇다면 2 * 0 + 3 = 3이 평균, |2|*1 = 2가 표준편차가 될 것이다. 이 때, 2와 3은 학습 가능한 Parameter이다.
- Layer의 Node별로 수행함. 즉, Batch Norm과는 다른 방향으로 수행됨
예시

thinking : (4,2,3,5), machines : (2,1,-3,2)의 Vector로 표현된다고 가정하자

thinking의 평균은 3.5, 1.11이고 machines의 평균은 0.5, 표준편차는 2.06이다.
이를 활용하여 Batch Normalization을 수행하면, 
thinking : (0.65, -0.45, -1.35, 1.25), 
machines : (0.7, -1.5, -0.3, 1.1)의 Vector로 변환되게 된다.

이후 Affine Transformation을 수행해준다.
Layer의 Node별로 수행해줘야 하기 때문에, 총 4개의 함수가 필요할 것이다
(단어 Vector의 Dimension마다 적용시킬 함수가 존재해야 함)

Dimension = 1에는 y = 3x + 1, 2일 떄는 y = x+1, 
3일 때는 y = -x, 4일 때는 y = -2x+2를 적용시킨다고 가정하자.

그렇다면, Layer Normalization을 거친 최종 Vector 값은
Thinking : (2.95, 0.55, 1.35, -0.5), Machines : (3.1, -0.5, 0.3, -0.2)가 
될 것이다.

Warm-up Learning Rate Scheduler

초기 lr(initial Learning Rate)를 먼저 설정한다. 시작시 매우 작은 lr(learning rate)로 출발하여 lr을 선형적으로 증가시켜 초기 lr 값에 도달하게 한 다음, 초기 lr에 도달하면 다시 lr을 (내가 원하는 방식으로) 감소시키는 기법
Transformer가 활용한 leraning rate 기법
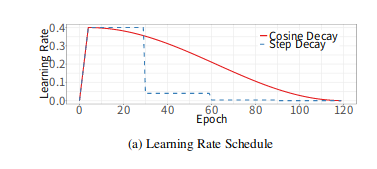
활용 이유
- Training이 시작될 때 Parameter는 최종 Solution에서 멀리떨어져 있음
- 너무 큰 lr을 활용하면, Numerical Instability가 발생할 수 있음
- 이를 위해 초기에는 작은 lr을 사용하고, Train 과정이 안정되면 초기 Learning Rate로 전환하는 방법인 Warm-up learning Rate를 활용

Self-attention Encoder 및 Decoder Layer

Encoder
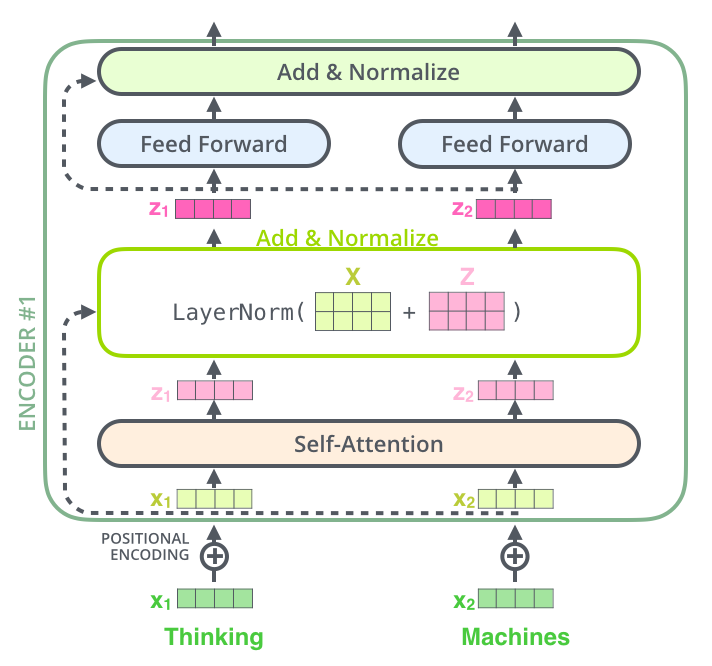
왼쪽 : Encoder, 오른쪽 : Decoder

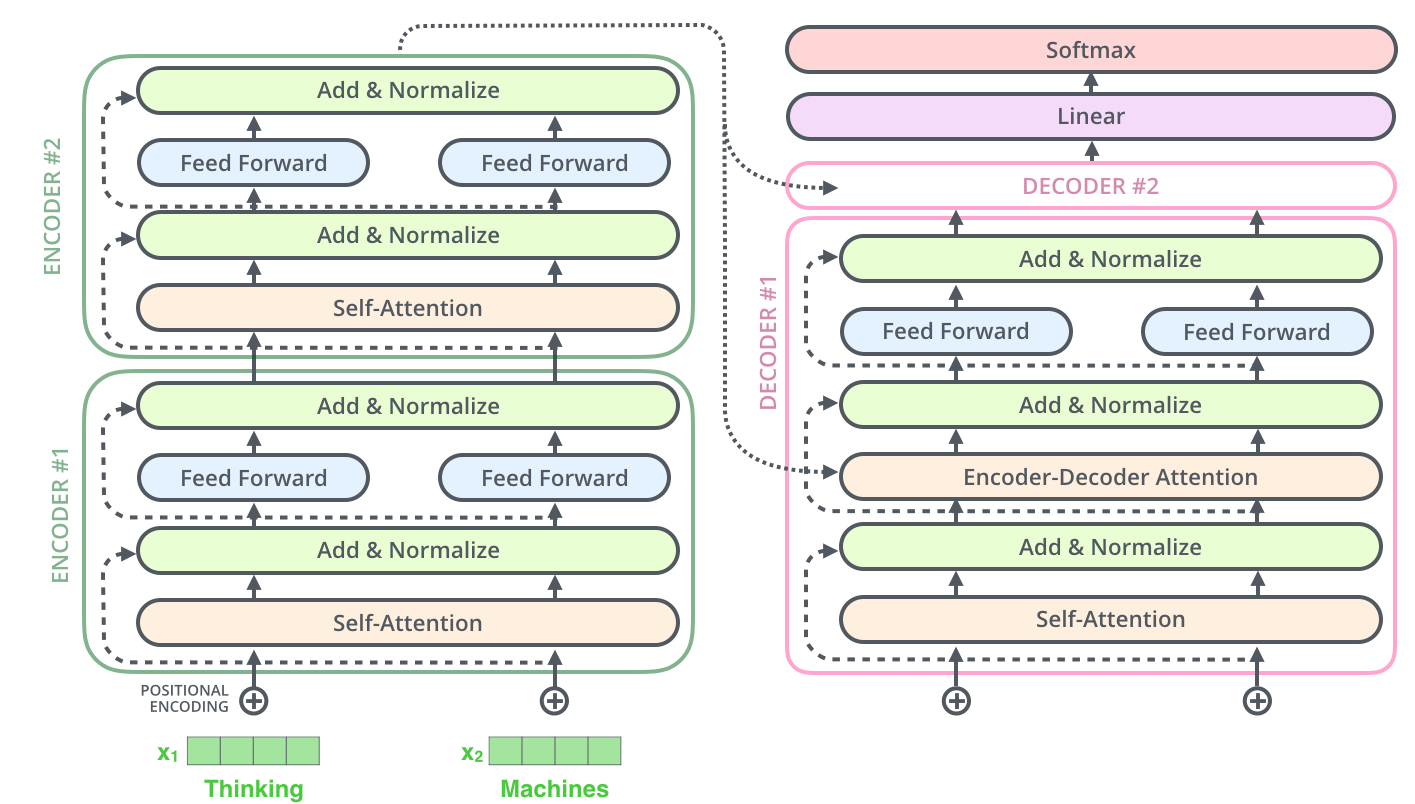
Decoder 과정

Encoder와는 달리, K와 V는 Encoder 측에서 받아 활용
- Encoder는 Input 단어들에 대하여 Q, K, V를 모두 생성했지만, Decoder는 K, V는 Encoder측에서 받아오고 Q만 해당 단어에 대해서 만들어 활용
Decoding의 Self-Attention Layer에서는 Masking을 수행함
- Masking : Decode를 수행할 현재 위치 데이터에 대하여 이전 위치들의 Data(즉, Decode가 완료된 Data)들에 대해서만 접근 및 활용할 수 있도록 해주는 방법
- 미래 정보를 고려하지 않고 이전에 Decode를 완료한 단어에 대해서만 Dependent하도록 만듦
- Masking 방법 : 미래 데이터에 대해 $-\inf$ 값으로 치환하여 해당 Data를 고려하지 않도록 함

Teacher Forcing

Decoder의 처음 성능이 좋지 않기 때문에 학습이 방해가 되는 것을 줄이기 위한 기법
Seq2Seq(Encoder-Decoder) 기반으로 한 Model에서 자주 활용되는 기법
실제 Target을 Decoder의 다음 입력으로 넣어주는 기법

<설명>
Decoder의 처음 성능은 당연히 매우 좋지 않을 것이다.
Sequential Data는 설명했듯이 이전까지의 데이터가 현재 데이터에 영향을 미치는
데이터인 Case가 매우 많다.
처음 Decoder는 성능이 좋지 않기 때문에 당연히 처음에는 단어 예측을 실패할 것이고,
이렇게 실패한 단어 예측은 나비효과를 일으켜 다음 학습도 실패하도록 유도하게 된다

따라서 이런 문제를 해결하기 위해 나온 기법이 Teacher Forcing이다.

Teacher Forcing이 진행되지 않은 상황에서는 다음 Decoder의 입력값으로
이전 Decoder에서 해석한 단어에 대한 정보가 들어갈 것이다.
하지만, 이전 Decoder가 잘못 해석하였다면 당연히 현재 Decoder의 예측도 실패할
가능성이 높아질 것이며, 이는 성능 하락과 학습 시간 증가의 요인이 될 것이다.
따라서, 처음 Decoder의 성능이 나쁠 때는 실제 Target값(Label 값)을 Decoder의
Input으로 넣어주고, Decoder의 성능이 어느정도 좋아졌을 때부터 원래대로
이전 Decoder의 Output을 다음 Decoder의 Input으로 넣어주는 것이다.

Teacher Forcing에서 넣어주는 Target Data를 Ground Truth라고 하는데,
이 Ground Truth를 활용하여 초기 Decoder의 성능을 올려 초기 학습 정확도를
올리는 기법을 Teacher Forcing이라고 한다.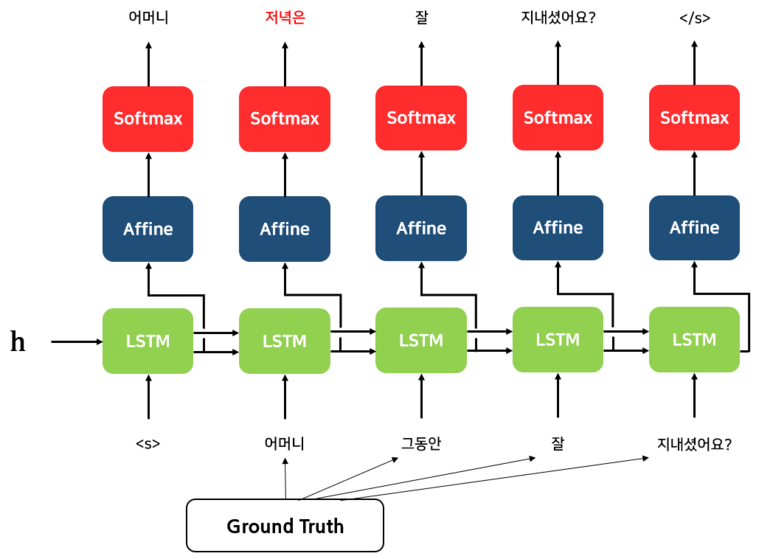

장점 : 빠른 학습
- 초기 정확도가 낮은 Decoder 때문에 많은 오류가 생겨 학습에 시간이 더 소요되는 것을 막아줌
노출 편향 문제(Exposure Bias Problem)
- 추론 과정에서는 Ground Truth를 넣어줄 수 없으므로 학습 단계와 추론 단계 과정에서 차이가 생겨 모델 성능과 안정성에 영향을 미침
- 큰 영향을 끼치지는 않는다는 연구가 존재(T. He, J. Zhang, Z. Zhou, and J. Glass. Quantifying Exposure Bias for Neural Language Generation (2019), arXiv.)
공부 사이트 : https://blog.naver.com/PostView.naver?blogId=sooftware&logNo=221790750668

사진 출처
https://wikidocs.net/22893
https://nlpinkorean.github.io/illustrated-transformer/
https://blog.naver.com/PostView.naver?blogId=sooftware&logNo=221790750668
https://jeddy92.github.io/JEddy92.github.io/ts_seq2seq_intro/
https://www.researchgate.net/figure/Compare-the-computational-complexity-for-self-attention-where-n-is-the-length-of-input_tbl7_347999026
https://blog.airlab.re.kr/2019/07/bag-of-trick

DONGJIN IM

개념부터 확실히!

이전 포스트

Decoding, BLEU

다음 포스트

Attention, Transformer(Self-Attention)

AI(NLP) 이론

Attention

Seq2Seq

Attention이란?

Attention 특징

Attention Mechanism

Dot-Product Attention

Attention 수행 순서

Transformer

Transformer란?

Self-attention

Self-Attention VS Attention

Vector를 기준으로 한 Model

사진으로 보는 Vector Self-Attention(Encoder)

사진으로 보는 Matrix Self-Attention(Encoder)

Multi-Headed Attention

Time Complexity

Positional Encoding

Residual Connection

Layer Normalization

Warm-up Learning Rate Scheduler

Self-attention Encoder 및 Decoder Layer

Decoder 과정

Teacher Forcing

Decoding, BLEU

Self-Supervised Pre-trainig Model

0개의 댓글