확률변수

확률 변수의 종류

	이산확률변수	연속확률변수
정의	확률변수 X가 취할 수 있는 값이 유한하므로 셀 수 있는 확률변수	확률변수 X가 취할 수 있는 값이 어떤 범위에 속하는 모든 실수로 무한하기 때문에 셀 수 없는 확률 변수
고려할 점	확률 변수에 있어서 경우의 수	확률변수 밀도 그래프
수식	$P(X\in A) = \sum_{x\in A} P(X=x)$	$P(X\in A) = \int_{x\in A} P(X=x)$

분류 문제에서는 softmax 함수를 활용하여 조건부 확률 계산하며, 회귀 문제에서는 조건부 기댓값을 추정하여 L2 norm을 최소화 시키는 방향으로 계산을 수행한다.

기대값

데이터를 대표하는 통계량으로, 확률을 분포를 통해 다른 통계적 범함수를 계산하는데 활용한다.
(분산, 첨도, 공분산 등 여러 통계량 계산에 사용됨)

• 연속 확률 변수에서의 기댓값 계산
  $E_{x\sim P(x)}[f(x)] = \int_{X} f(x)P(x)dx$
• 이산 확률 변수에서의 기댓값 계산
  $E_{x \sim P(x)}[f(x)] = \sum_{x\in X} f(x)P(x)$

몬테카를로 샘플링

확률분포 P(x)를 모를 때 활용하는 방법으로, 변수 유형(이산, 연속)에 상관 없이 활용할 수 있는 방법이다.

대수의 법칙(law of large number)에 의해 수렴성을 보장하는데, 대수의 법칙이란 데이터 수가 많으면 모집단에서 무작위로 뽑은 표본의 평균이 전체 모집단의 평균과 가까울 가능성이 높다는 통계와 확률 분야의 기본 개념이다.
(모집단 : 모든 데이터)

• 필요한 조건
  1. 확률 변수 $X_1, X_2, ..., X_n$이 상호 독립적. 즉 독립 추출이 보장됨
  2. 모든 확률변수가 동일한 확률분포를 가짐
• 아래 수식에 Sample Data$(x^{(i)})$를 충분히 많이 입력시키면 P(x)를 몰라도 유사한 기댓값을 구할 수 있음
  $E_{x\sim P(x)}[f(x)] \approx \frac{1}{N}\sum_{i=1}^N f(x^{(i)})$

---

표본집단

표본 집단이란?

• 모집단 : 연구자가 알고 싶어하는 대상 또는 효과의 전체 집단
  모수 : 모집단을 조사하여 얻을 수 있는 통계적인 특성치
• 표본집단 : 모집단의 부분집합

통계적 모델링

적절한 가정 위에서 확률분포를 추정하는 것을 목표로 하며, 기계학습과 통계학이 공통적으로 추구하는 목표이다.

모수적 방법론이란 데이터가 특정 확률 분포를 따른다고 가정한 뒤 분포를 결정하여 모수를 추정하는 방법이다.
반대로 비모수적 방법론은 특정 확률 분포를 먼저 가정하지 않고 데이터에 따라 모델의 구조 및 모수 개수를 유연하게 바꾸는 방법이다.

정규 분포의 모수를 추정할 때, "표본평균"과 "표본 분산"을 통해 추정허는데, 분산을 구하는 계산식에서 모분산을 구할 때 N으로 나누는 것과는 다르게 표본분산은 (N-1)로 나눈다는 특징을 가지고 있다.

중심 극한 정리(Central Limit Theorem)

표본 평균의 표집분포 N이 커질 수록, 정규 분포 $N(\mu,\sigma ^2/N)$을 따른다는 정리이다.

표집분포(Sampling DistributioN)란 통계량의 확률 분포를 말하며, 모집단의 분포가 정규 분포를 따르지 않아도 성립하는 정리이다.

최대 가능도 추정법(Maximum Likelihood Estimation, MLE)

주어진 표본에 대해 가능도(확률)를 가장 크게 하는 모수 $\theta$를 찾는 방법이다.

어떤 모수가 주어졌을 때, 원하는 값들이 나올 가능도 함수를 최대로 만드는 모수를 선택하는 방법이다.

확률 변수 $X_1, X_2..., X_n$의 확률 밀도 함수를 $f(x|\theta)$라고 하자. x = $(X_1, X_2..., X_n)$일 때 가능도 함수는 아래 수식과 같다

• $L(\theta | x) = f(x|\theta)$

가능도 함수의 정의는 모수가 $\theta$일 때 주어진 표본 x가 얻어질 확률을 구하는 것으로, 여기서 중요한 점은 가능도 함수는 x에 의한 함수가 아닌, $\theta$에 대한 함수라는 점이다.
x는 이미 정해진 확률 변수 값으로써 들어갔기 때문에, 즉, 상수 처리 되기 때문에 바뀔 수 있는 값은 오직 $\theta$밖에 존재하지 않기 때문이다.

• $L(\theta | x) = f(x|\theta)$
  $= f(X_1, X_2, ..., X_n | \theta) = f(X_1 | \theta) * f(X_2 | \theta) * ... * f(X_n | \theta)$
  $= \prod_{i=1}^n f(X_i | \theta)$

가능도 함수가 크다는 의미는 만약 모수가 내가 임의로 정한 $\theta$일 때 표본인 x가 수집될 확률이 높다는 의미로 주어진 표본 x의 모집단일 확률이 커진다는 의미이기 때문에, 자연스럽게 표본들을 뽑은 모집단과 일치할 가능성이 높아진다는 의미이며, 자연스럽게 모수도 같아질 확률이 높아진다는 것이다.
즉, 최대 가능도 추정법은 이러한 이유로 가능도 함수를 최대로 만드는 모수 $\hat{\theta}$를 찾는 것이다

MLE 수식

• 일반 : $\hat{\theta} = argmax(L(\theta | x))$
• 로그 가능도를 활용한 MLE 수식
  $log(L(\theta | x)) = log(f(x | \theta)) = \sum_{i=1}^n log(P(x_i | \theta))$
  • 마지막으로 나온 Sum값을 가장 크게 하는 $\theta$를 찾으면 됨

MLE 수식에 로그 가능도를 활용하지 않으면 "곱 연산"이 수행되게 되는데, 이 경우 2가지 문제가 발생한다.
1. UnderFlow나 Overflow의 위험도가 매우 커진다.
2. 너무 많은 데이터를 계산할 경우 컴퓨터가 가진 한계로 정확한 계산이 불가해지거나 계산이 아예 불가능해질 수도 있다.

이러한 문제를 해결하기 위하여 로그 가능도를 활용한다.

---

확률 분포 사이의 거리

확률 분포 사이의 거리를 유도하는 방법

손실 함수(Loss Function)은 모델이 학습한 확률 분포와 데이터의 확률 분포를 비교하여 유도한다.
그렇다면, 이 두 개의 확률 분포를 어떻게 활용할까?

여기서 DL에서는 확률 분포의 거리를 활용한다.
즉, 모델이 학습한 확률 분포와 데이터의 확률 분포를 구하고, 그 2개의 거리가 가장 짧게 만드는 방향으로 학습을 진행하는 것이다

대표적인 확률 분포 사이 거리를 구하는 방법은 아래와 같다.

• 총변동 거리(Total Variation Distance, TV)
• 쿨백-라이블리 발산(Kullback-Leibler Divergence, KL)
• 바슈타인 거리(Wasserstein Distance)

쿨백-라이블러 발산

최대 가능도 추정법은 곧 쿨백-라이블러 발산을 최소화하는 것과 똑같은 의미를 가진다.

• 쿨백 라이블러 발산(KL Divergence) 정의
  • 연속 확률 변수 : $KL(P||Q) = \int_{X} P(x)log(\frac{P(x)}{Q(x)})dx$
  • 이산 확률 변수 : $KL(P||Q) = \sum_{x\in X}P(x)log(\frac{P(x)}{Q(x)})$
• KL Divergence 분해
  $KL(P||Q) = -E_{x\sim P(x)}[log(Q(x))]_ + E_{x\sim P(x)}[log(P(x))]$

                                 (크로스 엔트로피)             (엔트로피)

  • 정답 Label : P, 모델이 예측한 Label : Q

Classification문제를 해결할 때,
최대가능도 추정법에서 활용되는 Loss Function = (크로스 엔트로피)
의 관계를 가지게 된다.

결국 모델은 Loss Function을 최소화 시킨는 것이 목표이고, 이는 크로스 엔트로피를 최소화 시킨다는 의미이며, 이는 쿨백-라이블러 발산을 최소화 시키는 것으로 이어진다.

---

Bayes Theorem

조건부 확률

• 정의 : 사건 B가 일어난 상황에서 A가 발생할 확률
• 표현식 : $P(A|B)$
• 수식 : $P(A|B)P(B) = P(A\cap B)$

Bayes Theroem

• 목표 : 사후확률을 구하는 것
  $P(\theta | D) = P(\theta) * \frac{P(D | \theta)}{P(D)}$
  • 사후확률(posterior) : 구하고 싶은 확률 $\Rrightarrow P(\theta | D)$
  • 사전확률(prior) : 사건이 일어날 확률 $\Rrightarrow P(\theta)$
  • 가능도(likelihood) : 사건이 일어났을 때 사전 조건이 발생했을 확률 $\Rrightarrow P(D | \theta)$
  • 증거(evidence) : 사전조건이 일어날 확률 $\Rrightarrow P(D)$
  • 주로 D는 눈으로 볼 수 있는 결과(관찰 가능한 결과), $\theta$는 눈으로 관찰 불가능한 사건으로 설정하는 경우가 많음
    • (ex) 코로나가 걸렸는지 여부 : $\theta$, 코로나 검진 결과 : D
• Bayes Theroem을 활용하여 사전확률을 갱신하고, 이를 통해 정확도를 높일 수 있음
  1. $P(\theta | D)$를 구함(사후 확률)
  2. 1번에서 구한 사후 확률 값으로 사전 확률 갱신(사전 확률 = 이전에서 구한 사후 확률)
  3. 2번에서 갱신한 사전확률을 활용하여 사후 확률을 구하면 정확도가 높아짐
• 그림으로 나타낸 정밀도와 재현율
  
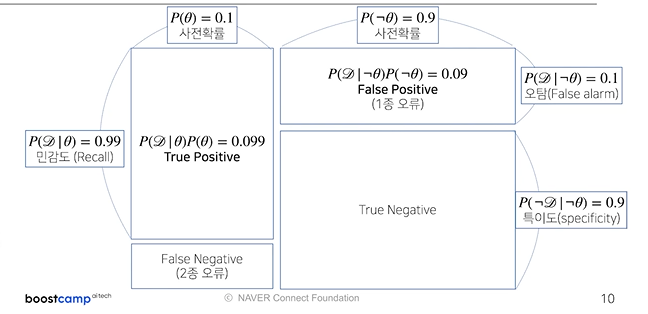
• 사진 출처 : 네이버 부스트캠프 AI Tech 강의