인공 신경망

DONGJIN IM·2022년 4월 25일

AI(NLP) 이론

목록 보기

3/18

MLP(Multi-Layer Perceptron)

신경망(Neural Network)

현실의 복잡한 Data는 선형 모델을 통해서만 처리하기가 매우 힘들다. 따라서, 이런 비선형 Data를 학습시키는 방법이 필요하며, 신경망이라는 개념으로 이 과정이 수행된다
(물론, 신경망을 자세히 뜯어 보면 선형 모델 분석 방식을 중간 과정에서 채택하고 있다.)

신경망이란 Input Data를 Hidden State에 보내고, Hidden State에서 Output Data를 도출해 내는 것으로, Input에서 Hidden state로 보내는 과정, Hidden State에서 Output Data를 도출해 내는 과정에 대한 학습이 요구된다.

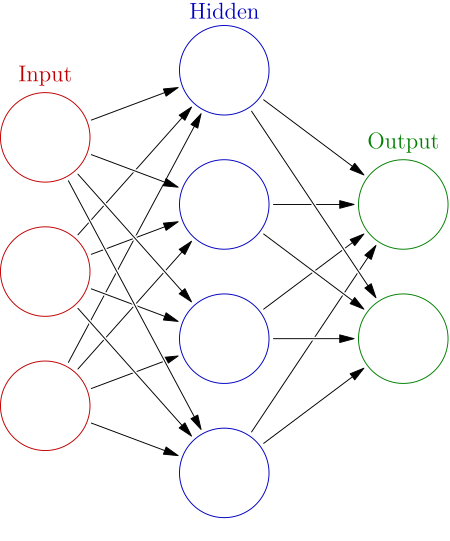
출처 : https://ko.wikipedia.org/wiki/%EC%9D%B8%EA%B3%B5_%EC%8B%A0%EA%B2%BD%EB%A7%9D

신경망에는 1개 Layer마다 학습 대상이 될 Parameter가 존재하며, 이를 활용하여 Input Data(X)로 Hidden Vector들을 형성한다.

만약 Linear Regression이라면, 이 과정에서 $WX^T + b$ 연산이 수행될 것이다.
Hidden Vector들은 선형 관계를 가질 것이며, 가중치 행렬(W)은 Hidden Vector 마다 다르지만, 절편 벡터(b)는 모두 동일하다.

활성 함수

신경망에서 우리는 Hidden Vector가 선형에 가깝다고 했다. 그렇다면 이런 생각이 들 수도 있다.
"그럴거면 걍 선형 모델 분석 방식 쓰지 왜 굳이..."

어찌보면 맞는 말이다. 하지만, MLP에서는 "활성 함수"라는 것이 추가 된다.
이 활성 함수를 선형 모형에 적용시켜, 다시 비선형 모형으로 변환을 시켜 준다.
즉, 계속해서 선형 모델을 학습하는 선형 모델 분석 방식과는 다르게, 비선형 Data를 (신경망을 통해) 선형 모델로 바꾸고, 이 선형 모델을 활성 함수를 통해 다시 비선형 함수로 바꾸고, 그 비선형 Data를 다시 선형 모델로 바꾸는 방식을 반복하며 학습을 진행한다.

즉 활성 함수는 선형 모형을 비선형 모형으로 바꿔주는 비선형 함수라고 할 수 있을 것이다.

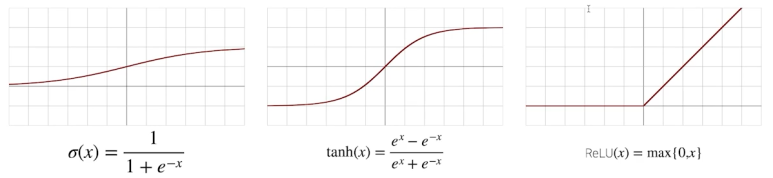
비선형 함수로써 전통적으로는 Sigmoid나 tanh 함수를 많이 활용하였지만, 최근은 ReLU를 많이 활용한다.
하지만, 무조건 ReLU를 활용한다는 것이다. 뒤에서 배우겠지만, 어떤 모델에서는 ReLU를 활용하는 것이 단점으로 작용할 때도 존재한다.

비선형 함수에 대한 그래프

MLP란?

Layer란 1개의 신경망을 말하며, 가중치 행렬 및 절편 벡터로 비선형 Data를 선형 Data로 바꾸는 과정까지라고 생각하면 된다.

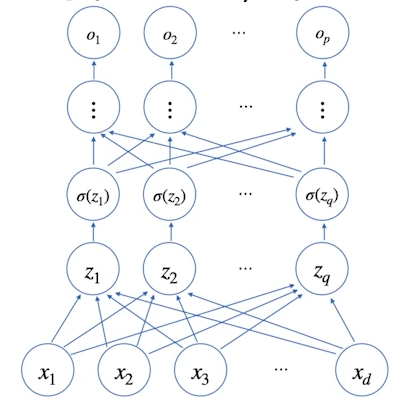
MLP는 Layer가 여러 층 합성된 함수로써 n-Layers 신경망이란 n번의 Layer 과정이 수행되는 신경망을 의미한다.
중요한 점은, 신경망의 Input으로 들어갈 비선형 Data를 활성 함수를 통해 다시 비선형 모델로 만드는 과정이 필수적으로 필요하다.

사진으로 보는 비선형 모델( $\sigma$ : 활성 함수)

그렇다면 왜 층을 여러 개 쌓을까?
결론적으로 말하면 층의 깊이에 비례해 정확도가 좋아지기 때문이다
이유는 아래와 같다.

신경망의 매개변수 수가 줄어듬
층을 깊게 한 신경망은 깊지 않은 경우보다 적은 Parameter를 활용하여 더 높은 수준의 표현력을 달성할 수 있다.
Parameter가 많아지면 그래프가 조금 더 Local Minimum이 많아지게 될 것이며, Data에 Overfitting될 수 있는 확률이 높어진다. 따라서,Parameter 수를 줄여야 하고 이를 위해 가장 많이 활용하는 방법이 층의 깊이를 깊게 하는 것이다
학습의 효율성이 높아짐(학습 Data 양이 덜 필요함)
신경망을 깊게 한다는 것은 그만큼 배울 수 있는 과정이 증가한다는 것이다.
1층 Layer만 존재하면 처음부터 미적분을 배우는 것이지만, Layer가 다양하면 1층에는 사칙연산을, 2층에는 함수를, 3층에는 미적분을 배우는 것처럼 단계별로 학습이 가능하다.
즉, 문제를 계층적으로 분해하여 학습할 수 있으므로 학습 데이터가 적어도 특징을 잘 뽑아내어 학습을 잘 수행할 수 있다
정보를 계층적으로 전달
층을 깊게하면 각 층이 학습해야 할 문제를 풀기 쉬운 문제로 분해할 수 있어 효율적으로 학습이 되는 것을 기대할 수 있다.

Layer가 늘어나면 신경망의 매개변수가 줄어든다는 말이 이해가 되지 않을 수 있다. 어떻게 Layer가 늘어나는데 매개변수가 줄어들 수가 있을까?

예를 들어보자. Convolution을 수행할 때 $5 \times 5$ Filter를 활용할 때 매개변수의 개수는 총 25개가 필요하게 될 것이다.
하지만, $3 \times 3$ Filter를 2개 Layer를 통해 활용하면 연산을 대체할 수 있을 뿐더러, 매개변수 개수는 총 18개만 필요하게 되므로 훨씬 적은 매개변수를 활용하게 된다.

Softmax 연산

(특히 분류문제를 풀 때) 선형 모델을 통해 나온 결과값은 활용할 수가 없다.
선형 모델을 활용하면 값이 음수가 나올 수도 있는데, 분류 문제 같은 경우 (Label이 음수가 아닌 이상) 음수가 나올 수 없으며, 애초에 Label에 속하지 않는 값이 답으로 나올 수도 없다.

위에서 말했듯 신경망은 마지막에 선형 모델을 활성 함수에 집어 넣기는 하지만 결론적으로 분류 문제에 적절한 값이 도출되지는 않는다.
이를 위해 나온 연산 중 대표적인 것이 sofmax이다.

모델의 출력을 확률로 해셕할 수 있게 해주는 대표적인 연산으로, softmax를 통해 Output Data를 확률적으로 계산하여, 해당 Label이 답일 "확률"을 구하는 방법이다.

softmax 연산( $o_1,o_2, ... o_n$ : Hidden Vector에서 도출한 연산 결과값)

softmax(O) = (\frac{e^{o_1}}{\sum _{k\ =\ 1}^pe^{o_k}}, \frac{e^{o_2}}{\sum _{k\ =\ 1}^pe^{o_k}}, ..., \frac{e^{o_p}}{\sum _{k\ =\ 1}^pe^{o_k}})

역전파 알고리즘(BackPropagation)

딥러닝의 학습 원리로, 경사 하강법 등의 Optimizer를 활용하여 가중치나 절편 벡터를 Update하여 학습을 진행하는 방식이다.

Data를 받아 신경망을 통해 원하는 결과를 출력시키는 과정을 순전파(Forward Propagation)라고 하는데, 이와 반대되는 과정이다.

모든 층에 대해서 "윗층부터"(즉, Output과 가까운 Layer부터) 역순으로 학습을 진행하는데, 이 때 Chain Rule과 Loss Function에서 도출한 Loss값을 활용한다.

이 부분은 CNN과 RNN을 배우며 이론적으로 조금 더 자세히 다룰 예정이다.

DONGJIN IM

개념부터 확실히!

이전 포스트

Gradient Descent

다음 포스트