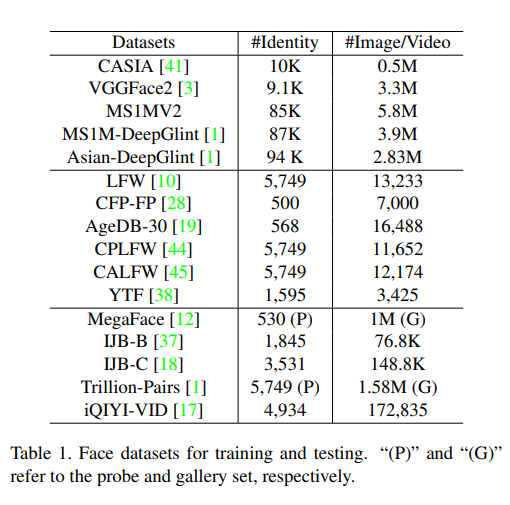
ArcFace: Additive Angular Margin Loss for Deep Face Recognition

Ho Jin Lee·2023년 4월 27일

Face Recognition

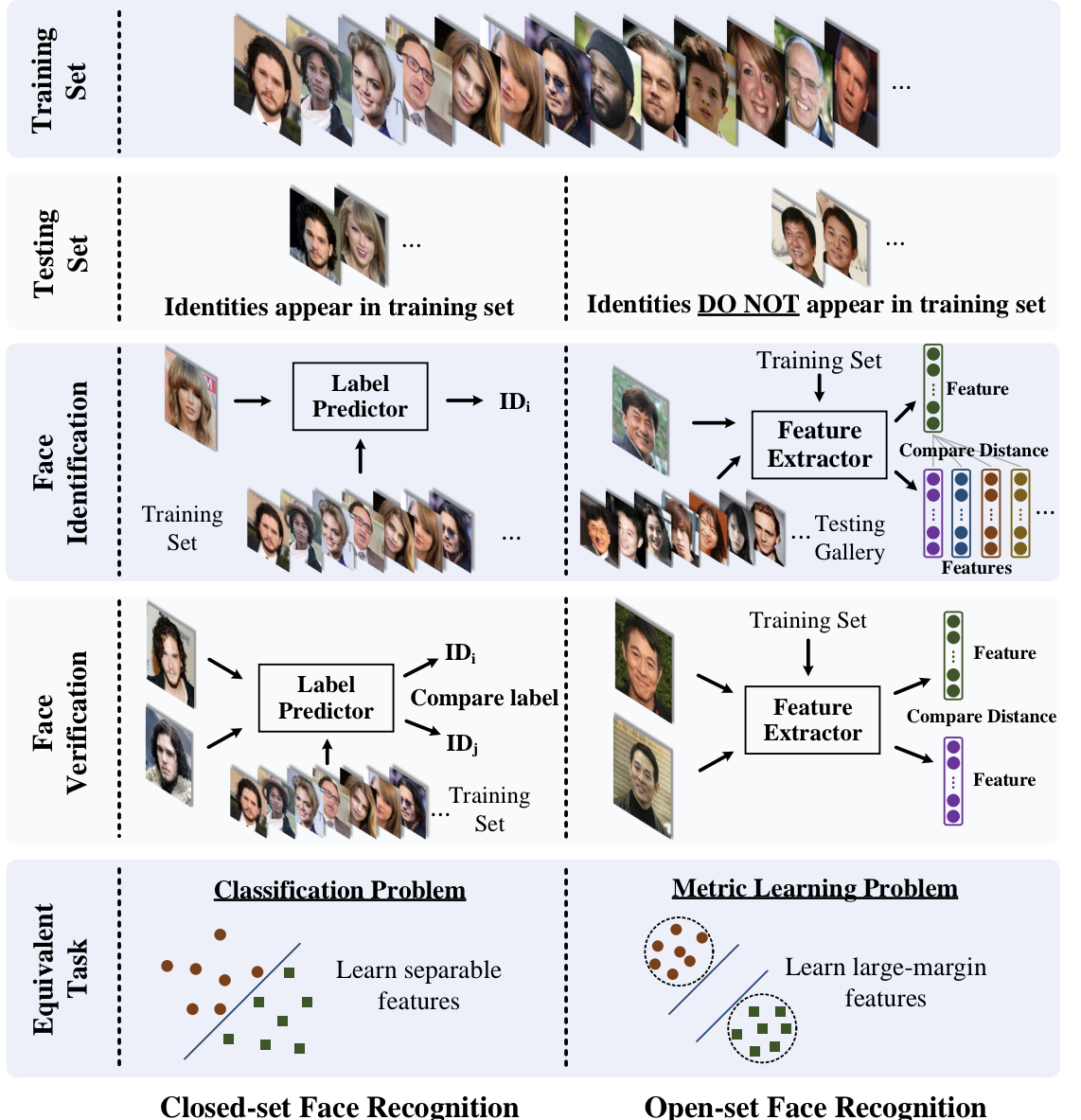
closed set -> 테스트 셋의 클래스가 학습 셋에 동일하게 존재 => 분류 문제!
open set -> 테스트 셋의 클래스가 학습 셋에 존재 X => discriminative하게 학습하는 Metric Learning!!

Abstract

DCNN을 사용한 feature learning(Representation learning) 에서의 문제중 하나 =>

discriminative power 를 증가시킬수 있는 loss function을 설계하는 것.

Centre loss
는 intra-class compactnes를 얻기 위해, deep feature 들과 그 class centres의 유클리디안 공간에서 거리를 penalise 한다. - angular softmax loss, CNN to learn angularly discriminative features.

Sphere Face는
마지막 FC layer 가 angular space의 class center를 나타낸다고 가정. => penalise angles deep feauter와 weights

Additive Angular Margin Loss(ArcFace)
highly discriminative features for face recognition
clear geometric interpretation, due to "exact correspondence to geodesic distance
on a hypersphere"

Introduction

goal of this loss== small intra-class, large inter-class distance

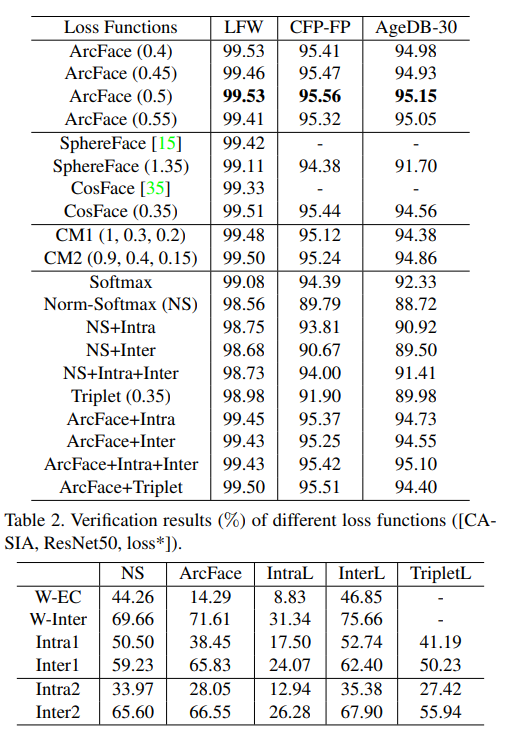
데이터가 충분히 많고, 정교한 DCNN구조를 사용할때 softmax(classification) triplet(metric learning) 모두 괜찮은 성능을 보인다. 하지만 각각의 경우 단점이 존재
softmax(classification):
1. identity의 개수 만큼 마지막 linear transforamtion이 선형적으로 증가한다.
2. closed set의 경우 학습한 feature를 통해 이미지 분류가 가능하지만, open set에서는 충분히 discriminative 하지 않다.
triplet(metric learning)
1. 데이터가 클수록 combinatorial explosion 이 생긴다 => iteration step의 수가 두드러지게 증가한다. (triplet loss는 anchor 라는 기준점과 positive 는 거리가 가깝게, negative 는 거리가 멀게하는 loss)
2. semi-hard sample mining

semi-hard, as they are further away from the anchor than the positive exemplar, but
still hard because the squared distance is close to the anchorpositive distance.

는 어렵다.

softmax 의 discriminative power를 올리려는 시도는 다양하게 있었다. ex centre loss, sphereface,CosFace등.

이 논문에서는 Additive Angular Margin
Loss (ArcFace) 를 제시.

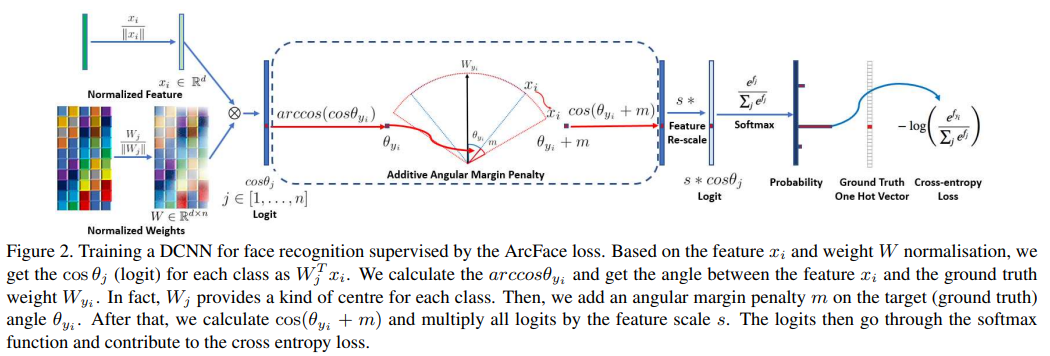
DCNN feature 와 마지막 fully connected layer 의 내적은 the cosine distance after feature and weight normalisation 와 동일하다.

arc cosine 을 통해 current feature 와 target weight사이의 각돌를 계산한다.

그후, additve angular margin을 target angle에 더하고,
cosine으로 다시 target logit을 계산.
fixed feature norm으로 logit들을 rescale. 그후 softmax와 동일한 과정을 거친다.
ArcFace의 장점은 다음과 같다.
Engaging
Effective
SOTA in 10 face recog, benchmarks including large scale image, video datasets
Easy
easy to implement in pytorch, tf and so on, does not need to be combined with other loss
Efficient
only adds negligible compuational complexity .

Proposed Approach

ArcFace

softmax loss

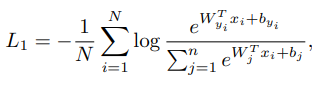
$x_{i}∈ R^{d}$ 는 yi-th class에 속하는 i-th sample의 deep feature를 의미

(embedding feature demension인 d는 512로 되어있다.)

$W_{j}∈ R^{d}$ 는 weight W의 j 번째 column,
$b_{j}∈ R^{n}$ 는 bias term,
N=batch size
n= class number

softmax loss function은 intra class samples들의 higher similarity를 enforce 하지 않기 떄문에 large intra-class appearance variation(포즈, 나이 와같은 차이)에서 performance gap 이 생긴다.

logit을 $W^{T}_{j}x_{i} = ||W_{j}||||x_{i}||cos(θ_{j})$ 로 바꾼다.
$cos(θ_{j})$ 는 weight $W_{j}$ 와 feature $x_{i}$ 사이의 각도.
L2 Norm을 적용해서 $||W_{j}||=1$ 으로 치환

L1 Norm => $\sum_{i}^{n} |x_i|$
L2 Norm => $\sqrt(\sum_{i}^{n} x_i^2)$
s 로 scale
하면 아래식!

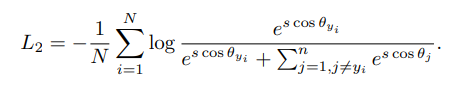
The normalisation step on features and
weights makes the predictions only depend on the angle between the feature and the weight. The learned embedding
features are thus distributed on a hypersphere with a radius
of s

여기서 angular margin penalty m 을 넣어주면 intra class compactness 와 inter class discrepancy를 향상가능!

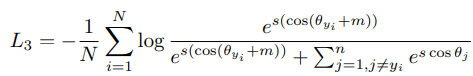
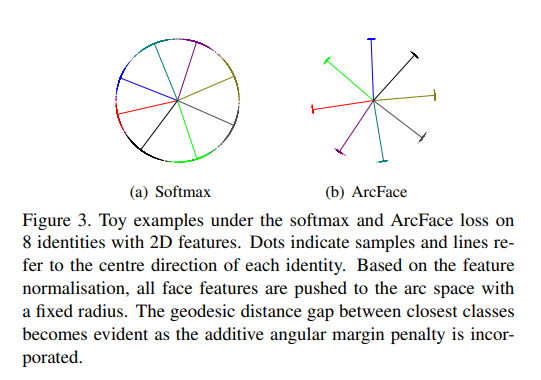
이런느낌으로 arcface 가 더 inter class간 discriminative 하고 intra class compactness를 가지고있따.