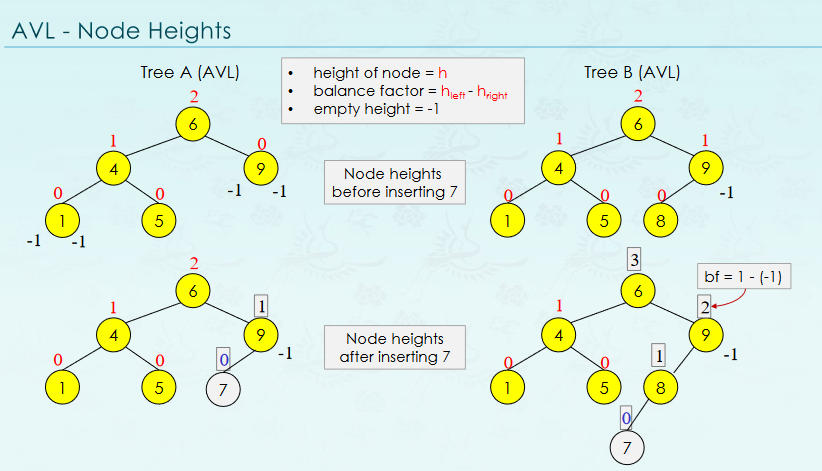
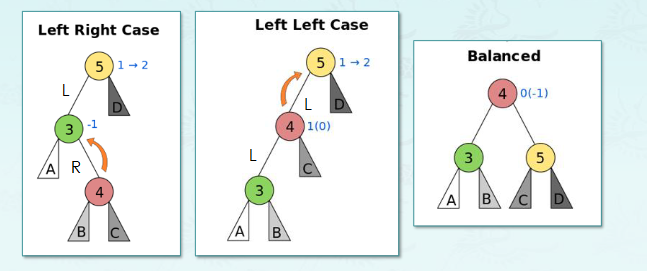
Balance Factor
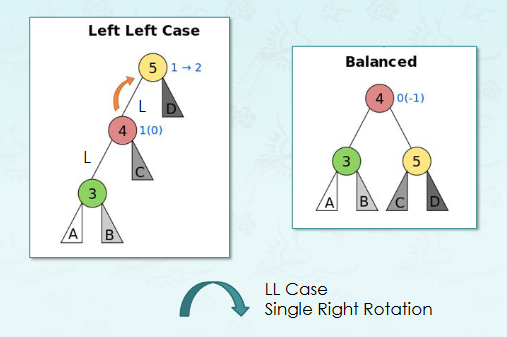
LL case
Right lotation
tree rotateRR(tree A)
{
tree B = A->left;
A->left = B->right;
B->right = A;
return B;
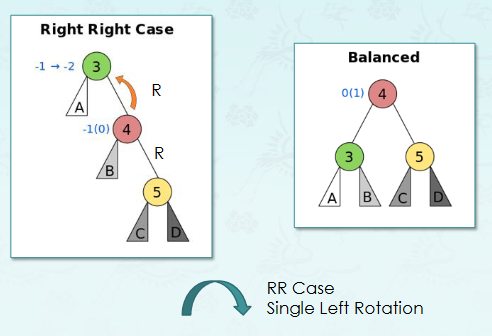
}RR case
Left lotation
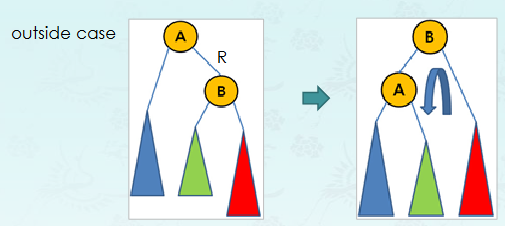
tree rotateRR(tree A)
{
tree B = A->right;
A->right = B->left;
B->left = A;
return B
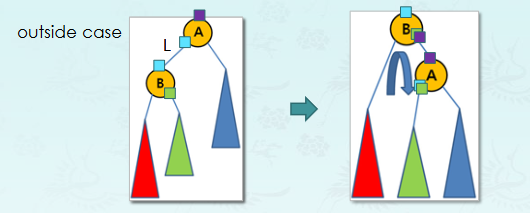
}LR Case
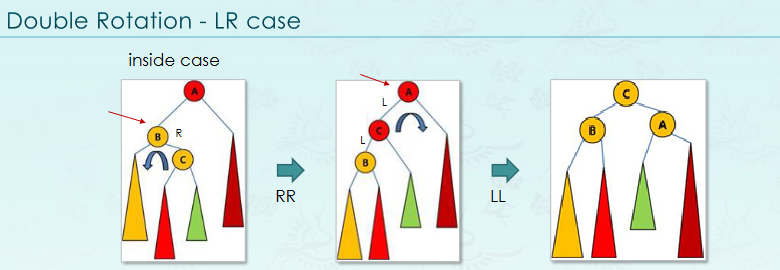
tree rotateLR(tree A)
{
tree B = A->left;
A->left = rotateRR(B);
return rotateLL(A);
}RL case
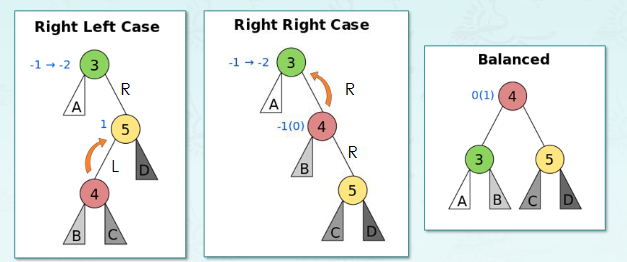
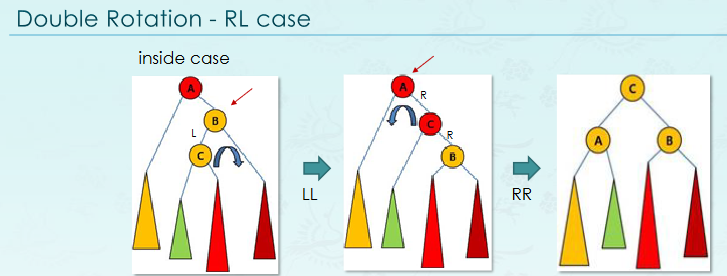
tree rotateRL(tree A)
{
tree B = A->left;
A->right = rotateLL(B);
return rotateRR(A);
}Rebalance
숫자 1,2와 부호에 따라 case가 달라진다.
tree rebalance(tree node) {
if(balanceFactor(node) == 2) // L case
{
if(balanceFactor(node->left) == 1) // LL case
{
node = rotateLL(node);
}
else // LR case
{
node = rotateLR(node);
}
}
else if(balanceFactor(node) == -2) // R case
{
if(balanceFactor(node->right) <= -1) // RR case
{
node = rotateRR(node);
}
else // RL case
{
node = rotateRL(node);
}
}
return node;
}
Height
AVL Tree의 높이가 h가 되기 위해 필요한 최소 노드의 수는 다음과 같다.
𝑛(ℎ) = 𝑛(ℎ − 1) + 𝑛(ℎ − 2) + 1
AVL Tree의 높이가 h는 노드 1.44 ∗ log 𝑛 수를 넘을 수 없다.
h ≤ 1.44 ∗ log 𝑛
Summary

Quiz
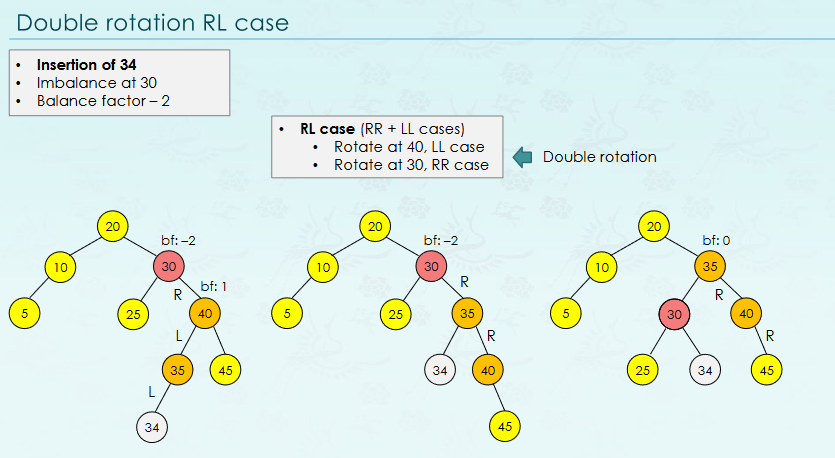
RotationLL(40) -> RotationRR(30)
