DS
1.[DS] Tree introduction
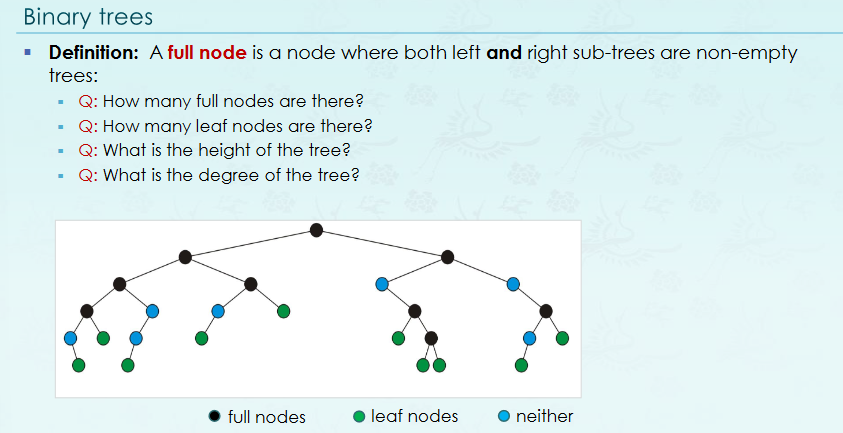
internal node = 자식노드가 하나라도 있는 노드 degree, level은 위에서부터 1 ~ depth는 위에서부터 0 ~ height는 밑에서부터 0 ~ empty node에는 nullptr이 있다. Full binary tree : 2^k-1 이 다
2.[DS] Binary tree Traversal
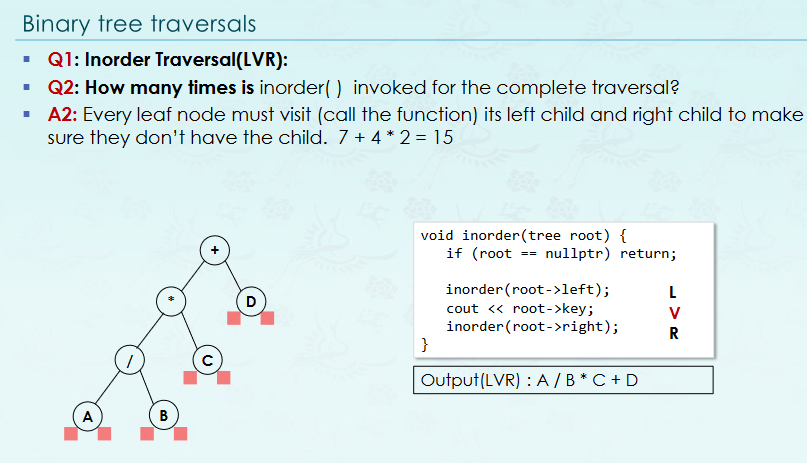
상위 Level부터 하위 Level로 모든 node를 탐색max 값을 판단할 때 반드시 nullptr이 아님을 확인해야 한다.Completry binary tree 형식이 되도록, level order 순으로 node를 추가한다.
3.[DS] Binary Search Tree
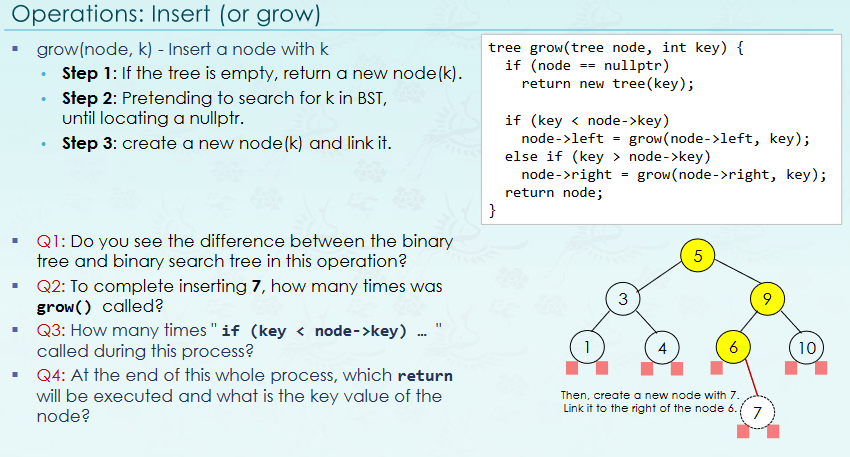
해당 노드를 nullptr 처리함해당 노드를 지우기 전에 Child를 해당 노드의 부모노드와 link 시킨 후 제거predecessor(왼쪽의 Max) or successor(오른쪽의 Min) 중 height가 가장 높은 것을 골라 해당 값을 지우려는 노드에 덮어 씌우
4.[DS] AVL Tree
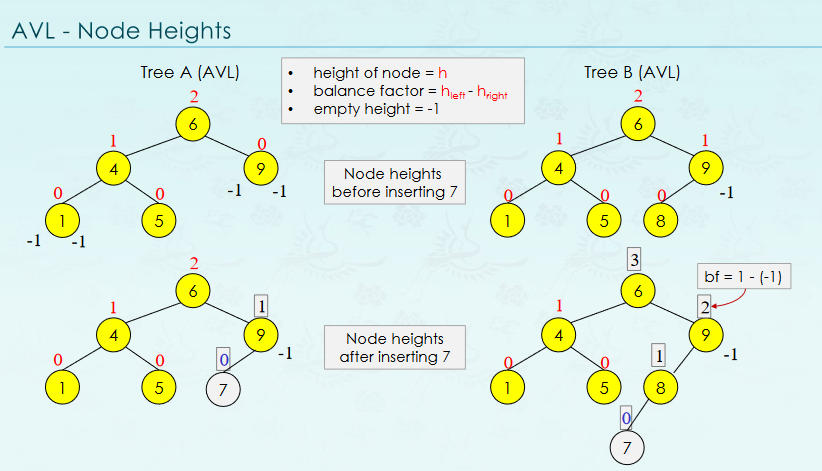
Right lotationLeft lotation숫자 1,2와 부호에 따라 case가 달라진다.AVL Tree의 높이가 h가 되기 위해 필요한 최소 노드의 수는 다음과 같다.𝑛(ℎ) = 𝑛(ℎ − 1) + 𝑛(ℎ − 2) + 1 AVL Tree의 높이가 h는 노드
5.[DS] Heap

Heap Priority queue Min Heap Root가 Min이다 아래로 갈 수록 node 값이 커짐 Max Heap Root가 Max이다 아래로 갈 수록 node 값이 작아짐 Swim max heap인 경우 부모가 현재 노드보다 작으면 계속 올라가야 하
6.[DS] Graph
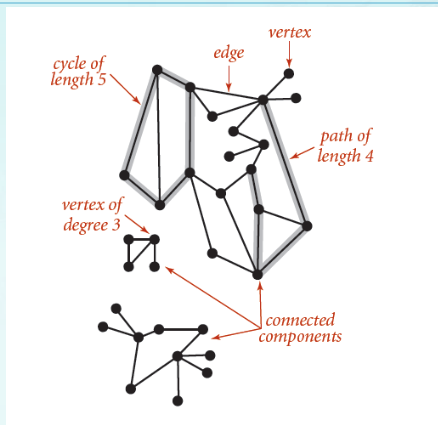
set of vertices connected pairwise by edgesmemory loss가 있음각 노드와 연결된 vertices들을 linked list 형태로 저장새로 Edge를 추가할 때, 두 노드를 양방향으로 연결해주어야 한다Edge를 추가하는 아래 함수