Heap

Priority queue

Min Heap

Root가 Min이다
아래로 갈 수록 node 값이 커짐

Max Heap

Root가 Max이다
아래로 갈 수록 node 값이 작아짐

Swim

max heap인 경우 부모가 현재 노드보다 작으면 계속 올라가야 하므로
comp가 less(p, k/2, k)이고, q[k/2] < q[k]

min heap인 경우 부모가 현재 노드보다 크면 계속 올라가야 하므로
comp가 more(p, k/2, k)이다. q[k/2] > q[k]

void swim(heap p, int k) 
{	
	// 
	while(k > 1 && p->comp(p, k/2, k))
	{
		swap(p,k/2,k);
		k = k / 2;
	}
}

Sink

max heap인 경우 현재 노드가 자식 노드보다 작으면 계속 내려가야 하므로
comp가 반대인 more(p, k/2, k)이고, q[k/2] > q[k]

min heap인 경우 부모가 현재 노드보다 크면 계속 올라가야 하므로
comp가 less(p, k/2, k)이다. q[k/2] < q[k]

void sink(heap p, int k) 
{	
	while(2*k <= p->N)
	{
		int j = 2*k; 
		// max heap인 경우 자식 노드가 둘 중 더 큰 것을 target
		// min heap인 경우 자식 노드가 둘 중 더 작은 것 target
		if(j<p->N && p->comp(p,j,j+1)) 
			j++;
		// k node가 max heap을 만족한 경우  break
		// k node가 min heap을 만족한 경우 break
		if(!(p->comp(p,k,j)))
			break;
		swap(p,k,j);
		
		k = j;
	}
}

Insert

Insert: Add node at end, then swim it up.

void grow(heap p, int key) 
{
	(p->N)++;

	if(p->N == p->capacity)
		reserve(p, p->capacity*2);

	p->nodes[(p->N)] = key;	
	swim(p, p->N);
	
    return;
}

Delete (pop)

Heap은 Queue이므로 Root가 Delete을 하게 되면 Root가 pop이 된다.
Remove: Swap root with last node, then sink down

void trim(heap p) 
{
	if (empty(p)) return;

	swap(p,1,p->N);
	p->N--;

	if(p->N == (p->capacity)/4 && p->capacity > 4)
		reserve(p, (p->capacity)/4);

	sink(p,1);
}

Heap Sort

heapify

last internal node = n/2 부터 1번 node까지의 노드들을 sink

void heapify(heap p) 
{
	// This is O(n) algorithm
	int n = p->N;

	for(int i=n/2; i>=1; i--)
	{
		sink(p, i);
	}
}

sorting

전체 사이즈를 하나씩 줄여가며 root와 마지막 노드를 바꾼 후
root 노드를 sink한다.

전체 과정이 끝나면, heap size를 원래대로 돌린다.

void heapsort(heap p) {
		
	heapify(p);

	int save_N = p->N;

	for(int i=p->N; i>=1; i--)
	{
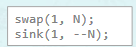
		swap(p,1,p->N);
		p->N--;
		sink(p,1);
	}
	p->N = save_N;
	
}

heap to binary tree

1. Create the tree (root) node with the first key from CBT (or nodes[1]).
2. Enqueue the root node.
3. Loop through from the CBT nodes[2] to nodes[N]
   A. Make a new node from nodes[].
   B. Get a tree node in the queue.
   C. If the left of the tree node doesn’t exist,
   set the new node to the left of the tree node.
   else if the right of this tree node doesn’t exist,
   set the new node to the right of the tree node.
   D. If this tree node is full, pop (or dequeue) it.
   E. enqueue the new node (to add children later if any).
4. treeprint(root)