Graph

set of vertices connected pairwise by edges

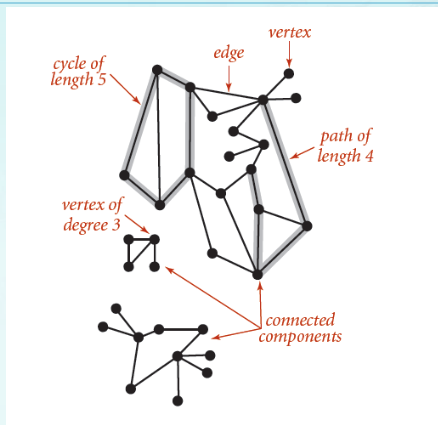
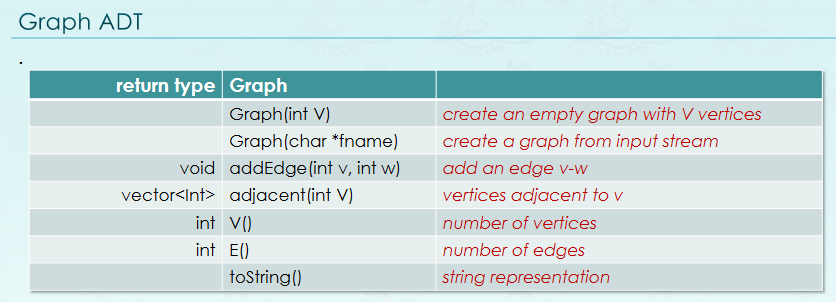
Graph

struct Graph {
  int V; // N vertices
  int E; // N edges
  gnode adj; // array of linked lists of vertices
  
  Graph(int v = 0) 
  { // constructs a graph with v vertices
    V = v;
    E = 0;
    adj = new (nothrow) Gnode[v];
    assert(adj != nullptr);
    for (int i = 0; i < v; i++) 
    { 
    // initialize adj list as empty;
      adj[i].next = nullptr;
      adj[i].item = i;
  	}
  }
  ~Graph() {}
};
using graph = Graph *

Vertice (Linked List)

struct Gnode 
{
  int item;
  Gnode* next;
  Gnode (int i, Gnode *p = nullptr) 
  {
  	item = i; next = p;
  }
  ~Gnode() {}
};

using gnode = Gnode *;

Euler path

Hamilton cycle

Graph Constructure

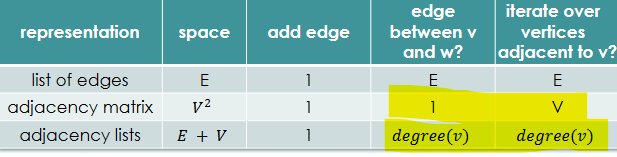
Adjacency - Edge list

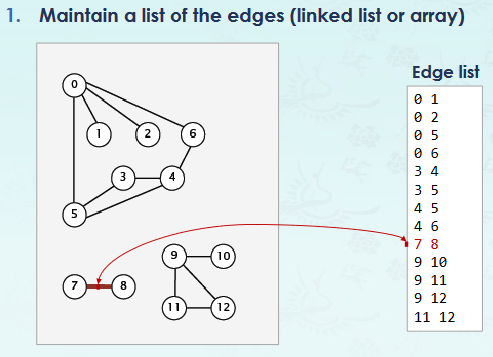
Adjacency - Maxtrix

memory loss가 있음

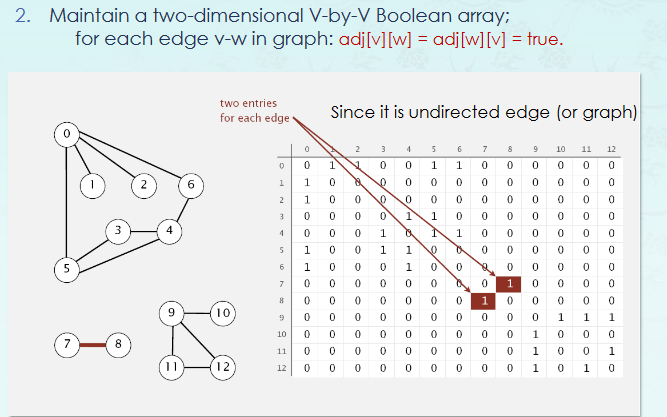
Adjacency - List

각 노드와 연결된 vertices들을 linked list 형태로 저장

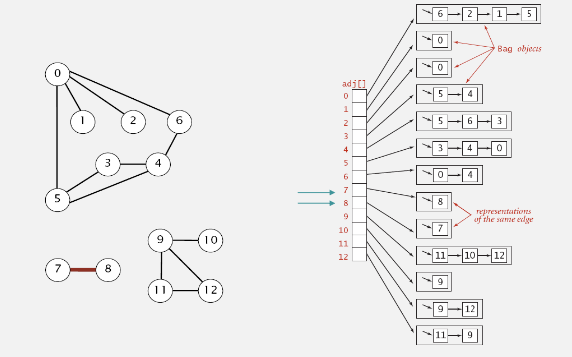
Graph Function

degree of v

int degree(graph g, int v) 
{
  if (!validVertex(g, v)) return -1;
  int deg = 0;
  
  for (gnode w = g->adj[v].next; w; w = w->next, deg++);
  
  return deg;
}

max degree

int degree(graph g) 
{
  int max = 0;
  for (int v = 0; v < V(g); ++v) 
  {
    int deg = degree(g, v);
    if (deg > max) max = deg;
  }
  return max;
}

degree_avg

double degree_average(graph g) 
{
	int return 2.0 * E(g) / V(g);
}

void addEdgeFromTo Problem

새로 Edge를 추가할 때, 두 노드를 양방향으로 연결해주어야 한다

void addEdge(graph g, int v, int w) 
{
  addEdgeFromTo(g, v, w); // edge from v to w
  addEdgeFromTo(g, w, v); // since undirected
}

Edge를 추가하는 아래 함수를 사용하게 될 경우,
node를 연속으로 추가하게 되면 노드가 추가가 되지 않고,
g->adj[v].next 부분에 노드가 계속해서 덮어쓰기 되는 현상이 발생한다

void addEdgeFromTo(graph g, int v, int w) 
{
  gnode node = new Gnode(w);
  g->adj[v].next = node;
  g->E++;
}

따라서 위 함수를 다음과 같이 수정해주어야 한다

void addEdgeFromTo(graph g, int v, int w) 
{
  gnode node = new Gnode(w, g->adj[v].next);
  g->adj[v].next = node;
  g->E++;
}

새로운 노드를 뒤에서 추가하게 되면 time complexity가 증가하므로 g->adj[v].next를 새로운 노드로 설정하고 새로 추가된 노드 뒤에 기존 노드들을 연결하는 방식으로 함수를 변경하면 덮어쓰기 문제가 해결된다

DFS

Depth-First Search

Recursively visit all unmarked vertices adjacent to v.
Put unvisited vertices on a stack.

• boolean[] : 해당 vetice를 방문했는지 check
• int[] parent : 해당 vetice를 어디서 통해 방문했는지 저장
• (parent[w] == v) : w가 v를 통해서 처음 방문되었음을 의미

void DFS(graph g, int v, queue<int>& que) 
{  	
	g->marked[v] = true;	// visited
	que.push(v);			// save the path
	
	for(gnode w = g->adj[v].next; w; w = w->next) // linked list search
	{		
		if(g->marked[w->item] == false)
		{
			DFS(g, w->item, que);
			g->parentDFS[w->item] = v;
		}
	}
}

BFS

Breadth-first search demo

Repeat until queue is empty

Remove vertex v from queue
Add to queue all unmarked vertices adjacent to v and mark them

Put unvisited vertices on a queue

void BFS(graph g, int v) {
	queue<int> que;		  // to process each vertex
	queue<int> sav;       // BFS result saved

	// all marked[] are set to false since it may visit all vertices
	for (int i = 0; i < V(g); i++)  g->marked[i] = false;
	
	g->parentBFS[v] = -1;
	g->marked[v] = true;
	g->distTo[v] = 0;
	g->BFSv = {};         

	que.push(v);
	sav.push(v);

	while (!que.empty()) 
    {
		int cur = que.front(); que.pop();  // remove it since processed
		
		for (gnode w = g->adj[cur].next; w; w = w->next) 
        {
			if (!g->marked[w->item]) 
            {
				g->marked[w->item] = true;
				que.push(w->item);			// queued to process next
				sav.push(w->item);			// save the result
				
				g->parentBFS[w->item] = cur;
				g->distTo[w->item] = g->distTo[cur] + 1; // set parentBFS[] & distTo[]
			}
		}
	}

	g->BFSv = sav;                // save the result at v
	setBFS0(g, v, sav);
	DPRINT(cout << "<BFS v=" << v << endl;);
}

BFS Properties

BFS에서 s to v search를 할 때, 시간 복잡도는 E(간선 수)+V(vertex) 수에 비례하고, DFS보다 shortest path를 찾는데에 적절하다.