Introduction

ICASSP 2024에 게재된 Alexander H.Liu et al.의 논문 REVISITING SELF-SUPERVISED LEARNING OF SPEECH REPRESENTATION
FROM A MUTUAL INFORMATION PERSPECTIVE은 Self-Supervised Learning 모델의 성능을 표현하는 generic, task-independent한 metrics를 Mutual Information 차원에서 만들고자 한다.

기존의 SSL 모델은 그 학습 방식이 어떻든 (APC, MLM, ... ), 그 모델 구조가 어떠하든 상관없이 평가를 위해서 Downstream tasks에 적용했을 때의 성능을 사용한다. Speech라면 Linear Probing (Pretrained 된 SSL 모델에 Linear Layer만 추가로 넣어서 Classification, Phonetic Recognition 등을 수행하는 것) 등을 활용하거나 Speech Recognition, Audio Classification, Sound Event Detection 등의 태스크에서 모델이 어떠한 성능을 발휘하는지 평가하는 방식으로 실험하곤 한다.

하지만 상기한 방법론은 SSL 모델을 평가하는데 있어 치명적인 단점을 세 가지 가진다. 바로 (1) SSL 모델은 General한 representation을 만드는 데 집중해야 하는데 Downstream tasks는 모두 specific 하기 때문에 SSL 자체의 중요성이 큰 맥락과 어울리지 않다는 점과 (2) SSL 모델의 형성 방식 (학습 방식, 모델 디자인 등) 이 Downstream tasks에 적합하지 않다면 특정 downstream tasks에 대해 좋지 않은 성능을 낼 수도 있다는 점, 마지막으로 (3) 평가 방식으로 흔히 기용되는 Linear Probing 이 output dimension (= label size) 에 그 성능이 불필요하게 크게 좌우된다는 점이 있다. (2)은 특히 중요한데, 오디오 분야에서 어려운 태스크는 음성 인식, TTS 와 같이 여러 모달리티를 융합하거나 high-level features를 담아야 하는 것이 있겠고, 쉬운 태스크로는 audio enhancement, audio classification 등이 있겠다. 사용하는 데이터의 형태에 따라, 모델의 생김새에 따라 어떤 태스크는 잘 풀지만 어떤 태스크는 잘 풀지 못할 가능성이 있다.

따라서 본 논문은 Mutual Information(이하 MI) 의 관점에서 downstream tasks나 label 등에 관계 없이 Unlabeled data 자체만을 가지고 speech SSL 모델의 성능을 평가하고자 한다.

Methodologies

Speech SSL 모델은 Input audio data $X$를 받아서 general representation인 $Z$를 만들어 낸다. 이 general representation $Z$는 해결하고자 하는 문제 (ex. downstream tasks)를 풀기 위해 많은 정보를 가지고 있어야 하는데 이는 MI의 차원에서 설명이 가능하다.

Bounding MI with labeled data

먼저 기존의 방법론들이 Labeled data를 바탕으로 모델의 MI, 즉 성능을 어떻게 평가했는지 살펴보자. 우리는 $MI(Z;Y)$, 즉 labeled data $Y$와 general representation $Z$가 얼마나 많은 정보를 공유하고 있는지 알고 싶다.

위 수식에서 $q_{\omega}$는 downstream tasks 에 적용하는 auxillary prediction model에 $Z$를 추가로 학습시킨 결과이다. 즉 $MI(Z;Y)$를 정확히 알지는 못하지만, 이를 기존에 데이터를 통해 구할 수 있는 라벨의 엔트로피 $H(Y)$에서 Downstream tasks에 적용했을 때 $Z$가 $Y$를 풀 수 있는 정도인 엔트로피 $E(-logq_{\omega}(y|z))$를 뺀 값이 그 Lower Bound로서 작동하게끔 유도할 수 있다. 더 자세한 설명은 생략한다.

사실 SSL 모델을 평가하는 지표나 실험결과들은 $E(-logq_{\omega}(y|z))$ 차원에서 그치지만, 이를 MI의 차원에서 보면 MI의 Lower Bound를 제공하는 하나의 clue로서의 역할을 한다는 것이다.

서론에서 언급했듯 이 $q_{\omega}$ operator는 다양한 문제를 갖고 있기 때문에 (Label dependence, task dependence 등) 이제는 unlabeled data 상황에서 MI의 lower bound를 어떻게 제공할 수 있는지, 즉 이 논문이 어떠한 contributions를 해 냈는지 살펴보자.

Bounding MI with unlabeled data

과정은 다음과 같다. 하나의 speech input에서 두 개의 다른 section을 뽑아 각각 $X_a$, $X_b$로 저장한다. 이들을 SSL 모델에 input으로 넣어 각각 latent representation인 $Z_a, Z_b$를 만든다.

위의 식은 MI의 성질에 따른 것이다. 즉 marginal entropy 에서 conditional entropy를 빼면 MI가 된다는 것. 하지만 $H(Z_a|Z_b)$를 직접 구하기란 여간 쉽지 않다. 따라서 $Z_b$를 empirical(calculable)하게 만들기 위해 새로운 cluster 함수 $f_{cluster}$을 고려한다. cluster 함수를 추가하는 과정에서 정보가 아무래도 더 왜곡될테니 (quantize, simplify) 그 때의 MI는 기존보다는 더 낮아질 것이다. 그러면 아래의 수식이 생긴다. (논문에서는 심플하게 k-means를 써서 클러스터링을 수행한다.)

이는 entropy의 정의에 따라 아래의 lower bound를 형성한다.

$H(f_{cluster}(Z_b))$는 데이터만 있으면 금방 계산할 수 있다. 또한 뒤 식에 있는 $q_{\omega}$는 앞서 정의한 Linear probing의 일종으로, $Z_a$를 바탕으로 $Z_b$의 cluster를 예측하는 과정이다. 지극히 label-free한 과정이라고 볼 수 있다.

Experimental Results

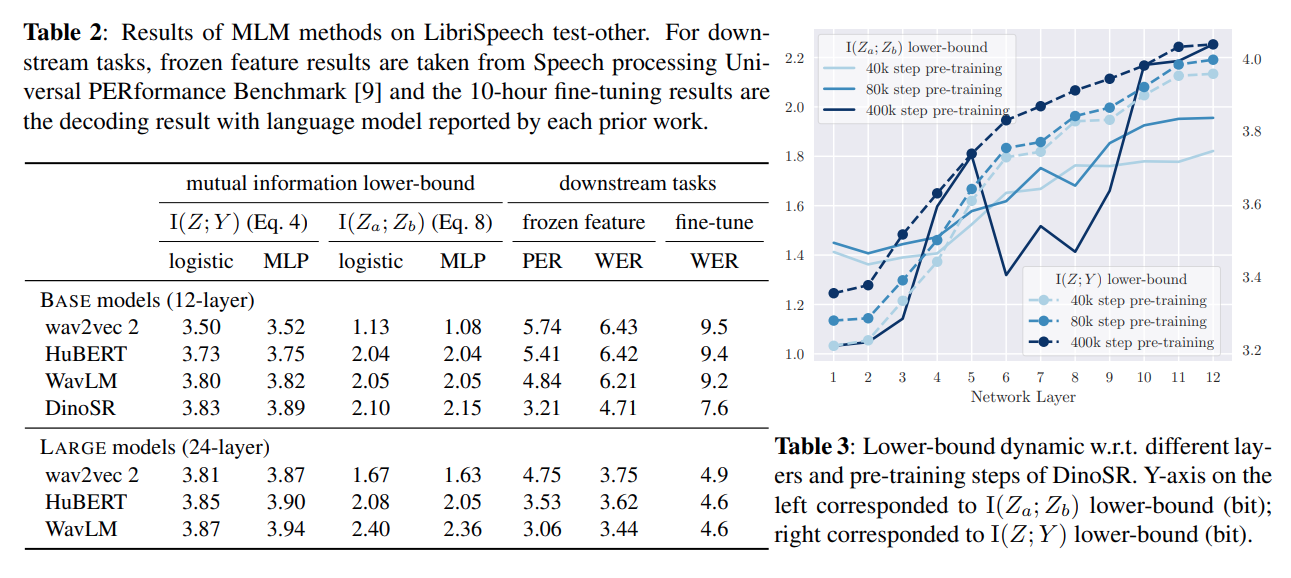
결과를 보자. Mutual Information lower-bound가 높을 수록 모델이 general representation을 잘 만드는 것이다. 놀라운 것은, general representation power가 높을수록 downstream tasks (여기에서는 Speech recognition) 에 대한 적응력이 높았다는 점이다. 특정 태스크에적절하게 사용하기 위해서 모델 구조나 학습 방식을 설정하는 것보다, 정말로 'general'한 representation으로부터 시작하는 것이 좋은 SSL 모델을 만드는 key factor라는 인사이트를 얻을 수 있겠다.

Contributions & Limitations

이 논문은 먼저 output dimension에 의존한다고 했던 linear probing의 문제를 저자가 꼬집은 것에 반해, 이와 유사한 방식으로 (클러스터링 및 예측) lower-bound를 만들어서 역시 label dimension에 robust하지 못한 예측을 했다는 점이 한계점이다.

하지만 general representation power를 평가하는 단일화된 평가 지표를 만들었다는 점과, 그 과정에서 논리적 허점이 없고 그 결과 역시 예상과 같다는 점에서 직관적이고 잘 이해되게 실험을 잘 한 것 같다.