KNN, K-Means

인화·2026년 1월 1일
KNNk-means

인공지능

목록 보기
7/7

kNN 알고리즘 (k-Nearest Neighbor)

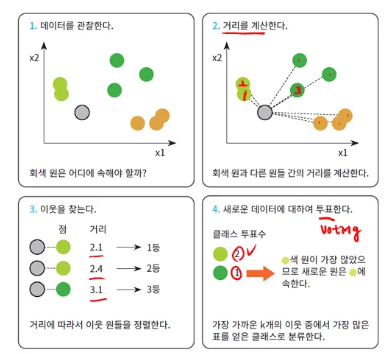
 kNN(k-Nearest Neighbor) 알고리즘은 k개의 가장 가까운 이웃 데이터를 찾고, 그 이웃들의 레이블을 기반으로 분류/회귀 문제를 해결하는 알고리즘을 의미한다.

 kNN 알고리즘은 새 데이터가 입력으로 들어오면, 이 포인트가 어떤 클래스에 속해있는지를 찾는다. 이를 위해 k개의 이웃을 찾고, 이웃 중 가장 많은 클래스에 속한 레이블을 해당하는 데이터 포인트에 속하는 클래스라고 지정한다. 이때, k 값에 따라 결과가 달라질 수 있으며, 데이터의 분포와 패턴이 명확할 때 더 잘 작동하는 경향이 있다. k 값은 일반적으로 홀수를 선택한다. (짝수로 선택하게 되면 Voting 시 동점이 발생할 수 있기 때문이다.)

 kNN 알고리즘은 데이터 포인트가 가장 많이 속한 클래스로 분류를 수행한다. 따라서 특징 공간에 있는 모든 데이터에 대한 정보가 필요하다. 이러한 점 때문에 모든 학습 데이터를 저장해야 해서 메모리의 양이 크고, 기존 모든 포인트와의 모든 거리를 계산해야 해서 계산 복잡도가 크다는 문제점이 있어 데이터와 클래스가 많을수록 효율성이 낮아진다. 하지만, 직관적이고 이해하기 쉬우며, 사전 학습 시간(학습 시간)이 필요하지 않다는 장점이 있다.

  • 핵심 : 거리 기반 이웃 찾기, kNN은 학습하는 알고리즘이 아니다! 거리 기반 계산임.

  • 정의 : 새로운 샘플 x에 대해 학습 데이터의 가장 가까운 k개 이웃의 다수결(분류) 또는 평균(회귀)으로 예측하는 비모수, 메모리 기반(lazy) 알고리즘

    • 비모수(non-parameter) : 모집단이 특정 분포를 따른다는 가정을 하지 않고 통계적 분석을 하는 방법. 다시 말해, 데이터의 분포나 함수 형태에 대해 특정한 가정을 두지 않는 것.
    • 예를 들어 선형 회귀 모델의 경우엔 y=ax+by=ax+b와 같이 미리 정해진 형태를 가정하므로 모수적이다. 하지만, kNN은 모델 파라미터가 고정되어 있지 않고, 어떠한 함수 형태나 파라미터를 학습하지 않으므로 비모수적이라고 할 수 있다.

  • 거리 척도 : 기본은 유클리드 거리(ℓ2ℓ_2)임. 대안 : 맨해튼(ℓ1ℓ_1), 민코프스키(ℓpℓ_p), 코사인 등.

d(x,xi)=∑j=1d(xj−xij)2d(\mathbf{x}, \mathbf{x_i}) = \sqrt{\sum_{j=1}^{d} (x_j - x_{ij})^2}
  • 가중 kNN : weights='distance'로 가까운 이웃에 더 큰 가중치를 부여하는 것
  • 하이퍼파라미터 : k, metric(거리 측정 방법), weights(가중치 결정 방법, uniform - 동일 가중치, distance - 거리에 반비례하는 가중치), p(민코프스키 차수)
    • weights를 distance로 부여하면, 거리에 반비례하는 가중치를 부여하므로 예측값은 더 가까운 이웃에 더 큰 영향을 받게 됨. (가까운 거리에 더 큰 가중치를 부여하게 되므로)
    • Bias-Variance Trade-off : k↓ → 경계 세밀(분산↑, 과적합), k↑ → 경계 매끈 (편향↑, 과소적합)
    • 전처리 : 거리 기반이므로 스케일 영향이 큼 → 표준화/정규화 권장
    • 복잡도 : 학습 비용 작음, 예측 시 O(n⋅d)O(n⋅d)
      • 대량 데이터면 KD-Tree/볼-트리/근사 최근접 탐색 고려
  • 유클리드 거리 : 각 차원의 차를 제곱해서 사용하는 것으로, n차원에서 두 점 사이의 거리를 구할 경우 다음과 같이 나타냄.
(a1−b1)2+(a2−b2)2+⋯+(an−bn)2\sqrt{(a_1 - b_1)^2 + (a_2 - b_2)^2 + \cdots + (a_n - b_n)^2}
  • 맨해튼 거리 : 각 차원의 차를 제곱해서 사용하는 것이 아닌, 절댓값을 바로 합산하는 것을 의미하며, 맨해튼 거리는 항상 유클리드 거리보다 크거나 같다.
∣a1−b1∣+∣a2−b2∣+⋯+∣an−bn∣|a_1 - b_1| + |a_2 - b_2| + \cdots + |a_n - b_n|
  • 민코프스키 거리 : 유클리드 거리와 맨해튼 거리를 일반화한 거리로, 차이의 절댓값에 거듭제곱을 취하고 다시 루트를 적용한 형태임.
    • p=1일 경우 맨해튼 거리, p=2일 경우 유클리드 거리, p=∞\infty일 경우 체비쇼프 거리와 동일함.
(∣a1−b1∣p+∣a2−b2∣p+⋯+∣an−bn∣p)1p(|a_1 - b_1|^p + |a_2 - b_2|^p + \cdots + |a_n - b_n|^p)^{\frac{1}{p}}
knn = KNeighborsClassifier(n_neighbors=6)
knn.fit(X_train, y_train)

y_pred = knn.predict(X_test)
scores = metrics.accuracy_score(y_test, y_pred)
# kNN은 전처리의 영향을 많이 받는다.
# 표준화 전이 표준화 후보다 성능이 더 높음.
# 표준화는 무조건 해야 한다 X, 성능을 보고 무엇(하는 것 or 안 하는 것)이 더 좋은지 판단해야 함.
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import cross_val_score, KFold

# shuffle은 데이터를 섞는 것으로, 학습 시 순서에 의존하는 것을 방지해줌.
cv = KFold(n_splits=5, shuffle=True, random_state=42) # n_splits=5이므로 5-Fold CV
raw_model = KNeighborsClassifier(n_neighbors=5)

# cross_val_score(estimator, X, y, cv=None) : 교차 검증을 통해 점수를 평가하는 교차 평가 함수
score_raw = cross_val_score(raw_model, X, y, cv=cv).mean() # 정규화 전 CV Score

# 파이프라인이란, 전처리 → 학습 → 평가로 이어지는 일련의 과정들을 하나로 묶는 것임.
pipe = Pipeline([('scaler', StandardScaler()), ('knn', KNeighborsClassifier(n_neighbors=5))]) # 정규화 후 knn
score_scaled = cross_val_score(pipe, X, y, cv = cv).mean() # 정규화 후 CV Score

print("CV 정확도 (무스케일) : ", score_raw)
print("CV 정확도 (표준화) : ", score_scaled)

머신러닝 성능 평가

Confusion Matrix (혼동 행렬)

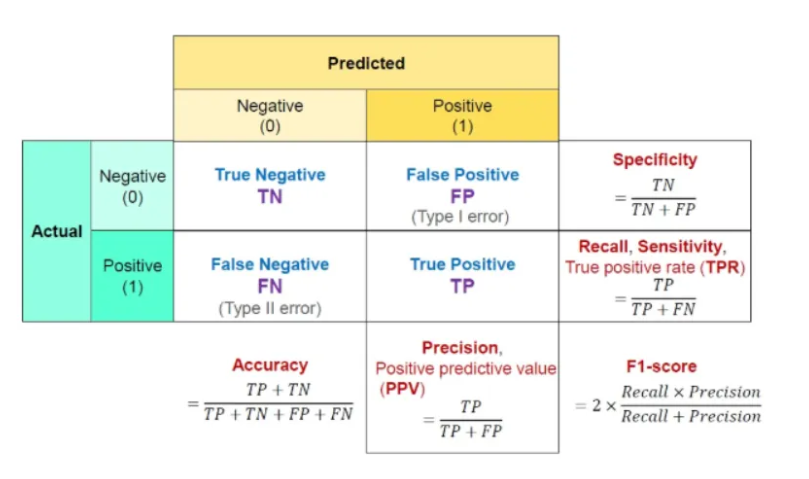
  • 혼동 행렬 : 예측값과 실제값 사이 관계를 행렬 형태로 표현한 것
  • F1 Score는 정밀도와 재현율의 조화평균을 의미하며, 한쪽 클래스에 치우친(클래스 편향이 있을 때) 예측 성능을 과대평가하지 않도록 하여 불균형 데이터에서의 평가 편향을 완화한다. (→ 편향된 모델을 좋은 모델로 평가하지 않는다)
  • 정밀도와 재현율 중 하나라도 작으면, 그 값의 역수가 커져 조화평균(F1)이 크게 감소한다. F1은 Precision과 Recall 중 작은 값에 의해 지배된다.
  • 조화 평균은 역수의 산술평균의 역수를 의미한다. 역수의 차원에서 평균을 구하고, 다시 역수를 취해 원래 차원의 값으로 되돌리는 것이다. x=2aba+bx = \frac {2ab}{a+b}와 같이 표현한다.

결과 해석

  • 정확도 : 전체 문제 중에서 정답을 맞춘 비율
    • Accuracy = TP + TN / TP + TN + FP + FN
  • 정밀도 (Precision) : True라고 분류한 것 중 실제로 True인 것의 비율 (Positive 정답률)
    • Precision = TP(True Positive) / (TP(True Positive) + FP(False positive))
  • 재현율 (Recall) : 실제 True인 것 중에서 True라고 예측한 것의 비율
    • Recall = TP(True Positive) / (TP(True Positive) + FN(False Negative))
    • Sensitivity 혹은 Hit Rate라고도 불림.
  • F1-score : Precision과 Recall은 상호보완적이기 때문에, Recall을 올리면 Precision이 내려가고, Precision을 올리면 Recall이 내려갈 수 밖에 없다. 이를 보완하기 위해 생겨난 것이 Recall과 Precision의 조화평균인 F1 score이다.
    • Precision과 Recall의 조화평균으로 0.0~ 1.0 사이의 값을 가지며, 값이 1에 가까울수록 좋은 모델이다.

분류 리포트

  • macro avg : 각 클래스의 성능 지표를 동일한 가중치로 평균한 값
    • 모든 클래스를 동일하게 중요하게 취급하므로 클래스 불균형이 심하면 낮게 나오는 경향
  • weighted avg : 각 클래스 성능을 해당 클래스 샘플 수(support)로 가중 평균
    • 데이터 분포를 반영한 평균이므로 클래스 불균형에 둔감함.
# Confusion Matrix를 판단할 땐, 대각 성분을 봐야 한다.
# Confusion Matrix의 x축은 모델, y축은 정답을 의미함.
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.metrics import ConfusionMatrixDisplay

digits = load_digits() # 데이터 로드
n_samples = len(digits.images) # 데이터 개수
# knn은 이미지 형태 그대로 처리가 불가능함. (거리 계산을 해야 하기 때문)
# 따라서 reshape을 통해 이미지를 1차원 벡터로 펼침.
# shape 출력 결과를 보면 알 수 있듯이, 8*8 이미지 -> 64 길이 벡터로 처리하여 knn이 처리 가능하도록 함
print(digits.images.shape)
data = digits.images.reshape((n_samples, -1))
print(data.shape)

Xd_tr, Xd_te, yd_tr, yd_te = train_test_split(data, digits.target, test_size=0.2, random_state=0) # train, test 데이터 분할
knn_d = KNeighborsClassifier(n_neighbors=6) # knn 알고리즘
knn_d.fit(Xd_tr, yd_tr) # 학습
yd_pred = knn_d.predict(Xd_te) # 예측
print("Digits 정확도 : ", accuracy_score(yd_te, yd_pred))

# ConfusionMatrixDisplay.from_estimator(추정치, X, y) : 추정치, 데이터, 레이블이 주어졌을 때 혼동 행렬을 그리는 함수
# 실제 레이블과 예측 레이블만이 주어졌을 땐 ConfusionMatrixDisplay.from_predictions(y_true, y_pred)
disp = ConfusionMatrixDisplay.from_estimator(knn_d, Xd_te, yd_te) # knn 예측 결과(추정치) 기반 실제 정답과 비교한 혼동 행렬을 그림
plt.title("Digits Confusion Matrix (KNN)")
plt.show()

K-Means 클러스터링

 K-Means 클러스터링은 레이블이 없는 데이터를 학습하는 비지도 학습의 가장 대표적인 알고리즘이다. 이는 주어진 n개의 관측 값을 k개의 클러스터로 분할하며, 관측 값들은 거리가 최소인 클러스터로 분류된다.

 K-Means 클러스터링 알고리즘은 초기 중심점 위치에 따라 결과가 크게 달라지고, 때로는 도메인 지식에 따라서도 결과가 달라질 수 있다. 따라서 여러 번 중심점(centroid)를 설정해 최적의 값을 찾는데, 이것의 대표적인 방법에는 Elbow method와 Silhouette analysis가 있다.

 이는 많은 데이터셋에 대해서도 클러스터링 성능이 좋다는 장점이 있다. 그러나, 클러스터 모양이 복잡하거나 크기가 다르면 제한적인 성능을 보이므로 다른 알고리즘을 고려해야 한다.

 K-means 클러스터링은 군집 중심점(centroid)라는 특정한 k개의 임의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법으로, 다음과 같은 과정에 의해 수행된다.

  1. 초기 중심점 설정
  2. 중심점을 선택된 포인트들의 평균 지점으로 이동함.
  3. 이동된 중심점에서 다시 가까운 포인트를 선택함.
  4. 다시 중심점을 평균 지점으로 이동하는 프로세스를 반복적으로 수행함.
  • 정의 : k개의 중심(centroid)를 추정하여 각 샘플을 가장 가까운 중심에 할당하고, 중심을 재계산하는 과정을 반복하여 군집 내 제곱합(SSE)를 최소화함.
  • 목표 함수
    J=∑i=1k∑xj∈Ci∥xj−μi∥2 J = \sum_{i=1}^{k} \sum_{x_j \in C_i} \| \mathbf{x}_j - \boldsymbol{\mu}_i \|^2 
  • 알고리즘 : 초기 중심 설정 → 할당 단계 (closest centroid) → 업데이트 단계 (평균 재계산) → 수렴 시 종료
    • 주의 : 초기값 민감성(기본 k-means++), 비구형/밀도 가변 데이터에서 한계 → 대안 : DBSCAN, GMM
  • kNN 알고리즘은 학습을 하지 않는 알고리즘이지만, K-Means 알고리즘은 학습을 함.
import numpy as np
from sklearn.cluster import KMeans

X_simple = np.array([
    [6,3], [11, 15], [17,12], [24,10], [20,25], [22, 30],
    [85,70], [71,81], [60, 79], [56,52], [81, 91], [80, 81]
]) # 데이터

# kMeans 알고리즘, k(중심점)=2
# 두 개의 클러스터 중심점을 반복 계산해 학습
kmeans2 = KMeans(n_clusters=2, random_state=0).fit(X_simple)
print("중심점 : \n", kmeans2.cluster_centers_) # 학습 이후 찾은 중심점 좌표 출력

# 원본 데이터 출력
plt.figure()
plt.scatter(X_simple[:, 0], X_simple[:,1]) # 원본 데이터 표시
plt.title("Raw Points for K-Means")
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

# K-Means 알고리즘 수행 후 결과
plt.figure()
# 각 데이터에 지정한 클러스터에 따라 표시
plt.scatter(X_simple[:, 0], X_simple[:,1], c = kmeans2.labels_)
# centroid 좌표 표시
plt.scatter(kmeans2.cluster_centers_[:, 0], kmeans2.cluster_centers_[:,1], marker='x', s=200) 
plt.title("K-Means Result (k=2)")
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
profile
인화
얼렁뚱땅 바보 학부생...
이전 포스트

Genetic Algorithm

0개의 댓글