Group Normalization

1. Introduction

배치 정규화(Batch Norm, BN) : (미니)배치 내에서 계산된 평균과 분산으로 특성 정규화

• 배치 통계의 확률적 불확실성은 일반화를 향상시키는 정규화로 작용하기도 함.
• 배치 차원에서 정규화하는 독특한 동작으로 인해 충분히 큰 크기의 배치가 필요(ex. 작업자당 32개 이미지)하며, 배치 크기를 줄이면 모델 오류가 증가한다는 단점이 존재함.
• 최근 많은 모델들은 메모리를 많이 소비하는 non-trivial batch size 크기로 훈련
  → BN에 대한 과한 의존 ⇒ 메모리 제한으로 인해 큰 용량의 모델 탐지 어려움
• Detection, Segmentation, Video Recognition와 같은 컴퓨터 비전 작업 → 배치 크기 제한 필요
  • (ex) Fast/er and Mask R-CNN → batch size 1 or 2 images (높은 해상도 위해)
  • 이 경우, BN을 linear layer로 변환하고, frozen함.
    → 작은 배치 사이즈로 쓰면 힘드니까 평균, 분산을 고정시키고 선형 레이어로 쓴다는 의미
    
• 3D convolution을 활용한 video classification → spatial-temporal feature가 존재해 temporal length와 batch size 사이의 trade-off 발생 → 즉, temporal length를 길게 가져가면 batch size를 줄여야 하고, batch size를 늘리면 temporal length를 짧게 가져가야 하는 상황이 발생
  
• BN의 사용은 종종 이러한 시스템이 모델 설계와 배치 크기 간의 타협을 해야 함을 요구함.

Group Normalization(GN)

• 채널을 그룹으로 나눈 다음, 각 그룹 내에서 평균과 분산을 계산해 정규화 수행
• GN의 계산은 배치 크기와 무관하며, 배치 크기의 폭 넓은 범위에서 정확도가 안정적임.
• 넓은 범위의 배치 크기에서 매우 안정적으로 동작함.

Group Normalizatioon (GN)이 왜 좋은지?

• SIFT 및 HOG와 같은 많은 고전적 feature들이 그룹 단위 특징을 지니며, 그룹 단위 정규화를 포함함.
• (ex) HOG 벡터는 여러 공간 셀의 결과로, 각 셀은 정규화된 방향 히스토그램으로 표현함.
• 마찬가지로, GN의 채널을 여러 개의 그룹으로 나누고 각 그룹 내의 feature를 정규화하는 레이어 제안
  • 이러한 GN은 배치 차원을 활용하지 않으며, 그 계산도 배치 크기와 독립적이며, 다양한 배치 크기에서도 안정적으로 동작함.
  • 배치 크기에 의존적이지 않기에 배치 크기가 변경되더라도 pre-training에서 fine-tuning으로 자연스럽게 전이될 수 있음.
  • COCO object detection, segmentation을 위한 Mask R-CNN이나 Kinetics 비디오 분류를 위한 3D 컨볼루션 네트워크에서도 더 나은 결과를 보임.
  • LN 및 IN 대신해 사용될 수 있으며, Sequential 또는 Generative 모델에도 적용할 수 있음.

배치 차원에서 정규화 하지 않는 기존의 방법

• Layer Normalization
• Instance Normalization
• 이 방법들은 Sequential models(RNN/LSTM) 또는 Generative models(GANs) 훈련에 효과적이나, visual recognition에서 제한된 성공 (→ GN이 더 나은 결과를 보임)

2. Related Work

Normalization

• 입력 데이터 정규화 → 학습 속도 빨라짐
• Local Response Normalization (LRN) : 각 픽셀에 대해 작은 이웃 영역 내에서만 통계를 계산함.
• Batch Normalization (BN) : Batch dimension을 따라 보다 Global Normalization을 수행하며, 모든 layer에 대해 이를 수행하도록 제안됨.
  • “배치(batch)”라는 개념이 항상 존재하는 것은 아니며, 경우에 따라 변경될 수 있음.
  • (ex) inference 시에는 학습 데이터에서 미리 계산된 평균과 분산이 사용되며, 주로 running average 방식을 통해 계산되고, 테스트 시엔 정규화가 수행되지 않음.
  • 타겟 데이터 분포가 변경될 경우, 미리 계산된 통계값도 변경될 수 있는데, 이로 인해 학습, 전이, 테스트 시의 일관성 문제가 발생함.
• 배치 차원을 활용하지 않는 정규화 방법들
  • Layer Normalization (LN)
    • 채널 차원(channel dimension)을 따라 정규화 수행
  • Instance Normalization (IN)
    • 각 샘플별로 Batch Normalization과 유사한 연산을 수행
  • Weight Normalization (WN)
    • feature가 아니라 filter weights를 정규화하는 방식
• 이러한 방법들은 batch dimension에서 발생하는 문제를 겪지 않지만, 여전히 많은 visual recognition 작업에서 BN의 정확도를 따라가지 못함.

.

Addressing small batches

• Batch Renormalization (BR)
  • 두 개의 추가 매개변수를 도입하여 BN의 평균과 분산 추정치를 특정 범위 내로 제한해 배치 크기가 작을 때의 변동을 줄임.
  • 작은 배치 환경에서 BN보다 더 나은 정확도를 보이나, BR도 배치에 의존적이며, 배치 크기가 줄어들 때 여전히 정확도가 저하된다는 문제 존재
• Synchronized BN (SyncBN)
  • 작은 배치를 사용하지 않으려는 방법
  • 여러 개의 GPU에서 계산된 배치 통계를 공유해 배치 크기를 키운 것처럼 동작하도록 함.
  • 이 방법은 작은 배치 문제를 해결하는 것이 아니라, 문제를 하드웨어 및 엔지니어링 요구사항으로 전가하는 것에 불과함. (이러한 이유에서 더 많은 하드웨어 자원을 필요로 함)
  • 비동기 솔버 ASGD(Asynchronous Stochastic Gradient Descent)를 사용할 수 없음.
  • 이러한 문제로 인해 Synchronized BN (SyncBN)의 활용 범위가 제한됨.
• 기존 연구들 → 배치 통계 계산 방식을 조정하는 방식이었다면 GN은 애초에 배치 통계를 계산할 필요가 없음. (배치 통계 방식을 회피)

Group-wise computation

• Group convolutions은 AlexNet에서 모델을 두 개의 GPU에 분산시키기 위해 처음 제안되었고, 이후 그룹을 모델 설계의 한 차원으로 활용하는 개념이 활발히 연구되기 시작함.
• ResNeXt : 네트워크의 depth, width, grous 간의 trade-off 조사
  • 비슷한 연산량을 유지하면서도 그룹 수를 늘리면 정확도 향상
• MobileNet 및 Xception : channel-wise convolution 활용
  • 그룹 수가 채널 수와 같은 특수한 형태의 그룹 합성곱
• ShuffleNet
  • channel shuffle 연산 제안
  • 그룹으로 나뉜 특징 맵의 축을 재배열하는 방식 도입
• 이러한 방법들은 모두 채널 차원을 그룹으로 나누어 활용하는 공통점 존재
• GN은 이러한 방법들과 관련이 있긴 하지만, group convolution을 필요로 하지 않음.

3. Group Normalization

• SIFT, HOG, GIST와 같은 고전적 feature들은 설계상 group-wise 표현 방식을 따름.
  • 즉, 특정 기준으로 그룹을 만들어 특징을 표현함.
  • 또한, 이러한 특징들은 히스토그램 기반 표현 방식을 사용함.
    • HOG : 이미지의 각 작은 영역에서 Gradient의 방향 분포를 히스토그램으로 나타냄.
    • SIFT : 이미지의 특정 키포인트 주변에서 경사도 방향 히스토그램을 계산하는 방식으로 Feature를 만듦.
    • GIST : 이미지를 여러 스케일과 방향으로 필터링한 후, 각 필터 응답을 지역적인 통계량(히스토그램)으로 요약함.
• 이러한 feature들은 각 히스토그램 또는 각 방향에 대해 group-wise normalization을 적용해 처리됨.
  • HOG : 작은 블록별 경사도 크기 정규화
  • SIFT : 키포인트 주변의 히스토그램을 정규화해 조명 변화 줄임.
• 고차원 feature 표현 방법인 VLAD 및 Fisher Vectors (FV)도 group-wise feature
  → 이 경우 그룹은 특정 클러스터와 관련된 서브 벡터로 해석 가능함.
  → 즉, 특정 클러스터(ex. k-means clustering에서 생성된 중심점)과 관련된 서브 벡터를 의미함.
  → VLAD : 각 특징점이 어떤 클러스터에 속하는지를 기반으로 특징 벡터 구성
  → Fisher Vector : GMM(Gaussian Mixture Model)을 기반으로 특징을 클러스터별로 정리한 후, 각 클러스터에 대해 통계적인 정보를 표현함.
  

정리하면, 기존 로컬 특징이든, 고차원 특징이든 그룹을 기준으로 묶어서 표현하는 방식이 많음.

• Deep Neural Network feature를 비구조적인 벡터로 생각할 필요가 없음.
  → 어떤 필터와 그 필터의 수평 반전은 유사한 필터 응답 분포를 가질 가능성이 높음.
  → 다시 말해, 어떤 방향으로 된 엣지를 감지하는 필터가 있다면, 그 필터를 좌우로 뒤집은 필터도 비슷한 역할을 할 수 있음. (유사한 필터 응답 분포를 지님)
  → 따라서 이 두 개의 필터는 서로 비슷한 특징을 가지므로 함께 정규화 가능함.
  → 이러한 자연스러운 관계를 통해 필터 그룹을 정의하고 정규화하면 성능 향상 가능
  → 더 깊은 계층에선 주파수, 모양, 질감, 조명 변화 등 다양한 기준을 사용해 그룹을 만들 수 있고, 이러한 요소들은 서로 상관관계를 가질 수 있으며, 상호 의존적인 특징을 형성함.

  CNN에서 학습된 필터들이 단순한 개별적인 벡터가 아니라, 서로 구조적으로 연관될 수 있음.

• 신경과학 연구에서도 뉴런의 반응을 정규화하는 패턴이 존재하며, 이를 딥러닝에도 적용 가능함.

 요약하면, CNN 필터들을 다양한 기준에서 살펴봤을 때, 이들은 구조적인 관계성을 지님.
 필터들이 가지는 구조적 관계성을 그룹으로 만들고, 그룹 단위 정규화 ⇒ Group Normalization

---

정리

 기존 배치 정규화는 배치 단위로 정규화해서, 배치 사이즈의 영향을 많이 받고, RNN이나 LSTM과 같은 모델에서 타임 스텝이 아닌 배치를 통해 통계를 내고 고려해서 최적이 아닌 분산과 평균으로 정규화 될 수 있다! 이런 문제점이 존재함.

 이걸 해결하기 위해 나온게 LN, IN과 같은 방법들임.

 LN은 같은 샘플, 모든 채널을 기준으로 IN은 하나 샘플, 개별 채널을 기준으로 정규화를 하니까 배치 사이즈의 영향을 받지 않고, 타임 스텝마다 정규화가 가능해서 생성형 모델이나 시퀀셜 모델에 사용하기 좋았는데, 단점은 Visual recognition task에서 그렇게 좋은 결과를 내지 못했다는 것.

 이를 해결하는 것이 GN.

 이 GN이 가능한 이유는 CNN 필터가 학습하는 특징들 간 관계가 어느 정도 연관성을 가지고 있어서 이것들을 그룹화할 수 있어서임.

 그래서 정해진 그룹별로 정규화를 수행하는 게 GN이고 Visual recognition task에서 IN, LN보다 좋은 성능을 보였고, 배치 사이즈에 독립적이라서 LSTM, RNN과 같은 IN, LN이 사용되는 것들에서도 GN을 사용하면 좋은 성능을 보일 수 있음.

 만약 그룹이 단 하나의 채널만 지닌다면, GN=IN이고, 그룹이 모든 채널을 포함하면 GN=LN이 되는 관계성을 지님.
→ 즉, GN은 IN과 LN을 일반화한 방식이라 상황에 따라 적절한 그룹 수를 조절하면 됨

---

간단 요약

** Normalization (”정규화”, “feature scaling”)

• 다양한 측도의 데이터들을 공통의 스케일로 변환하는 작업
• 데이터의 범주를 바꾸는 데이터 스케일링 관점
• Data Input을 정규화함으로써 weight, bias의 학습을 안정적이고 빠르게 할 수 있음.
• (ex) z-score normalization

** Regularization (”정규화”)

• 모델 학습에 패널티를 부여해 모델의 복잡도를 낮추는 과정
• 손실 함수에 규제항을 추가해 과적합 제어
• (ex) Regularizer(L1, L2), Dropout, Early-stopping, etc…
  

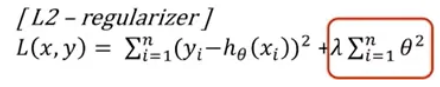
** Batch Normalization : Normalization 효과를 Batch Normalization으로 확장한 것

• 각 레이어의 Input을 Batch 단위로 Normalization
• 더 깊은 신경망에서 안정적이고 빠르게 학습
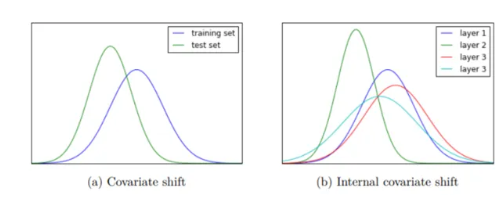
• Data의 internal covariate shift를 해소함으로써 얻을 수 있음.
• covariate shift : test input distribution이 train input distribution에서 변화해 달라지는 현상 → 모델 일반화 성능에 부정적 영향
• Internal covariate shift : Deep Neural Network 내 hidden layer의 관점에서 나타나는 Covariate shift 현상
  

** Batch Normalization의 한계

• 전체 데이터가 대상이 아닌 배치 단위 통계량 활용
  → 해결 : Group Normalization
  
• RNN 구조에선 하나의 배치가 매 time-step마다 서로 다른 통계량을 지녀 배치 대상 정규화가 매 time-step, 매 layer마다 새로 적용되어야 함.
  → 해결 : Layer Normalization, Instance Normalization
  → Layer Normalization : 각 타임 스텝에서 전체 채널 기준 정규화
  → Instance Normalization : 각 타입 스텝에서 개별 채널 기준 정규화
  → 시퀀스가 긴 경우에도 각 타임 스텝을 독립적으로 정규화하기에 RNN, LSTM 같은 구조에서도 안정적으로 작동함.

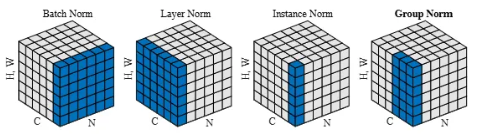
** Group Normalization

• BN은 채널을 공유하는 모든 배치가 함께 정규화되나, LN, IN, GN은 배치가 아닌 채널 단위로 묶여서 정규화됨.

** 왜 채널을 중심으로 그룹화?

• The channels of visual representations are not entirely independent.
• 예를 들어 CNN Feature Map → 다양한 특징들. 독립적으로 존재하는 것이 아니기에 함께 묶여서 분석될 수 있음.

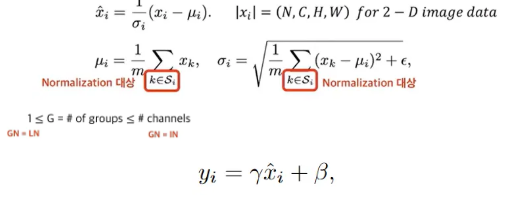
** Formulation

• 4가지 Normalization 공식은 같고, Normalization 대상만 다름.
  • $x$ = the feature computed by a layer
  • $S_i$ = the set of pixels in which the mean and std are computed
  • m = the size of set
• Batch Normalization : Pixels sharing the same channel index are normalized together (N, H, W)
• Layer Normalization : Pixels on the same sample are nomalized together (C, H, W)
  • 레이어의 모든 채널이 similar contributions를 지닌다고 가정
• Instance Normalization : Pixels on the same sample and channel are normalized together (H, W)
  • 오직 spatial dimension에만 의존하므로 채널 의존성 활용 기회를 놓침
• Group Normalization : Pixels on the same group are normalized together (group of channels * (H,W))
  • [G = C] : Group has only 1 channel (GN = IN)
  • [G = 1] : GN = LN (그룹이 모든 채널을 포함)

** Code

---