Uncertainty in deep learning

이 논문의 또다른 중요한 포인트 중 하나는 uncertainty 정보를 활용했다는 것입니다. 그래서 제목에 Probabilistic이라는 말이 들어가게 되었구요. uncertainty의 개념은 deep learning에서 처음 나온 것은 아니나, 이 논문에서도 언급하고 있는 Alex Kentall과 Yarin Gal의 논문 "What uncertainties do we need in bayesian deep learning for computer vision?"을 시작으로 deep learning기반의 컴퓨터 비전 문제에서 uncertainty의 활용에 대한 연구가 많이 이루어졌습니다. Yarin Gal의 "Uncertainty in Deep Learning"은 학위논문임에도 불구하고 엄청난 인용수를 자랑하기도 합니다.

이 글에서 uncertainty의 개념을 자세히 설명하기는 무리가 있지만, 간단히 짚고 넘어가도록 하겠습니다. uncertainty는 말 그대로 불확실성, 즉 뉴럴넷을 통해 얻을 수 있는 결과에 대해 얼마나 믿을 수 있는지를 나타냅니다. uncertainty는 크게 aleatoric uncertainty와 epistemic uncertainty로 나뉩니다. 먼저 위 논문에 나온 그림을 보여드리겠습니다.

aleatoric uncertainty는 데이터 자체에 내재된 uncertainty, 즉 sensor noise라던지, label noise 등에 의한 uncertainty를 가리킵니다. 간단히 예를 들면, image semantic segmentation 문제에서 클래스1과 클래스2의 경계에 있는 pixel들에 대해서는 label을 1,2 중 어느 쪽으로 해야할지 애매하고, label의 일관성이 다소 떨어질 수 있습니다. 그리고 이는 학습에 영향을 주게 될 것이고, 클래스 1, 2의 경계에 있는 pixel을 네트워크에 넣으면 어떤 때는 1로, 어떤 때는 2로 결과를 내게 되겠죠? 그러면 사용자는 이 결과를 믿기가 어렵게 되고, 높은 uncertainty를 갖는다고 볼 수 있습니다. 위 그림의 (d)를 보시면 물체의 경계 부분에서 높게 나타난 것을 확인할 수 있습니다. 기존의 뉴럴넷은 결과만을 냈다면, uncertainty의 개념이 포함된 뉴럴넷은 그 결과에 대한 불확실성을 함께 출력해주는 것입니다.

epistemic uncertainty는 뉴럴넷 모델이 갖고 있는 uncertainty를 말합니다. 즉, 뉴럴넷이 학습하고자 하는 데이터셋을 완벽히 모델링하지 못함에 따라 생기는 uncertainty입니다. 이는 모델의 capacity가 충분히 크고, 데이터셋이 충분히 확보되면 해결되는 uncertainty로 볼 수 있습니다. 위 그림의 (c), (e)를 함께 보시면 왼쪽 아래 보도블럭부분이 segmentation이 잘 안 되었고, epistemic uncertainty도 높게 나타난 모습을 보여줍니다. 원래 이미지를 보시면 도로와 보도 블럭이 색이 비슷해서 구분하기가 쉽지 않죠? 이를 구분할 수 있으 정도로 모델이 충분히 학습되지 않은 것으로 볼 수 있습니다. 그래서 uncertainty가 높게 나타난 것이구요. 하지만 보도블록과 도로를 구분할 수 있을 정도로 충분히 많은 데이터가 주어진다면 뉴럴넷은 더 정확하게 segmentation을 수행할 수 있고, epistemic uncertainty는 낮게 나타날 것입니다.

저도 uncertainty에 대한 이해가 아주 높지는 않고, 너무 깊게 들어가면 삼천포로 빠질 것 같아 여기까지만 정리하도록 하겠습니다. LaserNet에서는 데이터의 uncertainty를 나타내는 aleatoric uncertainty를 활용하는데 초점을 맞추었습니다. 쉬운 예를 들자면, 멀리 있는 차는 LiDAR 데이터가 듬성듬성 찍힐 것이고, 그런 LiDAR point들로부터 추정한 bounding box는 많은 point로부터 얻은 bounding box에 비해 신뢰도가 떨어지겠죠? 그런 것들을 잘 반영할 수 있도록 설계하였다고 보시면 되겠습니다. 자세한 내용은 이후 설명에서 이어가도록 하겠습니다.

Gaussian mixture model based modeling

지난 글에서 설명드렸듯이 LaserNet은 Range Image grid의 각 point에 대해

• class probability (Car, Pedestrian, Cyclist) 예측
• 각 클래스마다 bounding box parameter 예측
  - relative center $(d_x, d_y)$
  - relative orientation $(w_x, w_y) = (\cos w, \sin w)$
  - dimensions of the box $(l, w)$
  

을 수행합니다. 여기서 짚고 넘어가야할 부분이 있습니다. class 확률은 우리가 흔히 아는 sigmoid 기반의 확률을 출력하지만, bounding box parameter의 경우 직접적으로 값을 예측하는 것이 아닌, 값의 분포를 예측한다고 말씀드리면서 글을 마무리지었습니다. bounding box parameter가 갖는 분포를 Gaussian Mixture Model(이하 GMM)로 가정하고, 네트워크가 GMM의 parameter, 즉 $k$(몇 개의 Gaussian 분포의 결합으로 모델링할 것인지를 나타내는 GMM의 hyperparameter)개의 mean($\mu_k$), standard deviation($s_k$), mixture weight($\alpha_k$)를 출력하도록 하는 것입니다.

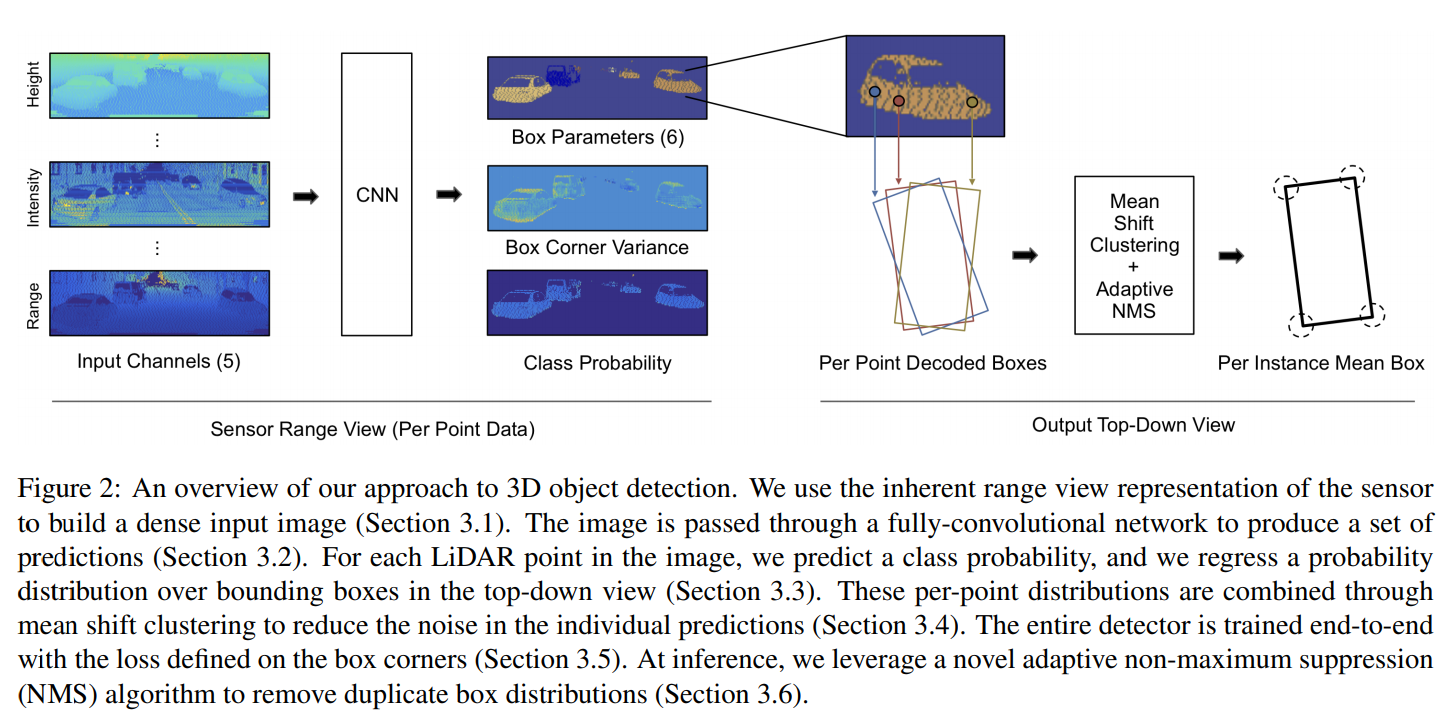
LaserNet 전체 구조 그림을 다시 한 번 가져와 봤습니다.
먼저, 네트워크가 최종적으로 출력해야하는 것을 다시 한 번 정리해보겠습니다. 예측해야 하는 6개의 parameter는 relative center 2개, relative orientation 2개, dimensions of the box 2개이고, 각각에 대해 $k$개의 mean과 standard deviation을 출력해야 합니다. 그런데 standard deviation은 6개의 parameter에 대해 공통된 하나의 값을 사용한다고 합니다. 즉 mean은 6개(위 그림의 Box Parameters)를, standard deviation(위 그림의 Box Corner Variance)은 1개를 출력하게 되는 것이고, 이 7개의 parameter를 $k$ 묶음 출력하는 것입니다. 즉 range image의 각 point에 대한 출력은, 각 class마다

• class probability $1$개
• 각 bounding box parameter의 mean $6k$개
• bounding box parameter들의 공통 standard deviation $k$개

가 되고, 네트워크 구조 그림에서 확인할 수 있습니다. 만약 class 종류가 $C$개라면 네트워크 출력의 총 개수는 $C\times(7k+1)$개가 되겠네요. 보다 정확히 하면, class마다 $k$를 다르게 설정할 수 있기 때문에, $\Sigma_{c=1}^C(7k_c+1)$개가 됩니다. 실제로 논문의 실험파트를 보면 Car class에 대해서만 $k=3$으로 정하고, pedestrian, cyclist class에 대해서는 $k=1$로 설정하여 unimodal distribution을 학습하도록 했습니다.

여기서 $k$는 object detection에서의 anchor의 개념과 유사하다고 생각할 수 있습니다. $k$개의 distribution 각각은 조금씩 다른 방식으로 bounding box prediciton을 수행하게 되고, 네트워크가 예측한 mixture weight는 이 $k$개의 prediction 중 어느 것이 가장 믿을만한지를 나타내게 됩니다.
우리가 잘 알고 있는 anchor의 개념으로 생각해보면 형태와 크기 다양한 Car class는 3개의 anchor, 비교적 다양성이 적은 Pedestrian과 Cyclist는 하나의 anchor를 사용했다고 볼 수 있겠습니다.

논문에서 class probability를 예측할 때 (1) class 각각에 대한 branch를 분리해서 만든 후 sigmoid로 확률을 예측하는지, (2) softmax로 모든 class에 대한 확률을 출력하는지 명확하지 않지만, 섹션 3.6에서 threshold로 $1/C$를 사용한다는 내용으로부터 sigmoid를 사용했을 것이라고 추측할 수 있습니다. softmax를 사용하면 3가지 class 확률값의 합은 1이므로 적어도 하나의 확률값은 $1/C$이상의 값을 갖게 됩니다. 하지만 어떤 point는 어떤 class에도 속하지 않는 background일 수 있습니다. 따라서 softmax는 적절하지 않습니다. 반면, 각 point에 대해 Car일 확률, Pedstrian일 확률, Cylist일 확률을 각각 sigmoid로 출력하면 각 확률을 threshold $1/C$와 비교해서 모두 $1/C$보다 작으면 background point로 생각할 수 있게 됩니다. 사소한 부분이지만 논문에 언급되어 있지 않은 부분이라 제 생각을 정리해두었습니다.

Mean shift clustering

이렇게 우리는 range image의 각 point에 대해 bounding box parameter의 distribution을 얻을 수 있게 되었습니다. 네트워크가 잘 학습되었다면, 같은 object에 속한 point의 네트워크 출력으로 얻은 distribution은 비슷해야 할 것입니다. 즉 한 물체에 속한 point들은 비슷한 bounding box를 예측해야한다는 것이죠. 그러면 우리는 하나의 object에 대해 여러 개의 (비슷한) bounding box prediction들을 갖게 됩니다. 이 여러 개의 bounding box prediction을 모두 사용할 수는 없으니, 하나를 고르든, 결과들을 잘 융합하든 해야겠죠? 이 논문에서는 prediction 결과로 얻은 bounding box center들을 mean shift clustering을 통해 융합하여 정확한 bounding box center를 찾고자 했습니다. 그리고 mean shift clustering은 각 class(Car, Pedestrian, Cyclist)에 대해, 그리고 각 class에 대응되는 GMM의 $k$개 distribution 각각에 대해 수행하게 됩니다. mean shift clustering에 대해 간단히 설명드리면, 각 point에서 시작하여 point의 밀도가 높은 곳으로 계속 이동하다보면 밀도가 가장 높은 지점을 중심으로 뭉치게 되는 것을 이용한 clustering 방법입니다. mean shift clustering으로 검색을 해보시면 좋은 자료들이 있으니 참고해보시면 좋을 듯 합니다. LaserNet에서는 BEV(Bird-Eye-View) map을 ${\Delta}x, {\Delta}y$의 크기(논문에서는 각각 0.5m 사용)를 갖는 bin으로 쪼갠 BEV grid map 상에서 사용할 수 있는 mean shift clustering의 fast approximation을 제안했습니다.

1. 먼저 1개 이상의 box center를 포함하는 bin에 대해, box center의 mean을 계산해 해당 bin에 initial mean $m_i$를 할당합니다. 그리고 해당 bin에 속한 center를 prediction한 range image의 point들의 집합 $S_i$를 해당 bin에 $m_i$와 함께 할당합니다.
2. 다음의 수식으로 $m_i$를 update합니다.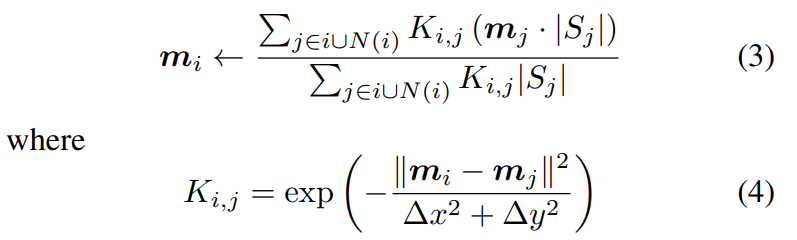여기서 $i$는 mean shift clustering을 수행하는 $i$th bin을 나타내고, $N(i)$는 $i$ bin의 8개의 neighbor bin에 해당합니다. 즉 $i$th bin을 중심으로 한 9개의 bin에 속한 mean들의 mean을 계산하여 update하는 것입니다.

   수식(3)을 잘 보시면 $m_j$에 곱해지는 weight는 $K_{i,j}|S_j|$로 생각할 수 있습니다.
   $|S_j|$는 해당 bin에 속하는 center를 예측한 point의 개수이므로, 더 많은 point가 object의 center라고 예측한 bin에 가중치를 두겠다는 것으로 이해할 수 있습니다.
   $K_{i,j}$는 수식(4)로 정의되는데요, exp 안의 분자를 보면 $i, j$th bin의 mean $m_i, m_j$ 사이의 차이의 제곱이므로, $i$th bin의 mean $m_i$과 비슷한 mean을 갖는 bin에 큰 가중치를 할당하는 것으로 이해할 수 있습니다(분모는 normalization 정도로 생각할 수 있습니다).

3. update한 $i$th bin의 mean이 $j$th bin에 속하게 되었다면, 다음 수식으로 $i$th bin을 $j$th bin에 merge합니다.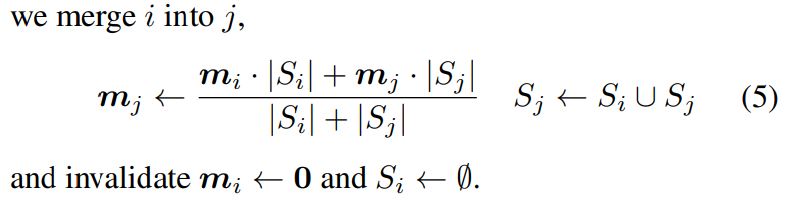즉 각 bin에 속한 point 개수를 가중치로 하여 두 bin의 mean을 결합하여 $j$th bin에 할당하고, $j$th bin에 속한 point $S_j$는 $i$th bin에 속한 point의 집합 $S_i$를 포함하게 되고, $i$th bin에 할당되었던 mean $m_i$, point 집합 $S_i$는 제거합니다.

위 3단계의 과정을 정해진 횟수(논문에서는 3회)만큼 반복하여 mean shift clustering을 수행하게 됩니다. 이러한 grid 기반의 fast approximation이 GPU 연산에 보다 적합하여 효율적인 연산이 가능하다고 주장하고 있습니다. mean shift clustering의 결과로 생긴 각 cluster에 대해 같은 cluster가 갖는 bounding box distribution을 정의해야 하겠습니다. 우리가 clustering을 통해 하고자했던 것은, 같은 object에 속한 point들의 bounding box distribution을 잘 융합하는 것이었으니까요. cluster의 bounding box distribution은 cluster에 속한 각 point가 예측한 bounding box distribution의 곱으로 모델링하고(각 point가 예측한 box distribution이 독립이라고 가정), 이에 따른 cluster의 bounding box distribution의 mean, variance는 다음과 같습니다. (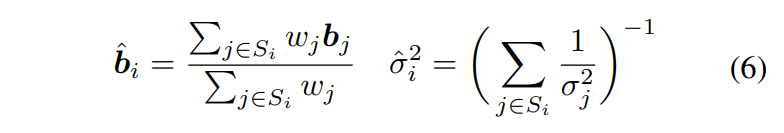$w=1/{\sigma}^2$) 왜 이렇게 되는지는 독립인 두 Gaussian PDF의 곱을 참고하시면 쉽게 이해할 수 있습니다. 그리고 각 cluster에 속한 point들로부터 예측된 bounding box와 variance들은 위 수식을 통해 계산된 cluster의 bounding box와 variance로 대체됩니다.

다시 한 번 짚고 넘어가야할 것은, 각 class에 대해, 각 point가 예측한 GMM을 구성하는 $k$개의 distribution에 각각에 대해 mean shift clustering을 수행한다는 점입니다. 즉 모든 mean shift clustering을 수행하고 나면, 각 point는
(1) 예측한 class probability
(2) point가 갖는 $k$개의 bounding box distribution 각각에 대해 point가 속한 cluster의 mean, variance로 대체된 $k$ 묶음의 bounding box parameter(point는 $k$ 묶음의 bounding box parameter를 예측하고, 같은 point라도 $k$개 중 어떤 distribution인지에 따라 다른 cluster에 속할 수 있음을 이해하는 것이 중요합니다!)
를 갖게 됩니다.

Loss functions

이제 어떻게 네트워크가 위 parameter들을 출력할 수 있도록 loss를 설계했는지 살펴봅시다.
가장 간단한 것부터 보면, range image에 속한 각 point의 class probability는 class imbalance(대부분의 자율주행 dataset이 Car class가 압도적으로 많습니다) 문제를 어느 정도 해결해줄 수 있도록 변형된 cross entropy loss인 focal loss($L_{prob,i}$)를 사용했습니다. 아래 수식이 range image 전체의 classification loss가 되고, $P$는 range image의 전체 point 개수입니다.
보편적인 3D object detector에서 bounding box parameter를 출력하는 layer는 L1 또는 L2 loss를 이용한 regression loss로 학습을 시킵니다. LaserNet의 mean($\mu_k$)을 출력하는 layer도 동일하게 학습시킵니다. 즉 그냥 regression과 동일하게 학습시키되, 모델링한 분포의 mean($\mu_k$)이라는 의미를 부여한 것이라고 보시면 됩니다. 그런데 우리는 6개의 mean뿐만 아니라, 1개의 공통 standard deviation도 예측해야 합니다. 이를 위해 서두에 언급했던 Alex Kentall과 Yarin Gal의 논문 "What uncertainties do we need in bayesian deep learning for computer vision?"에서 uncertainty를 출력하기 위해 설계한 loss를 사용합니다. 수식은 아래와 같습니다. 여기서 $b_n$은 4개의 bounding box corner를 가리킵니다. 논문의 수식 (2)를 참고해주세요.
여기서 $k^*$는, $k$ 묶음의 parameter distribution(이 때 parameter distribution은 mean shift clustering에 의해 point가 속한 cluster의 parameter distribution으로 대체된 것이겠죠!!) 중 ground truth와 가장 가까운 distribution에 해당하는 index입니다. 다음과 같이 계산합니다.
즉, GMM을 구성하는 $k$개의 Gaussian distribution 중 가장 잘 맞는 distribution을 선택한 뒤 ground truth parameter와 loss를 계산하여 학습하는 것입니다. 수식 (9)와 같은 loss로 어떻게 standard deviation이 학습될 수 있는지 궁금하신 분은 "What uncertainties do we need in bayesian deep learning for computer vision?"를 참고해주세요.

그래도 간단히 설명을 드리자면, 수식 (9)는 기본적으로 L1 loss의 형태를 갖고 있고, 분모에 standard deviation(=uncertainty)에 해당하는 $\sigma_k$가 들어가고, 뒤에 일종의 $\sigma_k$에 대한 regularization term으로 작용하는 $\log{\sigma_k}$ 가 들어가 있는 형태입니다.
${\sigma_k}$ 부분은 잠깐 없다고 생각하고, 잠시 L1 loss만 생각해봅시다.bounding box parameter의 mean을 출력하는 네트워크는 L1 loss를 최소화하도록 학습이 될 것입니다. L1 loss로 잘 학습되었다고 하더라도, L1 loss가 비교적 큰 point가 존재하겠죠? 그런 point는 ground truth box를 예측하기에 정보가 충분하지 않은 point라고 할 수 있고, 큰 uncertainty를 갖는다고 말할 수 있습니다.
다시 한 번 수식 (9)로 돌아와서, 전체 loss를 최소화하려면 L1 loss가 큰 곳에서 $\sigma_k$가 커져야 함을 알 수 있습니다. 위에서 L1 loss가 비교적 큰 point의 출력은 uncertainty가 크다고 말할 수 있다고 말씀드렸습니다. 즉 수식 (9)와 같은 loss로 학습된 ${\sigma_k}$는 uncertainty를 나타낸다고 생각할 수 있다는 것입니다. 하지만 $\sigma_k$가 무한히 커져서 전체 loss를 0으로 만들도록 학습될 수 있겠죠? 이를 막아주는 게 $\log{\sigma_k}$입니다. 이렇게 ${\sigma_k}$는 수식 (9)와 같은 loss를 통해 uncertainty를 모델링하도록 학습되는 것입니다. 제 설명만 읽으시고 이해가 되셨다면 다행이지만, 아니시라면 본 논문을 참조해주세요.

그리고 마지막으로 학습해야할 것은 mixture weight $w_k$입니다. mixture weight의 ground truth는 수식 (8)로 얻어진 $k^*$에 해당하는 distribution의 mixture weight에 1을, 그 외의 mixture weight에는 0을 label로 주어 cross entropy loss를 이용해 학습하게 됩니다. 참고로 이렇게 $k$개 distribution 중 가장 잘 맞는 distribution에 대해서만 loss를 계산하는 아이디어는 Multiple Choice Learning 논문에서 가져왔다고 합니다.

각 point에 대한 regression loss는 수식 (9)의 loss($L_{box,i}$)와 mixture weight에 대한 cross entropy loss($L_{mix,i}$)로 구성되고, 각 object에 대한 regression loss는 object에 속한 point들의 regression loss의 합으로 정의되어 아래 수식의 $\Sigma$안의 수식 형태를 갖게 되고, $n_i$은 $n$th object에 속한 point의 개수입니다. 그리고 range image 전체에 대한 loss는 최종적으로 아래와 같이 정의되며, $N$은 range image 안에 있는 object의 총 개수입니다.
최종적으로 classification loss(수식 (7))와 regression loss(수식 (10))를 합해, range image에 대한 전체 loss를 얻게 됩니다($L_{total}=L_{cls}+L_{reg}$). 이렇게 복잡한 loss에 대한 설명이 끝났습니다.

Adaptive Non-Maximum Suppression

이제 inference 단계에서 필요한 post-processing인 Non-Maximum Suppression(이하 NMS)에 관한 내용으로 네트워크에 대한 내용이 마무리가 됩니다. 일반적인 NMS는 다음의 과정으로 수행됩니다.
1. Intersection over Union(이하 IoU)가 fixed threshold보다 큰 box들을 찾는다.
2. 겹치는 box들 중 class probability가 가장 높은 것만 남기고 나머지 box들을 제거한다.

하지만 저자들은 일반적인 NMS는 다음의 2가지 이유로 LaserNet에 부적합하다고 말합니다.
1. NMS는 LaserNet이 예측하는 bounding box의 variance를 고려하지 않는다.
2. class probability가 bounding box의 quality에 대응되지 않는다.

그래서 LaserNet에서는 Adaptive NMS라는 변형된 NMS 방법을 제안합니다. fixed IoU threshold가 아닌, 예측한 variance를 이용해서 IoU threshold를 정의하고, box의 score는 class probability 대신 GMM에서 해당 bbox distribution의 likelihood(${\alpha_k}/2{\pi}\hat{\sigma_k}$)로 대체하였습니다.

논문에서는 likelihood를 ${\alpha_k}/2\hat{\sigma_k}$로 쓰고 있는데요, 아무리 생각해도 분모에 $\pi$가 빠진 듯 합니다. bounding box corner가 2차원 좌표 형태를 가지므로 two variable GMM을 생각해보면, $k$th distribution에서 mean 값의 likelihood는 ${\alpha_k}/2{\pi}\hat{\sigma_k}$가 되는 듯 한데, 혹시 제가 틀린 부분이 있다면 댓글로 지적부탁드립니다.

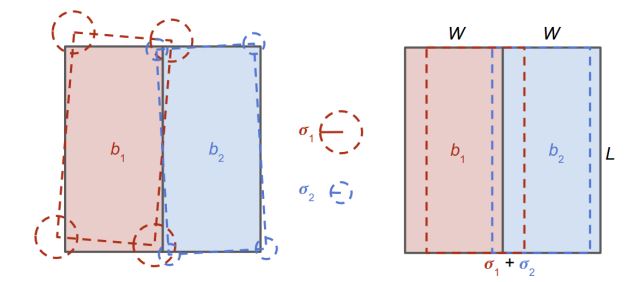
잠깐 샜는데요, Adaptive NMS 얘기로 돌아오겠습니다. top view(BEV)에서 봤을 때 ground truth bounding box들은 겹치지 않습니다. 하지만 네트워크가 예측한 box distribution은 uncertainty를 가지므로, 다른 object의 box를 예측한 것이라도 아래 왼쪽 그림의 점선과 같이 overlap이 발생할 수 있습니다.따라서 각 box distribution이 갖는 uncertainty, 즉 standard deviation을 이용해 서로 다른 box이더라도 어느 정도까지 겹칠 수 있는지를 계산할 수 있습니다. 위 그림의 오른쪽의 경우가 최악의 경우, 즉 서로 다른 박스에 대한 prediction임에도 불구하고 box가 갖는 uncertainty에 의해 최대로 겹칠 수 있는 상황입니다. 이 때의 IoU를 계산하면, 아래 수식에서 $\sigma_1+\sigma_2<w$일 경우의 IoU threshold가 됩니다.여기서 $w$는 해당 class object의 bounding box width의 평균값입니다.

otherwise, 즉 $\sigma_1+\sigma_2 {\geq} w$인 경우 IoU thereshold를 1로 한다고 되어있는데요, IoU 자체가 가질 수 있는 값의 최대가 1인 것을 생각해보면 그냥 NMS를 수행하지 않겠다는 것과 같은 말입니다. 즉 uncertainty가 너무 큰 box에 대해서는 NMS를 수행하기 애매하다는 것이겠죠.

이렇게 uncertainty를 고려하여 adaptive하게 threshold를 정하게 되고, threshold 이상의 IoU 이상의 overlap을 가질 경우 낮은 likelihood를 갖는 box를 처리하는 방법에 따라 Hard NMS, Soft NMS로 다시 나뉘게 됩니다.
Hard NMS는 가장 직관적인 방법으로, threshold 이상으로 겹친 box 중 낮은 likelihood를 갖는 box를 제거하는 방법입니다.
Soft NMS는 likelihood가 낮은 box를 제거하는 대신, likelihood가 낮은 box distribution의 standard deviation이 정확하지 않다고 가정하고, standard deviation을 증가시킵니다. 그러면 IoU threshold가 커지게 되고, 두 box 사이의 IoU는 threshold보다 작아지게 될 것입니다. 대신 likelihood가 낮은 box의 likelihood는 더 작아지게 됩니다(${\alpha_k}/2{\pi}\hat{\sigma_k}$에서 $\hat{\sigma_k}$를 더 크게 한 것이므로). 정리하면 Soft NMS는 IoU threshold 이상의 overlap이 발생했을 때 likelihood가 낮은 box를 제거하지 않는 대신, 더 큰 uncertainty를 할당하여 box score를 낮추는 것입니다.

드디어 이렇게 네트워크에 관한 부분의 정리가 끝났습니다. 이제 실험 파트로 넘어가겠습니다.

Experiments

실험파트는 논문의 table과 figure를 중심으로 빠르게 정리해보겠습니다.

LaserNet에서는 KITTI dataset 뿐 아니라, Uber에서 나온 논문인만큼 자체 제작한(?) ATG4D dataset을 실험에 사용했습니다. 공개되지 않은 데이터셋이고, KITTI보다 훨씬 큰 데이터셋이라고 합니다. table 1에서는 ATG4D에 대한 BEV detection 성능을 보여주는데요, 당시의 SOTA LiDAR only detector들보다 모든 거리 영역에서 좋은 성능을 보여주고 있음을 알 수 있고, RGB+LIDAR detector인 ContFuse에 대해서는 먼 거리에서의 vehicle, bike class에 대해 성능이 조금 떨어지는 것을 제외하고는 더 좋은 성능을 보여줍니다.
table 2는 ablation study입니다.

1. distribution prediction 형태: Mean-only(분포 예측X), unimodal($k=1$), multimodal($k\geq2$)
2. image spacing: range image의 column을 채울 때,
   Uniform: point의 elevation angle을 64개로 uniform하게 쪼개서 column을 채울 것인지,
   Laser: 실제 LiDAR의 64개 laser id를 이용해 column을 채울 것인지
3. Mean shift clustering
4. IoU threshold : fixed or Adaptive IoU threshold
5. NMS Type : Hard NMS or Soft NMS

위 5가지 항목에 대해 수행하였고, 결과에 대한 자세한 해석은 논문을 참고해주세요.
table 3는 runtime에 대한 분석입니다. range image의 장점이 가장 크게 드러나는 부분입니다. voxel이나 point 기반의 detector는 point cloud의 sparsity에서 오는 비효율성에서 벗어나기 힘든 반면, LaserNet은 dense한 형태인 range image에 대해 2D CNN 기반의 네트워크를 적용하므로 훨씬 빠른 속도를 나타내게 됩니다.table 4는 KITTI에 대한 BEV detection 성능인데요, 다른 detector에 비해 성능이 떨어지는 모습을 보여줍니다. 이에 대해 저자들은 작은 데이터셋(KITTI)으로 bounding box의 probability distribution을 학습하는 것이 어렵기 때문이라고 주장합니다. 데이터셋의 크기를 충분히 키우면(ATG4D) LaserNet이 probability distribution을 학습할 수 있게 되면서 다른 detector들보다 좋은 성능을 보이게 된다는 것이죠. 이러한 주장과 함께 다음 plot을 제시합니다.figure 6는 실제 dataset의 bounding box가 갖는 분포와 네트워크가 train set과 validation set에 대해 출력한 bounding box prediction의 분포를 비교한 것입니다. 이 figure를 정확히 이해하는 것은 쉽지 않지만, 통해 말하고자 하는 것은 KITTI와 같이 작은 데이터셋으로 학습을 시키면, 데이터셋의 bounding box distribution을 잘 학습하지 못 하고(점선과 파란색, 주황색 곡선 사이의 갭이 큼), ATG4D와 같이 충분히 큰 데이터셋으로 학습하면 bounding box distribution을 잘 학습할 수 있었다는 것(점선과 파란색, 주황색 곡선 사이의 갭이 작음)입니다.

figure 6에 대한 부연설명입니다. 위 설명을 이해하셨다면 논문을 이해하는 데 전혀 지장이 없지만 저 figure 자체를 이해하고 싶은 분들을 위해 간단한 설명을 덧붙입니다.
실제 dataset에 존재하는 ground truth bounding box paramter들의 히스토그램을 그려보면 어떻게 될까요? 아마 Gaussian distribution의 형태에 가까운 분포를 가질 것입니다. 따라서 먼저 dataset에 속한 ground truth bounding box paramter들의 mean, variance를 구해서 Gaussian distribution으로 모델링합니다. 그리고 학습된 네트워크가 train set과 validation set에 대해 출력한 bounding box들의 mean, variance를 구해서 Gaussian distribution으로 모델링을 합니다.
ground truth bounding box가 갖는 Gaussian distribution의 CDF를 기준으로 해서(figure 상에 기울기 1인 점선) train set, validation set에 대한 네트워크 출력의 Gaussian distribution의 CDF를 나타낸 것이 위 figure입니다. 이 figure를 정확히 이해하기 위해서는 통계학에서 말하는 Calibration의 개념에 대한 이해가 필요합니다. 이 글을 참고해보시는 것을 추천드립니다.

---

이렇게 길고 길었던 LaserNet의 정리를 마칩니다. range image 기반의 detector를 소개하고자 선정한 논문이었는데, range image 외에 정리해야할 요소가 너무 많아서 정말 힘들었던 논문이었습니다. 그래도 정리하면서 잘못 이해하고 있었던 부분을 발견하기도 했고, 이해가 깊어진 것 같아 뿌듯하네요.

질문, 지적은 언제나 환영입니다.
읽어주셔서 감사드립니다.