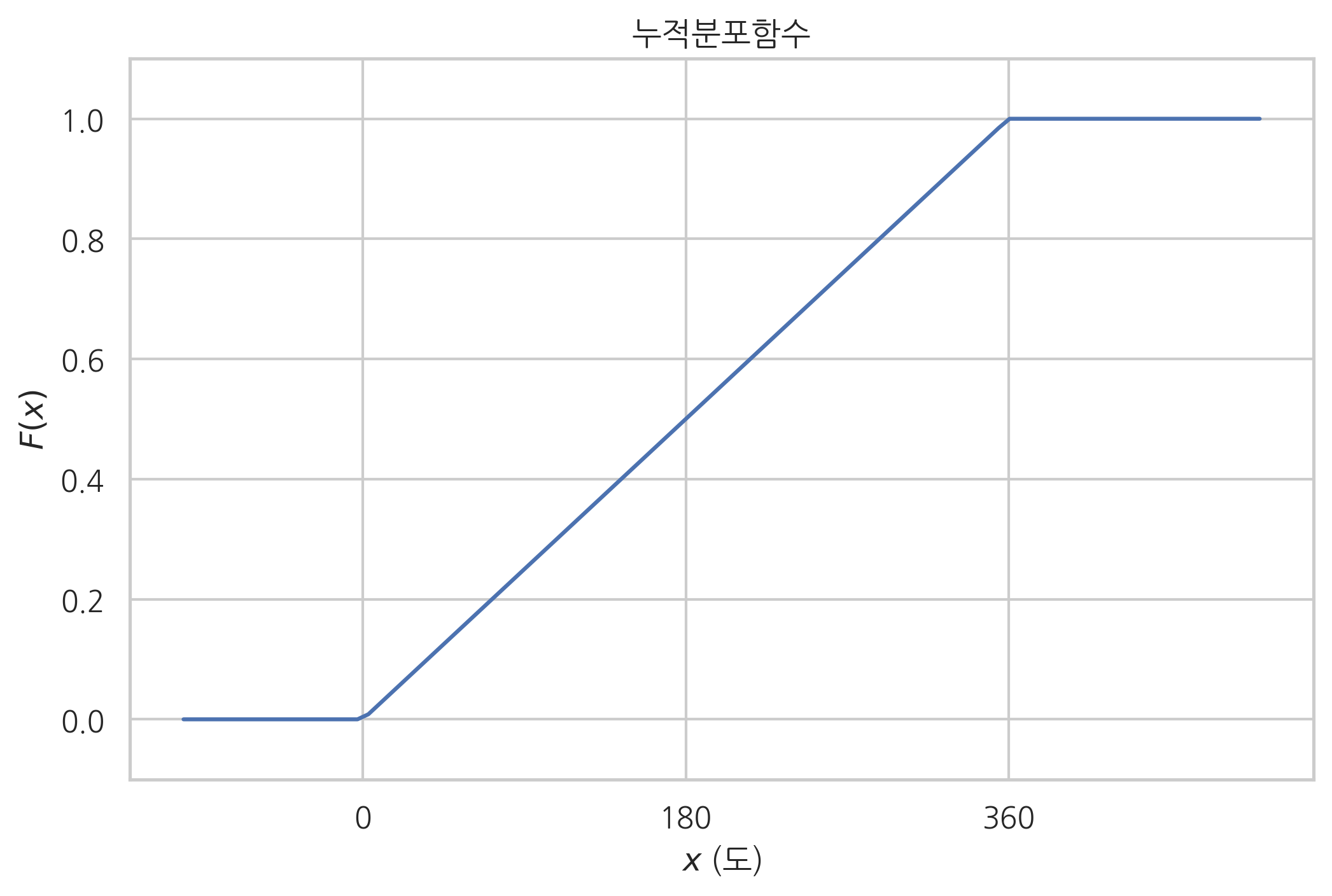
누적분포함수와 확률 밀도 함수

황민규·2023년 6월 29일

통계/수학

목록 보기

4/8

기존의 사건을 표현하기 위해서는

$a \leq X \leq b$ 와 같은 방식으로 두개의 숫자가 반드시 필요했습니다.
하나의 숫자로 interval을 정의하는 방법에 대해 고민하다 나온것이 시작점을 전부
- $\infty$ 음의 무한대로 고정하는 것입니다.

음의 무한대에서 시작되는 구간을 $Sx (x는 구간의 끝)$ 라고 말하고 해당 특수 구간에서의
확률 분포를 묘사하는 함수를 누적분포함수(cumulative distribution function) 라고 합니다.

Notation = $F(x)$ 등으로 표현한다.

$F(x) = P(Sx) = P(X\leq x)$

이 세가지 특성에 의해 누적분포 함수는 0에서 1로 단조적으로 증가하는 특성을 갖는다

단조 증가 성질에 의해 절대로 내려가지 않는다

1차원 함수를 통해 확률분포를 간결하고 정확하게 묘사하도록 해주었다.

누적 분포함수의 경우 $(-\infty, x)$ 이기에 함수를 봤을때 직관적으로 이해하기 힘들다.

즉 어떤 확률변수가 더 자주 나오는지 알 수 없다는 의미와 같다.

이를 알기위해서 구간 범위 $(-\infty, \infty)$ 를 아주 작은 숫자 $dx$ 를 가지는 구간으로 나누고 각구간의 확률을 보는것이 편하다.

$x1$ 근처에서 폭 $dx$ 를 가지는 구간의 확률을 구하면 다음 식으로 말할 수 있다.

P(x_{1} \leq X \leq x_{1} + d_{x}) = F(x_{1} + d_{x}) - F(x)

dx를 아주 작은 숫자로 줄였을 때 ( dx =0 이면 확률은 당연히 0이다)
단위 구간에서의 x1, x2를 비교해야한다 .

단위 구간 길이당 확률 값을 구하면

\frac{P(x_{1} \leq X \leq x_{1} + d_{x})}{d_{x}}

이 된다.

여기서 $d_{x}$ 를 미세하게 줄인다면,

\lim_{d_{x} \rightarrow 0}\frac{P(x_{1} \leq X \leq x_{1} + d_{x})}{d_{x}} = \lim_{d_{x} \rightarrow 0}\frac{F(x_{1} + d_{x})-F(x_{1})}{d_{x}}

다음처럼 누적분포함수의 기울기가 된다.

즉 결론적으로 누적분포함수의 미분을 통해 얻은 도함수가 확률밀도 함수가 된다.

P(x) = \frac{dF(x)}{dx}

확률 밀도 함수에서 그자체는 다름 값과의 비교지 확률이 아니다!!

다시 변환하면 $x_{1}$ 에서 $x_{2}$ 사이의 확률 밀도함수의 면적은 누적분포함수의 값만으로 계산이 가능하다.

F(x_{2}) - F(x_{1}) = \int_{x_{1}}^{x_{2}} p(u)d_{u}

처럼 표현이 가능하다.

결론적으로 누적분포함수와 확률밀도함수를 수식으로 나타내면

F(x) = \int_{-\infty}^{x} p(u)d_{u}

특징 1. 누적분포함수가 단조 증가함수이기에 확률밀도함수는 항상 0보다 크거나 같다.

특징 2. - $\infty$ , $\infty$ 를 구간으로 가지면 표본공간과 같아 확률밀도함수는 1이 된다.

해당 글을 참고하여 작성하였습니다. !

자반이랑 행복하게 살기