1. 손실 함수와 정규화: 좋은 모델이란 무엇인가?
- 지난 시간 복습:
- 이미지 분류: 컴퓨터에게 이미지를 보여주고 미리 정해진 레이블 중 하나를 맞추게 하는 작업입니다.
- 선형 분류기: 이미지 픽셀(x)에 가중치(W)를 곱해 각 클래스에 대한 점수(score)를 계산하는 간단한 모델입니다.
f(x, W) = Wx
- 손실 함수 (Loss Function) ⚖️:
- 모델이 얼마나 '나쁜지'를 알려주는 지표입니다. 즉, 모델의 예측이 실제 정답과 얼마나 다른지를 숫자로 나타냅니다.
- 우리의 목표는 이 손실 값을 최소화하는 가중치 W를 찾는 것입니다.
- 손실 함수의 두 가지 요소:
- 데이터 손실 (Data Loss): 모델이 학습 데이터에 대해 얼마나 잘 예측하는지를 측정합니다. (예: 소프트맥스, SVM 손실)
- 정규화 (Regularization): 모델의 복잡도에 대한 '벌점(penalty)'입니다. 모델이 학습 데이터에만 너무 치중하는 과적합(Overfitting)을 방지하고, 처음 보는 데이터에 대해서도 좋은 성능을 내도록 도와줍니다.
- 정규화의 원리:
- 오컴의 면도날(Ockham's Razor) 원리처럼, 여러 모델 중 더 단순한 모델을 선호하는 것입니다.
- 모델의 가중치(W)가 너무 커지지 않도록 억제하여, 모든 입력 특징에 좀 더 고르게 주의를 기울이도록 만듭니다.
- 대표적인 예시:
- L2 정규화: 모든 가중치를 제곱하여 더한 값입니다. 가중치를 전반적으로 작고 부드럽게 만듭니다.
- L1 정규화: 모든 가중치의 절댓값을 더한 값입니다. 중요하지 않은 가중치를 0으로 만들어 모델을 희소(sparse)하게 만듭니다.



2. 최적화: 최고의 가중치(W)를 찾는 여정
- 최적화(Optimization)란?
- 손실 함수라는 거대한 '산'에서 가장 낮은 지점(최소값)을 찾아가는 과정입니다. 이 지점의 W가 바로 우리가 원하는 최적의 가중치입니다.
- 손실 지형(Loss Landscape): 가중치(W) 값에 따른 손실 함수의 변화를 시각적으로 표현한 것입니다.
- 최적화 전략:
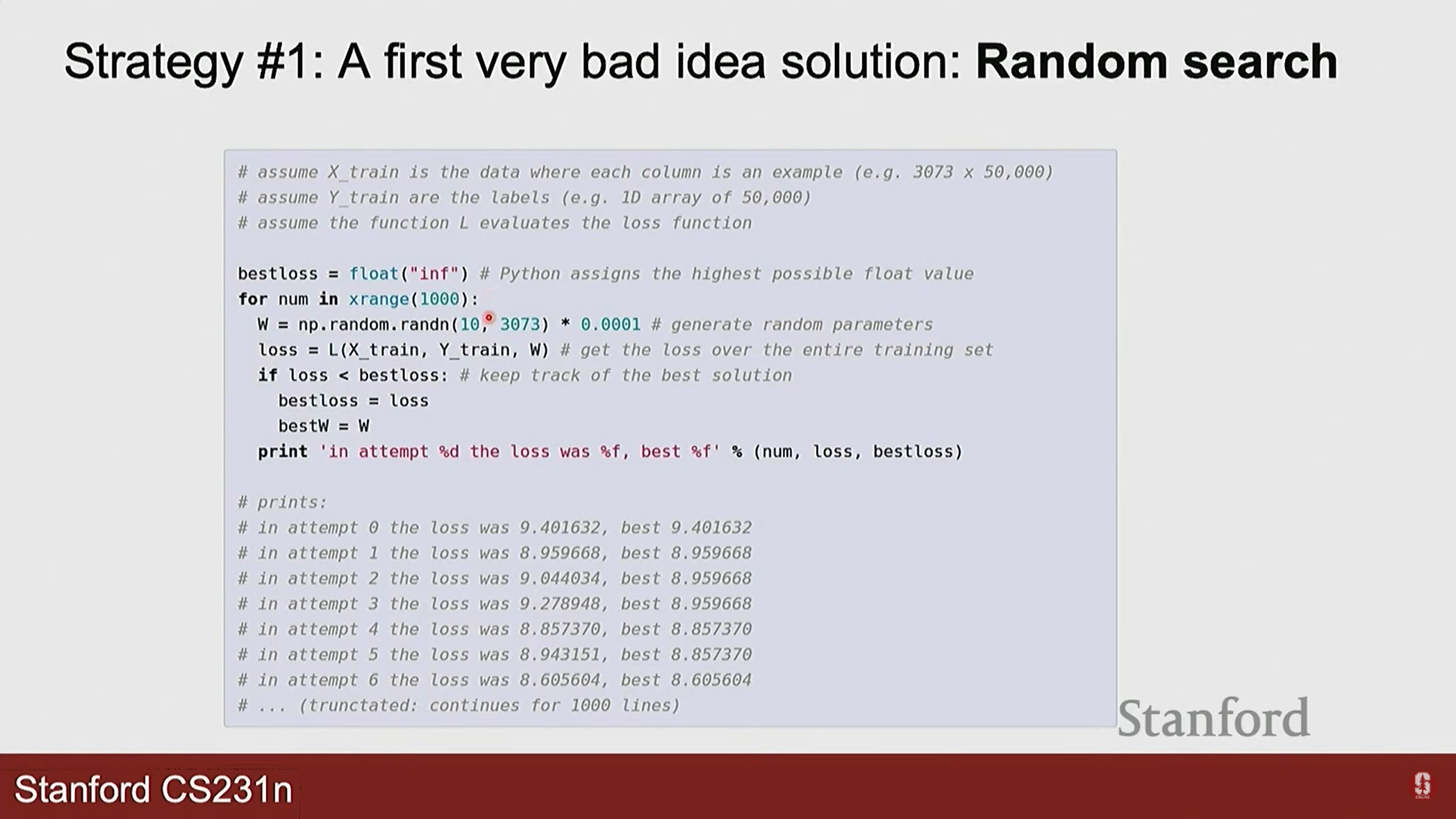
- 무작위 탐색: 가장 나쁜 방법입니다. 그냥 무작위로 W를 여러 번 시도해보고 가장 좋은 것을 고르는 방식입니다.
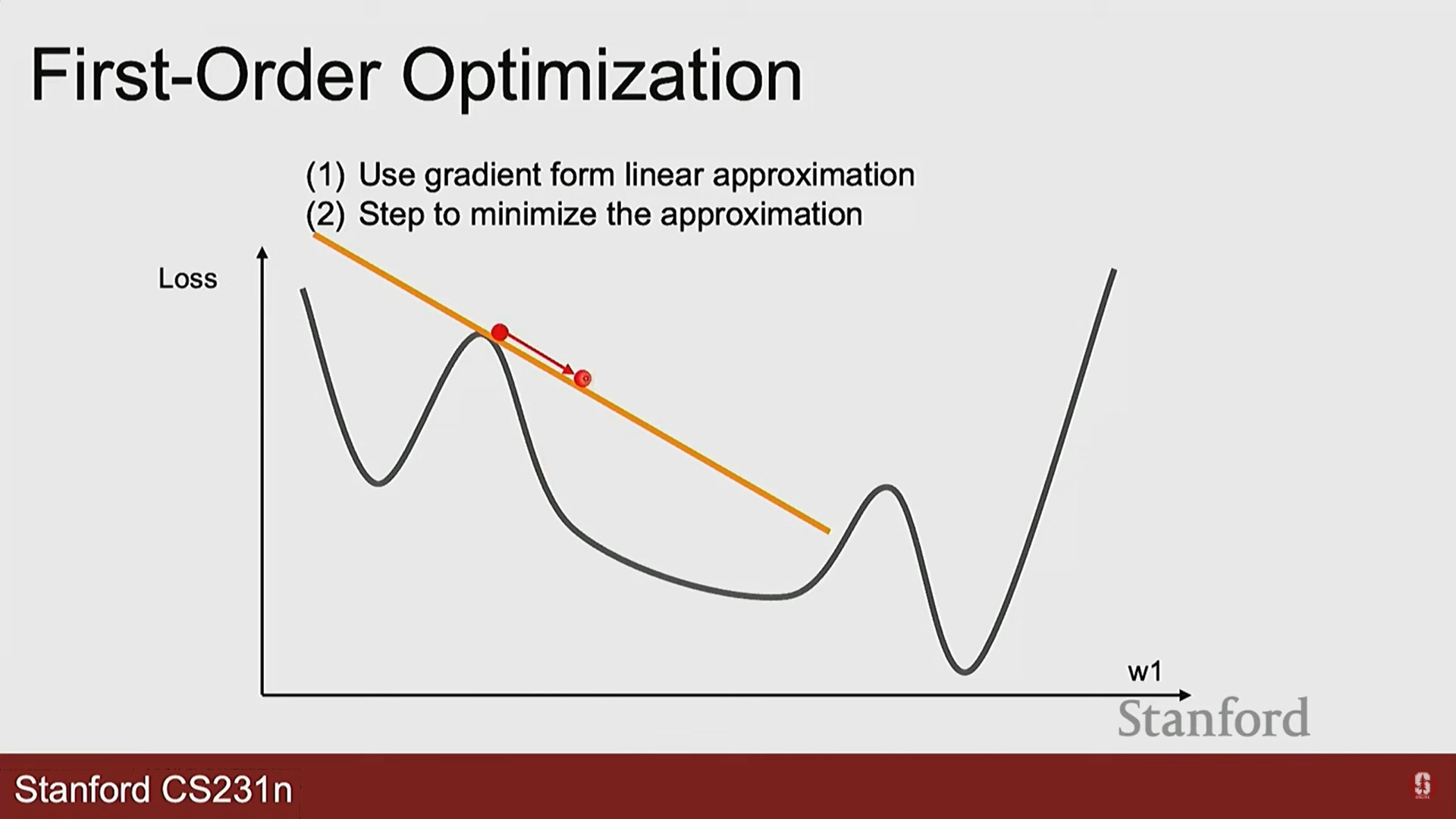
- 경사 하강법 (Gradient Descent) ⛰️: 가장 핵심적인 최적화 알고리즘입니다.
- 아이디어: 현재 위치에서 가장 가파른 내리막길 방향으로 한 걸음씩 나아가는 것을 반복합니다.

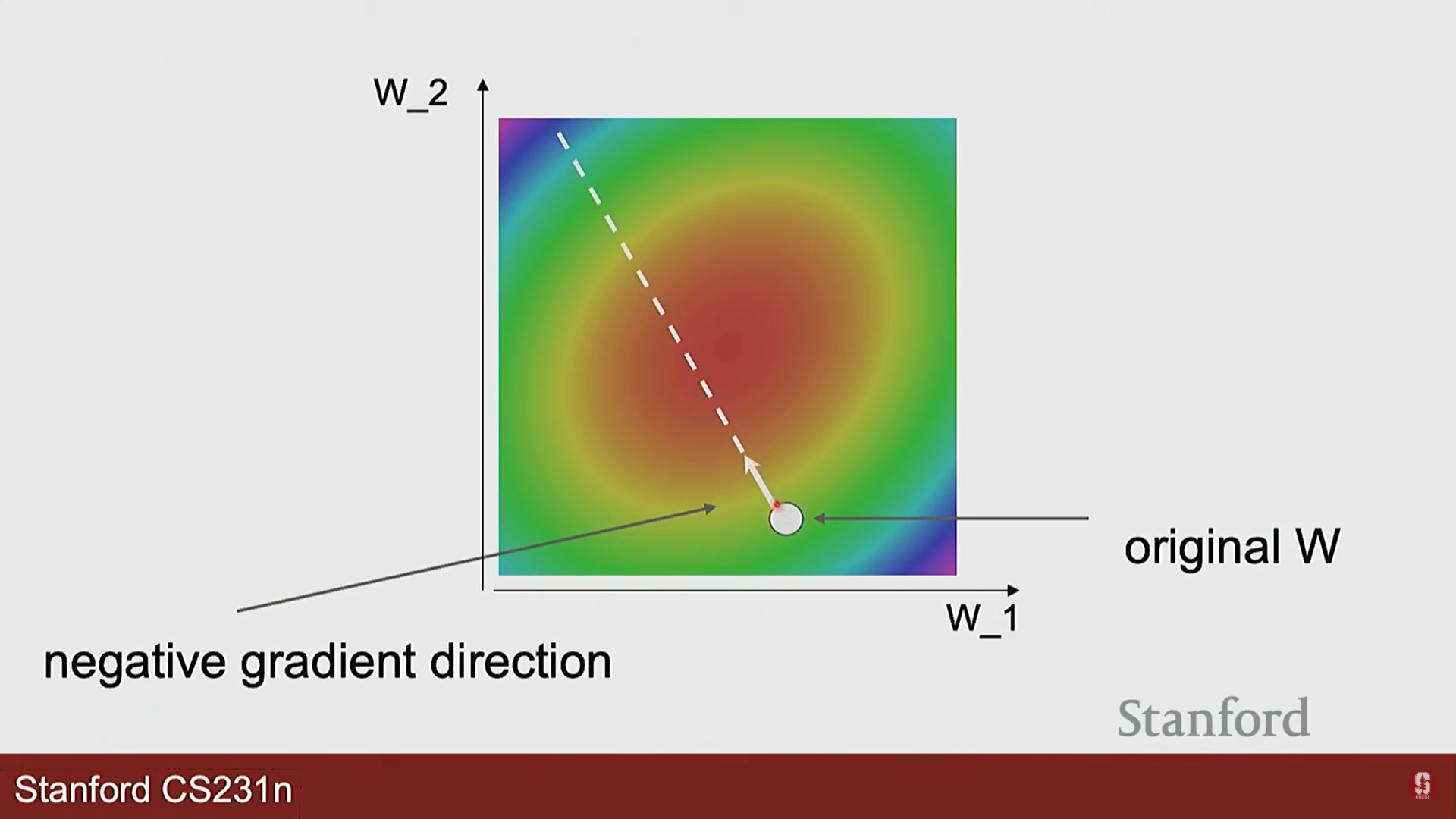
- 아이디어: 현재 위치에서 가장 가파른 내리막길 방향으로 한 걸음씩 나아가는 것을 반복합니다.
- 무작위 탐색: 가장 나쁜 방법입니다. 그냥 무작위로 W를 여러 번 시도해보고 가장 좋은 것을 고르는 방식입니다.
- 경사 하강법의 핵심, 그래디언트:
- 그래디언트(Gradient)는 손실 함수를 각 가중치로 미분한 값들의 벡터입니다.
- 이 벡터는 손실이 가장 빠르게 증가하는 방향을 가리킵니다.
- 따라서, 우리는 그래디언트의 반대 방향으로 W를 업데이트해야 손실을 줄일 수 있습니다.
- 업데이트 규칙:
dW: W에 대한 손실 함수의 그래디언트 ()learning_rate: '보폭(step size)'에 해당하는 하이퍼파라미터()로, 한 번에 얼마나 이동할지를 결정합니다.
3. 확률적 경사 하강법 (SGD)과 그 발전
- 경사 하강법의 문제점:
- 전체 학습 데이터에 대한 손실과 그래디언트를 한 번에 계산해야 합니다. 데이터가 수백만 개라면 계산량이 어마어마하고 매우 느립니다.
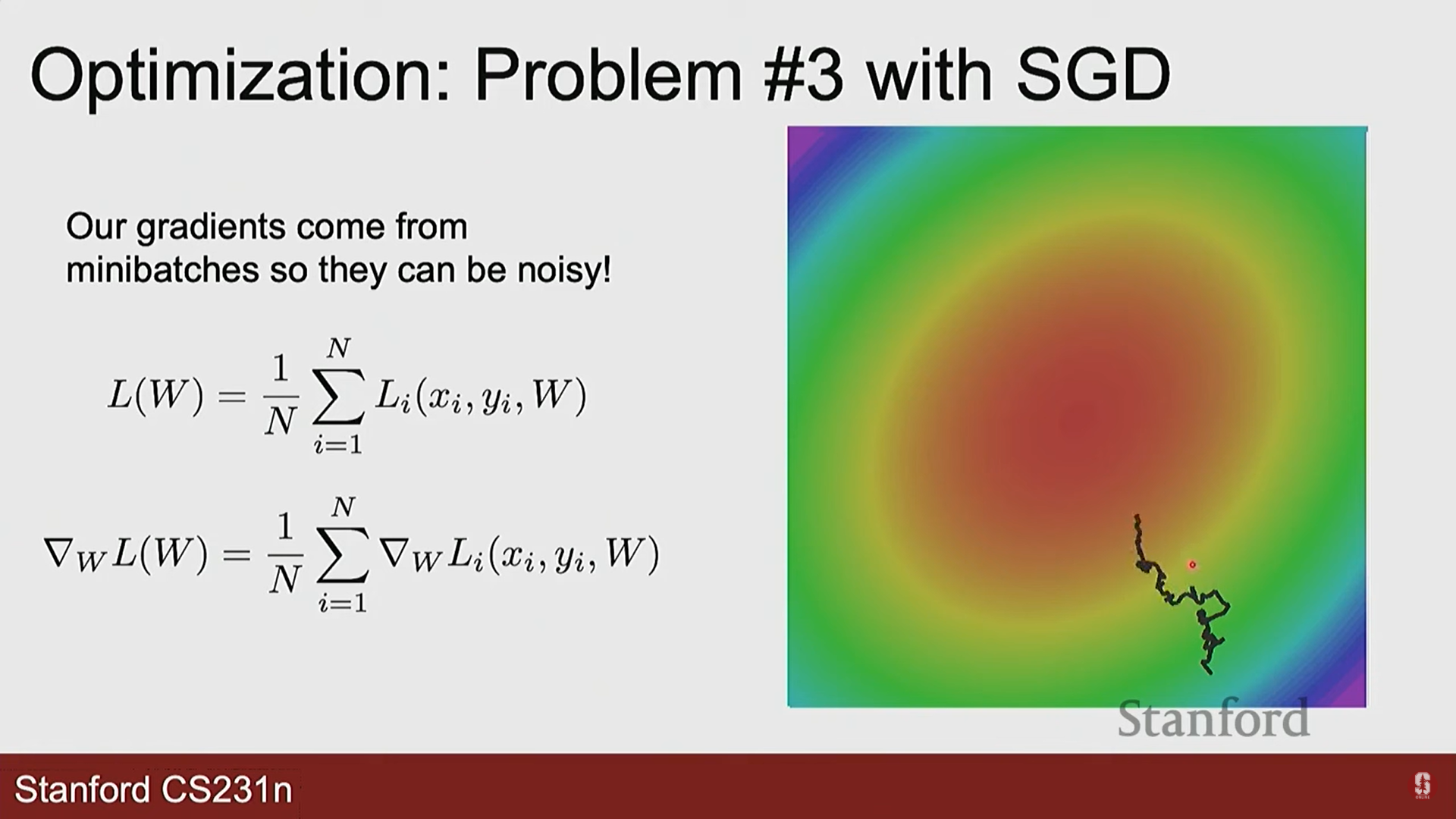
- 확률적 경사 하강법 (Stochastic Gradient Descent, SGD):
- 이 문제를 해결하기 위해, 전체 데이터 대신 미니배치(mini-batch)라는 작은 데이터 묶음(예: 32, 64, 128개)을 무작위로 뽑아 그래디언트를 근사 계산하고 파라미터를 업데이트합니다.
- 훨씬 빠르고, 노이즈가 있는 그래디언트가 오히려 지역 최솟값(local minima)을 탈출하는 데 도움을 주기도 합니다.

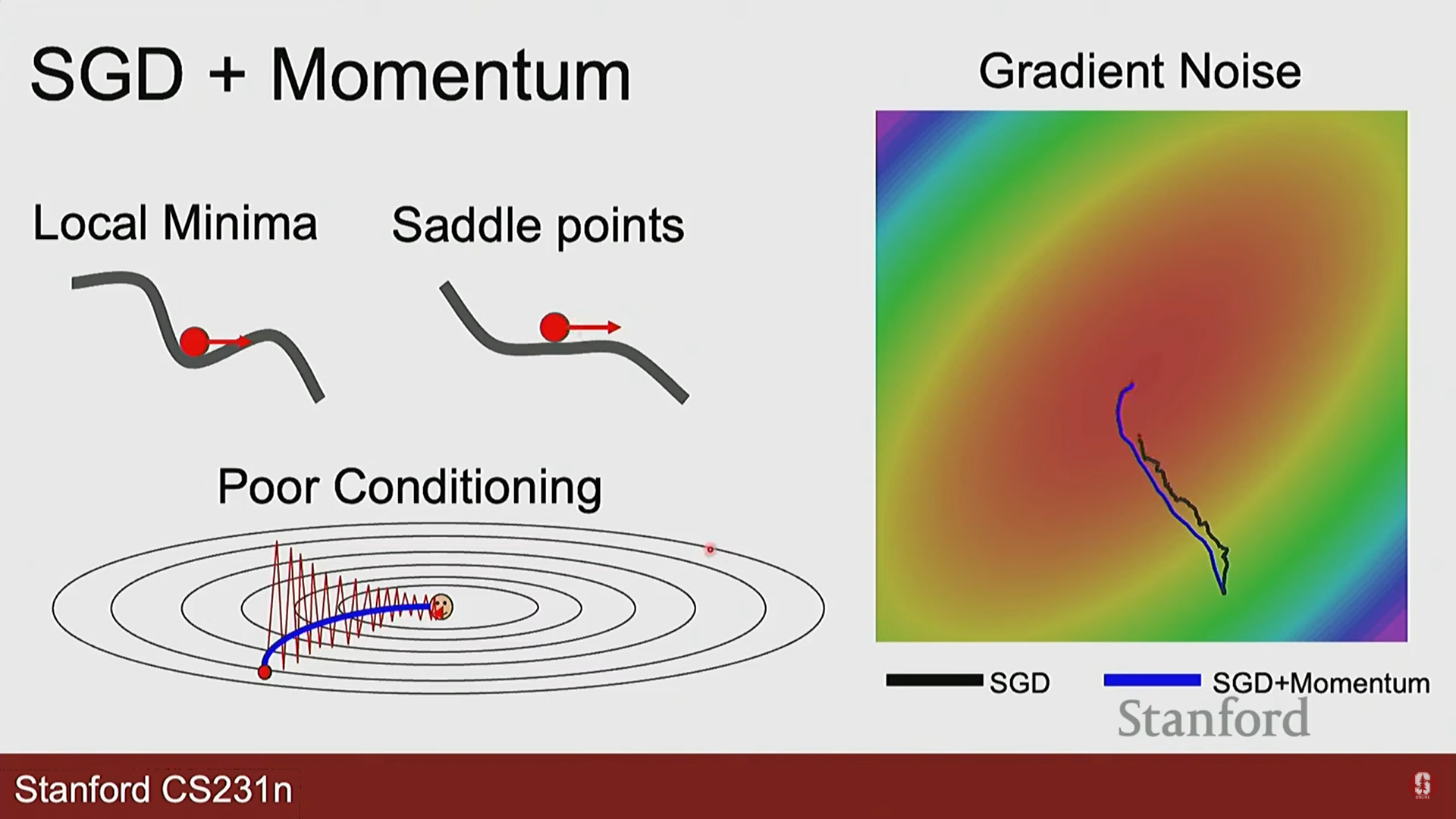
- SGD의 도전 과제들:
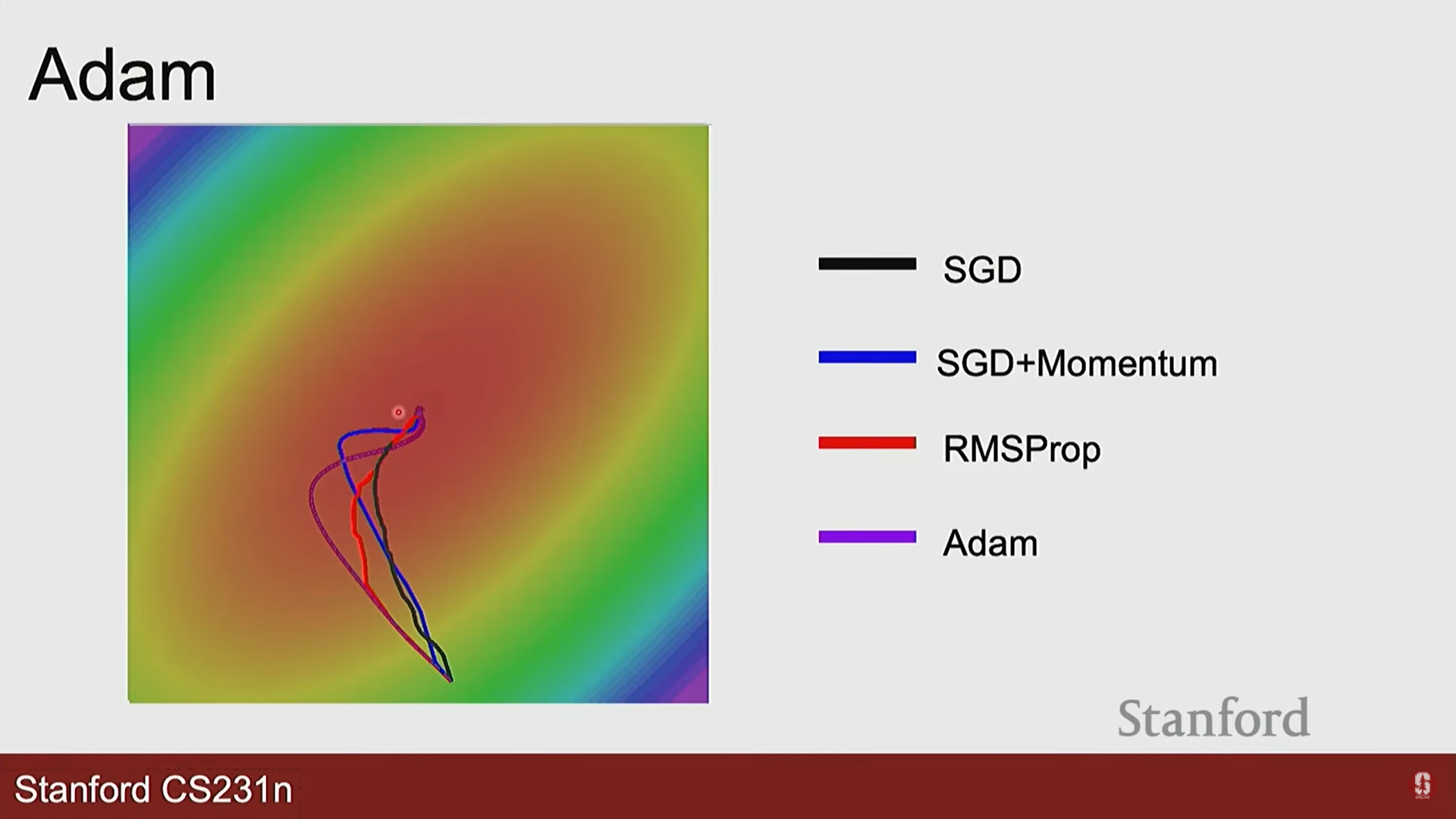
- 진동(Oscillation): 손실 지형이 한쪽은 가파르고 다른 쪽은 완만한 '계곡' 형태일 때, 최적점으로 바로 가지 못하고 양옆으로 크게 진동하며 느리게 수렴합니다.

- 지역 최솟값 & 안장점(Saddle Point): 그래디언트가 0이 되는 지점에 갇혀 업데이트가 멈출 수 있습니다.
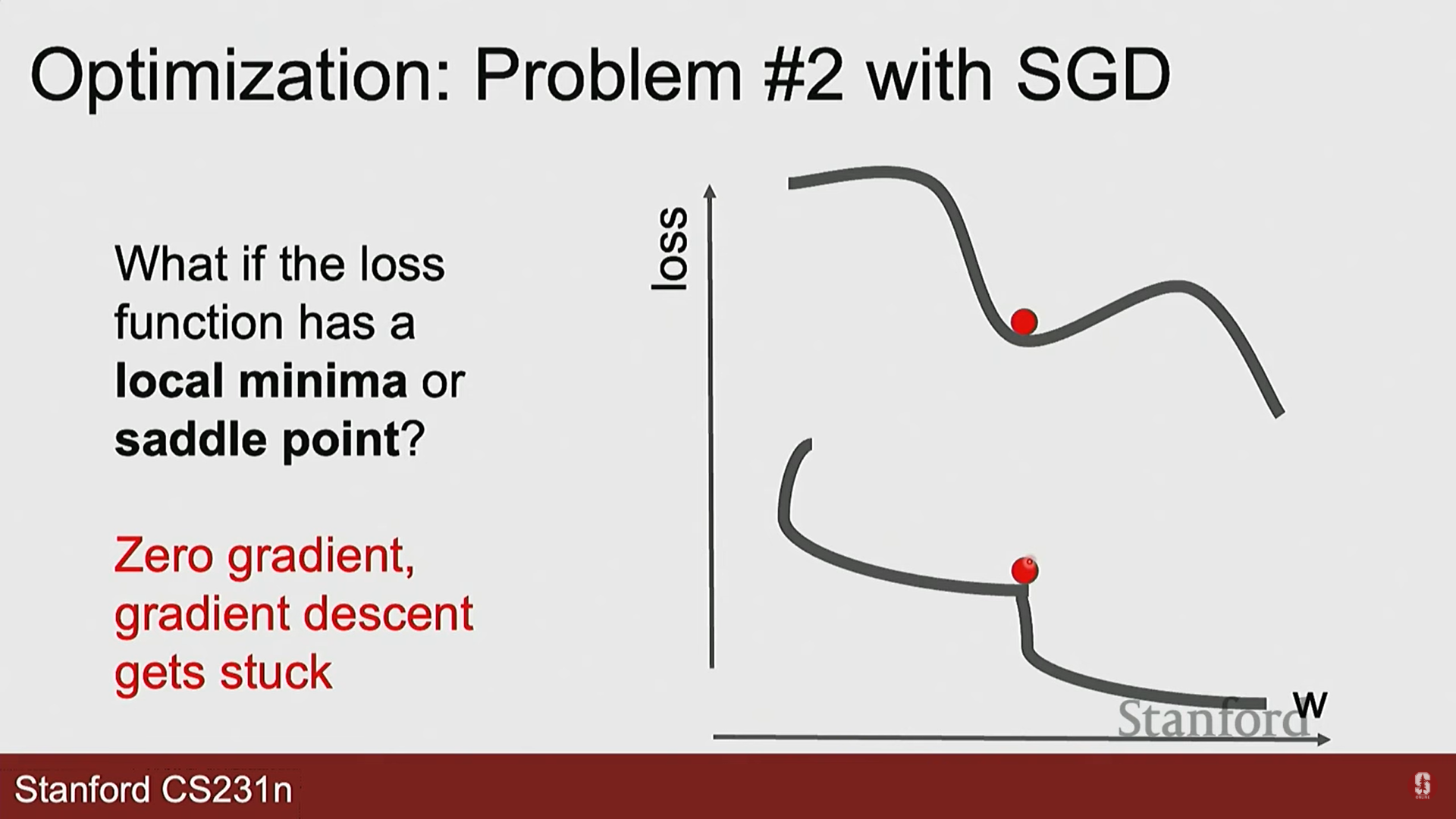
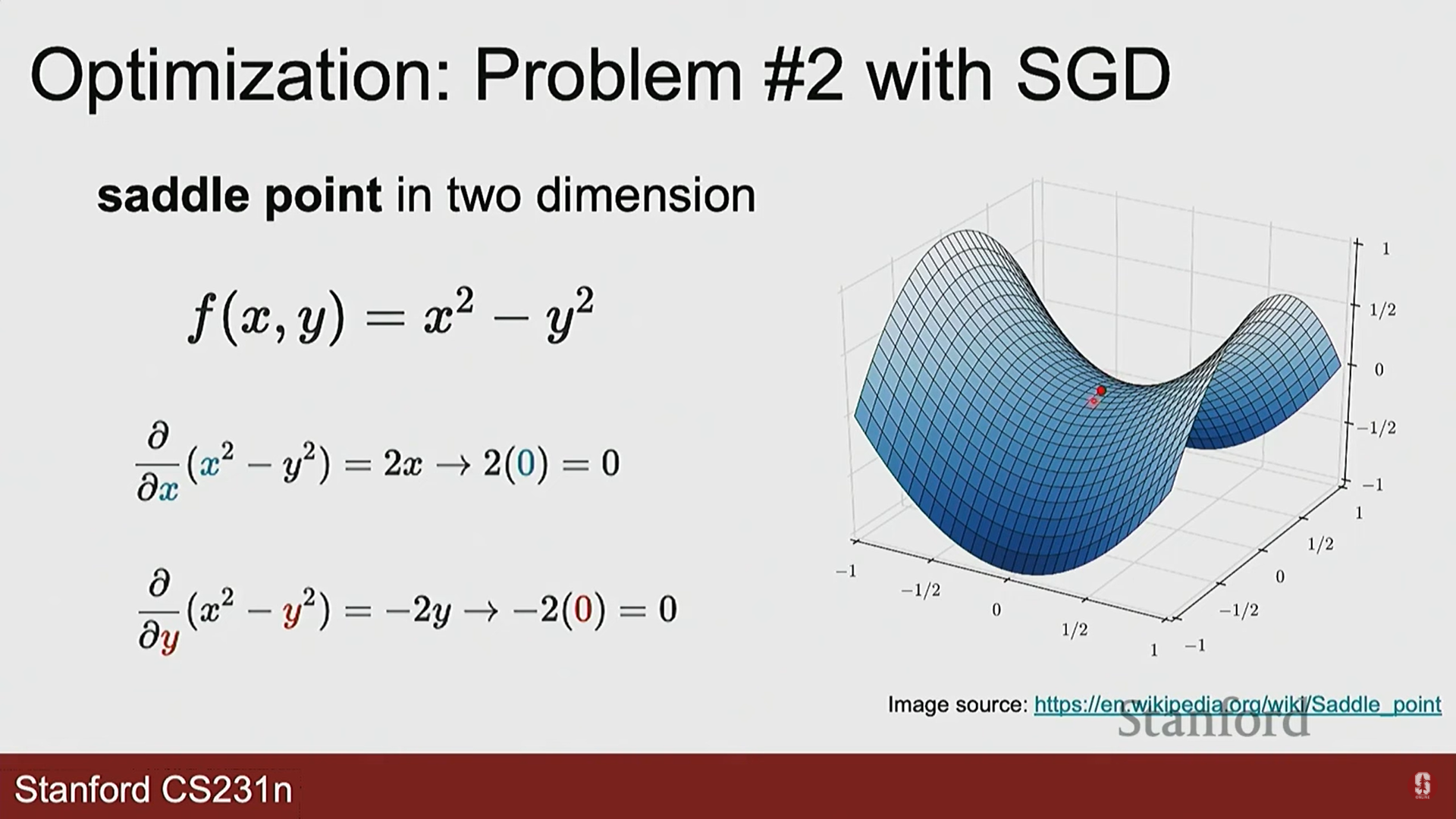
- 진동(Oscillation): 손실 지형이 한쪽은 가파르고 다른 쪽은 완만한 '계곡' 형태일 때, 최적점으로 바로 가지 못하고 양옆으로 크게 진동하며 느리게 수렴합니다.
- SGD 개선을 위한 알고리즘들:
- 모멘텀 (Momentum):
- 물리적 비유: 언덕을 굴러 내려가는 공처럼, 이전에 이동하던 방향에 관성(momentum)을 더합니다.
- 업데이트 수식:
- 작동 방식: 그래디언트의 이동 평균(moving average)을 계산하여 현재 그래디언트와 합쳐 업데이트 방향을 결정합니다.
- 효과: 진동을 줄여주고, 안장점이나 완만한 지역 최솟값을 관성으로 통과할 수 있게 도와줍니다. 평균을 이용하니까, 진동은 중심에 맞춰지고, 이동방향을 그대로 남게 되어 optimum으로 향하게 됩니다.

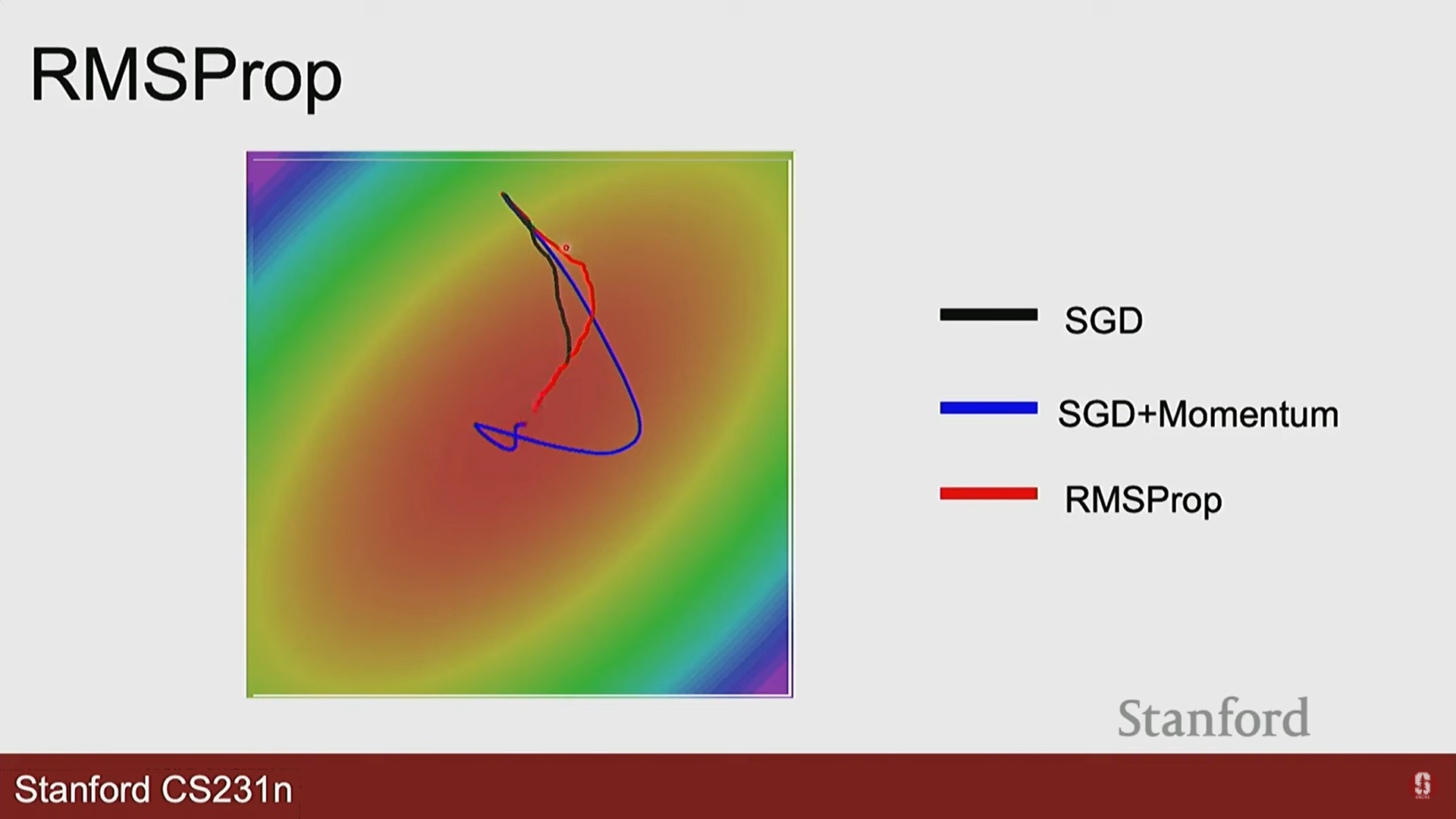
- RMSprop (Root Mean Square Propagation):
- 아이디어: 감쇠율 을 활용하고, 그래디언트의 크기에 따라 학습률을 적응적으로 조절합니다.
- 업데이트 수식:
- 작동 방식: 그래디언트의 제곱값에 대한 이동 평균을 계산하고, 이 값의 제곱근으로 학습률을 나눕니다.
- 효과: 그래디언트를 제곱하여 방향을 제외한 각 방향에 대한 크기(진동이 심한 정도)를 파악할 수 있고, 이를 통해 나눔으로 특정 그래디언트가 컸던 방향(진동이 심한 방향)은 보폭을 줄이고, 그래디언트가 작았던 방향(완만한 방향)은 보폭을 늘려(왜냐하면 작은 값으로 나누면 상대적으로 커지는 효과) 계곡 문제를 효과적으로 해결합니다.


- Adam (Adaptive Moment Estimation):
- 결합: 모멘텀과 RMSprop의 장점을 합친, 현재 가장 널리 사용되는 최적화 알고리즘입니다.
- 업데이트 수식:
- 작동 방식: 그래디언트의 1차 모멘트(평균, 모멘텀)와 2차 모멘트(제곱의 평균, RMSprop)를 모두 추적하여 업데이트를 수행합니다.


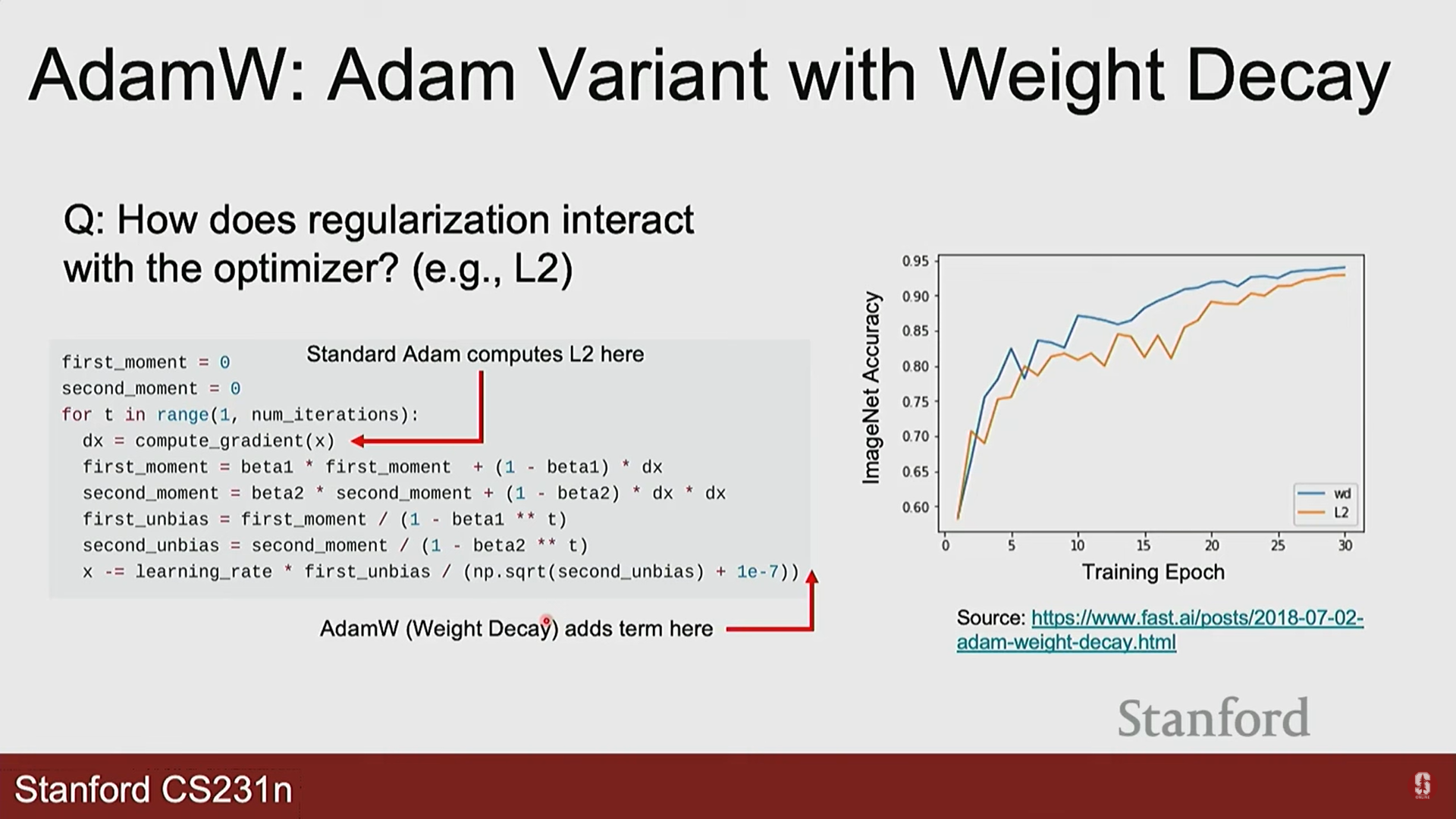
- AdamW: Adam에 L2 정규화(가중치 감쇠)를 더 효과적으로 적용한 개선된 버전입니다.


- 모멘텀 (Momentum):
4. 학습률 스케줄링과 2차 최적화
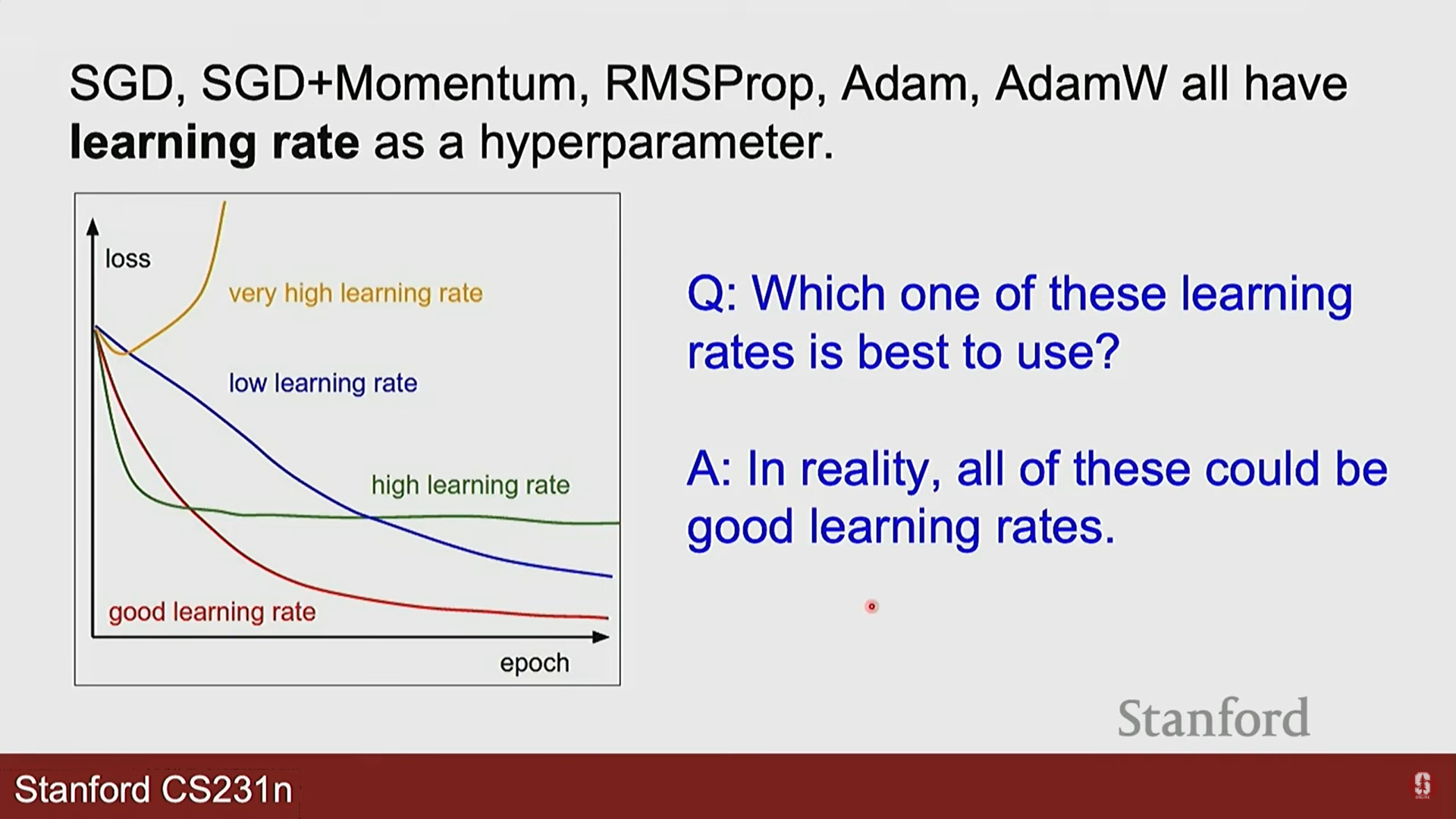
- 학습률 (Learning Rate)의 중요성:
- 너무 크면: 최적점을 지나쳐 발산(diverge)할 수 있습니다.
- 너무 작으면: 학습이 매우 느리고, 지역 최솟값에 갇히기 쉽습니다.
- 학습률 스케줄링 (Learning Rate Scheduling):
- 학습 과정 동안 학습률을 동적으로 조절하는 전략입니다.
- 일반적인 전략: 학습 초기에는 큰 학습률로 빠르게 최적점에 다가가고, 최적점 근처에서는 학습률을 줄여 미세 조정을 합니다.
- 대표적인 스케줄러:
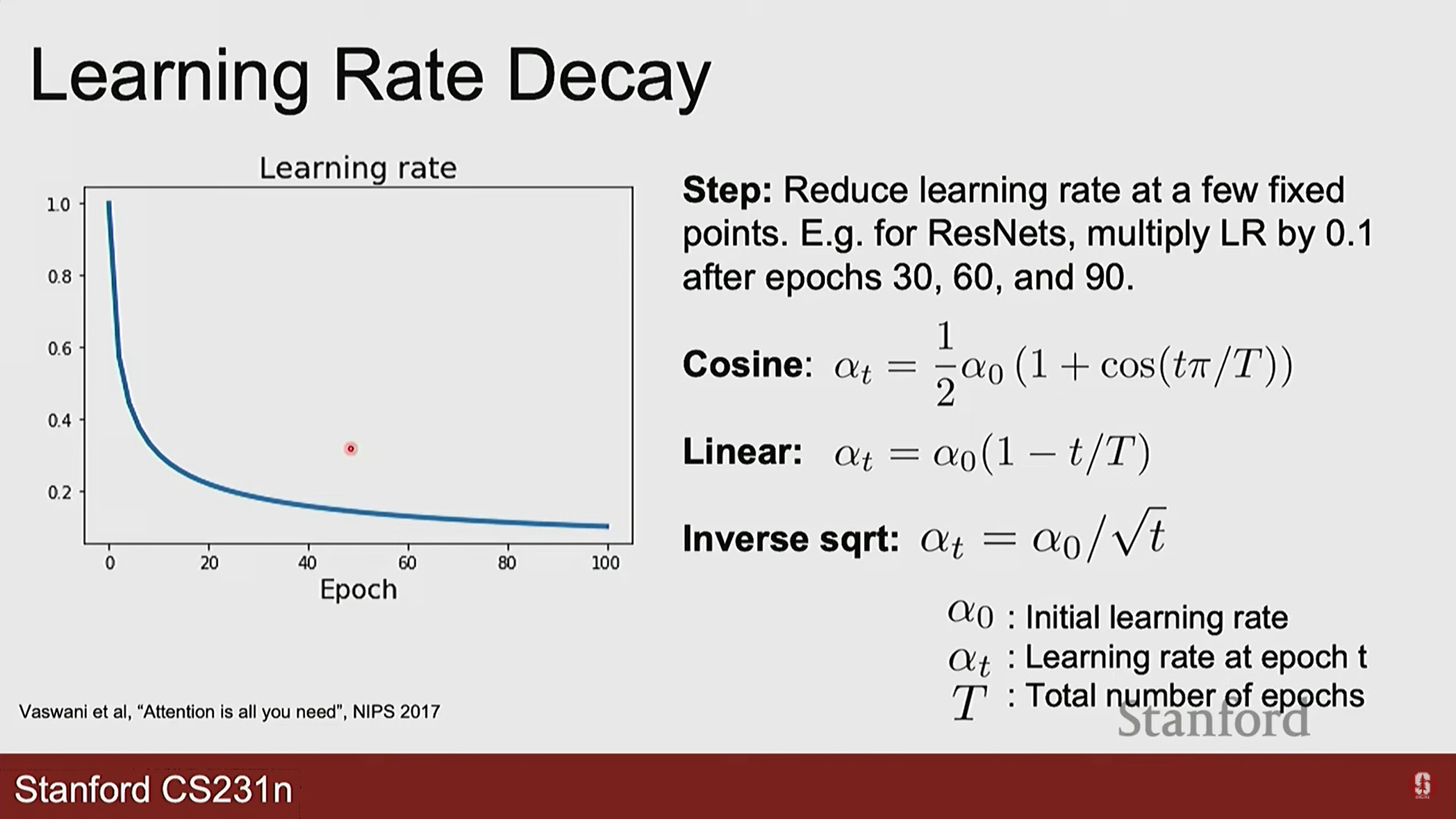
- 스텝 감쇠(Step Decay): 특정 epoch마다 학습률을 일정 비율로 줄입니다.
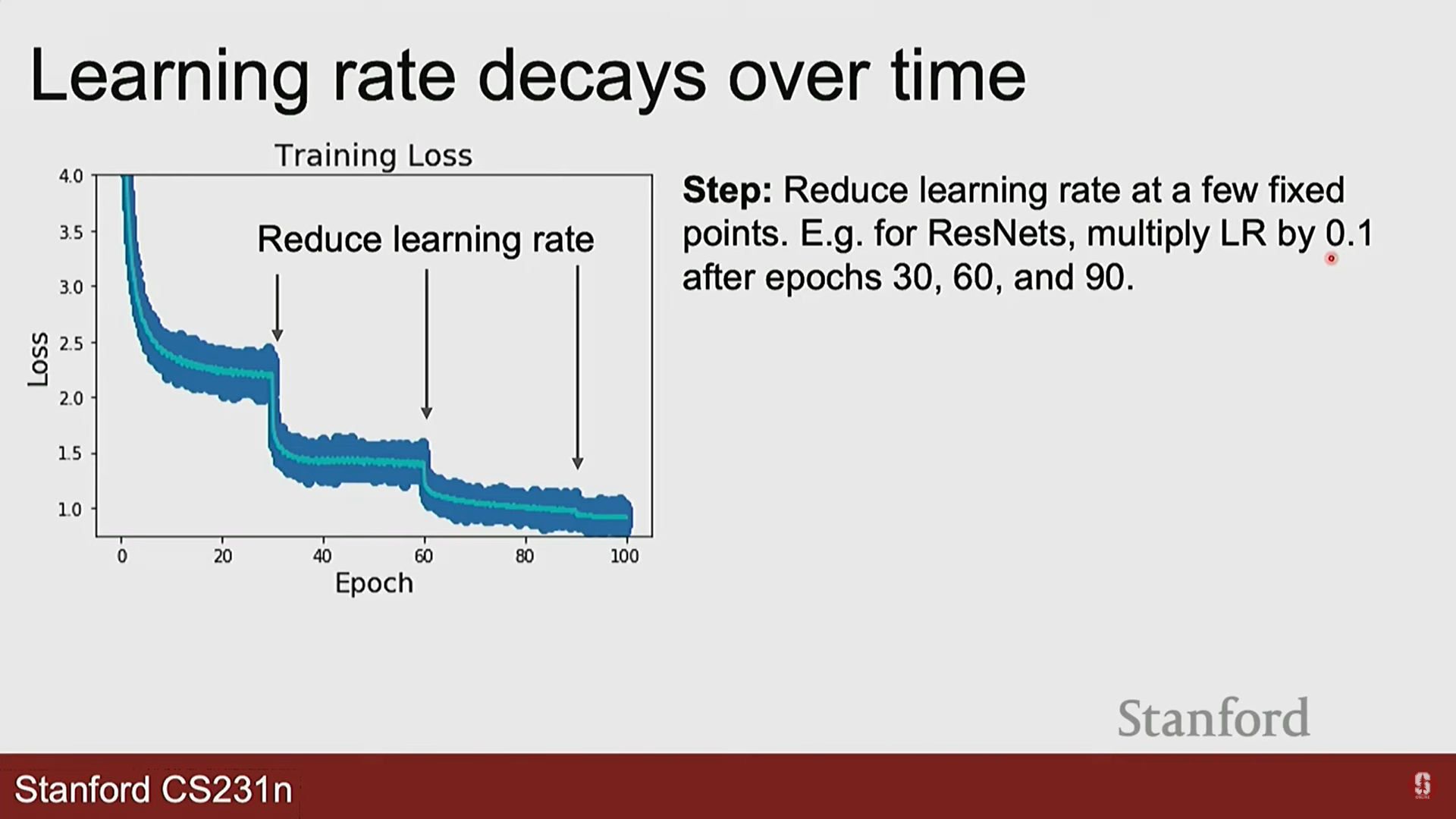
- 코사인 감쇠(Cosine Decay): 코사인 함수 모양으로 학습률을 부드럽게 줄여나갑니다.
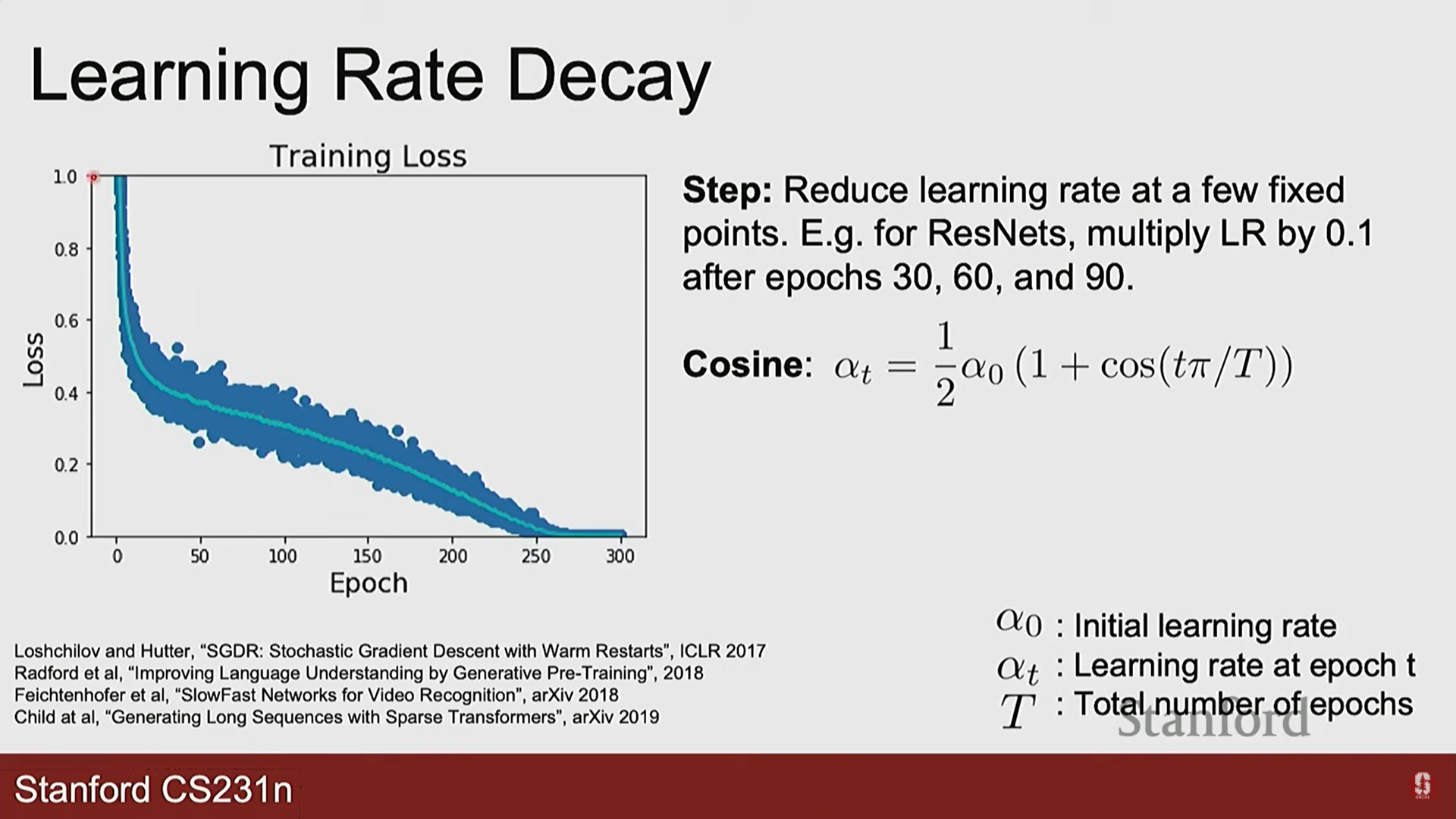
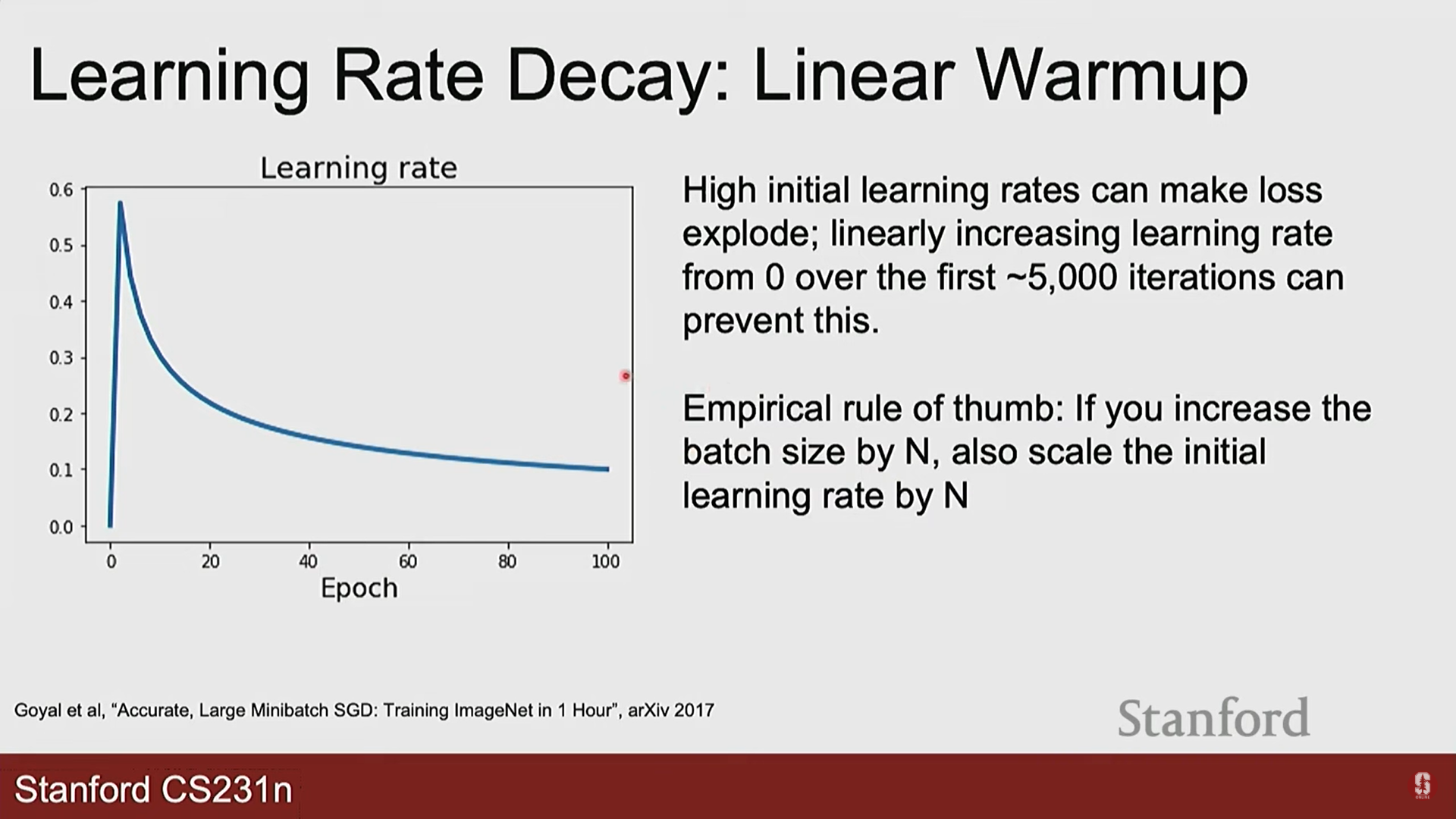
- 선형 웜업(Linear Warm-up): 불안정한 학습 초기에 학습률을 0에서부터 서서히 증가시켜 안정성을 높입니다.
- 스텝 감쇠(Step Decay): 특정 epoch마다 학습률을 일정 비율로 줄입니다.
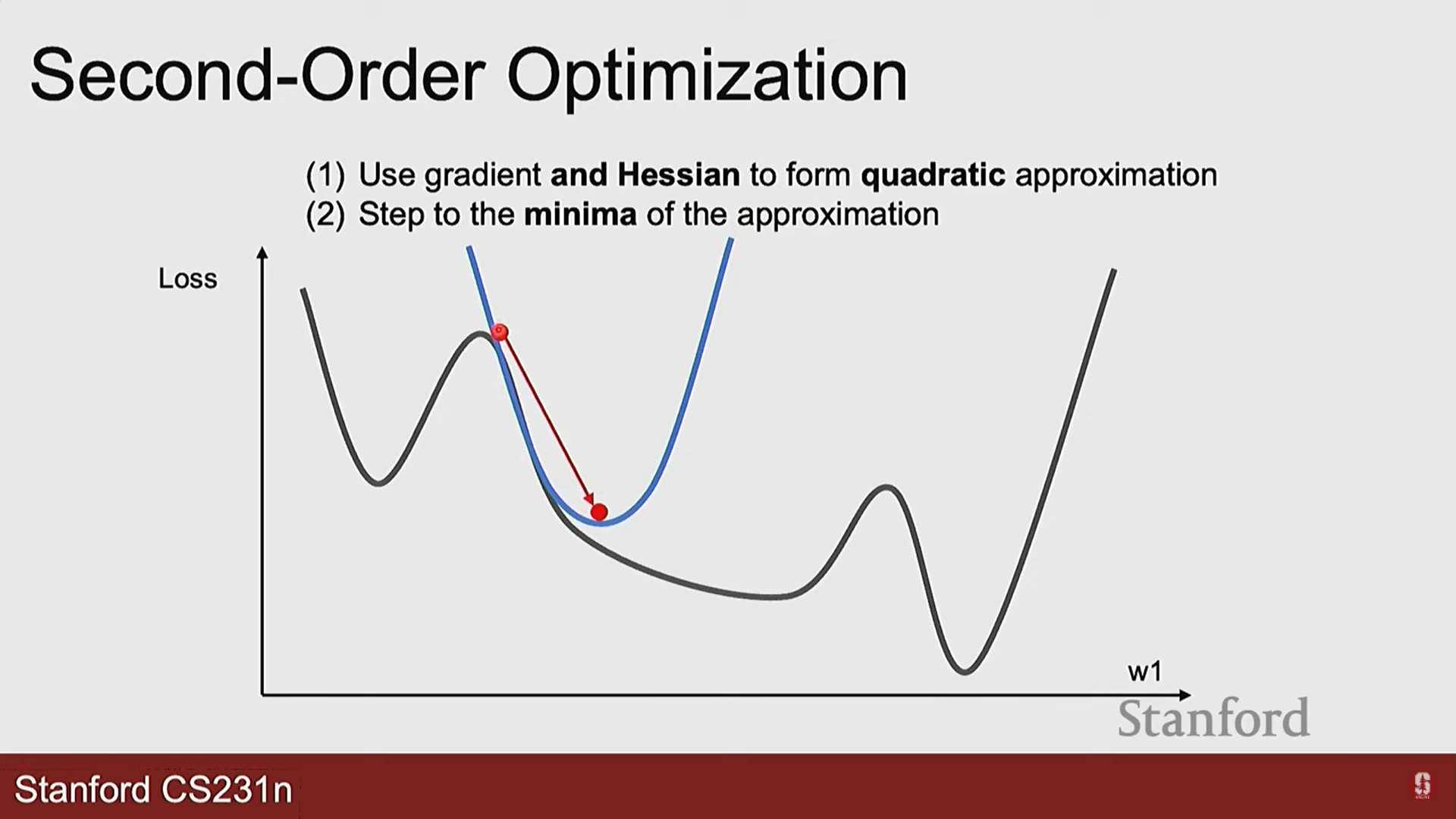
- 2차 최적화 (Second-Order Optimization):
- 개념: 그래디언트(1차 미분)뿐만 아니라 헤시안(Hessian) 행렬(2차 미분)을 사용하여 손실 함수의 '곡률'까지 파악하는 방법입니다.
- 장점: 손실 지형에 대한 더 많은 정보를 활용하므로 더 빠르고 정확하게 최적점에 도달할 수 있습니다.
- 단점: 헤시안 행렬을 계산하고 저장하는 비용이 파라미터 개수의 제곱에 비례하여 매우 크기 때문에, 수백만 개 이상의 파라미터를 가진 현대의 딥러닝 모델에는 거의 사용되지 않습니다.

5. 심화 내용: 최적화 알고리즘의 본질
- 기술적 배경: 모든 1차 최적화 알고리즘(SGD, Adam 등)의 근본적인 목표는 고차원의 복잡한 손실 함수 표면에서 전역 최솟값(global minimum)을 찾는 것입니다. 하지만 그래디언트 정보만으로는 현재 위치가 지역 최솟값인지, 안장점인지, 아니면 거대한 평지(plateau)인지 구분하기 어렵습니다. 모멘텀과 적응적 학습률(adaptive learning rate)은 이러한 불확실한 지형을 더 빠르고 안정적으로 탐색하기 위해 과거의 정보를 '기억'하고 미래의 보폭을 '조절'하는 정교한 경험적 기법(heuristic)이라고 할 수 있습니다.
- 최신 동향: 최근에는 Adam이 표준처럼 사용되지만, 때로는 잘 튜닝된 SGD+모멘텀이 더 좋은 일반화 성능을 보이는 경우가 있다는 연구 결과도 많습니다. 이는 Adam이 너무 빨리 최적점에 수렴하여, 날카롭고 좁은 최솟값(sharp minima)에 빠지는 경향이 있기 때문이라는 분석이 있습니다. 반면 SGD는 노이즈 덕분에 더 넓고 평평한 최솟값(flat minima)을 찾아내고, 이것이 더 나은 일반화로 이어진다는 것입니다. 이처럼 '어떤 최적화 알고리즘이 항상 최고인가'에 대한 정답은 없으며, 문제와 데이터에 따라 최적의 선택이 달라질 수 있습니다.
- 명확한 한계점: 본 강의에서 다룬 모든 최적화 기법들은 손실 함수가 볼록(convex)하지 않은 비볼록(non-convex) 함수라는 근본적인 문제에 직면합니다. 이는 우리가 찾은 해가 전역 최적해라는 보장이 전혀 없다는 것을 의미합니다. 딥러닝에서 '최적화에 성공했다'는 것은 보통 손실 값이 충분히 낮아져 검증 세트에서 좋은 성능을 보이는 '쓸만한' 지역 최솟값을 찾았다는 의미로 사용됩니다. 전역 최적해를 찾는 것은 여전히 이론적으로 매우 어려운 미해결 과제입니다.