1. 순환 신경망(RNN)의 개념
1) 순차적 데이터 모델링의 필요성
- 이전 강의에서 다룬 CNN과 같은 모델들은 이미지처럼 고정된 크기의 입력을 가정합니다. 하지만 현실 세계의 많은 데이터는 문장, 음성, 주식 가격처럼 길이가 가변적인 순서가 있는 데이터(시퀀스)입니다. 이러한 데이터를 처리하기 위해 순환 신경망이 고안되었습니다.
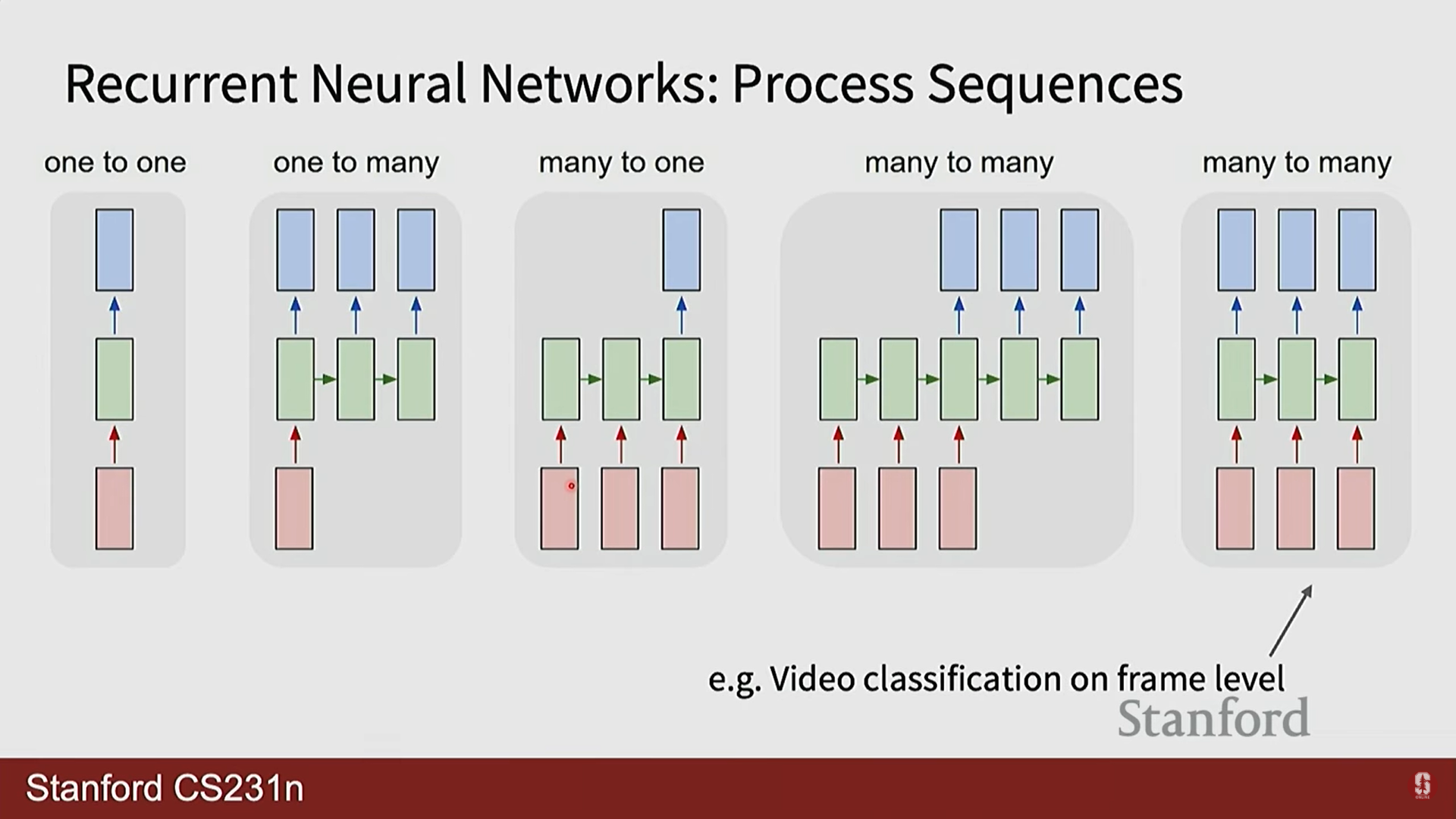
- 시퀀스 모델링의 유형:
- 일대다(One-to-Many): 하나의 입력에서 여러 개의 출력을 생성합니다. (예: 이미지 캡셔닝)
- 다대일(Many-to-One): 여러 개의 입력에서 하나의 출력을 생성합니다. (예: 비디오 분류)
- 다대다(Many-to-Many): 여러 개의 입력에서 여러 개의 출력을 생성합니다. (예: 비디오 프레임별 분류)
2) RNN의 기본 구조와 원리
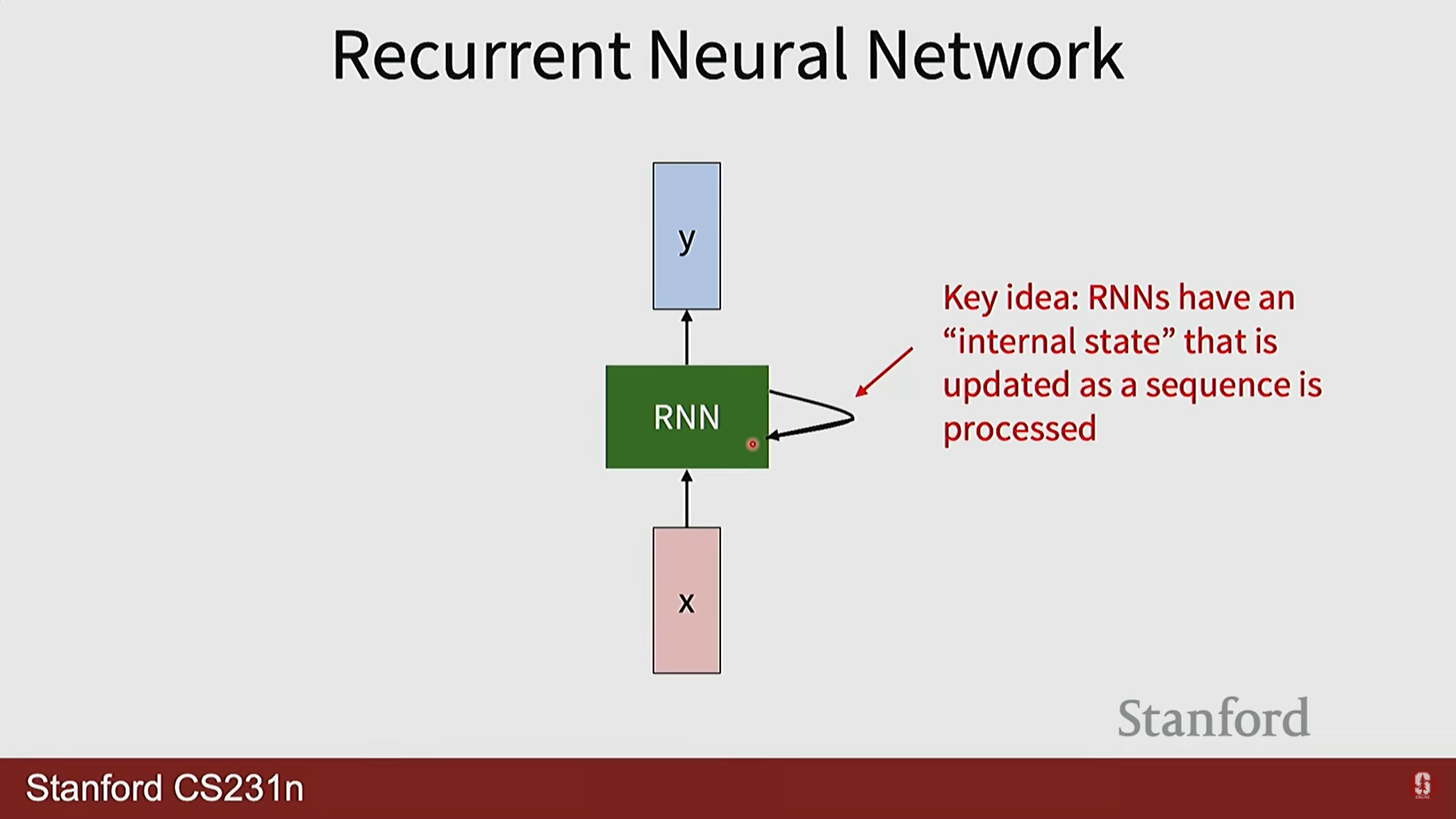
- RNN의 핵심 아이디어는 네트워크 내에 정보를 기억하는 순환 루프(loop)를 두는 것입니다. 각 시점(time step)에서 네트워크는 현재 입력()과 이전 시점의 기억()을 함께 받아 현재 시점의 기억()을 갱신합니다.
- 이 '기억'에 해당하는 것이 바로 은닉 상태(hidden state)이며, 과거 시점들의 정보를 요약하여 미래를 예측하는 데 사용되는 핵심적인 문맥(context) 역할을 수행합니다.
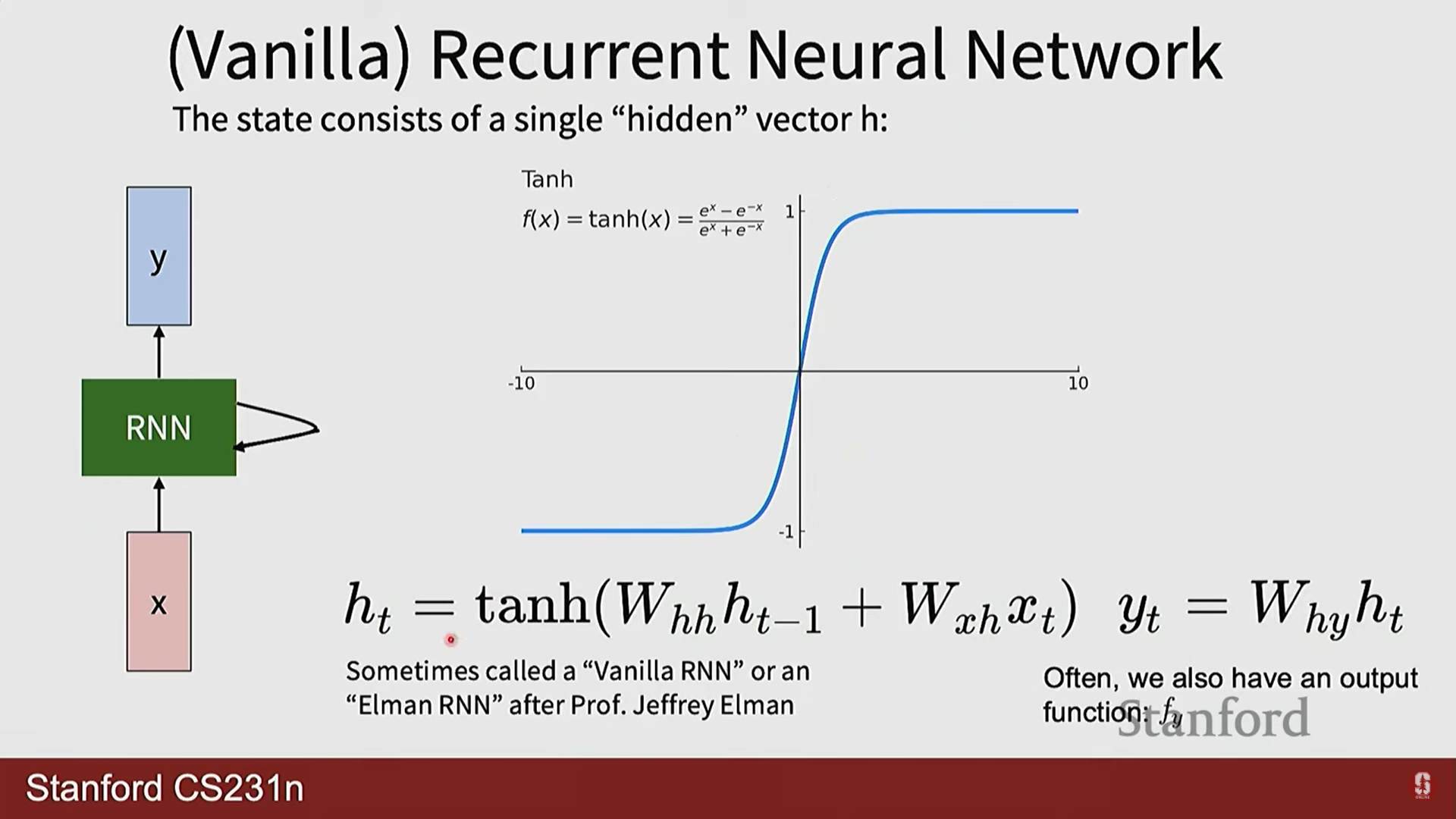
- 수학적 표현: 바닐라(Vanilla) RNN의 은닉 상태와 출력은 다음과 같은 재귀적(recurrent) 관계로 정의됩니다.
- : 모든 시점에서 동일하게 사용되는(shared) 가중치 행렬입니다. 이 '가중치 공유' 매커니즘 덕분에 RNN은 입력 시퀀스의 길이에 구애받지 않고 유연하게 작동할 수 있습니다.
- : 첫 번째 은닉 상태를 계산하기 위한 초기 은닉 상태이며, 보통 0 벡터로 초기화합니다.



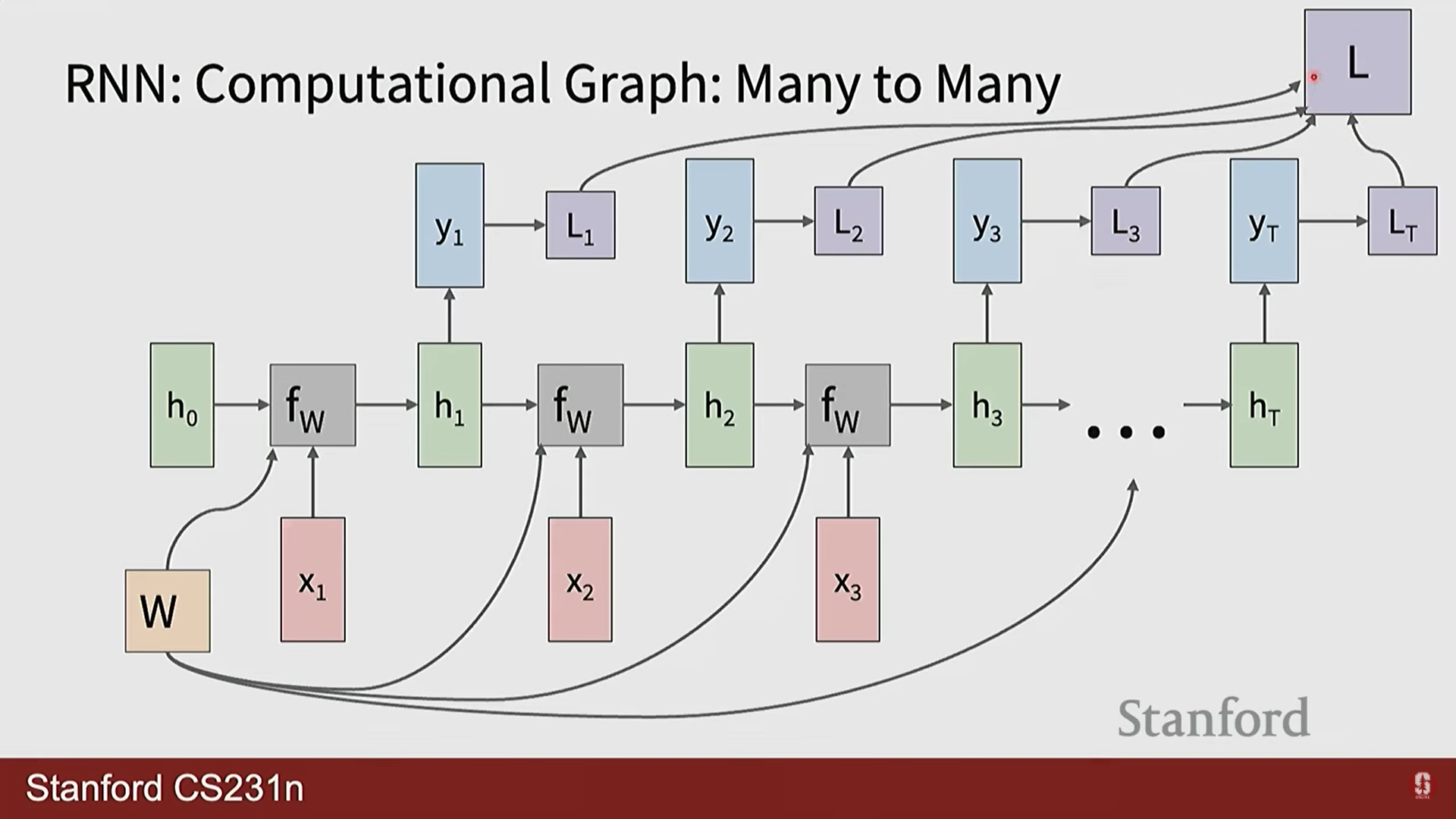
부연설명
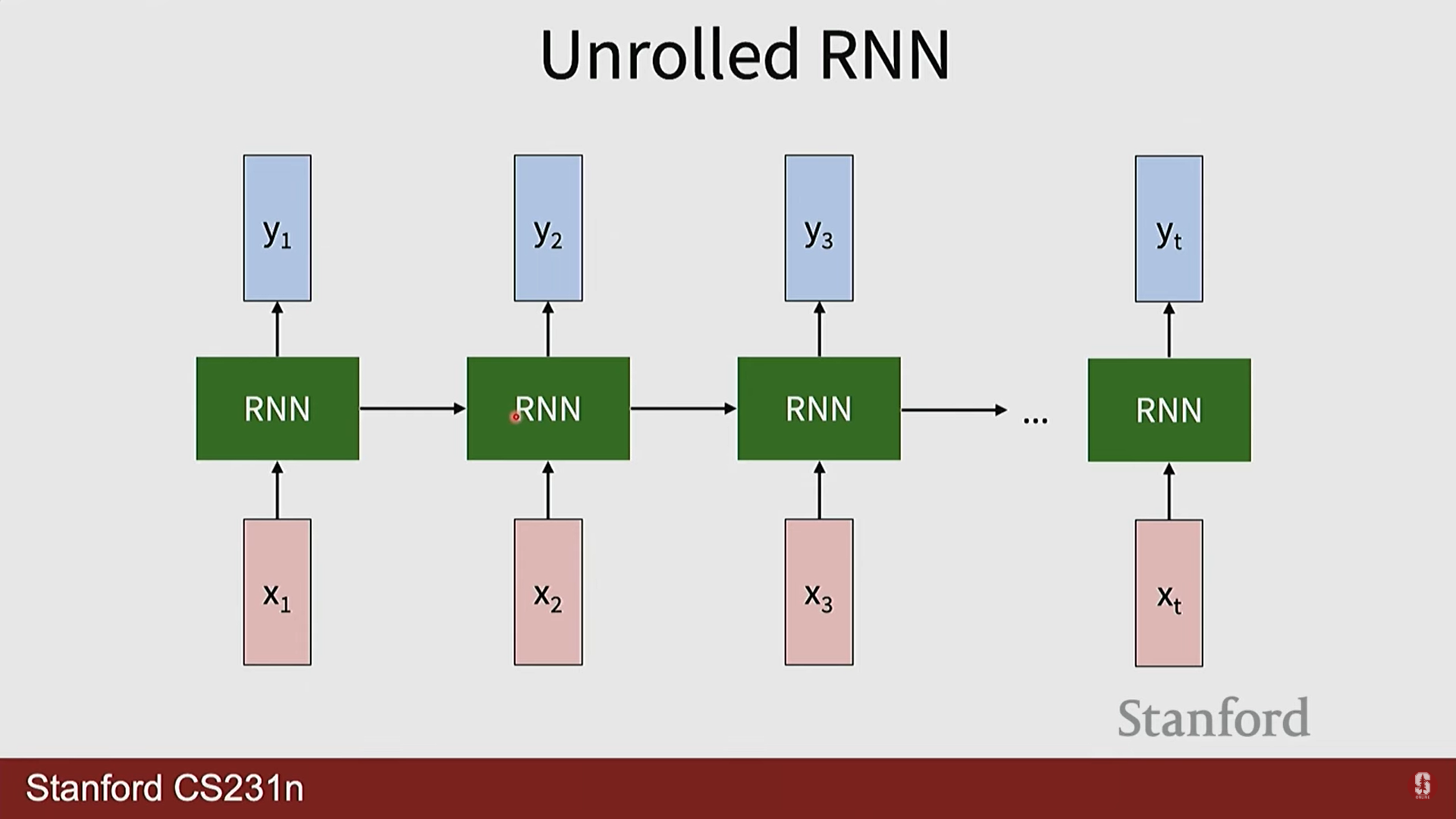
- RNN의 순환 구조 다이어그램은 이해하기 복잡할 수 있어, 보통 시간을 따라 쭉 펼쳐진(unrolled) 형태로 많이 표현합니다. 이 펼쳐진 다이어그램을 보면, 동일한 함수와 가중치 가 각 시점에서 반복적으로 적용되는 것을 명확하게 볼 수 있으며, 이것이 RNN의 핵심 원리입니다.
2. RNN의 학습과 응용
1) BPTT (Backpropagation Through Time)
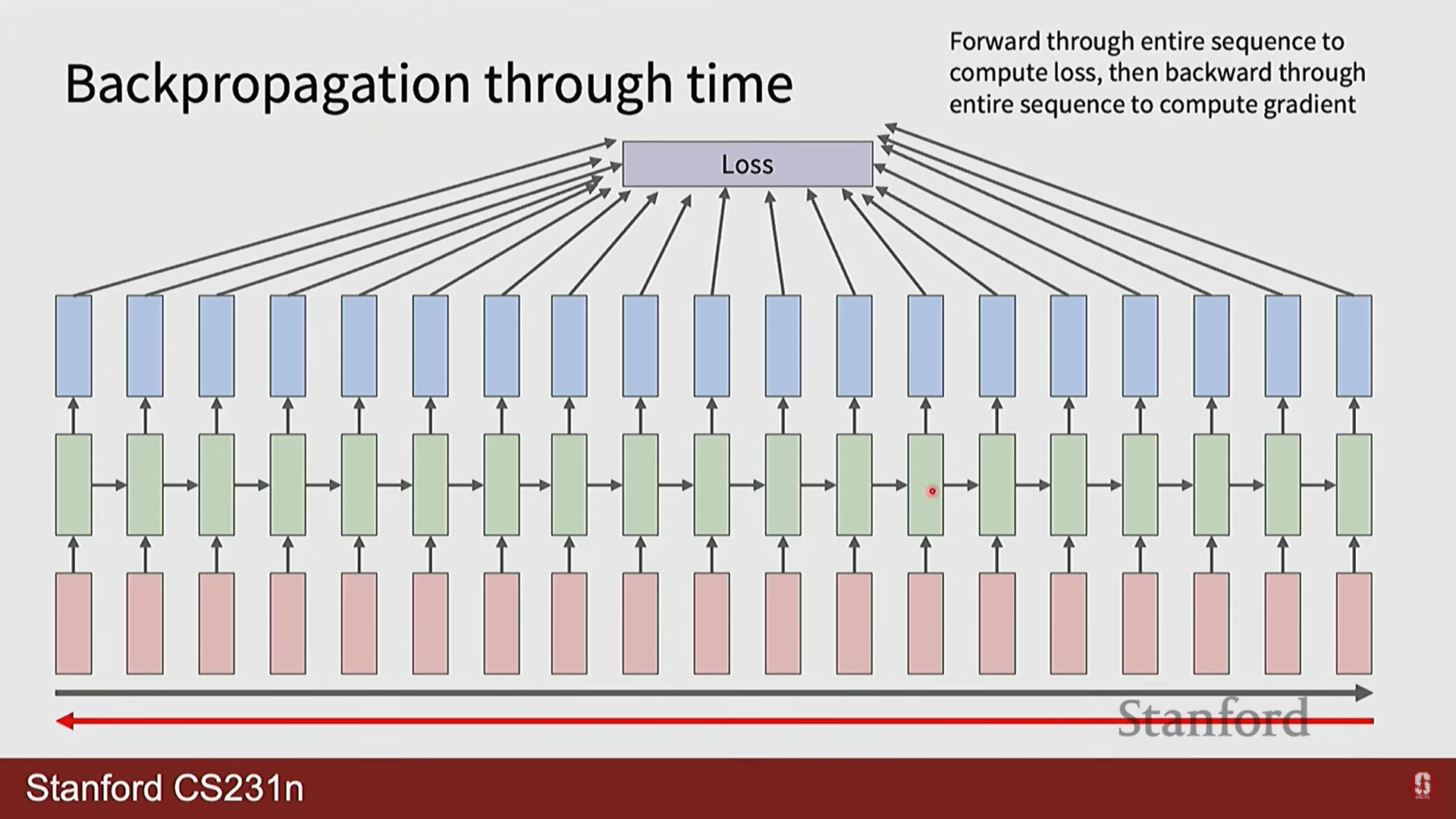
- RNN의 학습은 시간을 따라 펼쳐진 네트워크 구조에 역전파 알고리즘을 적용하는 BPTT(시간을 통한 역전파)를 통해 이루어집니다.
- 학습 과정:
- 순전파(Forward Pass): 시퀀스의 시작부터 끝까지 순차적으로 은닉 상태와 출력을 계산합니다.
- 손실 계산(Loss Calculation): 각 시점의 출력()과 실제 정답() 간의 손실()을 계산하고, 시퀀스 전체의 총 손실은 이들을 모두 합산합니다.
- 역전파(Backward Pass): 총 손실을 각 가중치로 미분하여 기울기를 계산합니다. 가중치는 모든 시점에서 공유되므로, 최종 기울기는 각 시점에서 계산된 기울기를 모두 더하여 구합니다.
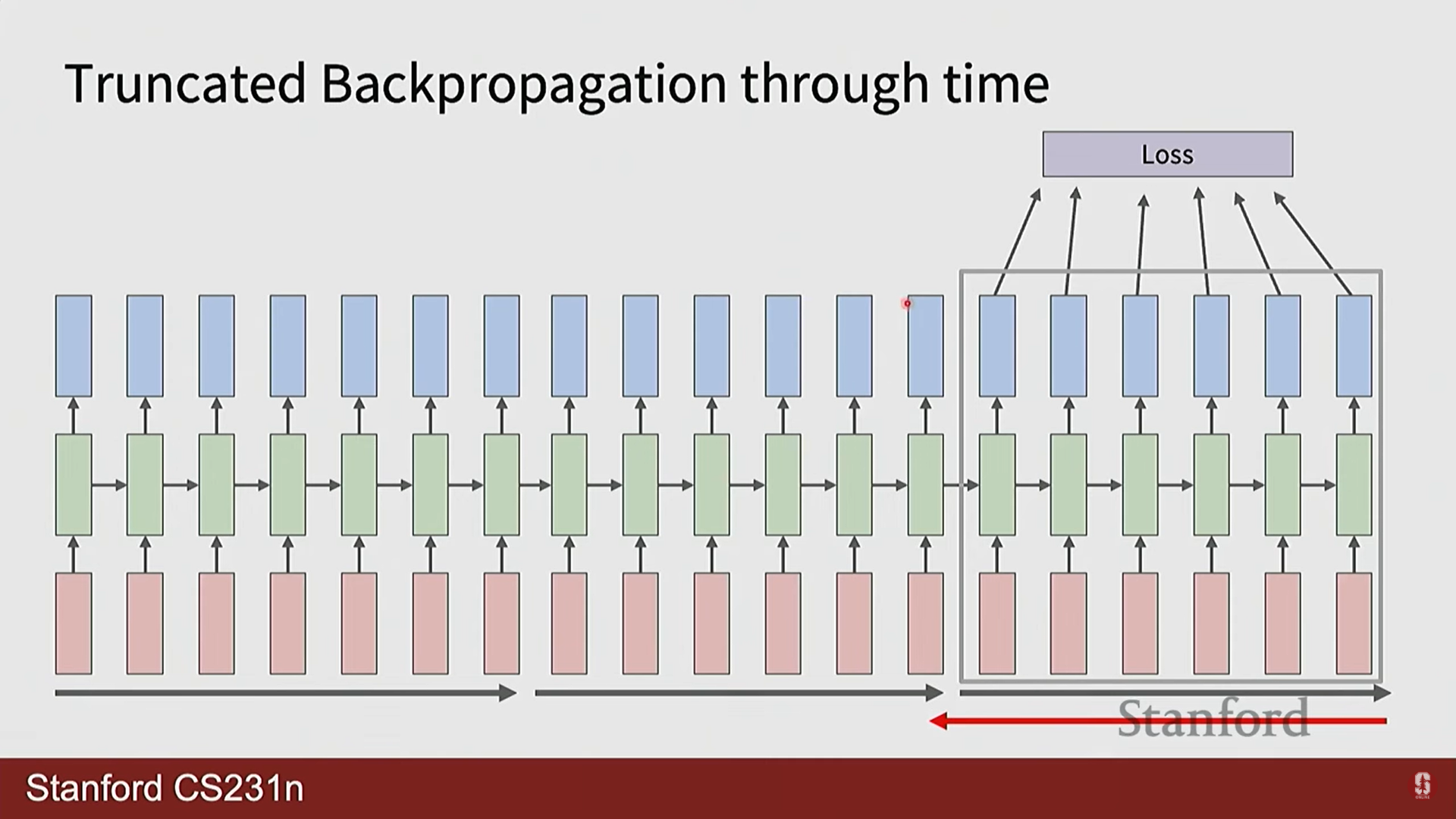
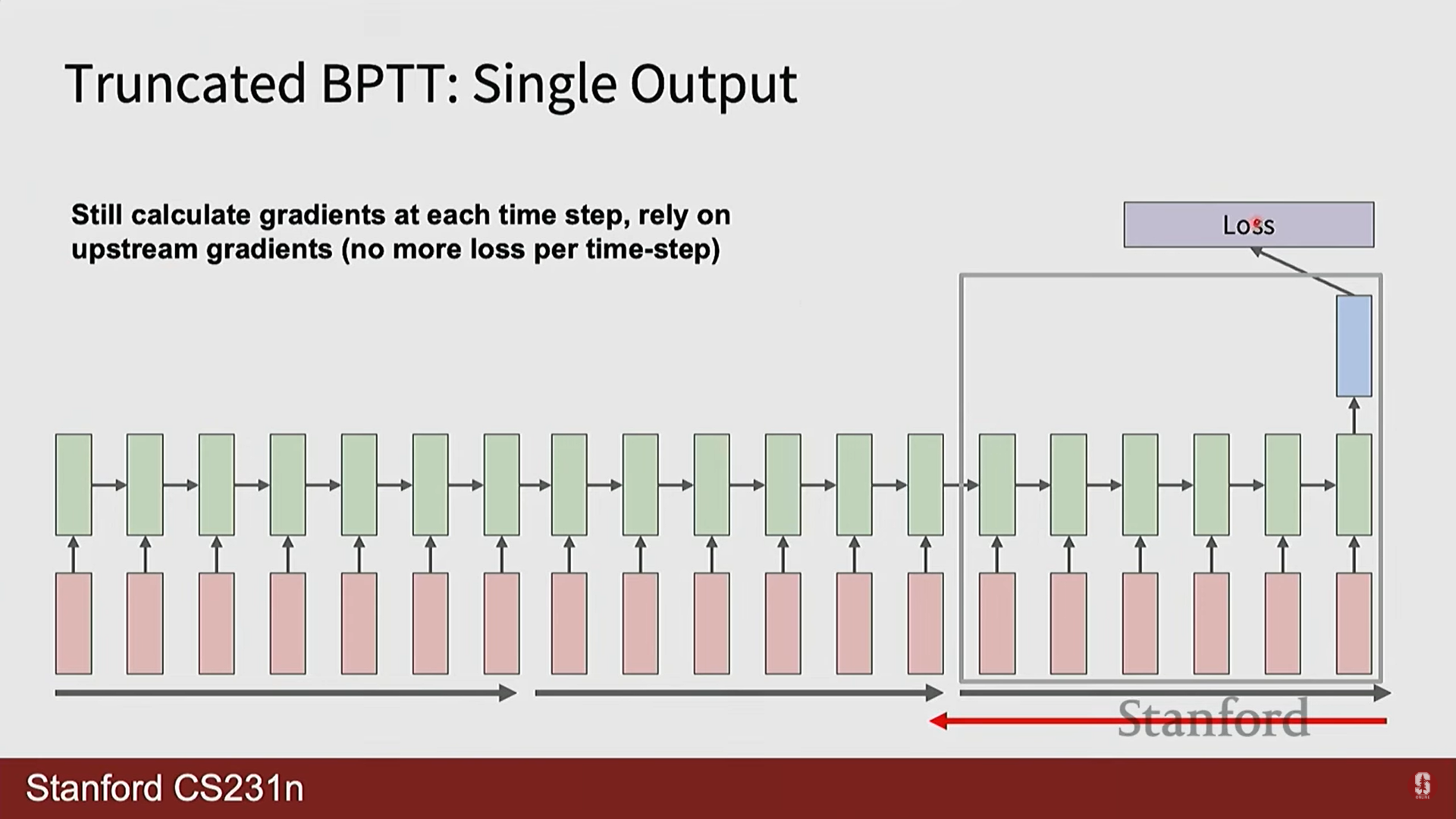
- 잘린 BPTT (Truncated BPTT): 매우 긴 시퀀스의 경우, 전체 길이에 대해 BPTT를 수행하면 GPU 메모리가 부족해질 수 있습니다. 이를 해결하기 위해 시퀀스를 일정한 길이의 청크(chunk)로 나누고, 각 청크 내에서만 역전파를 수행하는 실용적인 기법을 사용합니다.
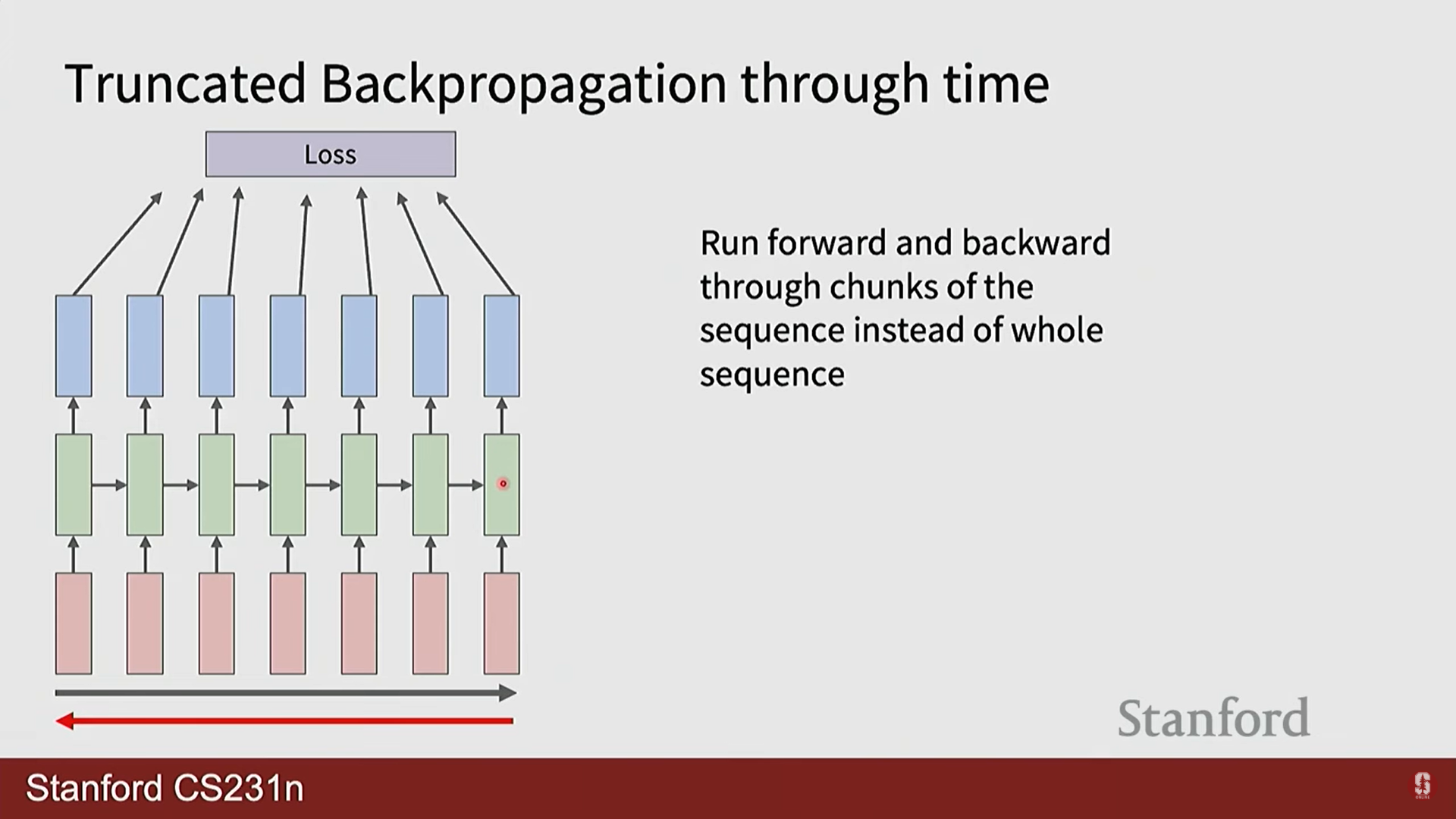
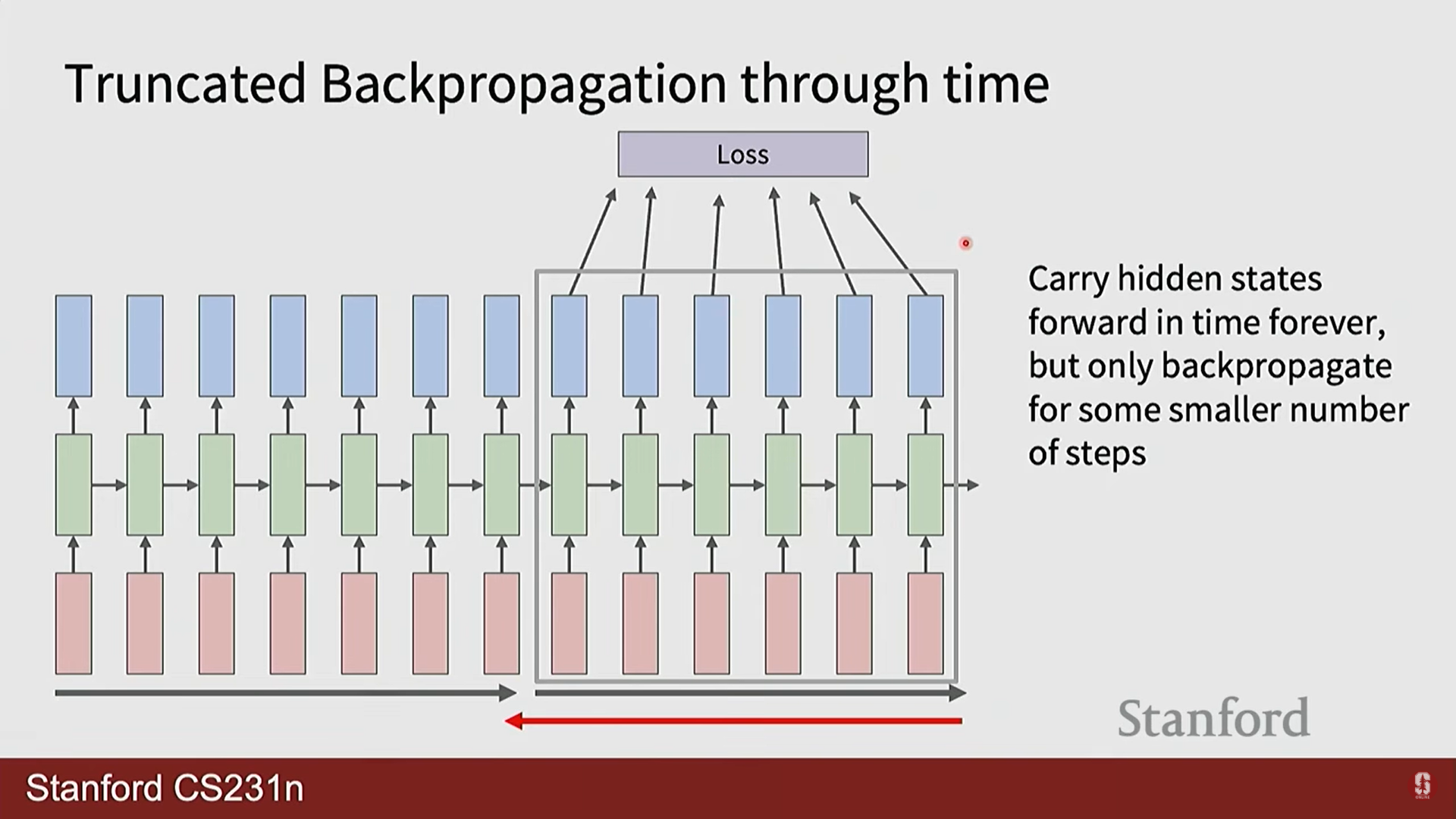
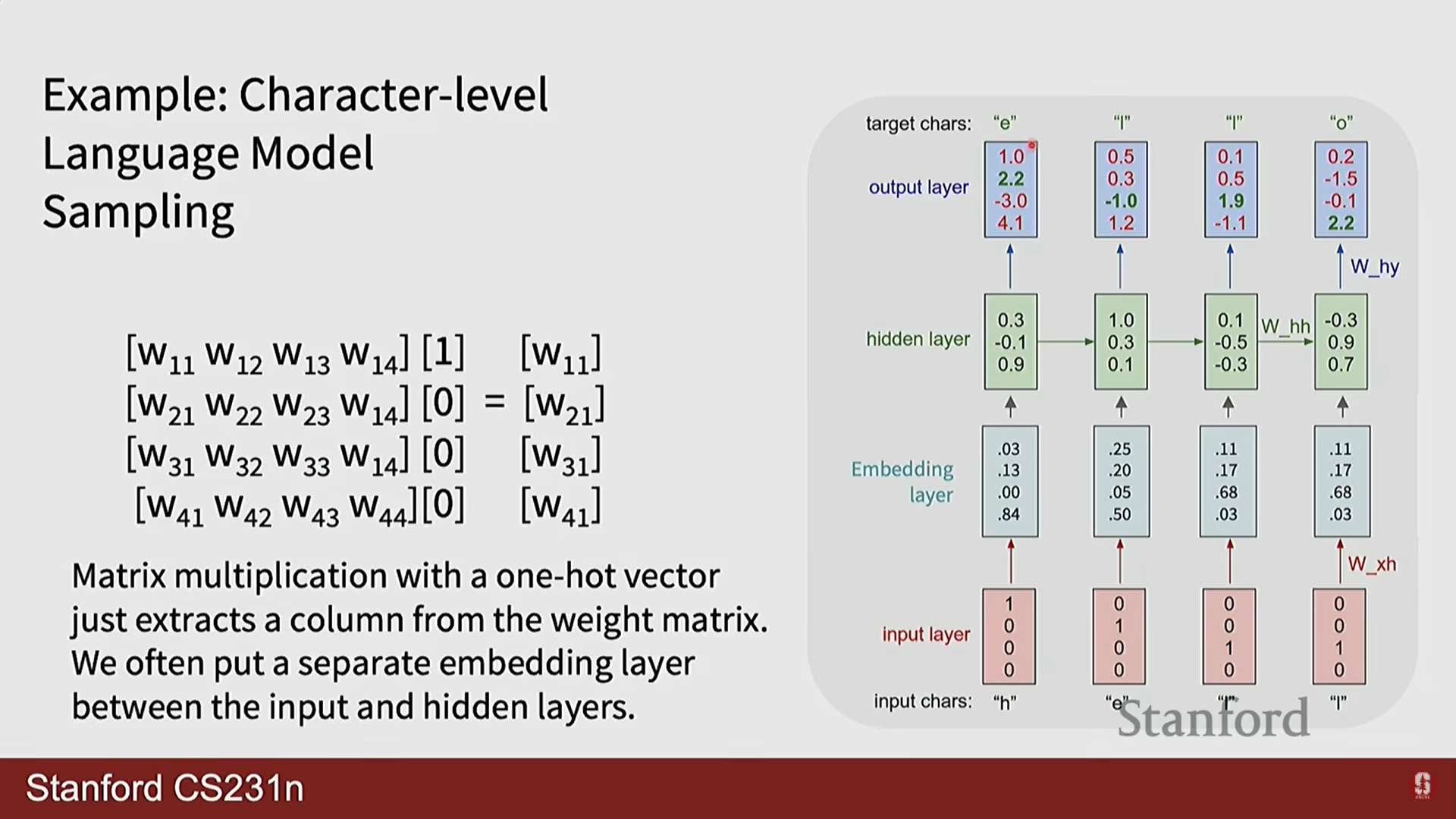
2) 문자 수준 언어 모델 (Character-level Language Model)
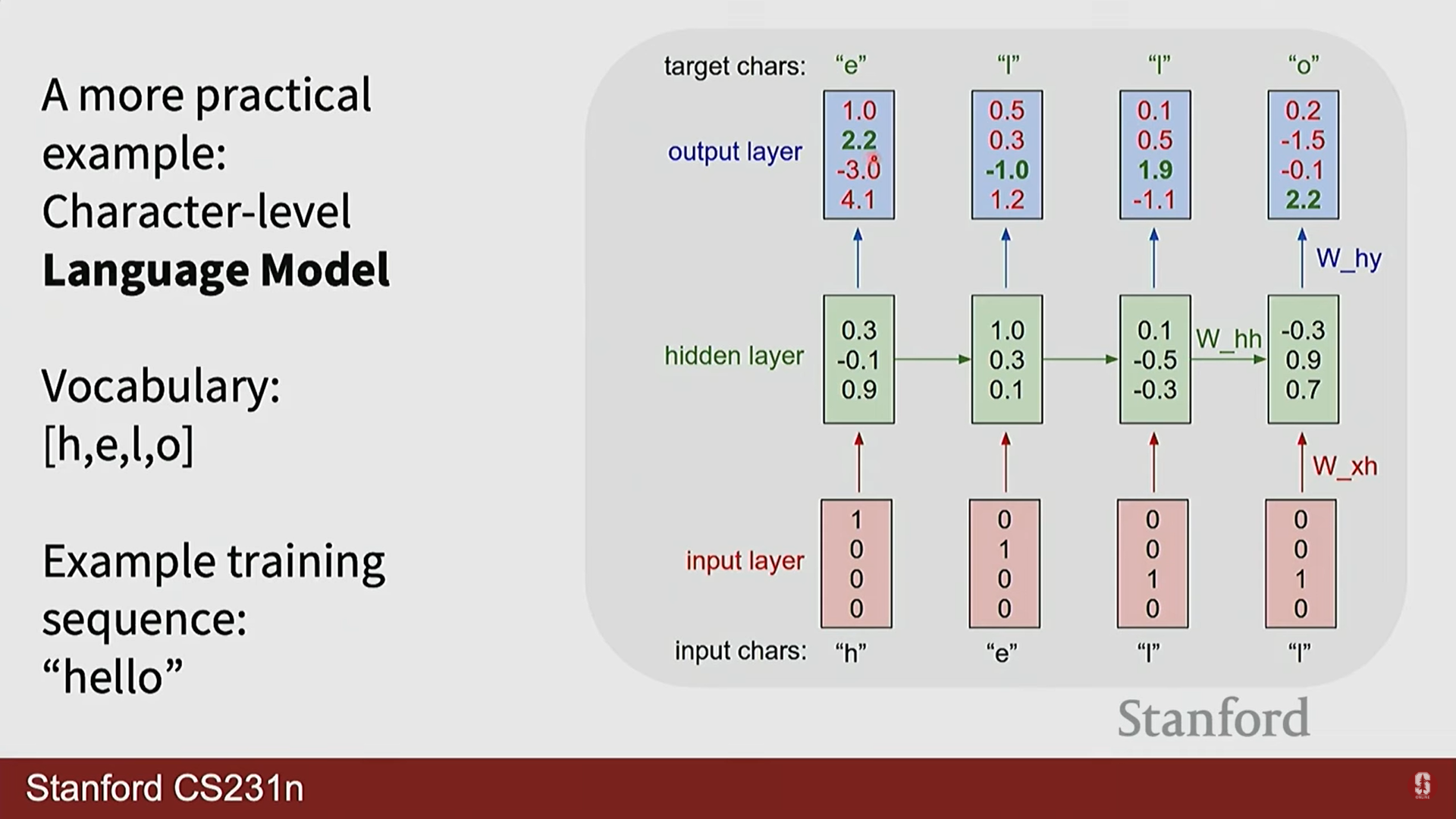
- RNN의 대표적인 응용 사례는 언어 모델링입니다. 이는 주어진 문자(또는 단어) 시퀀스를 바탕으로 다음에 나타날 문자를 예측하는 과제입니다.
- 작동 방식:
- 문자를 임베딩 벡터로 변환하여 입력합니다.
- RNN은 이전 문자들의 문맥을 은닉 상태 에 저장합니다.
- 은닉 상태를 출력 가중치 와 곱한 로짓(logit) 값에 소프트맥스(Softmax) 함수를 적용하여 다음 문자에 대한 확률 분포를 계산합니다.
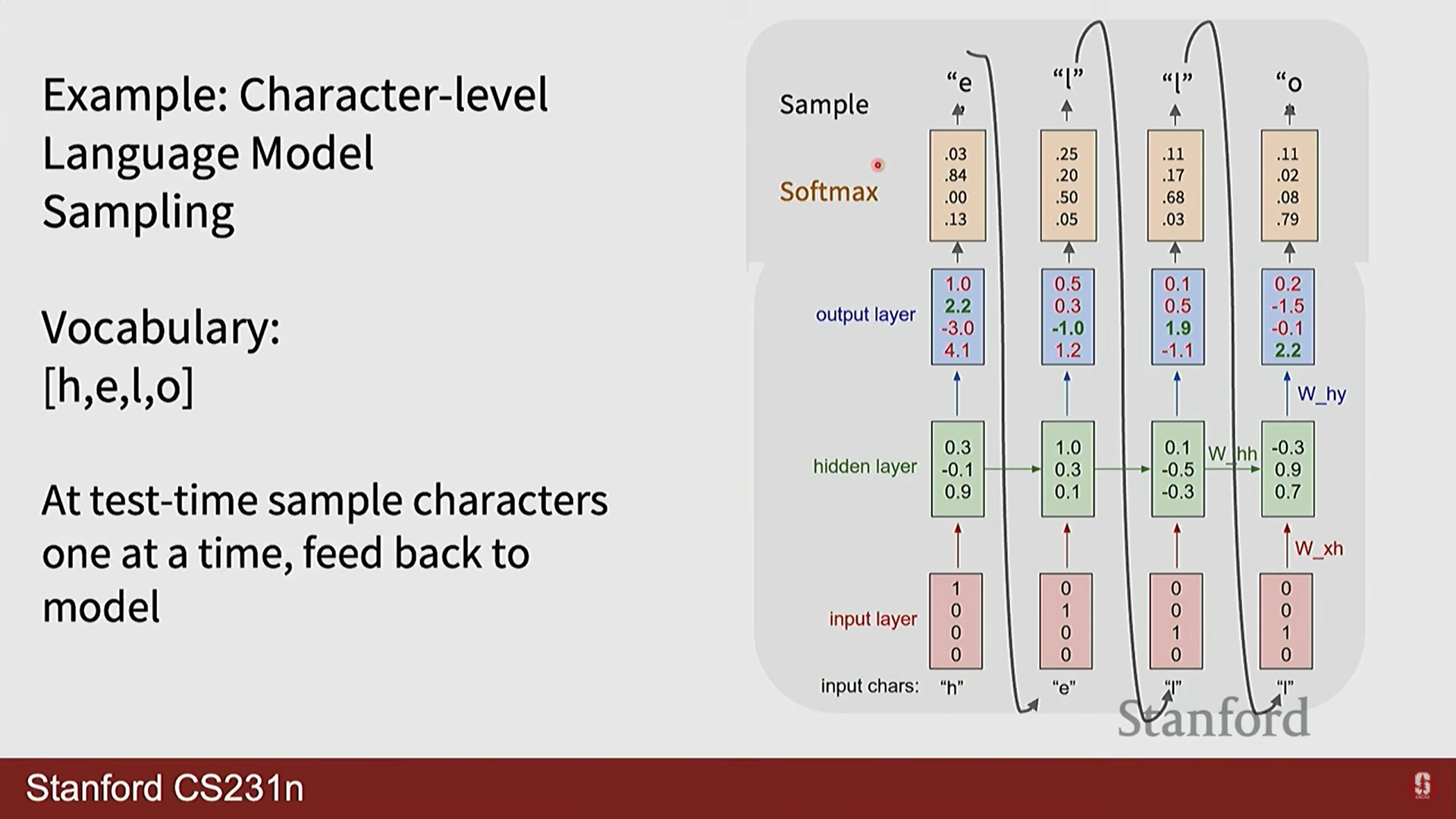
여기서 는 전체 어휘(vocabulary)의 크기입니다. - 테스트 시에는 이 확률 분포에서 다음 문자를 샘플링하여 생성하고, 이 생성된 문자를 다시 다음 시점의 입력으로 사용하는 자기회귀(Auto-regressive) 방식을 사용합니다.
부연설명
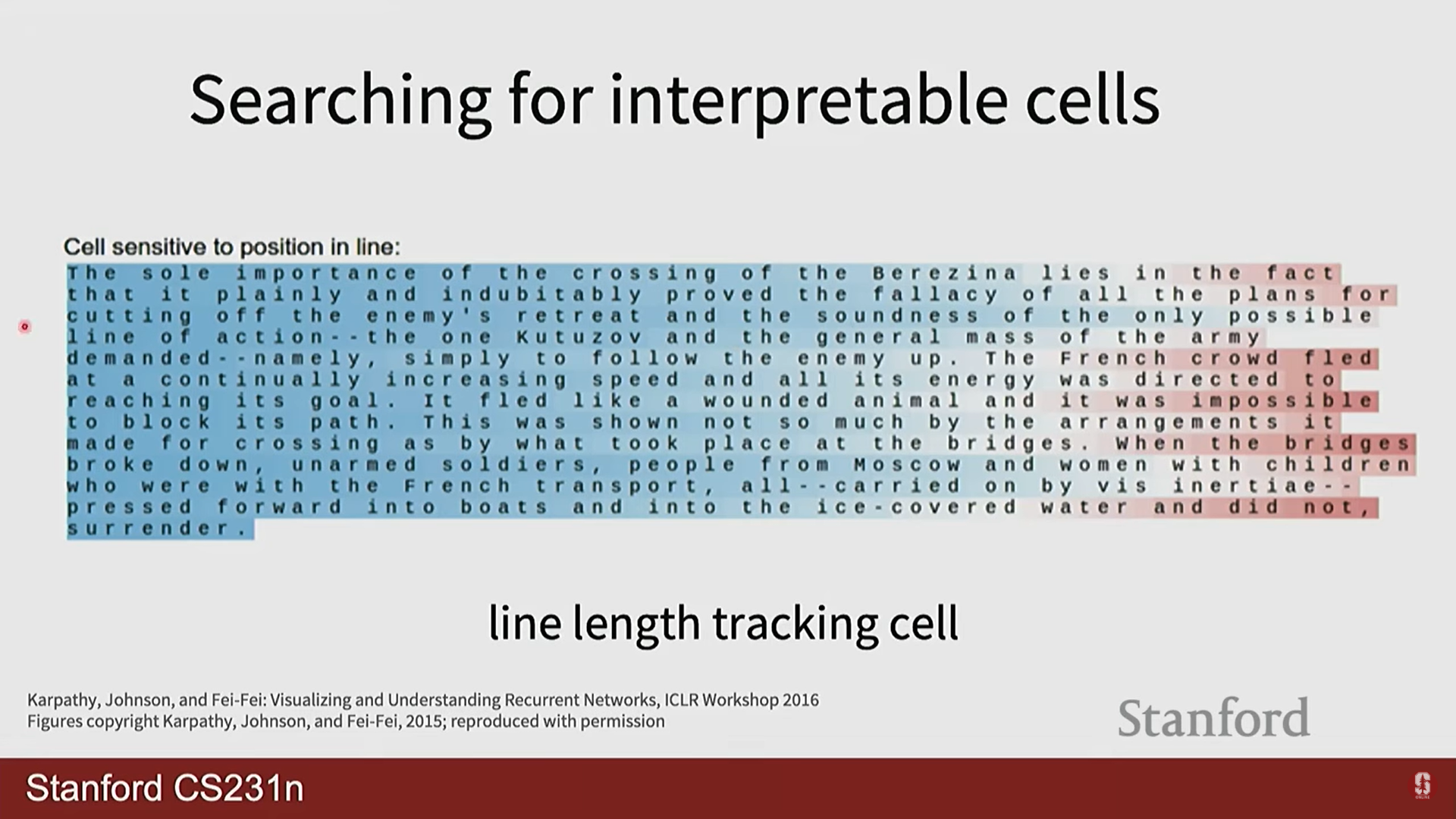
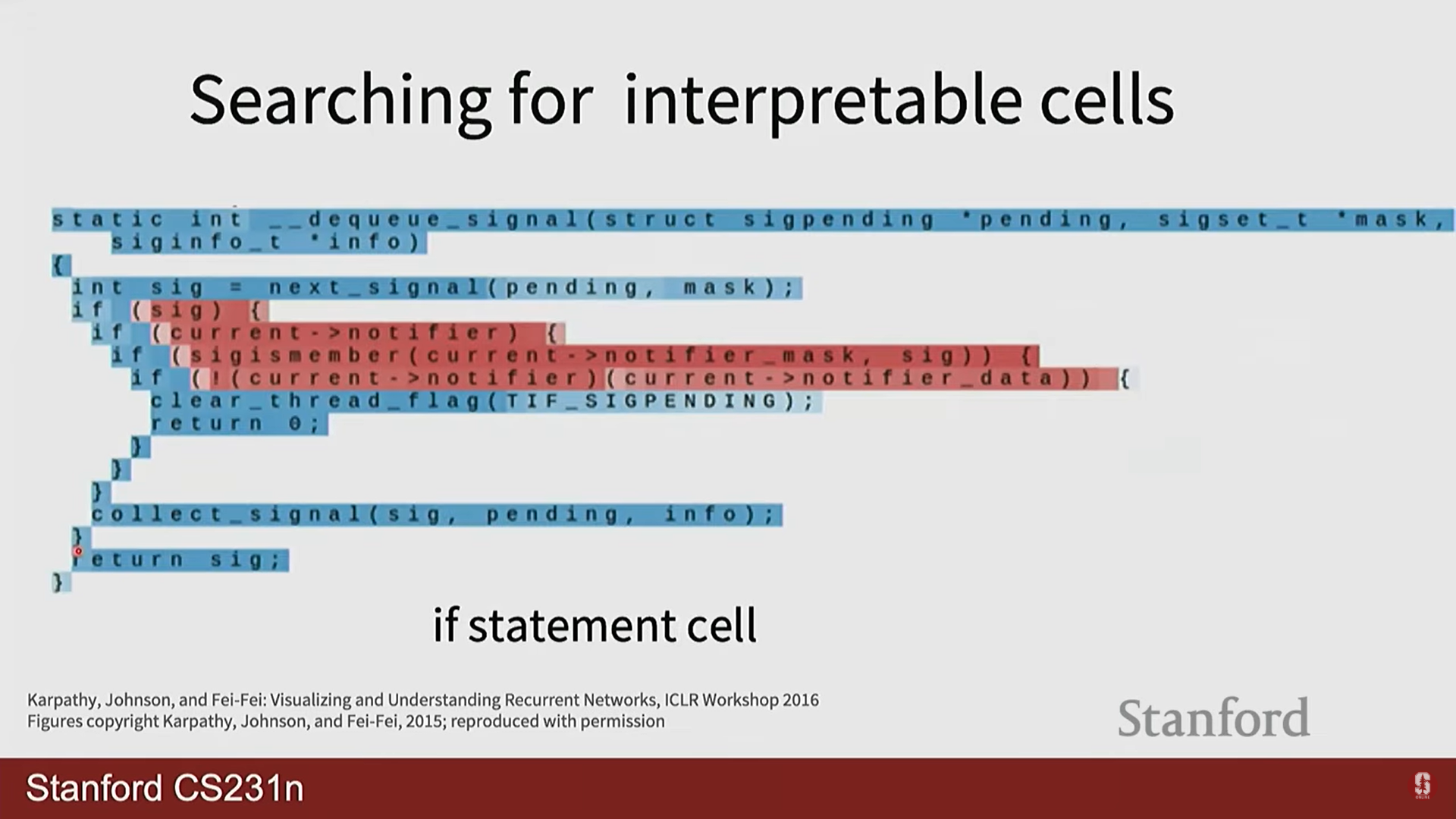
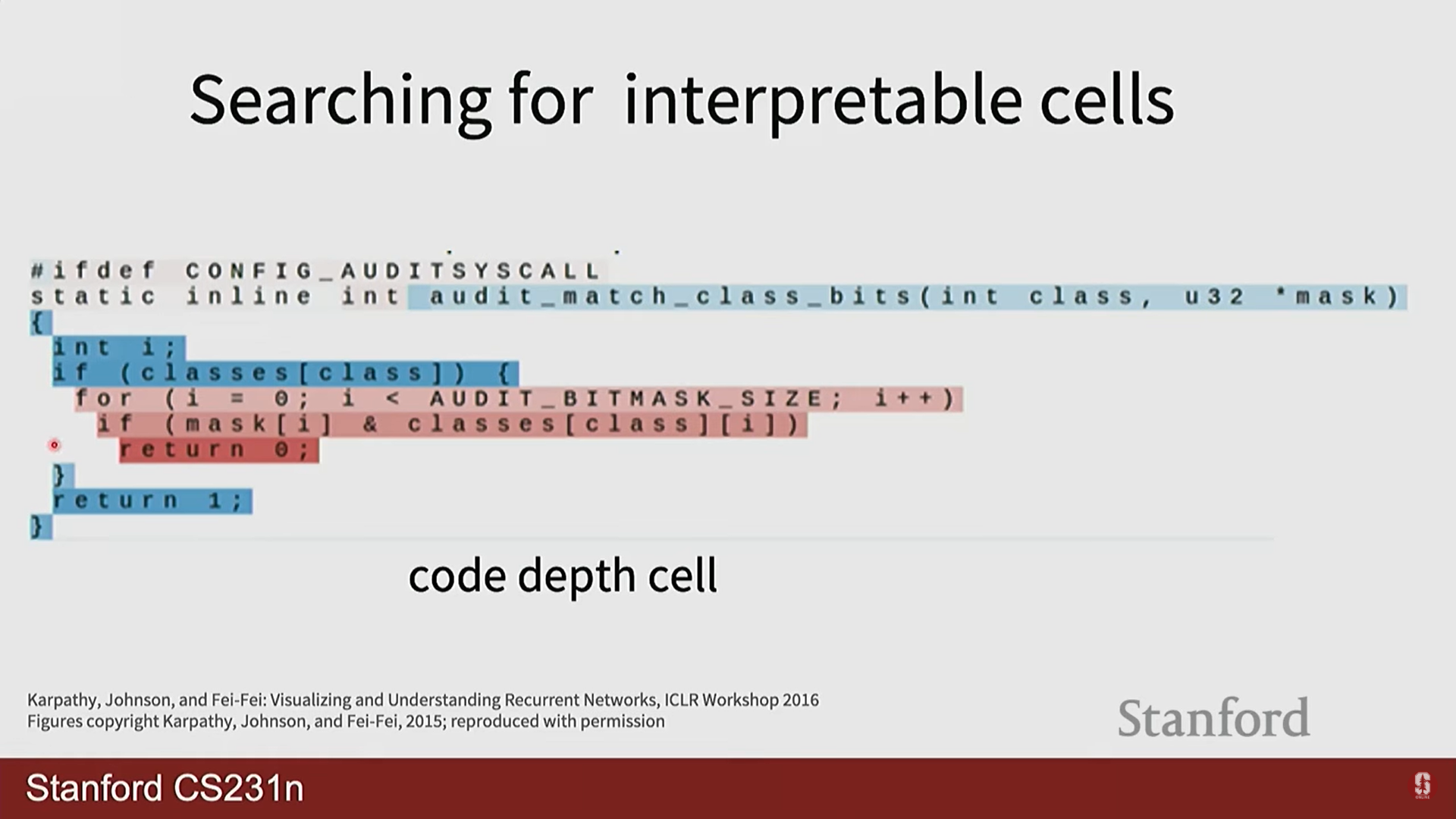
- Andrej Karpathy의 블로그 글 'The Unreasonable Effectiveness of Recurrent Neural Networks'에는 놀라운 예시들이 많습니다. 셰익스피어 텍스트로 학습시키면 셰익스피어 풍의 글을 생성하고, C언어 코드로 학습시키면 그럴듯한 C 코드를 만들어냅니다. 심지어 괄호를 열고 닫는 것, 들여쓰기 같은 복잡한 구조까지 학습하는 것을 볼 수 있습니다. 이는 RNN의 은닉 상태가 문맥 정보를 얼마나 잘 포착하는지 보여주는 좋은 예시입니다.
Searching for interpretable cells


3. RNN의 한계와 극복


1) 장기 의존성 문제 (Long-Term Dependency Problem)
-
RNN의 구조는 이론적으로는 먼 과거의 정보까지 활용할 수 있지만, 실제로는 기울기 소실/폭주(Vanishing/Exploding Gradients) 문제 때문에 장기 의존성을 학습하기 매우 어렵습니다.
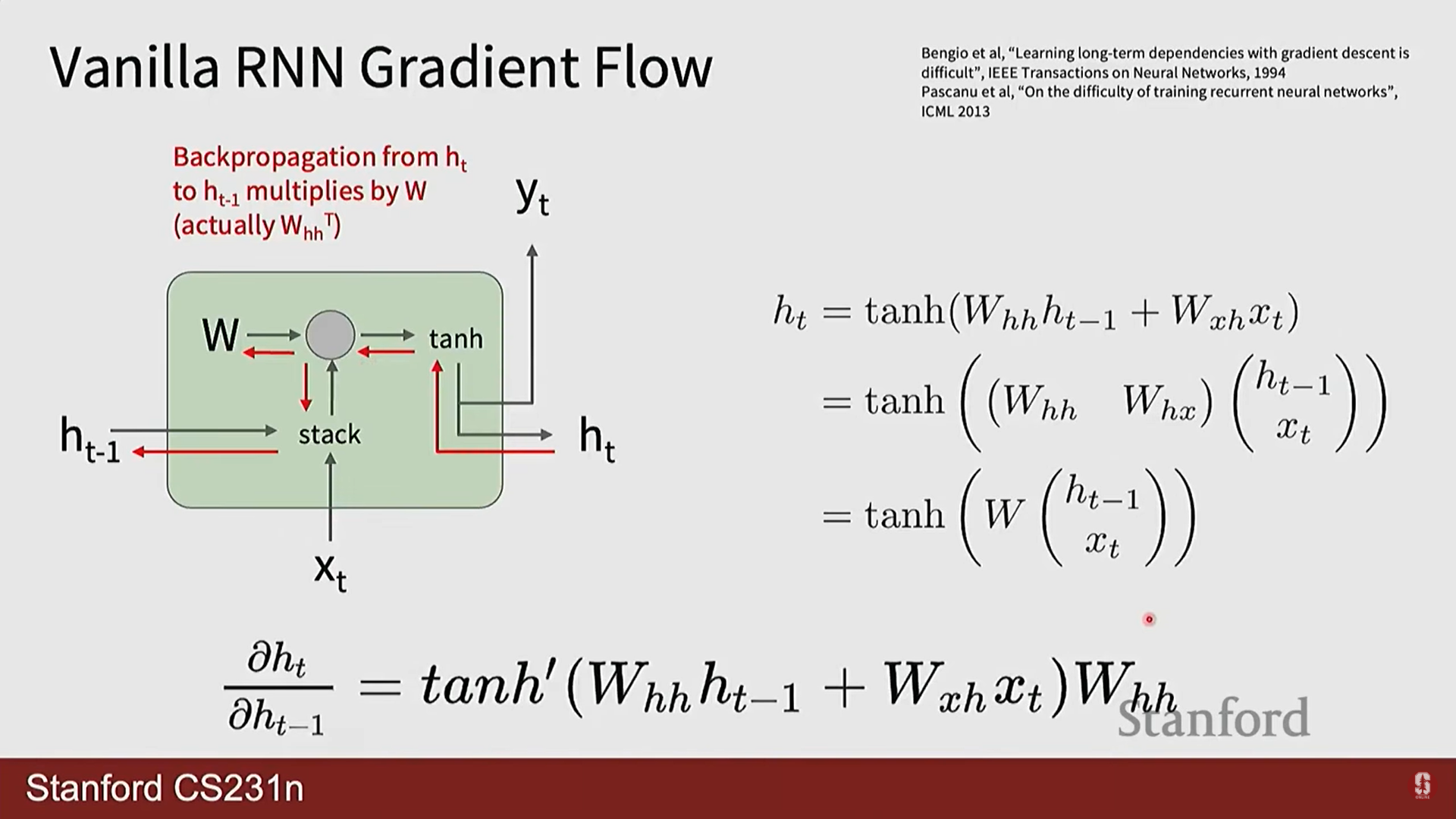
-
기울기 계산의 본질: BPTT 과정에서 먼 과거의 은닉 상태 가 현재의 손실 에 미치는 영향을 계산하려면 연쇄 법칙(chain rule)에 따라 여러 자코비안 행렬을 곱해야 합니다.
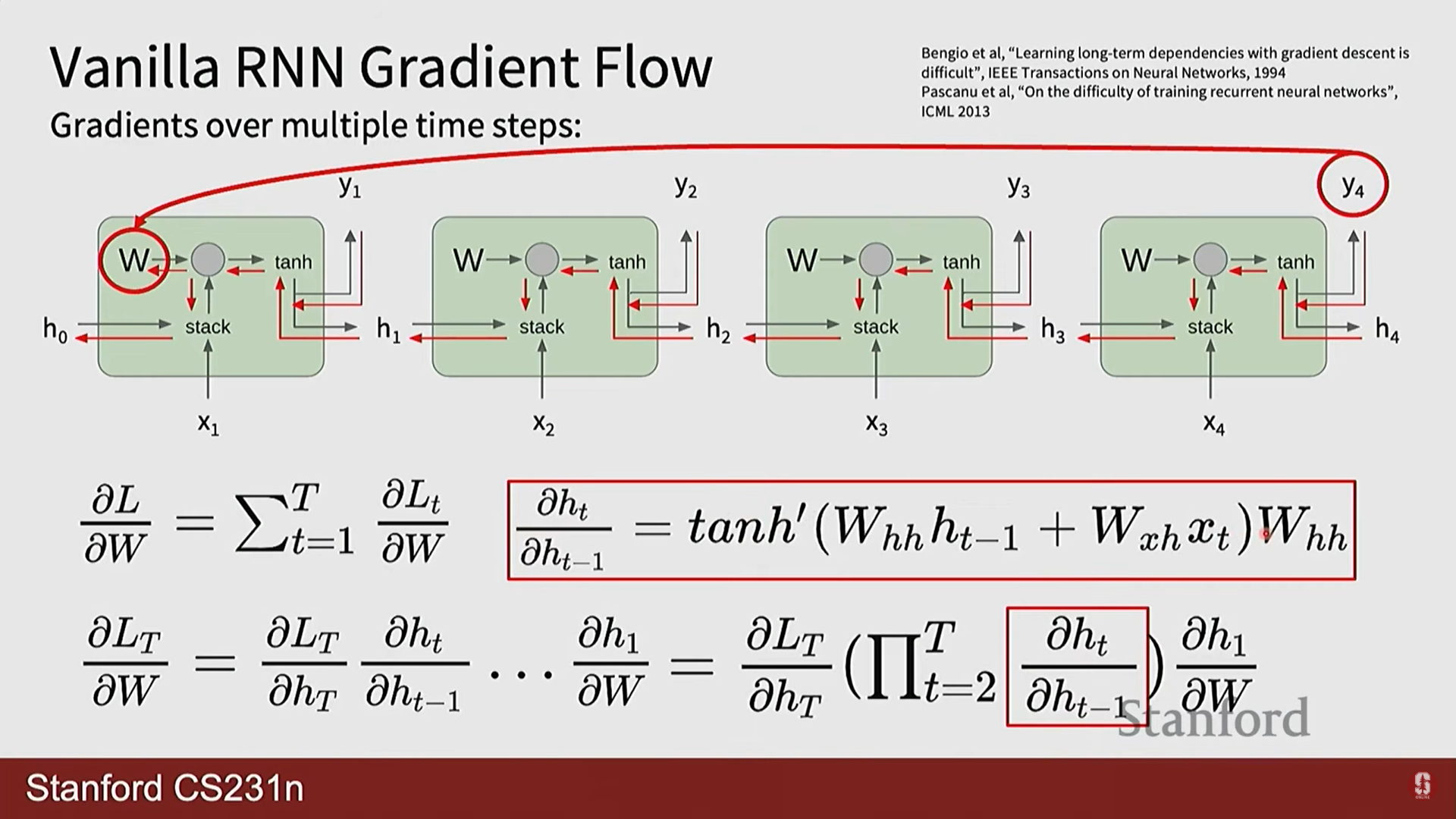
여기서 각 자코비안 행렬은 입니다. -
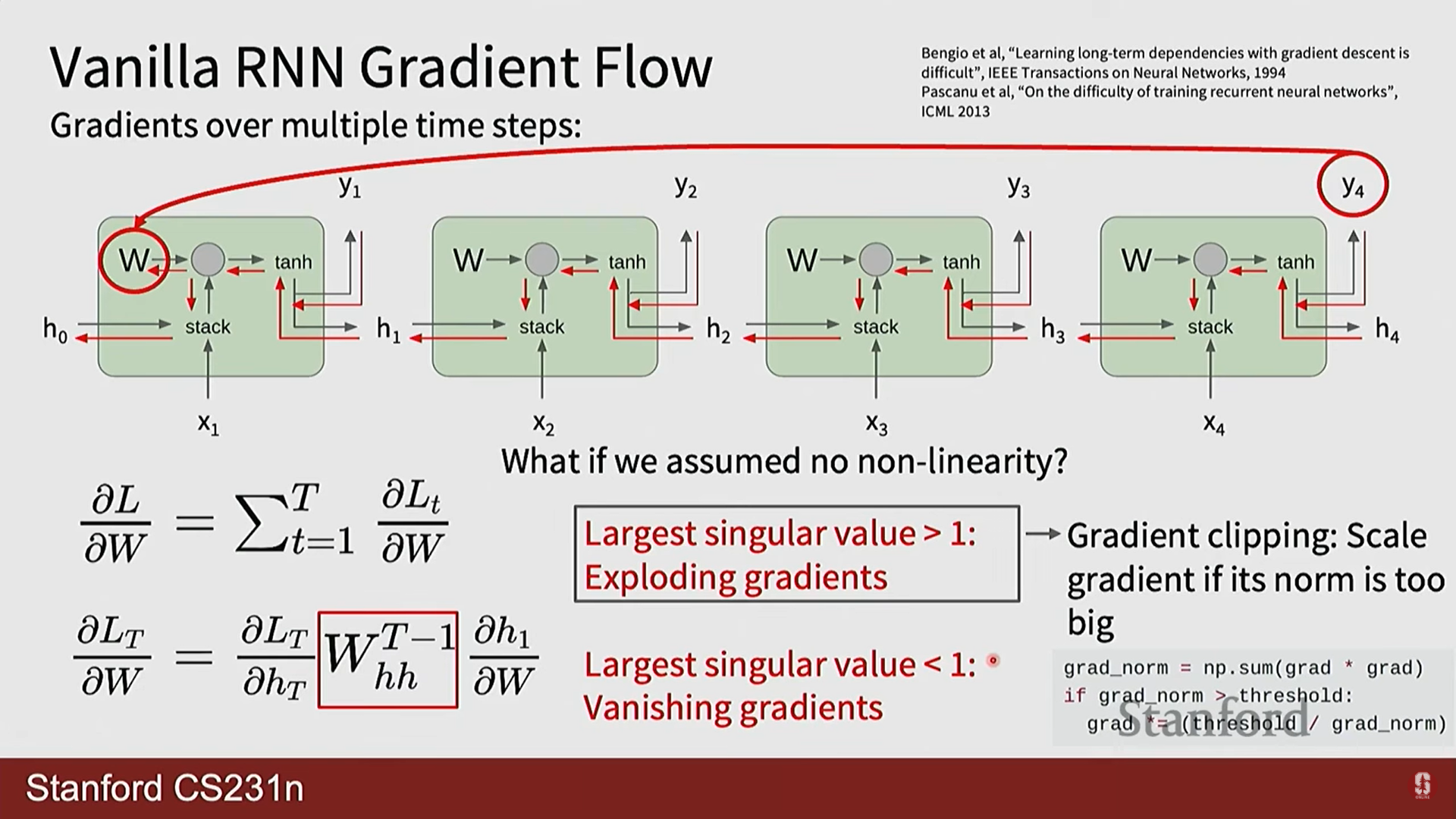
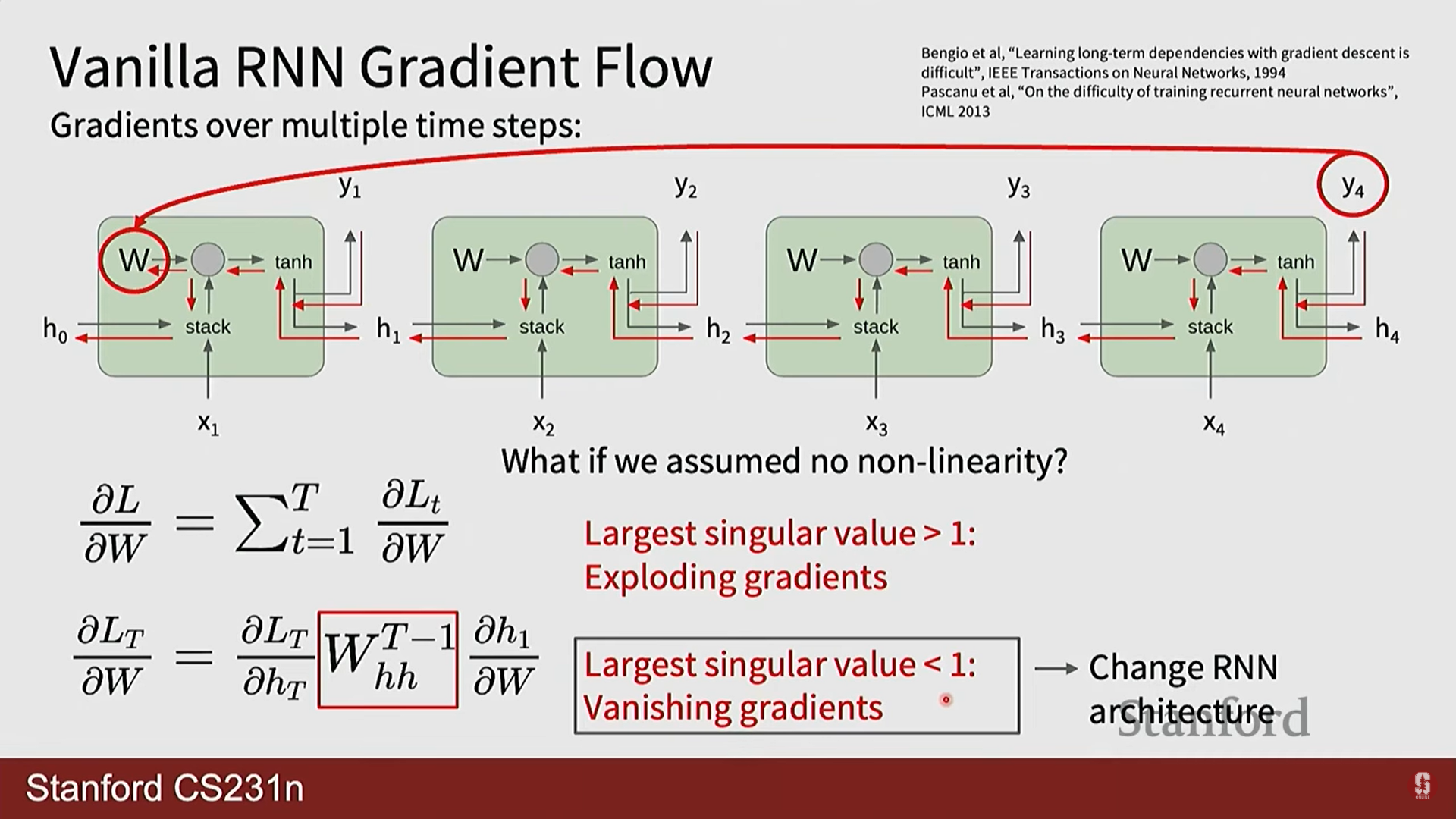
기울기 소실 및 폭주: 위 식에서 보듯이, 가중치 행렬 가 반복적으로 곱해지게 됩니다.
- 폭주(Exploding): 의 가장 큰 특이값(singular value)이 1보다 크면, 이 행렬이 반복적으로 곱해질 때 기울기가 지수적으로 발산합니다. 이는 기울기 클리핑(Gradient Clipping)으로 비교적 쉽게 해결 가능합니다.
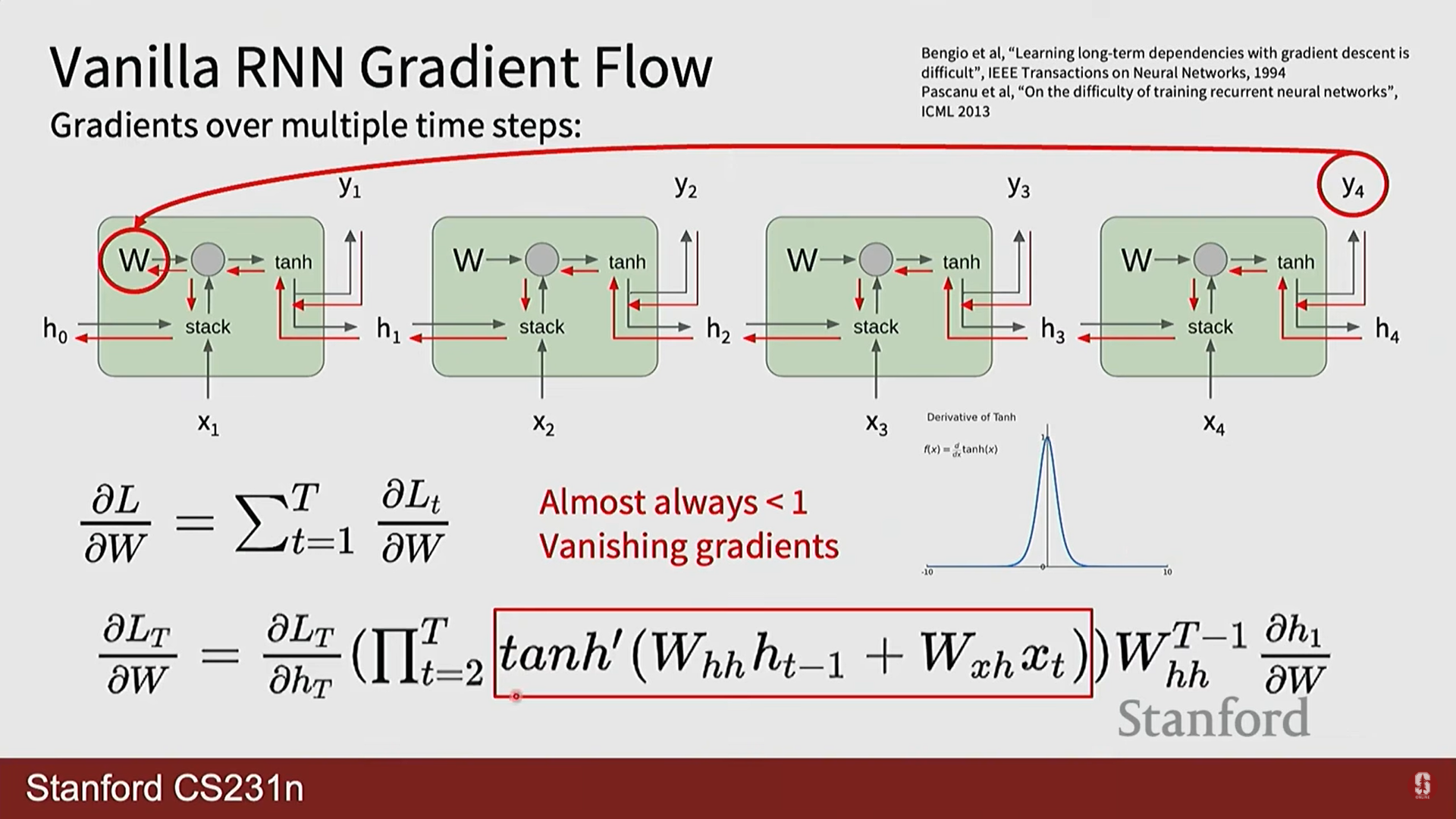
- 소실(Vanishing): 반대로 의 가장 큰 특이값이 1보다 작으면, 기울기가 지수적으로 0에 수렴하여 사라집니다. 이는 훨씬 더 심각하고 해결하기 어려운 문제로, 시퀀스 초반의 정보가 학습에 거의 영향을 미치지 못하게 만듭니다.
2) LSTM (Long Short-Term Memory) - History Note
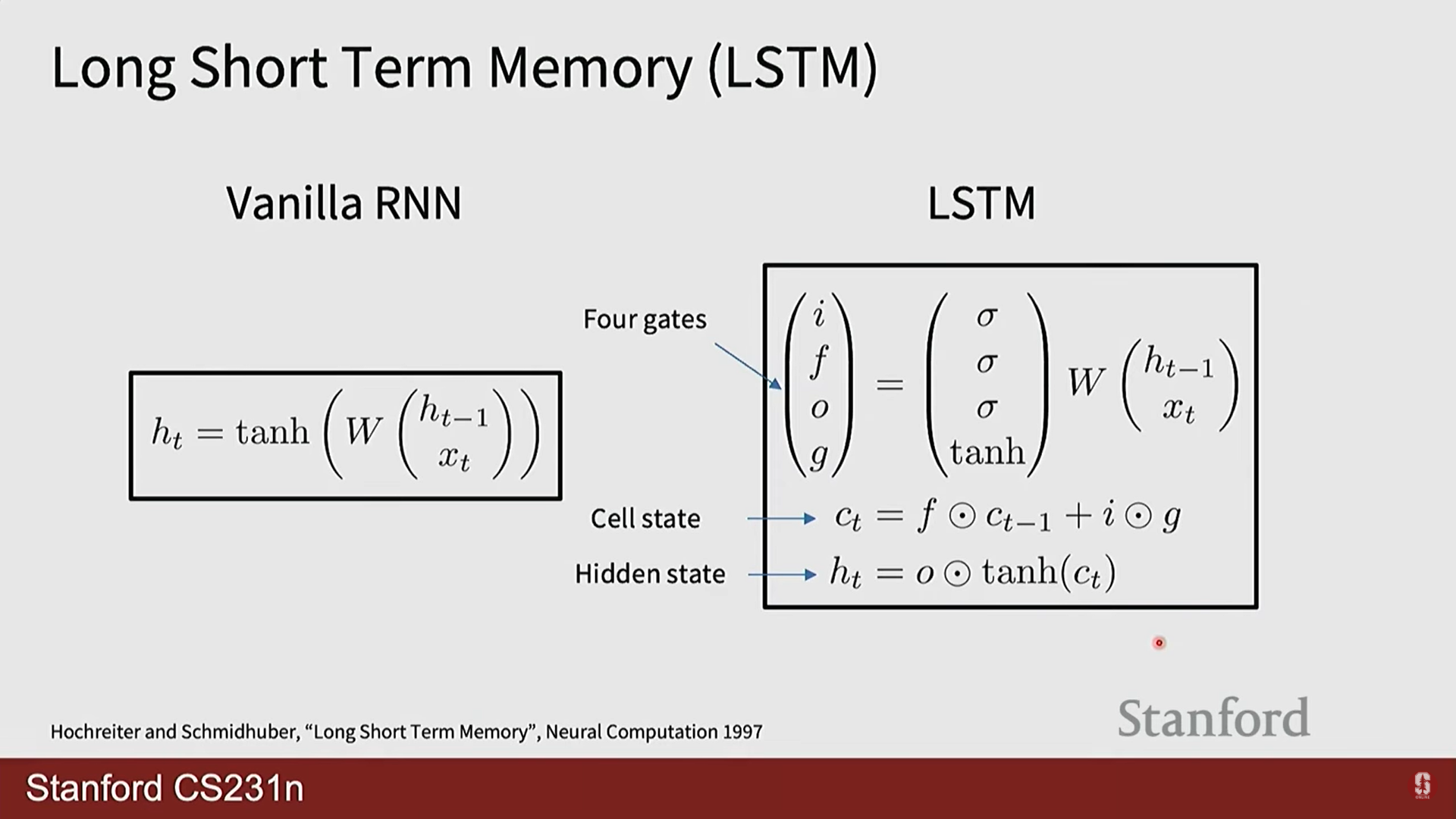
- LSTM은 바닐라 RNN의 치명적인 단점인 기울기 소실 문제를 해결하기 위해 고안된 매우 효과적인 변형 모델입니다.
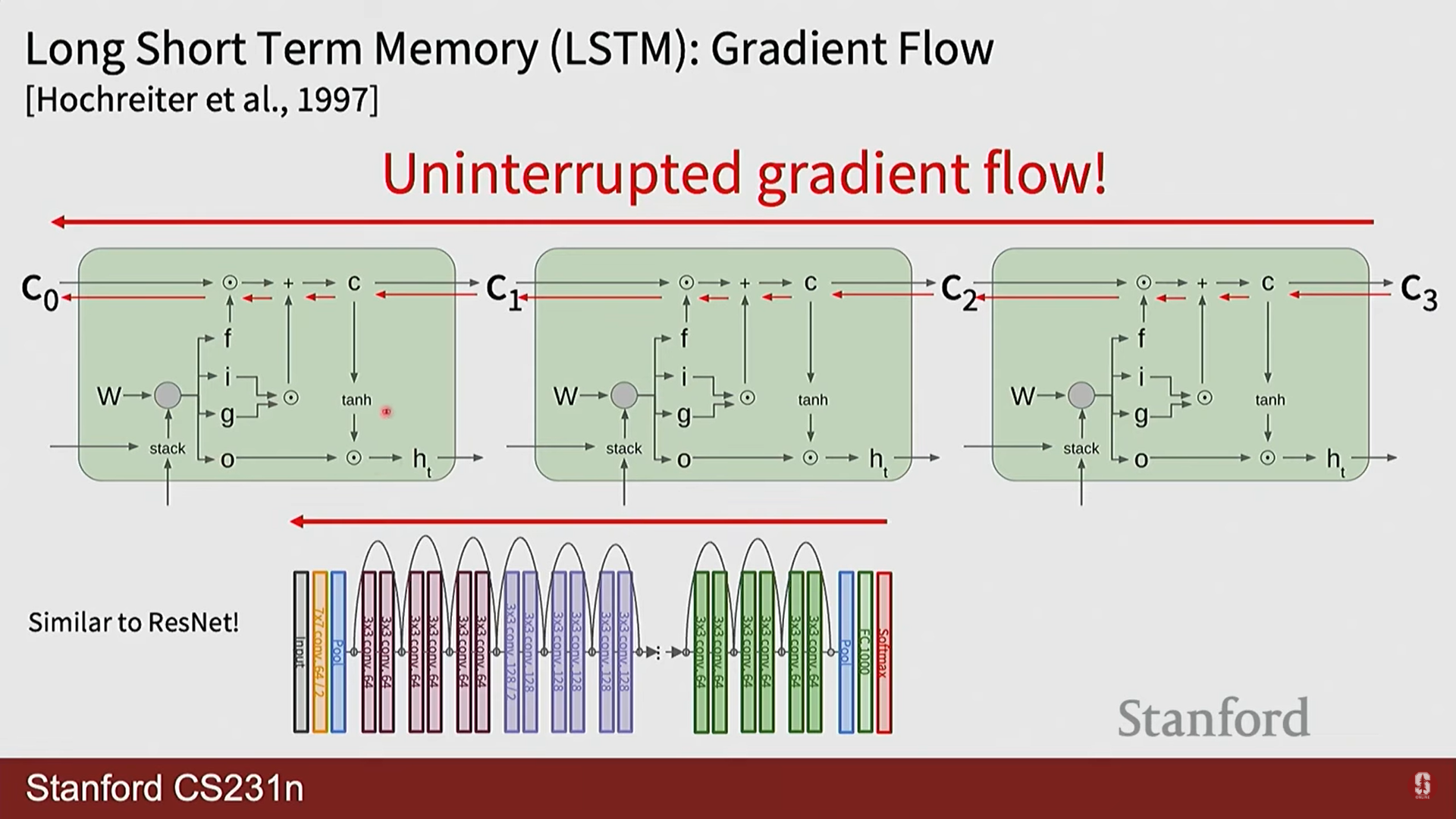
- 핵심 아이디어: 기존 은닉 상태() 외에, 정보의 장기 저장을 위한 별도의 셀 상태(cell state, )를 도입했습니다. 셀 상태는 정보가 거의 변형되지 않고 직접 흘러가는 일종의 '고속도로(highway)' 역할을 합니다.
- 게이트(Gate) 메커니즘의 수학적 표현:
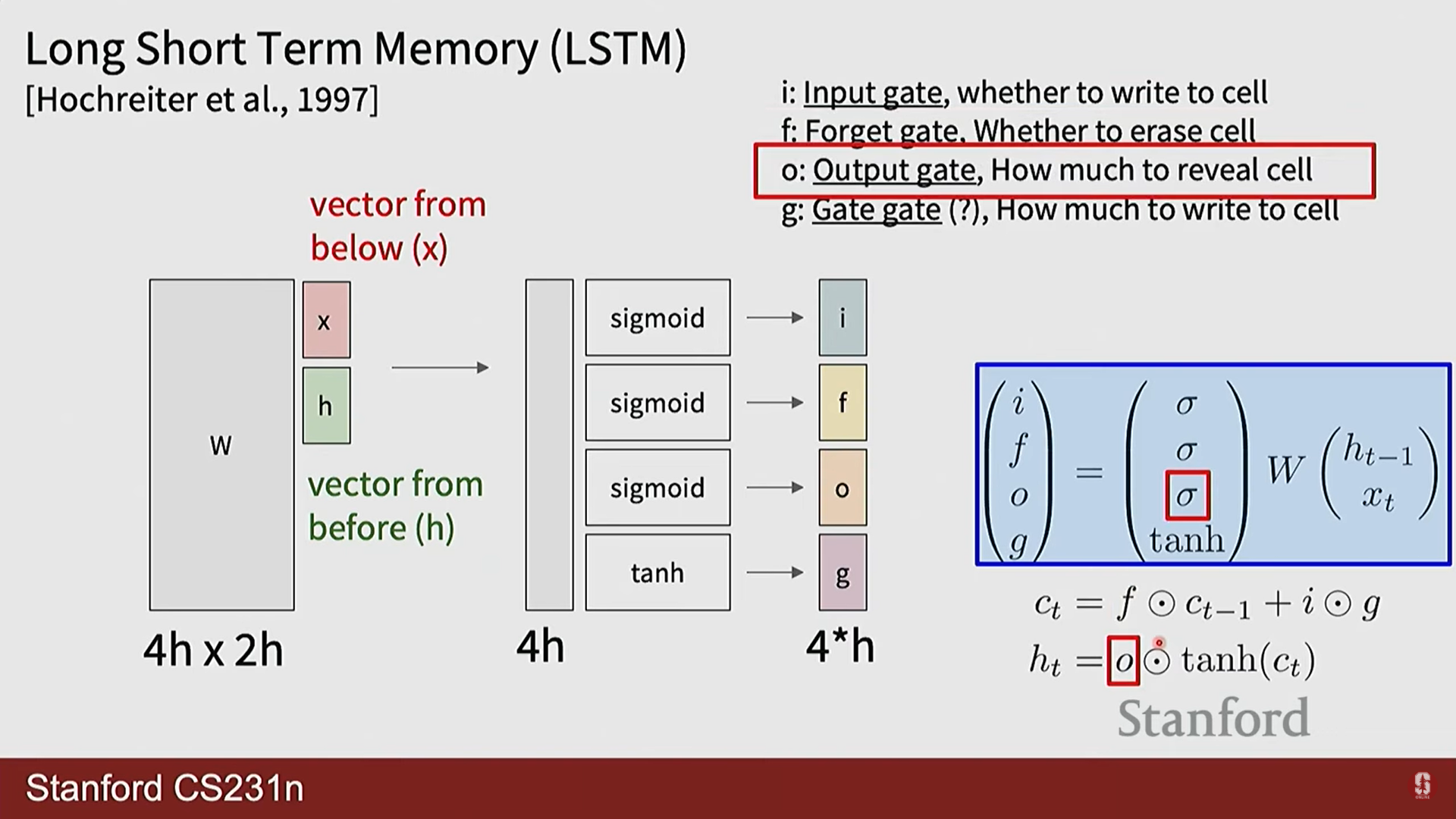
- 망각 게이트 (): 이전 셀 상태()의 정보를 얼마나 잊을지 결정합니다.
- 입력 게이트 (): 새로운 정보를 얼마나 셀 상태에 반영할지 결정합니다.
- 게이트 게이트 (): 셀 상태에 추가할 후보 정보를 생성합니다.
- 셀 상태 업데이트:
- 출력 게이트 (): 셀 상태의 정보를 얼마나 외부(은닉 상태)로 보낼지 결정합니다.
여기서 는 시그모이드 함수, 는 요소별 곱셈(element-wise product)을 의미합니다.
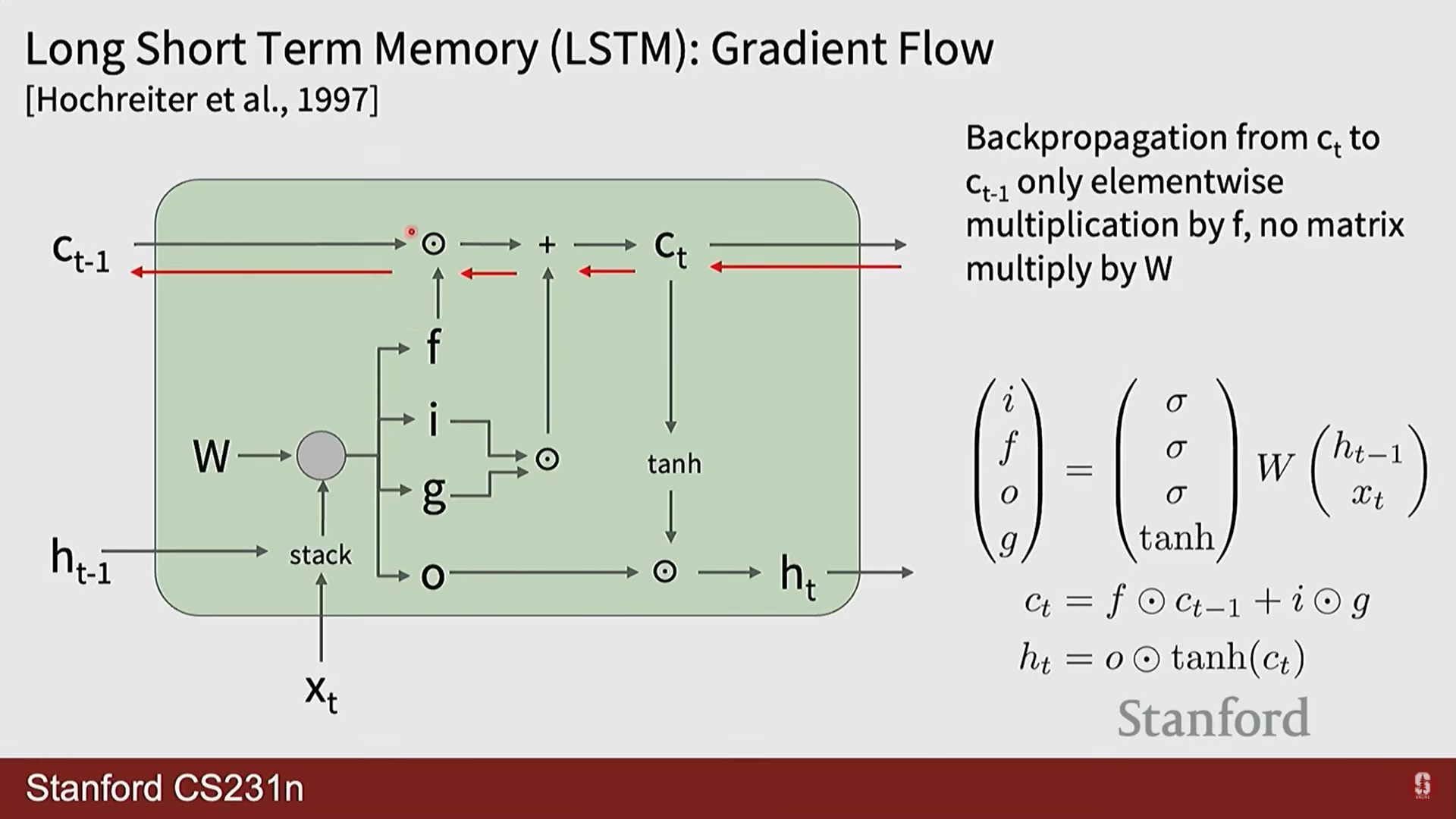
- 망각 게이트 (): 이전 셀 상태()의 정보를 얼마나 잊을지 결정합니다.
부연설명
- LSTM의 작동 방식은 ResNet의 스킵 커넥션과 철학적으로 유사합니다. ResNet이 덧셈을 통해 정보가 레이어를 건너뛸 수 있는 경로를 만들어 깊은 네트워크의 학습을 용이하게 한 것처럼, LSTM은 셀 상태라는 경로를 통해 정보가 여러 시점을 건너뛸 수 있도록 하여 긴 시퀀스의 학습을 가능하게 합니다.
4. CV 분야에서의 RNN 응용과 최신 동향
1) 이미지 캡셔닝 및 시각적 질의응답 (VQA)
-
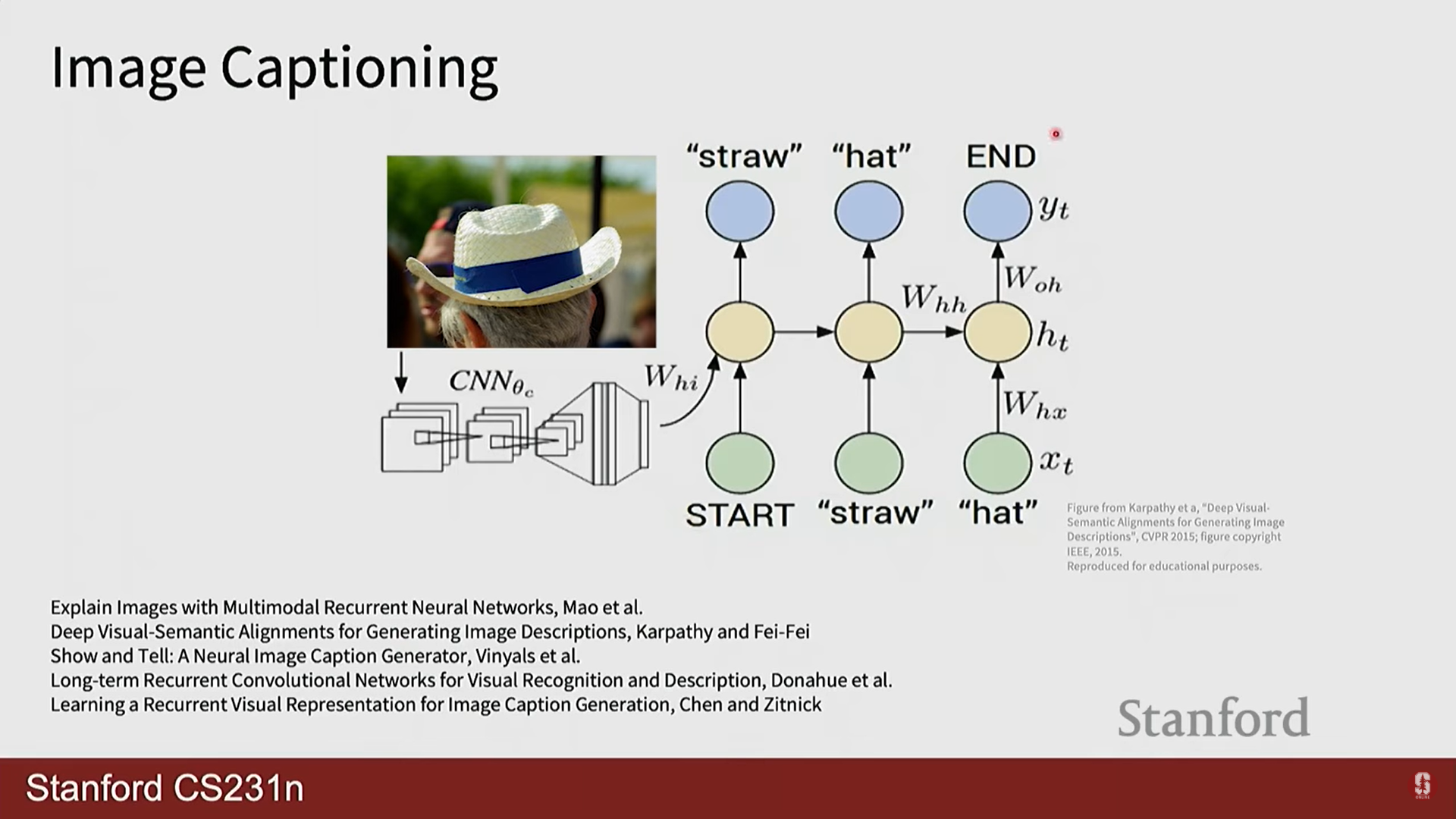
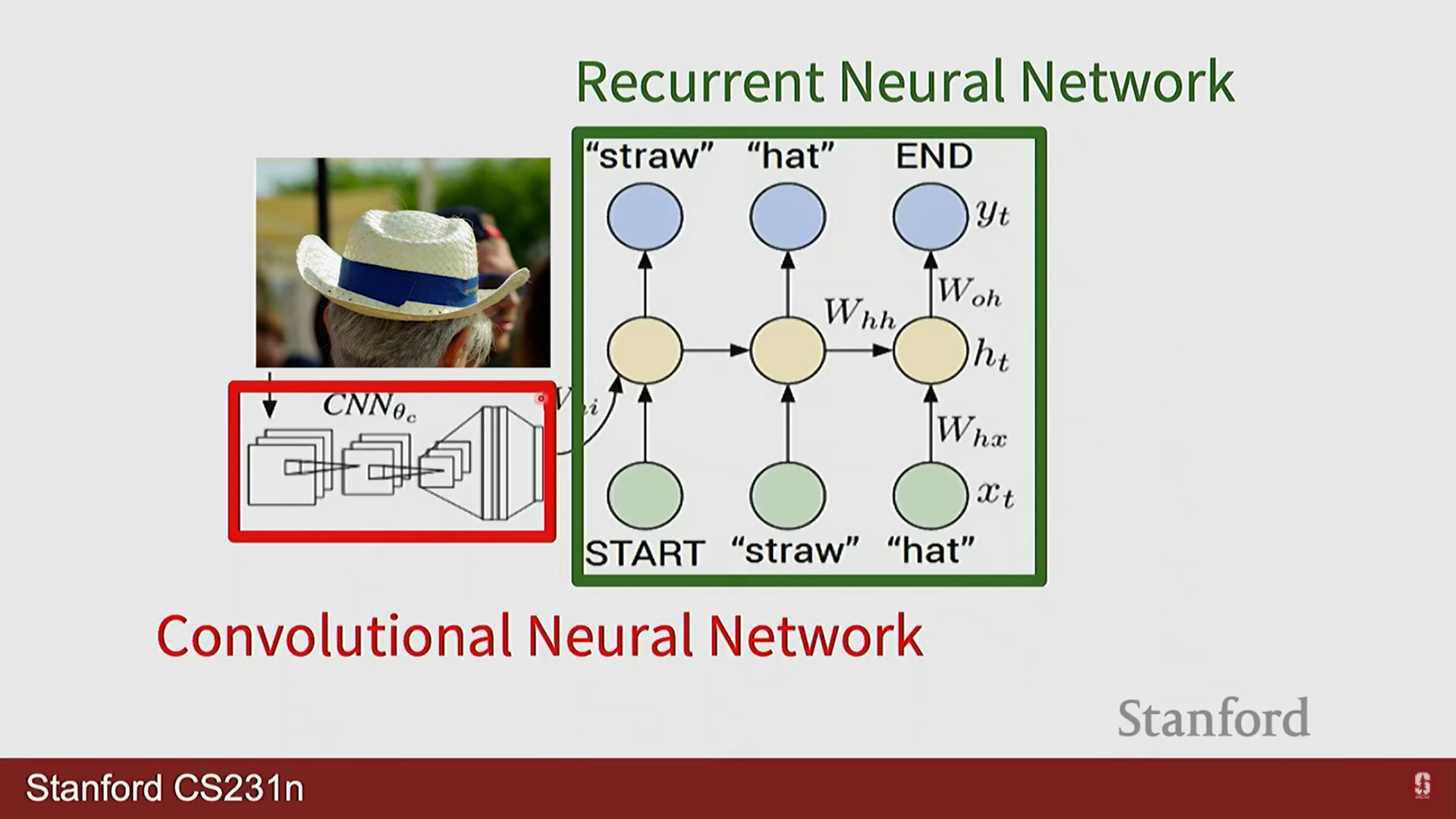
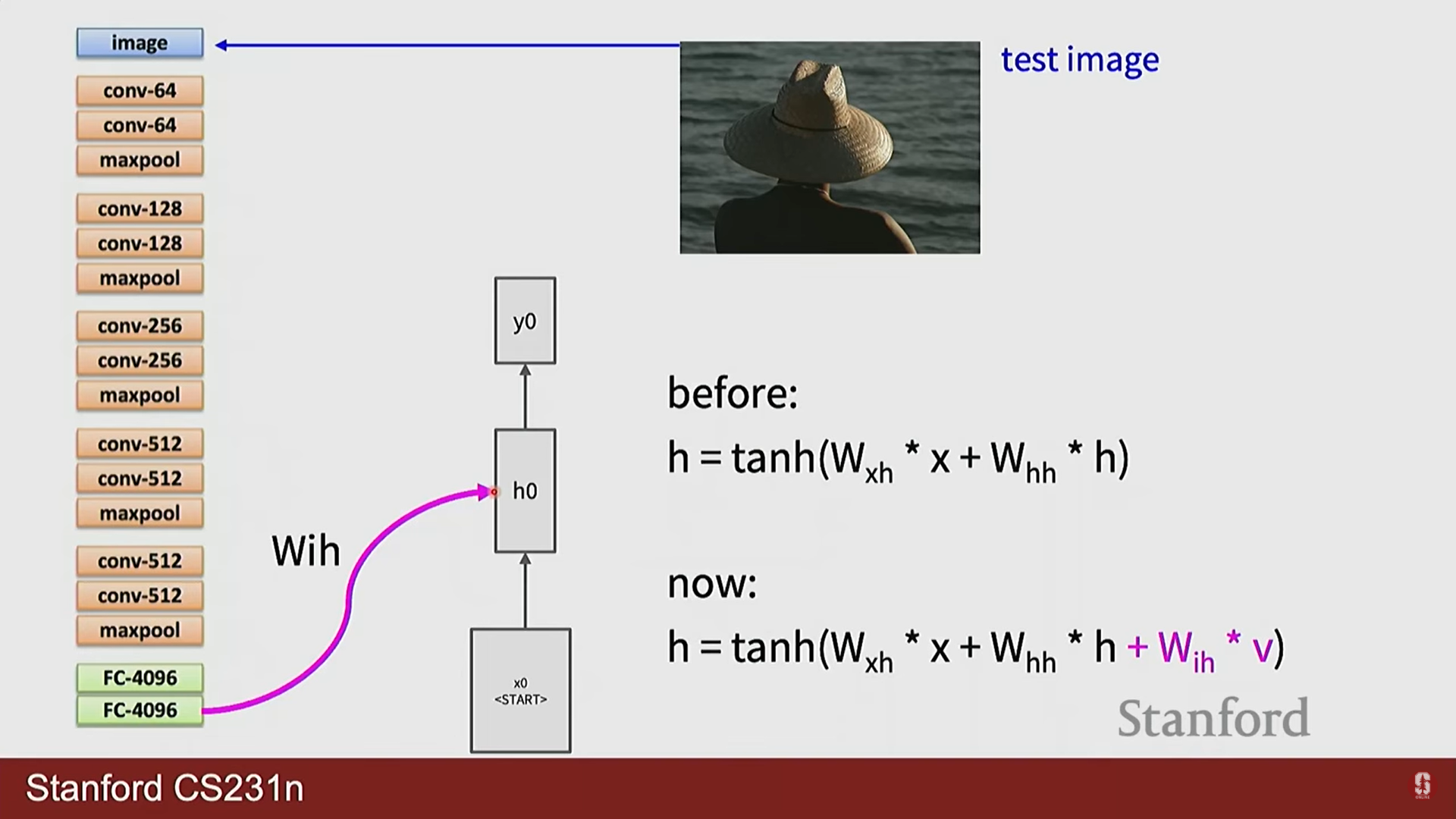
이미지 캡셔닝: CNN으로 이미지 특징을 추출하고, 이 특징 벡터를 RNN의 초기 상태로 입력하여 순차적으로 이미지 설명 문장을 생성하는 대표적인 CV+RNN 결합 모델입니다.
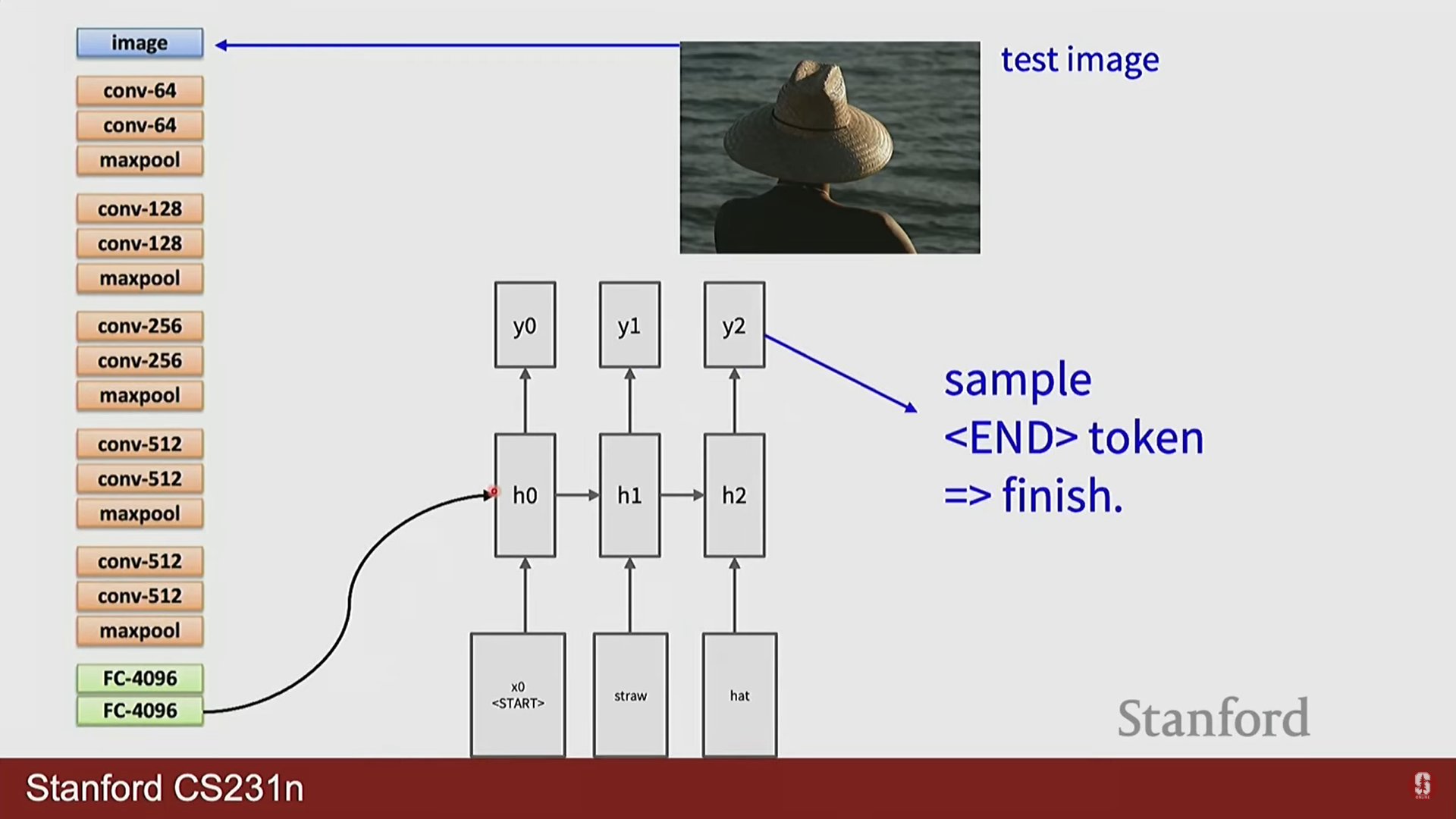


-
VQA: 이미지와 질문(문장 시퀀스)을 각각 CNN과 RNN으로 처리한 후, 두 정보를 융합하여 질문에 대한 답을 생성하는 과제입니다.

부연설명
- 이미지 캡셔닝 모델은 때때로 재미있는 실수를 합니다. 훈련 데이터에 없던 생소한 상황을 주면, 모델이 본 적 없는 물체를 '환각(hallucinate)'처럼 만들어내기도 합니다. 이는 모델이 훈련 데이터의 편향(bias)을 학습했기 때문이며, 모델의 한계를 명확히 보여주는 예시입니다.
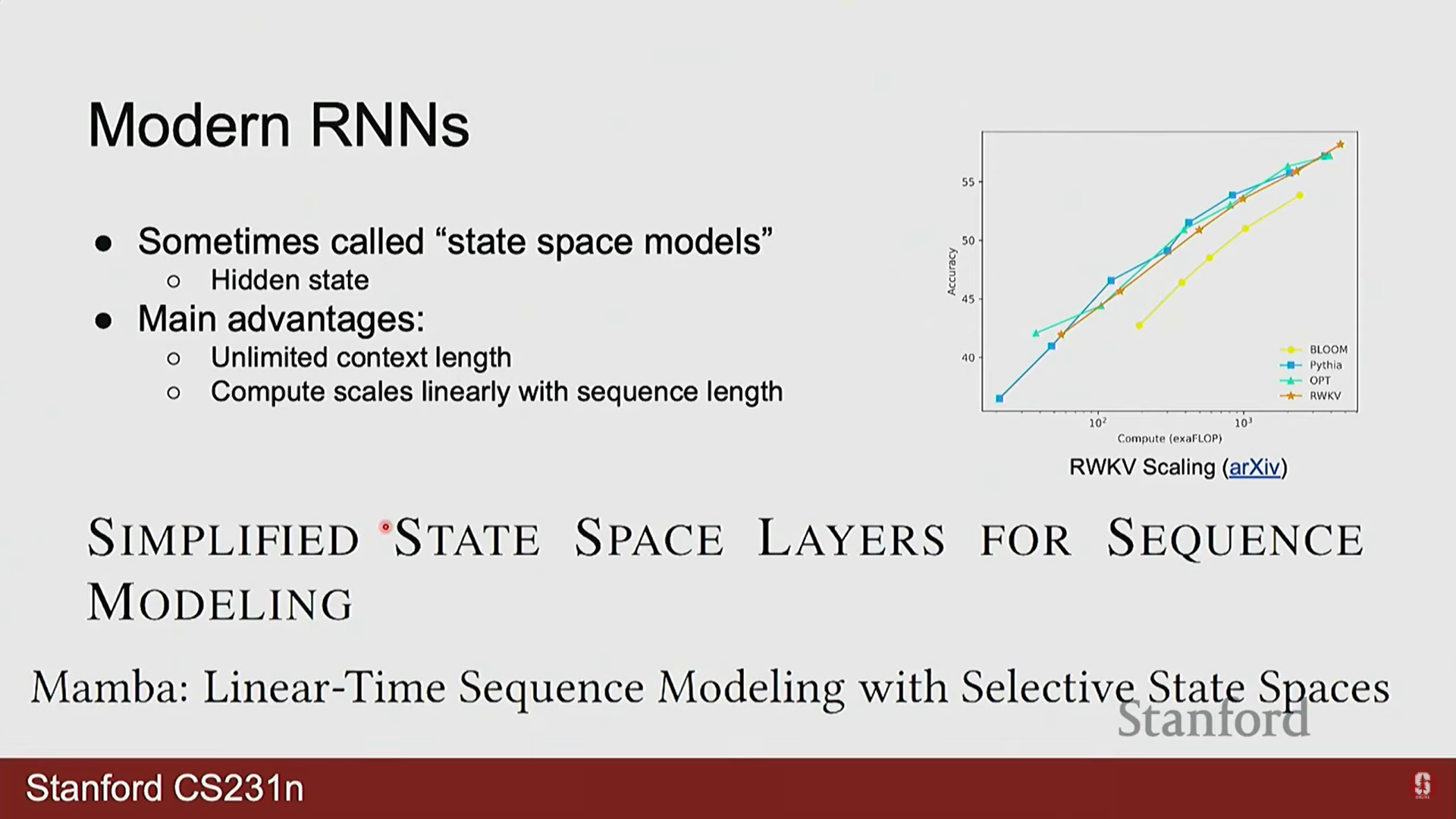
2) RNN의 재조명과 미래
- 한동안 트랜스포머(Transformer) 모델에 밀려났던 RNN이 최근 다시 주목받고 있습니다. 이는 트랜스포머의 근본적인 한계 때문입니다.
- RNN의 장점:
- 무한한 컨텍스트 길이: 이론적으로 시퀀스 길이에 제한이 없습니다.
- 선형 계산 복잡도: 계산량이 시퀀스 길이에 따라 선형적으로() 증가하여 매우 효율적입니다.
- 트랜스포머의 단점:
- 고정된 컨텍스트 길이: 정해진 길이의 시퀀스만 처리할 수 있습니다.
- 제곱 계산 복잡도: 계산량이 시퀀스 길이에 따라 제곱으로() 증가하여 긴 시퀀스 처리에 비효율적입니다.
- 최신 동향: Mamba와 같은 상태 공간 모델(State-Space Models, SSM)은 RNN의 효율적인 선형 스케일링과 트랜스포머의 강력한 성능을 결합하려는 시도로, 차세대 시퀀스 모델의 유력한 후보로 연구되고 있습니다.
5. 강의 Q&A 심층 분석
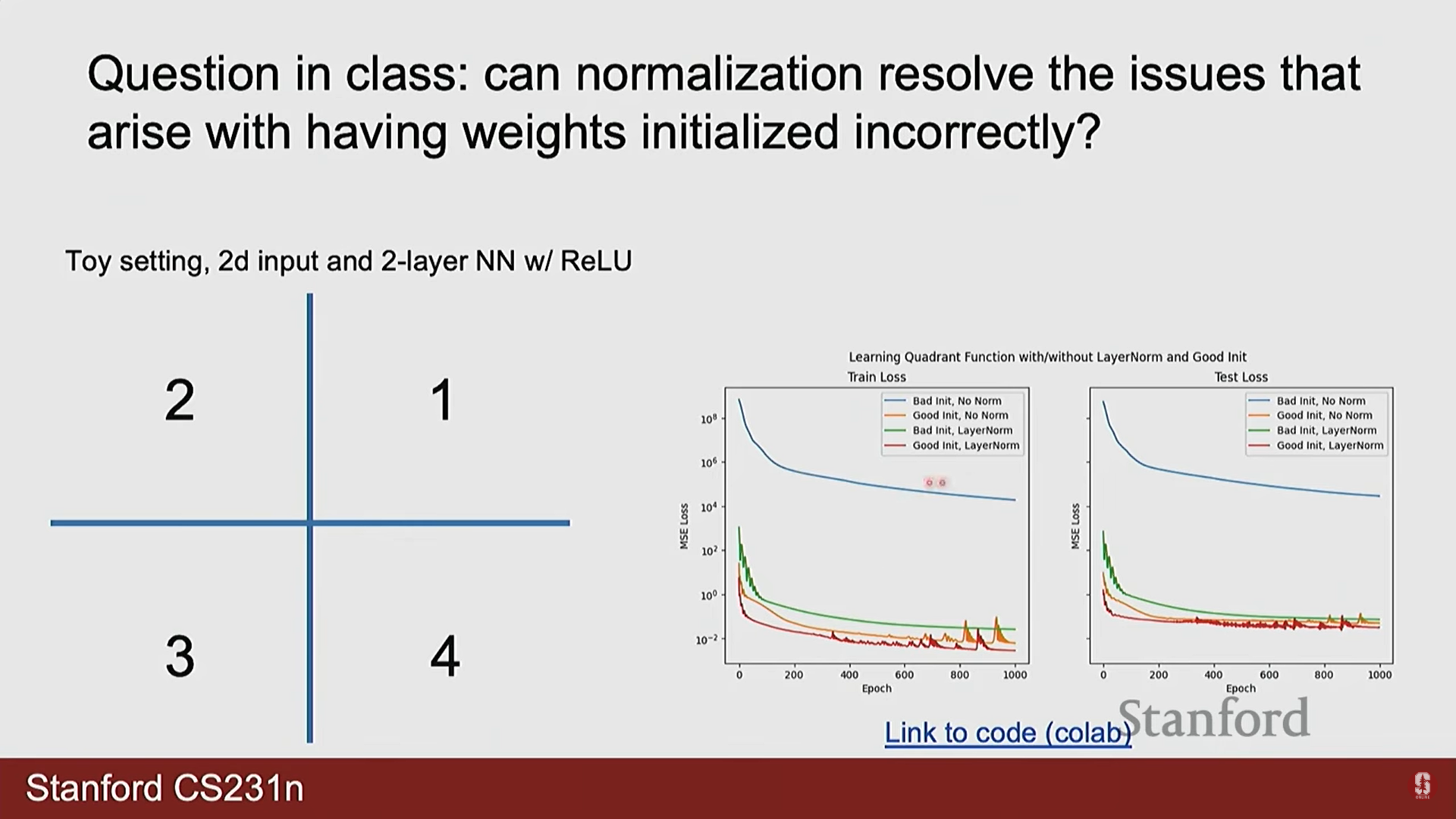
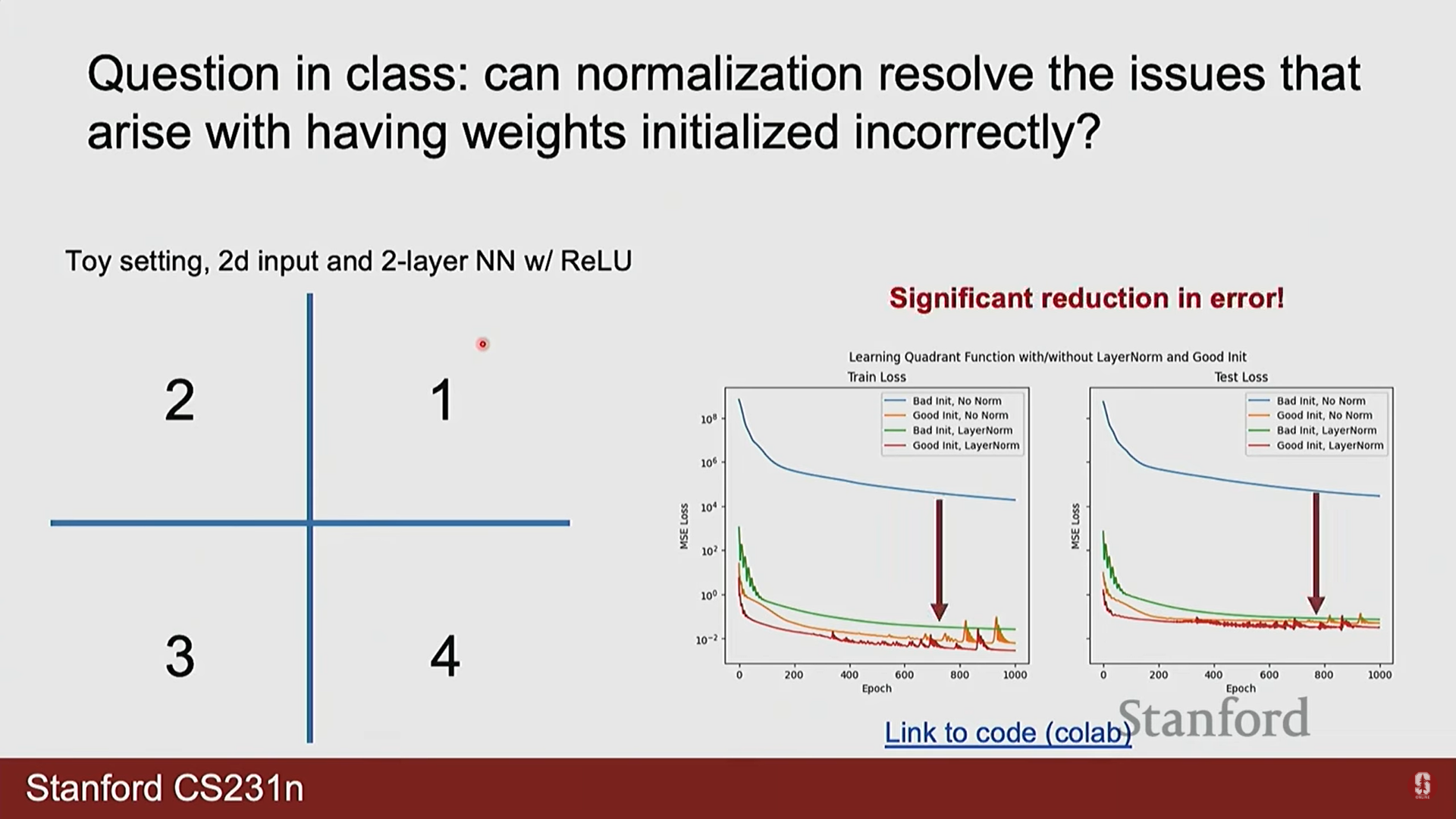
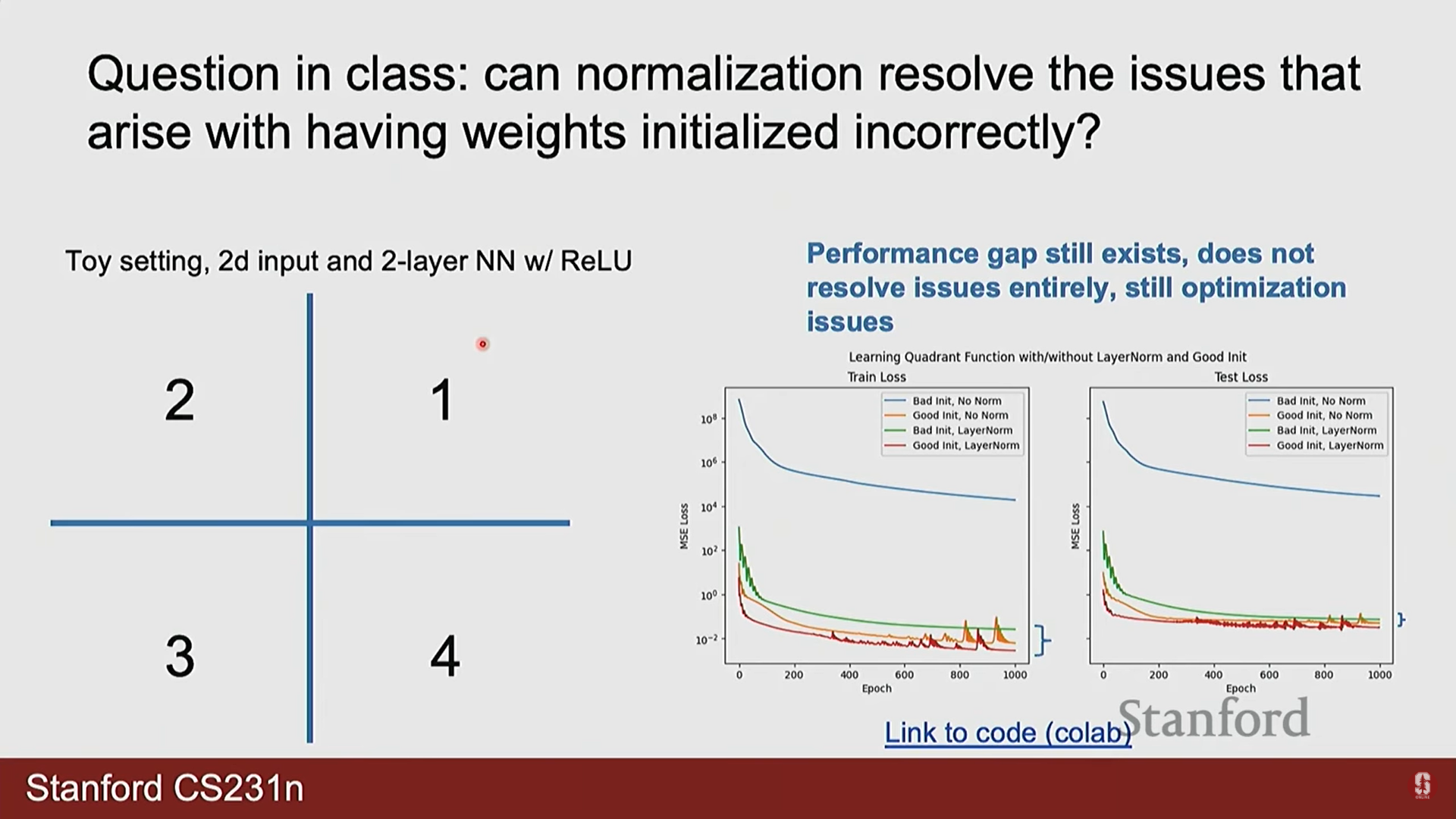
1) Q. 정규화(Normalization)가 잘못된 가중치 초기화 문제를 항상 해결해줍니까?
- A. 부분적으로는 도움이 되지만, 만능 해결책은 아닙니다. 레이어 정규화(Layer Normalization)와 같은 기법은 데이터 분포를 안정화시켜 잘못된 초기화로 인한 문제를 상당 부분 완화할 수 있습니다. 하지만 강의에서 보여준 예시처럼, 최상의 성능을 위해서는 여전히 적절한 가중치 초기화가 필수적입니다. 또한, 정규화는 문제의 종류에 따라 오히려 성능을 저하시킬 수도 있습니다. (예: 입력의 정확한 공간 정보를 보존해야 하는 경우, 정규화가 이 정보를 손상시킬 수 있음)
2) Q. 언어 모델이 항상 최대 확률의 토큰만 선택하면 매번 같은 문장이 생성되지 않습니까?
- A. 네, 정확합니다. 항상 최대 확률 값을 선택하는 방식을 탐욕적 디코딩(Greedy Decoding)이라고 하며, 동일한 시작점에 대해서는 항상 동일한 결과를 생성합니다. 이는 예측 가능하지만, 다양성이 없고 지루한 문장을 만들 수 있습니다. 그래서 실제로는 소프트맥스 함수가 출력한 확률 분포에 기반하여 다음 토큰을 샘플링(sampling)하는 방식을 더 많이 사용합니다. 이를 통해 같은 시작점이더라도 매번 다른, 더 자연스러운 문장을 생성할 수 있습니다. 빔 서치(Beam Search)와 같은 더 발전된 디코딩 전략도 있습니다.
3) Q. LSTM이 기울기 소실 문제를 완벽하게 해결합니까?
- A. '완벽하게' 해결하지는 못합니다. 하지만 LSTM의 셀 상태(cell state)와 게이트 메커니즘은 정보가 활성화 함수를 거의 거치지 않고 직접 전달될 수 있는 일종의 '정보 고속도로'를 제공합니다. 이는 기울기가 여러 시점에 걸쳐 희석되지 않고 효과적으로 전달되는 것을 훨씬 용이하게 만들어, 바닐라 RNN에 비해 장기 의존성 학습 능력을 대폭 향상시킵니다. 경험적으로 이 구조가 매우 효과적인 것으로 입증되어 오랫동안 표준으로 사용되었습니다.

4) Q. 다층(Multi-layer) RNN에서 가중치는 어떻게 공유되나요?
- A. 다층 RNN에서 가중치 공유는 각 '층(layer)' 내에서만 이루어집니다. 예를 들어 3층짜리 RNN이 있다면, 1층의 모든 시점에서는 1층의 가중치()가 공유되고, 2층의 모든 시점에서는 2층의 가중치()가 공유됩니다. 즉, 층과 층 사이에는 서로 다른 가중치가 사용되지만, 각 층 내의 시간 축을 따라서는 동일한 가중치가 공유되는 구조입니다.
