[CV] CS236 14강 정리 [Energy Based Models]

CV

목록 보기

32/32

1. 개요 및 스코어 매칭의 확장 (Introduction & Scalable Score Matching)

지난 강의에 이어 스코어 기반 모델(Score-based Models)에 대한 논의를 심화합니다. 스코어 모델은 신경망을 통해 데이터 분포의 로그 우도 그라디언트(Vector Field, $\nabla_x \log p(x)$ )를 학습하는 것을 목표로 합니다. 그러나 기본적인 스코어 매칭은 고차원 데이터에서 야코비안(Jacobian)의 트레이스(Trace)를 계산해야 하므로 연산량이 과도하여 실제 적용이 어렵다는 한계가 있었습니다. 이를 해결하기 위한 확장된 기법들을 정리합니다.

1.1. 디노이징 스코어 매칭 (Denoising Score Matching, DSM)

개념: 깨끗한 데이터 $x$ 에 노이즈를 더해 $\tilde{x}$ 를 만들고, 이 노이즈 섞인 데이터 분포의 스코어를 추정합니다. 이는 수학적으로 노이즈 $z$ 를 예측하는 디노이징(Denoising) 문제와 동치입니다.
장점: 야코비안 계산이 필요 없어 계산 효율성이 뛰어나며 확장성이 좋습니다.
한계: 원본 데이터 분포 $p_{data}(x)$ 가 아닌, 노이즈가 섞인 분포 $q_\sigma(\tilde{x})$ 의 스코어를 학습한다는 딜레마가 존재합니다.

1.2. 슬라이스드 스코어 매칭 (Sliced Score Matching, SSM)

개념: 야코비안 트레이스를 직접 계산하는 대신, 임의의 랜덤 벡터 $v$ 를 샘플링하여 그 방향으로의 사영(Projection)을 이용해 스코어를 근사하는 방법입니다.
원리: 추정된 스코어와 실제 스코어가 같다면, 임의의 방향 $v$ 로 투영했을 때의 값도 같아야 한다는 성질을 이용합니다. 이를 통해 모델 파라미터만으로 최적화 가능한 손실 함수를 유도할 수 있습니다.
특징:
- 데이터에 인위적인 노이즈를 섞지 않고 원본 데이터 분포(True data density)의 스코어를 직접 추정할 수 있다는 장점이 있습니다.
- 야코비안 트레이스 계산보다는 효율적이지만, 여전히 역전파를 통한 미분 계산(Directional derivatives)이 필요하므로 DSM보다는 학습 속도가 다소 느립니다.

2. 랑주뱅 역학의 한계와 해결책 (Limitations & Solutions in Langevin Dynamics)

학습된 스코어를 이용해 랑주뱅 역학(Langevin Dynamics)으로 샘플링할 때, 고차원 데이터에서는 다음과 같은 세 가지 문제로 인해 실패하게 됩니다.

2.1. 주요 문제점

매니폴드 가설 (Manifold Hypothesis): 실제 데이터(예: 이미지)는 고차원 공간 전체가 아닌 저차원 매니폴드 위에 존재합니다. 매니폴드를 벗어난 영역에서는 확률이 0에 가까워 스코어가 정의되지 않으며, 이로 인해 랑주뱅 역학이 올바른 방향을 찾지 못합니다.
저밀도 영역의 부정확성 (Low Density Regions): 데이터가 희소한 영역에서는 스코어 추정이 부정확하여, 초기 샘플링 단계에서 엉뚱한 방향으로 이동할 수 있습니다.
느린 혼합 (Slow Mixing): 데이터 분포가 여러 모드(Mode)로 분리된 경우, 모드 사이를 건너뛰어 이동하는 데 매우 오랜 시간이 걸려 수렴하지 못합니다.

2.2. 해결책: 다중 스케일 노이즈 (Multi-Scale Noise)

위의 문제들을 해결하는 핵심 아이디어는 데이터에 노이즈를 추가하는 것입니다.

노이즈의 효과: 데이터에 가우시안 노이즈를 더하면, 데이터 분포가 전체 공간으로 퍼지게 되어 매니폴드 밖에서도 확률 밀도가 정의됩니다. 이로 인해 스코어 매칭이 훨씬 안정적으로 변합니다.
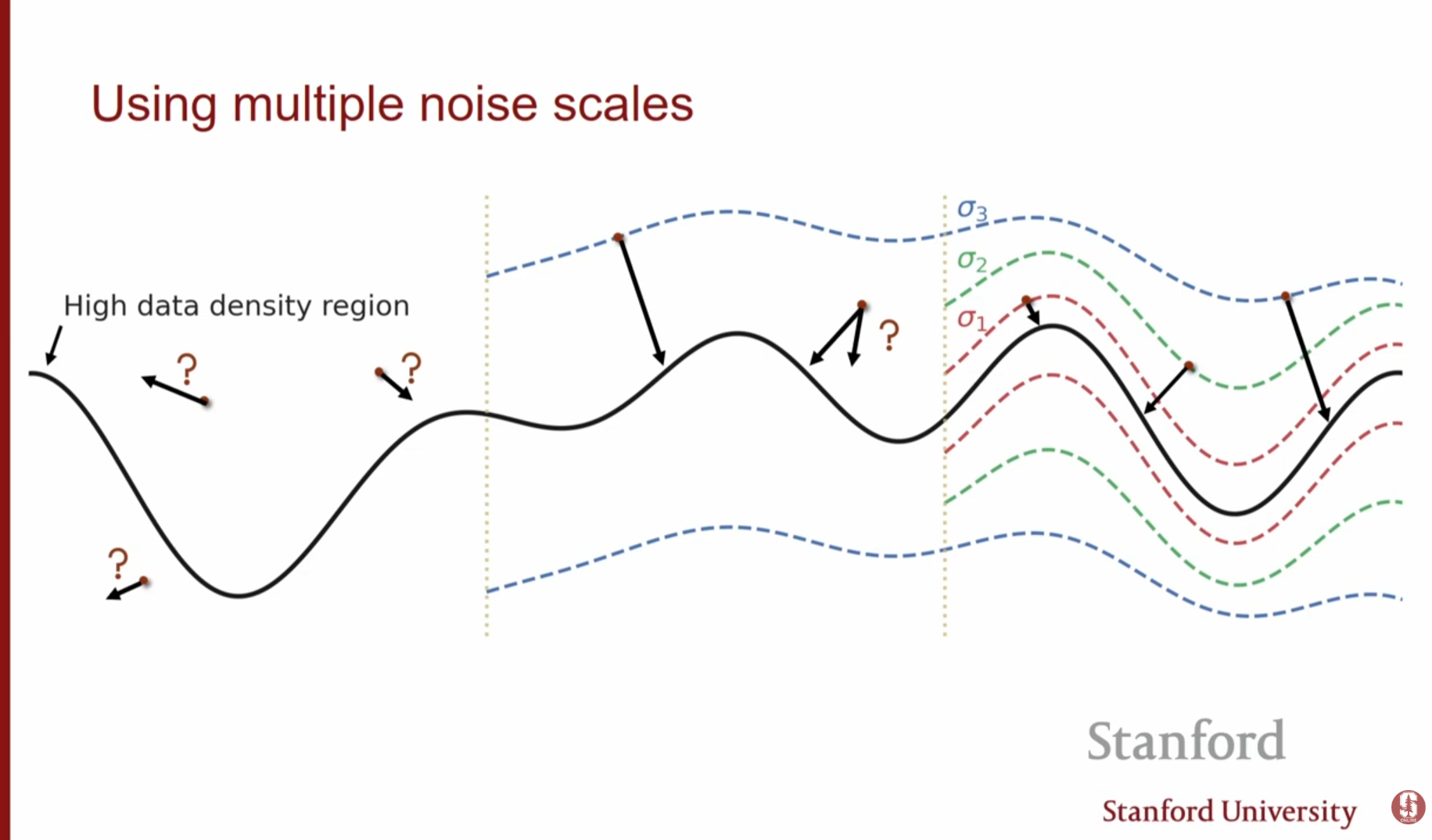
트레이드오프(Trade-off):
- 노이즈가 작으면: 원래 데이터 분포와 비슷하지만, 여전히 저밀도 영역 문제가 남아있어 스코어 추정이 불안정합니다.
- 노이즈가 크면: 스코어 추정은 쉽고 정확해지지만, 원본 데이터의 구조가 파괴되어 우리가 원하는 이미지를 얻을 수 없습니다.

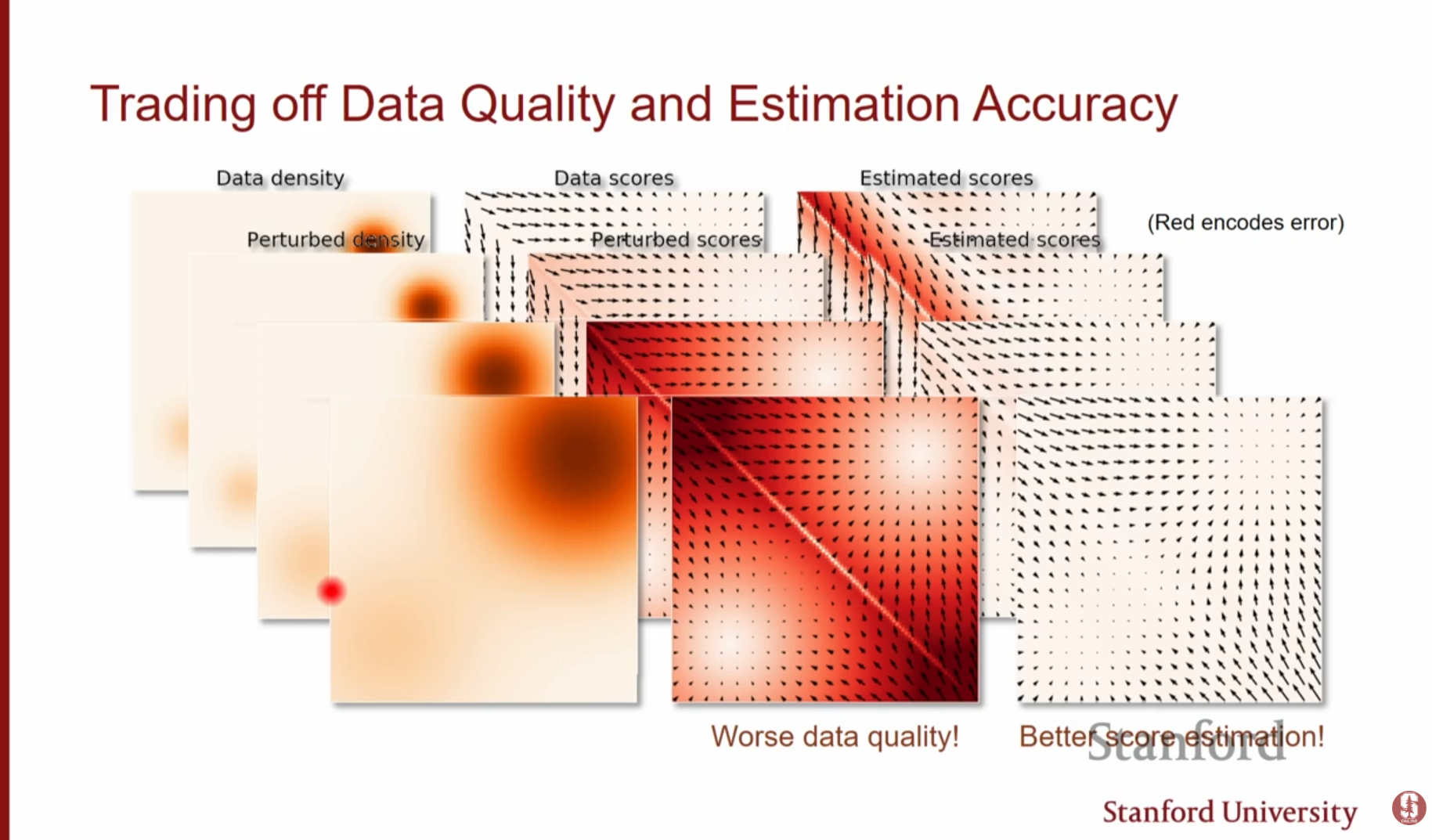
심화 내용: 노이즈 스케일의 역할

단일 노이즈 레벨로는 충분하지 않습니다. 우리는 노이즈가 매우 큰 상태(쉬운 추정, 넓은 탐색)부터 노이즈가 거의 없는 상태(정교한 구조)까지를 모두 활용해야 합니다. 이를 위해 다양한 크기의 노이즈 레벨 $\sigma_1, \sigma_2, \dots, \sigma_L$ 을 정의하고 이를 순차적으로 활용합니다.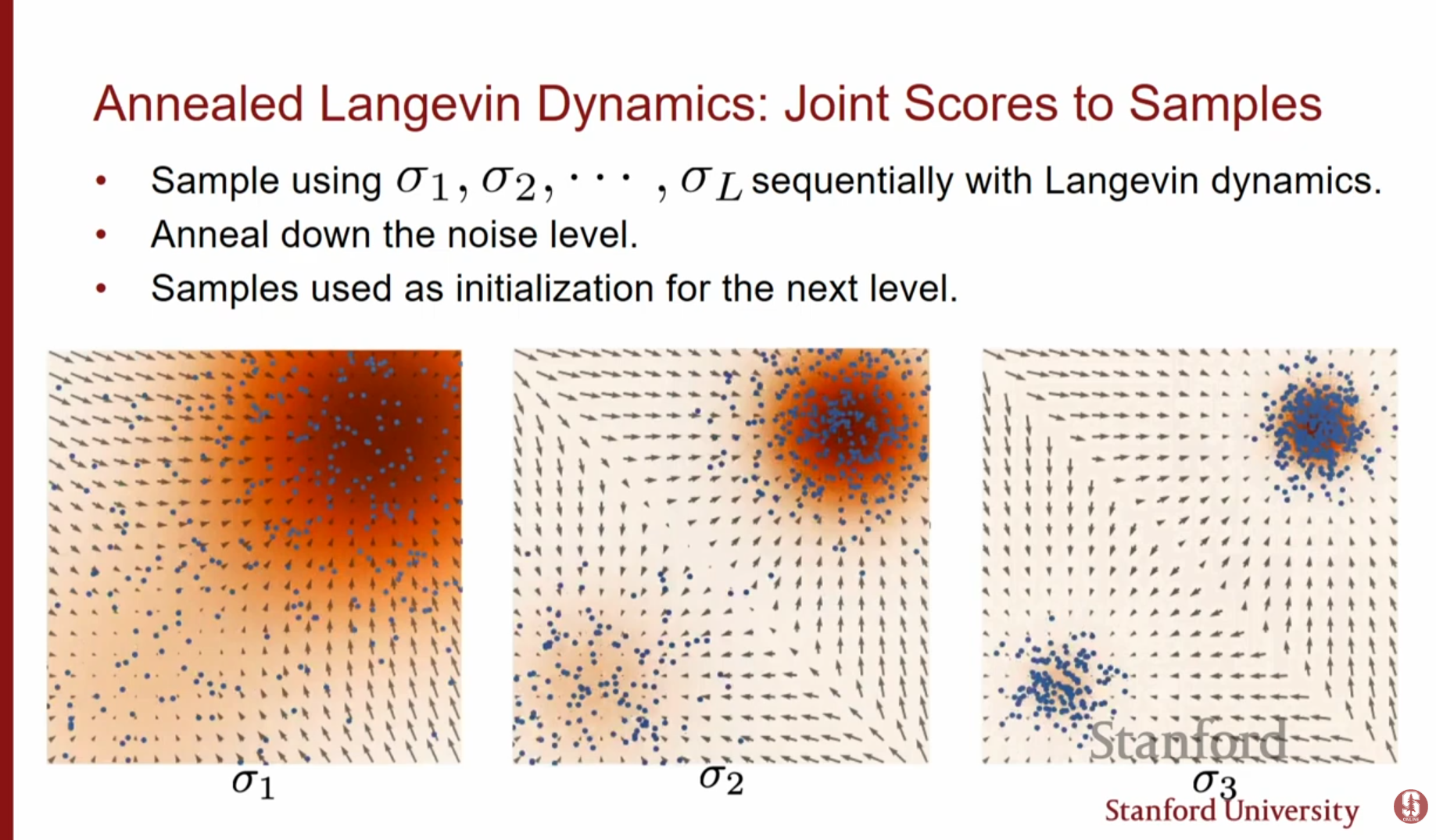

3. NCSN과 학습 전략 (NCSN & Training Strategy)

이 아이디어를 구현한 것이 Noise Conditional Score Network (NCSN)입니다.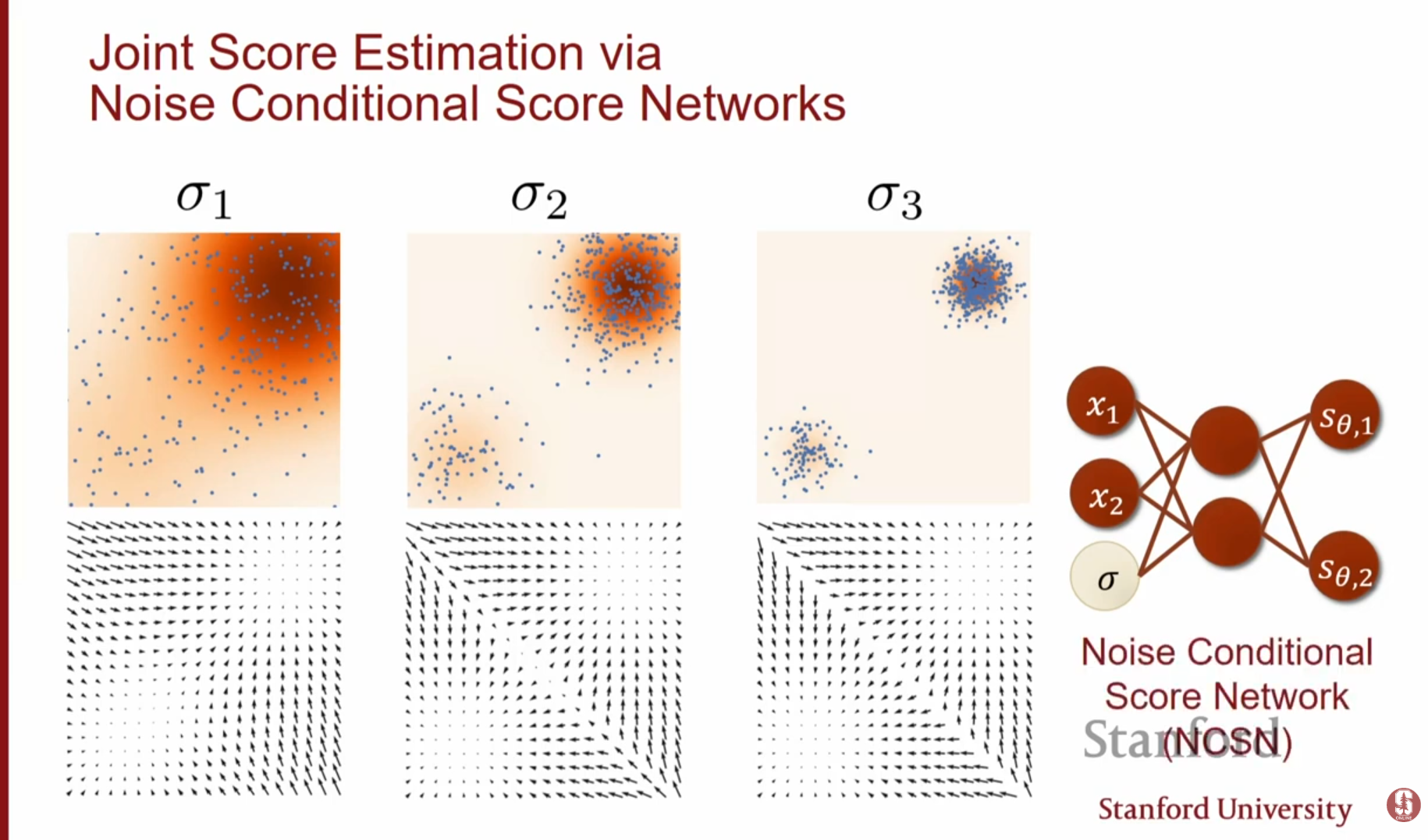

3.1. 모델 구조 및 손실 함수

단일 신경망 $s_\theta(x, \sigma)$ 가 데이터 $x$ 와 노이즈 레벨 $\sigma$ 를 동시에 입력받아, 해당 레벨의 스코어를 출력하도록 학습합니다. 전체 손실 함수는 각 노이즈 레벨에서의 DSM 손실의 가중 합입니다.
$\mathcal{L} = {1 \over L} \sum_{i=1}^{L} \lambda(\sigma_i) \mathbb{E}_{x, z} \left[ \left\| s_\theta(x + \sigma_i z, \sigma_i) + \frac{z}{\sigma_i} \right\|_2^2 \right]$

3.2. 가중치 함수 (Weighting Function) 선택

손실 함수에서 각 노이즈 레벨의 기여도를 조절하는 $\lambda(\sigma_i)$ 의 설정은 매우 중요합니다.

이유: 스코어( $\nabla \log p$ )의 크기는 대략 $1/\sigma$ 에 비례합니다. 즉, 노이즈가 작을수록 스코어 값은 매우 커지고, 노이즈가 클수록 작아집니다.
설정: 일반적으로 $\lambda(\sigma_i) = \sigma_i^2$ 로 설정합니다. 이렇게 하면 스코어의 크기( $1/\sigma$ )와 가중치( $\sigma^2$ )가 상쇄되어, 모든 노이즈 레벨에서의 손실 값 스케일이 균등해집니다(Order of 1). 이는 모델이 특정 노이즈 레벨에 치우치지 않고 전체를 고르게 학습하도록 돕습니다.

3.3. 하이퍼파라미터 설정 (Hyperparameters)

최대 노이즈( $\sigma_{max}$ ): 데이터 포인트 간의 최대 거리(Maximum pairwise distance)만큼 커야 합니다. 그래야 분포가 충분히 퍼져 모든 모드 간 이동이 가능해집니다.
최소 노이즈( $\sigma_{min}$ ): 원본 데이터와 구별할 수 없을 만큼 충분히 작아야 합니다.
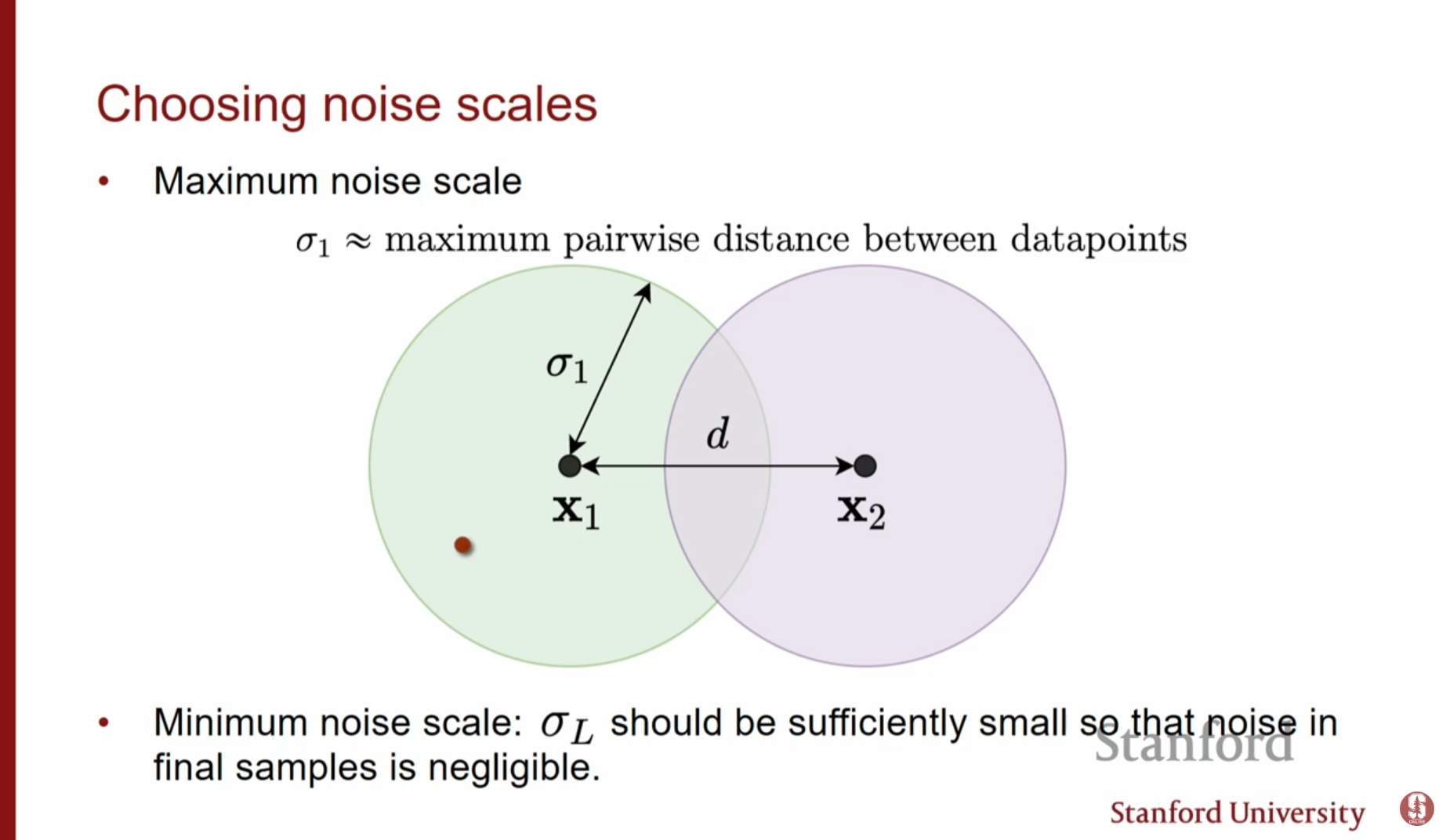
스케일 간격: 기하급수적(Geometric progression)으로 설정합니다. 이는 인접한 노이즈 레벨 간 분포가 적절히 겹치게(Overlap) 하여, 이전 단계의 샘플이 다음 단계의 좋은 초기값이 되도록 보장합니다.

3.4. 어닐링 랑주뱅 역학 (Annealed Langevin Dynamics)

샘플링 시 $\sigma_1$ (큰 노이즈)에서 시작하여 $\sigma_L$ (작은 노이즈)까지 순차적으로 랑주뱅 역학을 수행합니다. 초기에는 전체적인 구조를 잡고(Mixing), 점차 세부적인 디테일을 복원합니다.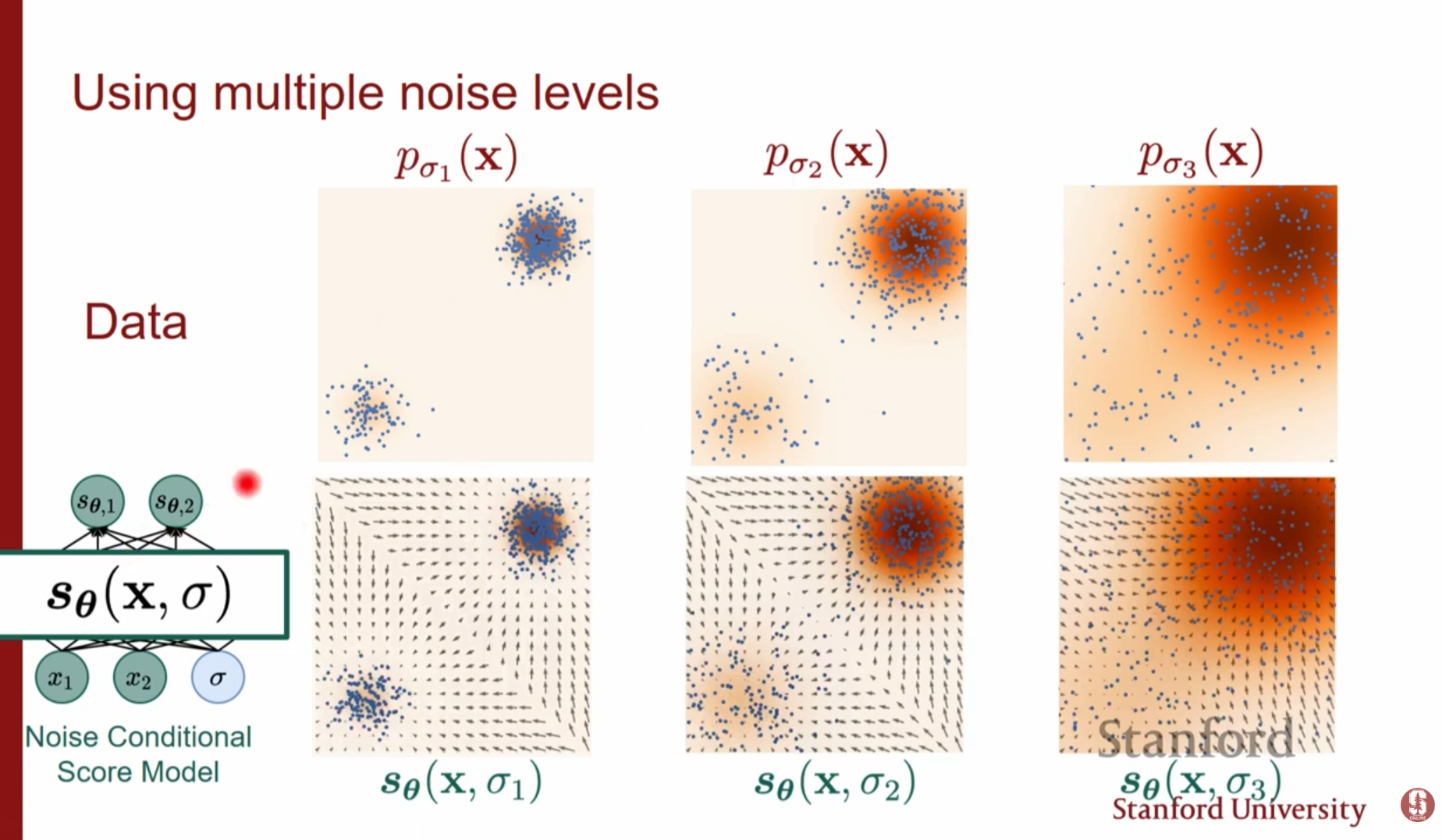

4. 연속 시간 확산 모델: SDE로의 확장 (Diffusion Models as SDEs)

노이즈 레벨의 개수 $L$ 을 무한대로 늘리면( $L \to \infty$ ), 이산적인 단계가 아닌 연속적인 시간 $t \in [0, T]$ 에 대한 확률 미분 방정식(Stochastic Differential Equation, SDE)으로 과정을 기술할 수 있습니다.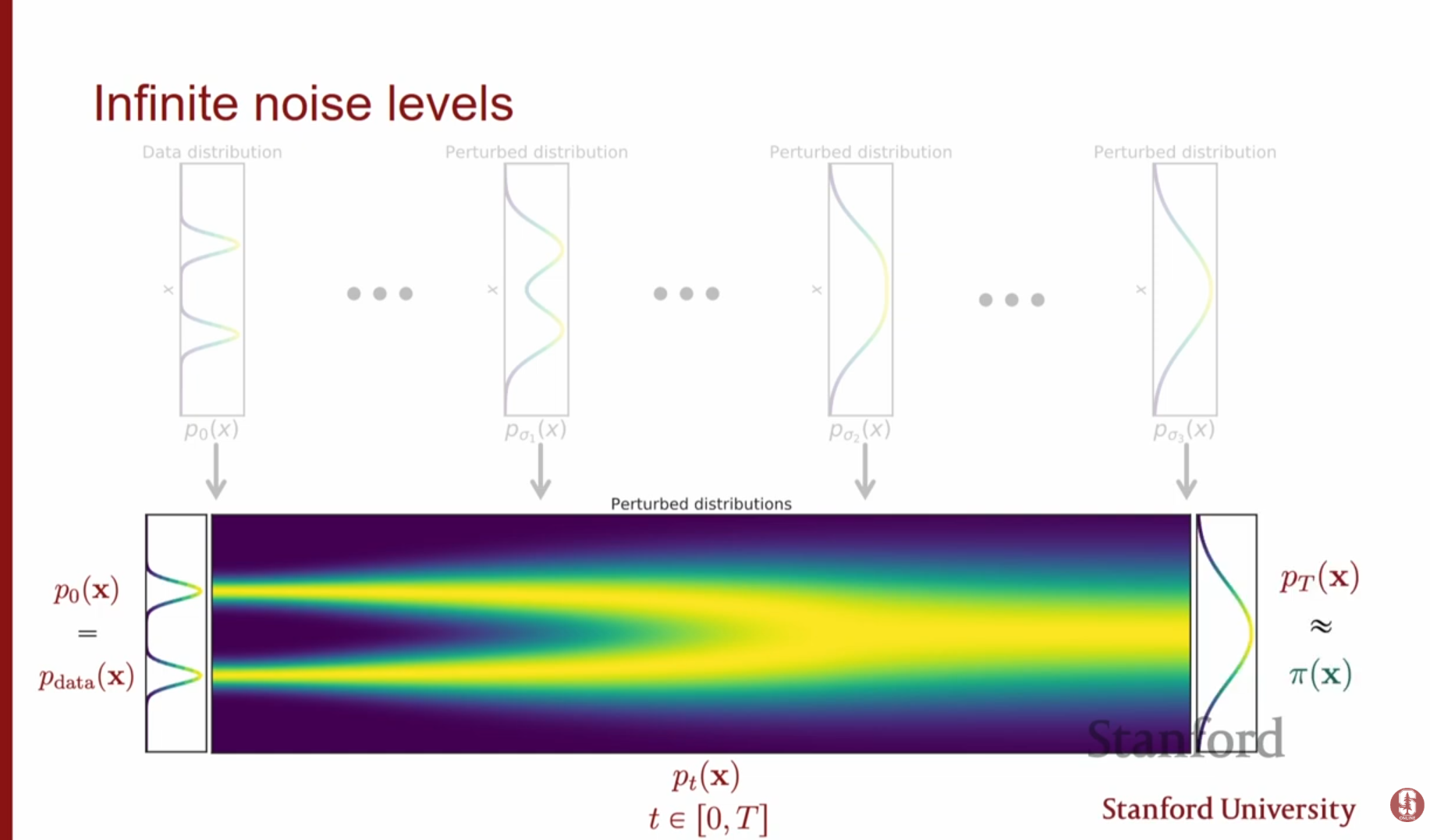

4.1. 순방향 SDE (Forward SDE)

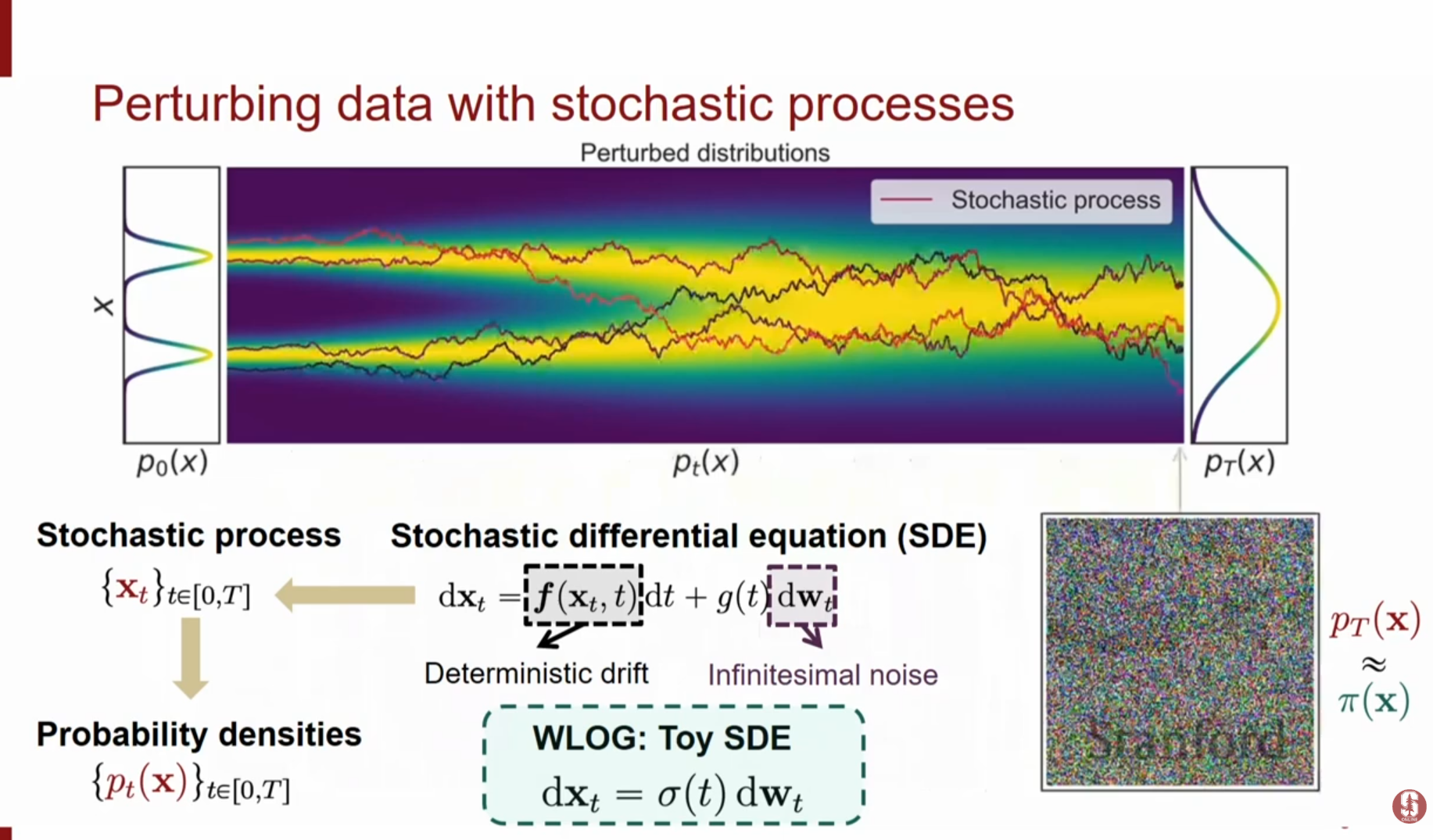
데이터에서 노이즈로 가는 확산 과정은 다음과 같은 SDE로 표현됩니다.
$d\mathbf{x_t} = \mathbf{f}(\mathbf{x_t}, t)dt + g(t)d\mathbf{w_t}$

WLOG(Without Loss Of Generality) : Toy SDE는 다음과 같이 표현됩니다.
$d\mathbf{x_t} = \sigma(t)d\mathbf{w_t}$

$\mathbf{f}(\mathbf{x}, t)$ : Drift coefficient (데이터의 결정론적 이동 경향)
$g(t)$ : Diffusion coefficient (노이즈의 크기 조절)
$d\mathbf{w}$ : 브라운 운동(Wiener process)에 의한 미소 노이즈
시간이 지날수록( $T \to \infty$ ) 데이터 분포는 점차 사전 분포(Prior distribution, 예: 순수 가우시안 노이즈)로 수렴합니다.

4.2. 역방향 SDE (Reverse SDE)

생성을 위해 시간을 거꾸로 돌리는( $T \to 0$ ) 과정 또한 SDE로 기술할 수 있습니다. Anderson(1982) 등의 연구에 따르면 역방향 SDE는 다음과 같습니다.
$d\mathbf{x_t} = [\mathbf{f}(\mathbf{x_t}, t) - g(t)^2 \nabla_\mathbf{x} \log p_t(\mathbf{x_t})] dt + g(t) d\bar{\mathbf{w_t}}$

WLOG(Without Loss Of Generality) : Toy Reverse SDE는 다음과 같이 표현됩니다.
$d\mathbf{x_t} = [- \sigma(t)^2 \nabla_\mathbf{x} \log p_t(\mathbf{x_t})] dt + \sigma (t)d\bar{\mathbf{w_t}}$

$d\bar{\mathbf{w}}$ : 역방향 시간에서의 브라운 운동
핵심: 역방향 과정을 시뮬레이션하기 위해서는 각 시점 $t$ 에서의 스코어 함수 $\nabla_\mathbf{x} \log p_t(\mathbf{x})$ 를 알아야 합니다. 우리가 학습한 스코어 모델 $s_\theta(x, t)$ 를 이 식에 대입하여 수치적으로 풀면 데이터를 생성할 수 있습니다.

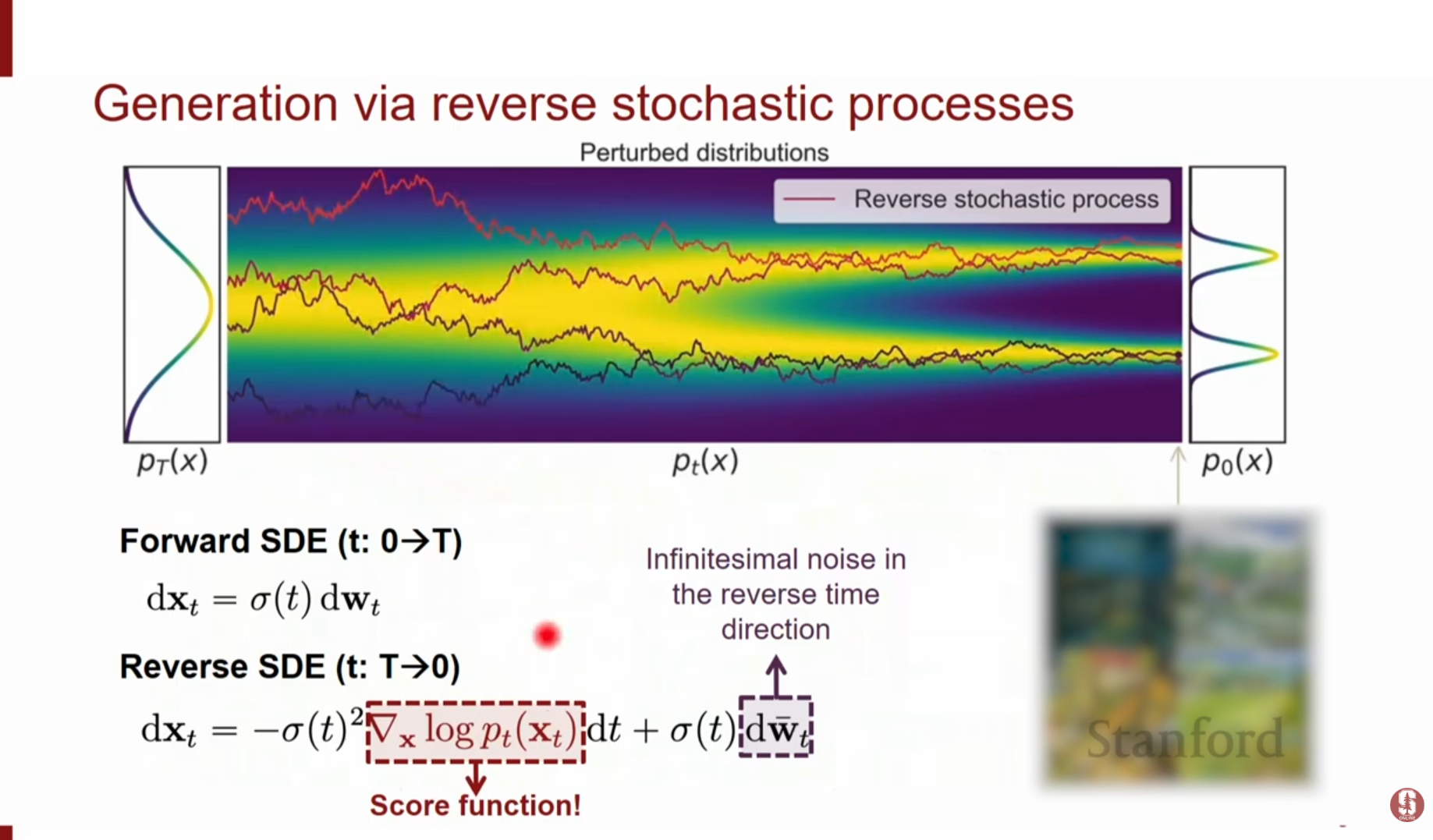
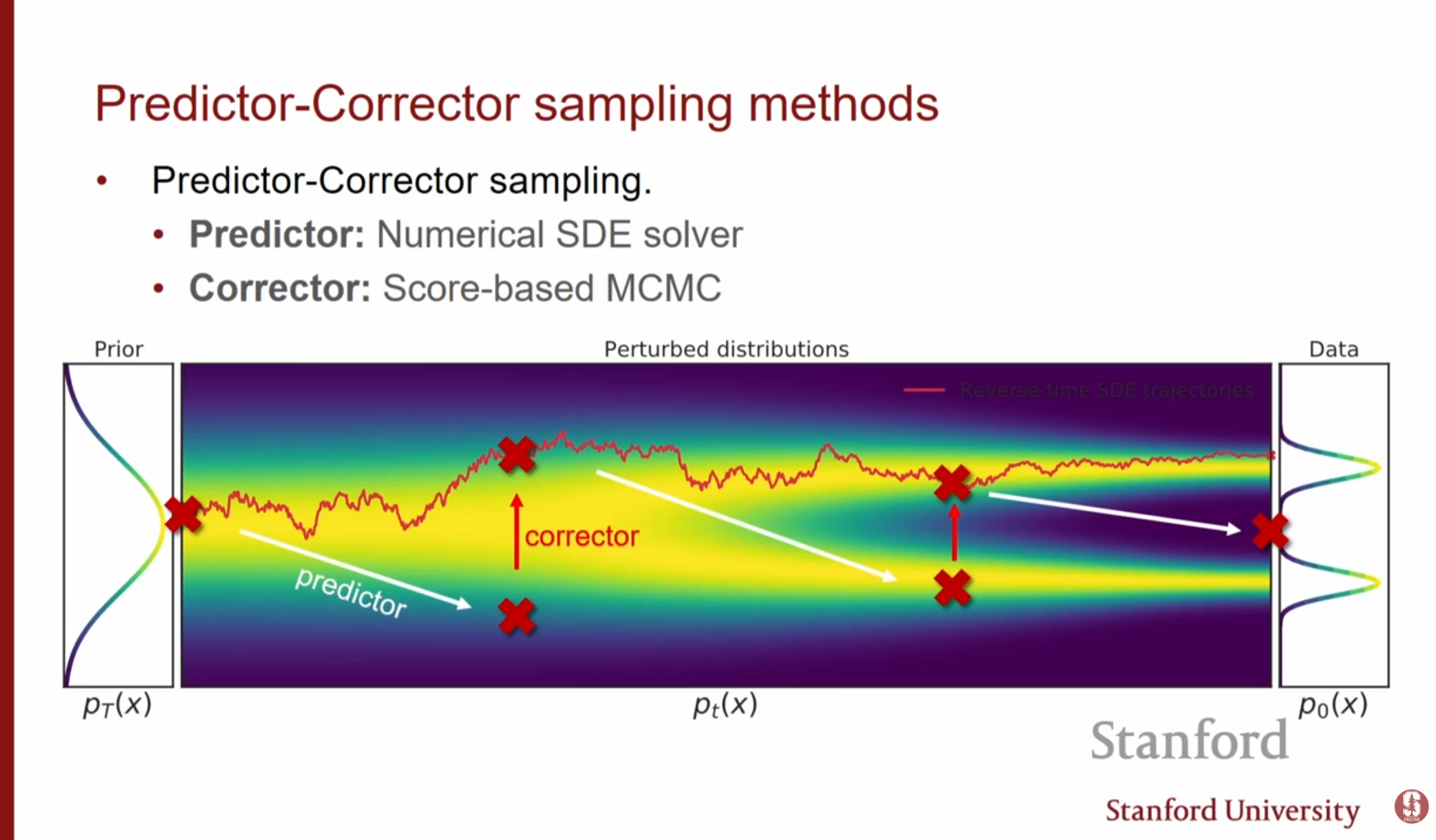
4.3. 수치적 풀이 (Numerical Solvers)

역방향 SDE를 풀기 위해 다양한 수치 해석 기법을 사용합니다.

Euler-Maruyama: 가장 기본적인 방법으로, 시간을 잘게 쪼개어(Discretize) 순차적으로 업데이트합니다.
Predictor-Corrector: 수치적 솔버(Predictor)로 대략적인 위치를 이동한 뒤, 랑주뱅 역학(Corrector)을 사용해 분포를 보정하는 방식을 결합하여 샘플 품질을 높입니다.

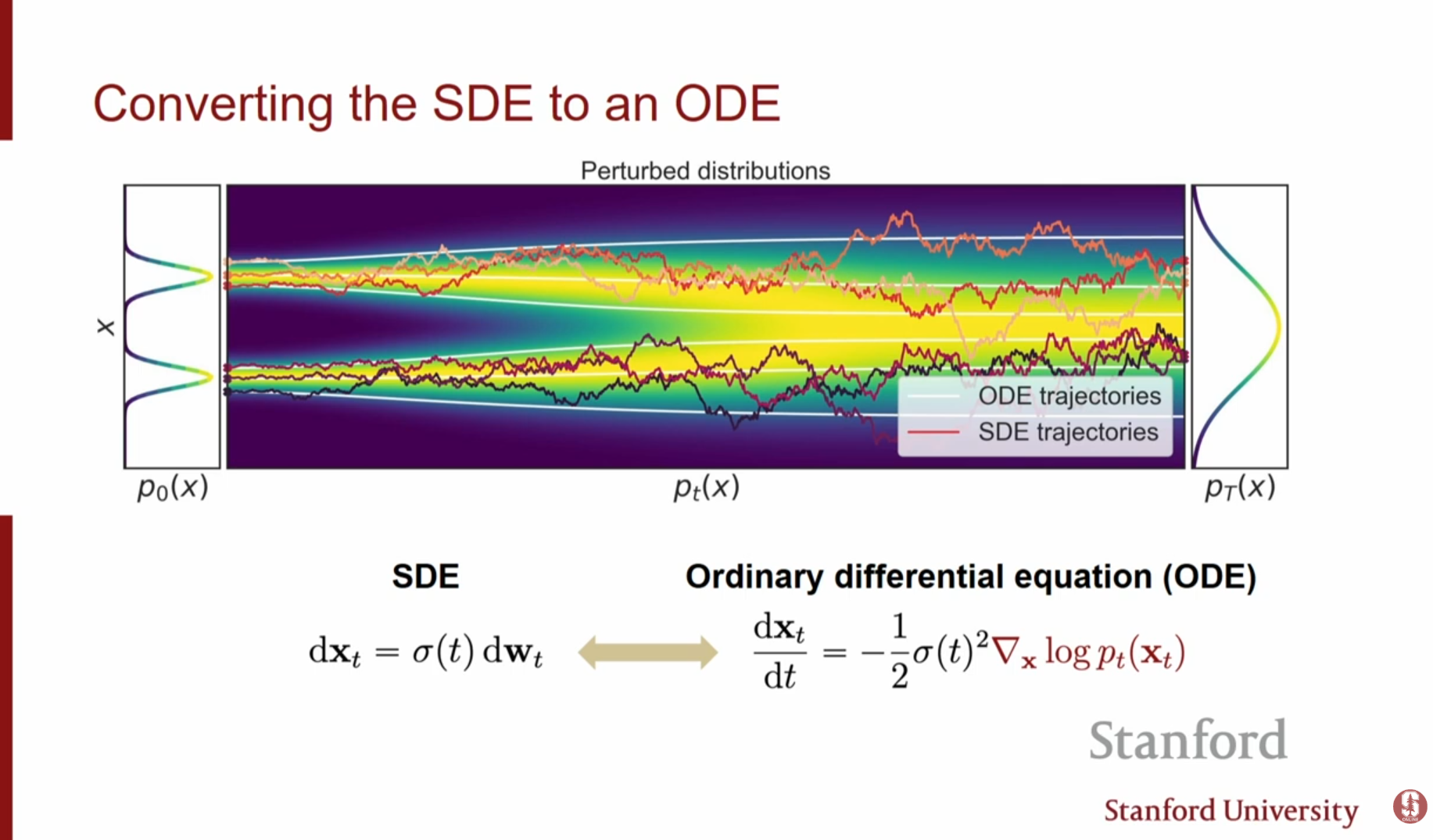
5. 확률 흐름 ODE (Probability Flow ODE)

SDE와 동일한 주변 확률 분포(Marginal Distribution) $p_t(x)$ 를 가지면서도, 노이즈 항이 없는 결정론적(Deterministic)인 상미분 방정식(ODE)이 존재합니다.

5.1. 특징 및 의의

공식: SDE 식에서 노이즈 항을 제거하고 스코어 항을 조정한 형태입니다.
결정론적 궤적: 궤적(Trajectory)이 서로 교차하지 않으므로, 초기 노이즈 벡터와 생성된 데이터 간에 역변환이 가능한 1:1 매핑이 형성됩니다.
정규화 흐름(Normalizing Flow)과의 연결: 이를 통해 확산 모델을 연속 시간 정규화 흐름(Continuous-time Normalizing Flow)으로 해석할 수 있습니다. 이 관점에서는 정확한 우도(Exact Likelihood) 계산이 가능하며, 이미지를 잠재 공간(Latent space)으로 인코딩하거나 조작하는 것이 가능해집니다.

6. 강의 Q&A (Q&A Session)

Q1: 디노이징 스코어 매칭(DSM)과 단순히 노이즈를 추가하는 것이 어떻게 다른가요?

A: DSM을 사용해 노이즈 섞인 데이터의 스코어를 학습하면, 결국 노이즈가 섞인 이미지를 생성하게 됩니다. 우리의 목표는 깨끗한 이미지를 얻는 것이므로, DSM만으로는 부족합니다. 따라서 아주 큰 노이즈부터 작은 노이즈까지 다양한 레벨을 동시에 학습하여, 최종적으로는 노이즈가 거의 없는 깨끗한 데이터를 얻도록 설계하는 것이 핵심입니다.

Q2: 실제 데이터가 저차원 매니폴드에 있다는 것은 무슨 뜻인가요?

A: 이미지의 픽셀들은 서로 독립적이지 않습니다. 예를 들어, 눈 주변 픽셀이 결정되면 다른 부분도 제약을 받습니다. 즉, 모든 가능한 픽셀 조합 중 '실제 이미지'처럼 보이는 것은 극히 일부의 표면(Surface) 위에만 존재하며, 이 표면을 벗어나면 확률이 0이 되어 스코어가 정의되지 않습니다.

Q3: 확산 모델이 GAN보다 좋은 점은 무엇인가요?

A: 이론적으로 더 우월하다는 증명은 없지만, 학습의 안정성이 큰 장점입니다(Minimax 게임 없음). 또한, 추론 시 많은 계산(반복적인 스텝)을 사용할 수 있어 더 높은 품질의 이미지를 생성할 수 있습니다. 즉, 깊은 연산 그래프를 추론 시에만 활용하는 구조입니다.

Q4: 손가락 생성 문제(Fingers problem)는 왜 발생하나요?

A: 생성 모델이 손가락 개수 등을 정확히 맞추지 못하는 경우가 많습니다. 이는 데이터셋 내에서 손가락이 매우 다양한 각도와 형태로 등장하여 모델이 일관된 구조를 학습하기 어렵기 때문일 수 있습니다. 하지만 대규모 데이터와 학습을 통해 점차 개선되고 있습니다.

Q5: 모델이 학습 데이터를 단순히 암기(Overfitting)하는 것은 아닌가요?

A: 검증 데이터셋(Validation Set)에 대한 손실을 확인하거나, 생성된 이미지와 가장 가까운 학습 이미지를 비교(Nearest Neighbor)해보면 단순 암기가 아님을 알 수 있습니다. 단, 텍스트-이미지 모델의 경우 특정 프롬프트에 대해 훈련 데이터를 그대로 뱉어내는 과적합 현상이 일부 관찰되기도 합니다.

7. 핵심 내용 요약 (Core Summary)

스코어 매칭의 진화: 기존 방식의 계산 문제를 해결하기 위해 디노이징 스코어 매칭(DSM)과 슬라이스드 스코어 매칭(SSM)이 사용되며, 특히 DSM은 노이즈 추가를 통해 매니폴드 밖에서의 스코어 추정 문제를 해결하는 기반이 됩니다.
NCSN과 가중치 전략: 다양한 노이즈 레벨을 단일 신경망으로 학습하며, 이때 $\lambda(\sigma) = \sigma^2$ 가중치를 사용하여 스코어 스케일 차이를 보정하고 안정적인 학습을 보장합니다.
SDE 기반 생성 프레임워크: 확산 과정을 연속 시간 SDE(순방향/역방향)로 모델링하여, 학습된 스코어 함수를 역방향 SDE 식에 대입함으로써 순수 노이즈로부터 데이터를 복원하는 강력하고 유연한 생성 모델을 구축합니다.

김성윤(Jack)

AI 공부합니다

이전 포스트