[CV] CS236 13강 정리 [Score Based Models]

김성윤(Jack)·약 11시간 전

CV

목록 보기

31/32

1. 생성 모델의 분류와 스코어 기반 모델의 도입

기존 생성 모델의 흐름과 한계

강의 초반부에서는 지금까지 다룬 생성 모델들의 장단점을 복습하며 스코어 기반 모델의 필요성을 설명합니다.

우도 기반 모델(Likelihood-based models): Autoregressive 모델이나 Flow 모델 등은 확률 밀도 함수(PDF)를 직접 모델링합니다. 하지만 정규화(Normalization) 조건(적분값이 1이 되어야 함) 때문에 모델 구조에 제약이 생기거나 계산이 어렵습니다.
변분 오토인코더(VAE) 및 에너지 기반 모델(EBM): 정규화 상수를 우회하기 위해 변분 추론이나 근사법을 사용하지만, 여전히 정확한 우도 계산이나 안정적인 학습에 어려움이 있습니다.
암시적 생성 모델(Implicit Generative Models): GAN과 같이 샘플링 과정 자체를 모델링하지만, 생성된 샘플의 우도를 평가하기 어렵고 학습이 불안정(Minimax optimization)하다는 단점이 있습니다.

스코어 기반 모델(Score-Based Models)의 정의

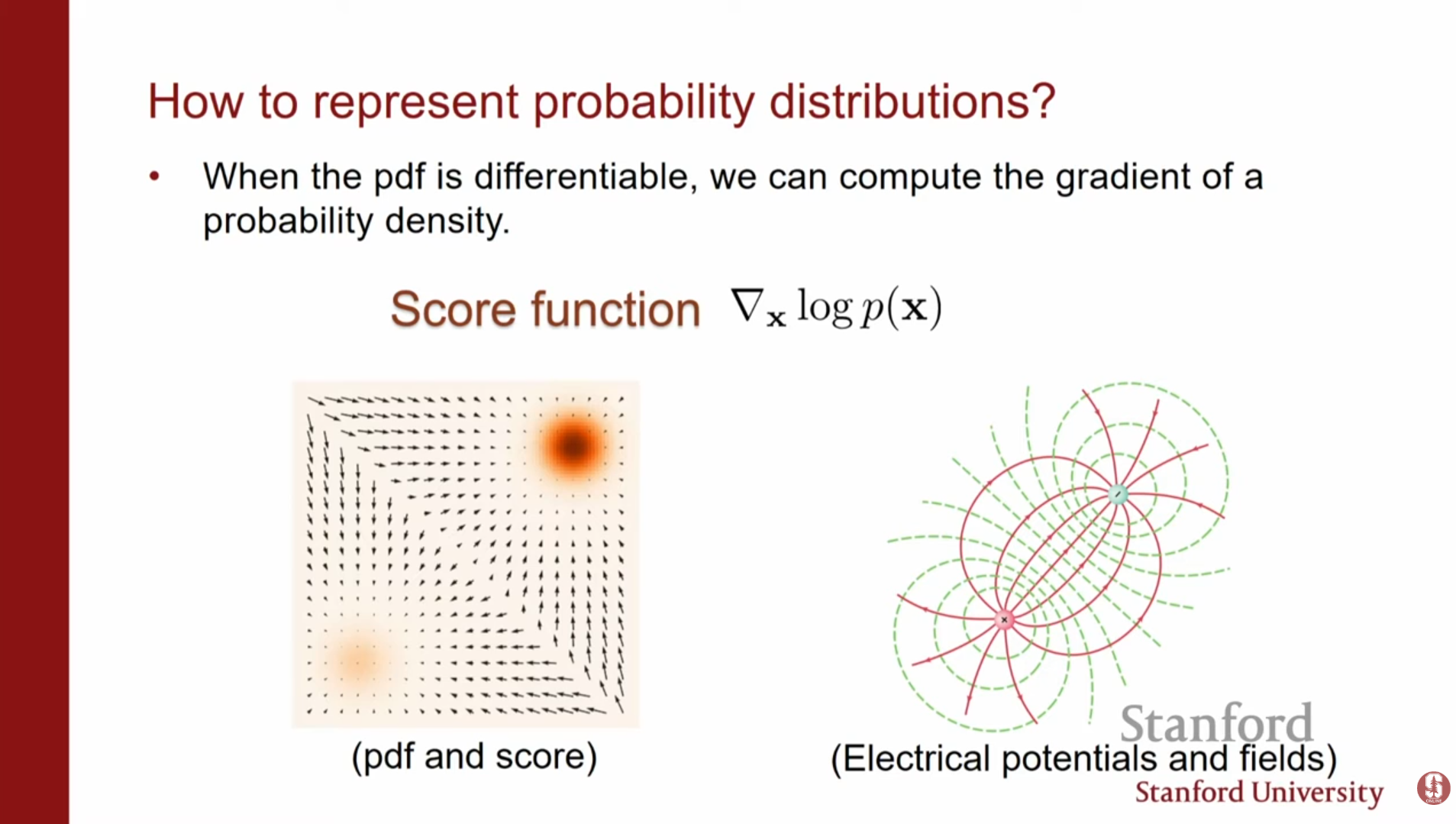
스코어 기반 모델은 확률 밀도 함수 자체가 아니라, 로그 확률 밀도 함수의 기울기(Gradient of log density)를 모델링하는 접근 방식입니다.

스코어 함수(Score Function): 입력 데이터 $x$ 에 대한 로그 우도의 기울기로 정의됩니다.
$s(x) = \nabla_x \log p(x)$
여기서 기울기는 파라미터 $\theta$ 가 아닌 입력 데이터 $x$ 에 대한 것입니다.
핵심 아이디어: PDF를 직접 모델링하는 대신, 각 지점에서 로그 우도를 가장 빠르게 증가시키는 방향(벡터 필드)을 학습합니다. 이는 물리학에서 전기장을 기술하는 것과 유사합니다.
장점: 로그를 취하고 $x$ 에 대해 미분하면 정규화 상수 $Z_\theta$ 가 사라집니다.
$\nabla_x \log \frac{e^{-E_\theta(x)}}{Z_\theta} = \nabla_x (-E_\theta(x)) - \underbrace{\nabla_x \log Z_\theta}_{0} = -\nabla_x E_\theta(x)$
즉, 복잡한 정규화 상수를 계산할 필요 없이 모델링이 가능합니다.

2. 스코어 매칭(Score Matching): 학습 방법

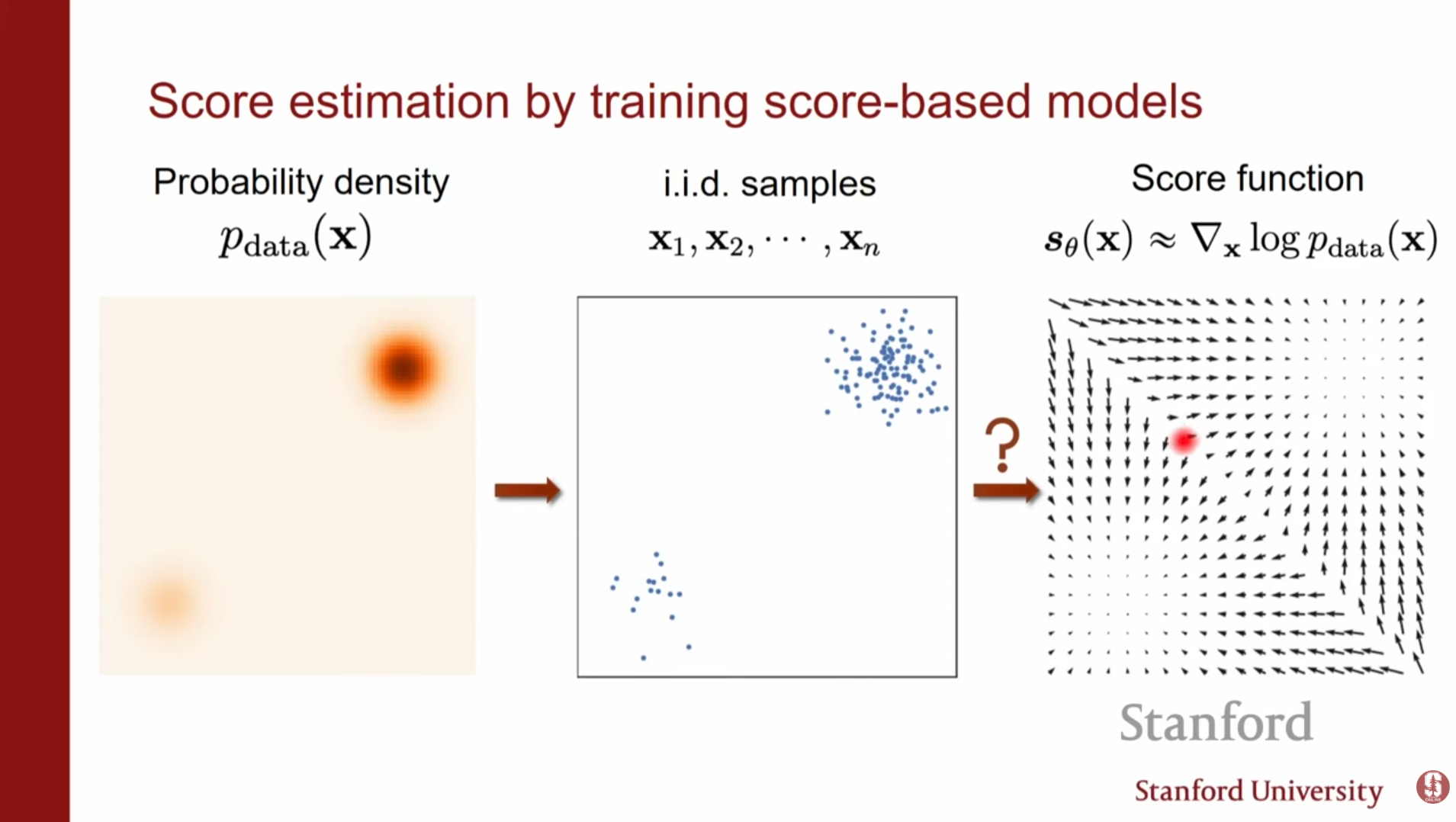
우리는 실제 데이터 분포 $p_{data}(x)$ 를 모르기 때문에, 모델의 스코어 $s_\theta(x)$ 를 데이터의 스코어 $\nabla_x \log p_{data}(x)$ 와 일치시켜야 합니다. 이를 위해 피셔 다이버전스(Fisher Divergence)를 최소화하는 방식을 사용합니다.

기본 스코어 매칭 (Vanilla Score Matching)

초기 목표는 모델 스코어와 데이터 스코어 간의 차이(L2 Norm)를 최소화하는 것입니다.
$\mathcal{L}(\theta) = \mathbb{E}_{p_{data}(x)} \left[ \frac{1}{2} \| s_\theta(x) - \nabla_x \log p_{data}(x) \|_2^2 \right]$
하지만 $\nabla_x \log p_{data}(x)$ 를 알 수 없으므로, 부분 적분(Integration by parts)을 통해 데이터 스코어가 필요 없는 형태로 식을 변형합니다.

변형된 손실 함수:
$\mathbb{E}_{p_{data}(x)} \left[ \text{tr}(\nabla_x s_\theta(x)) + \frac{1}{2} \| s_\theta(x) \|_2^2 \right]$
심화 내용: 계산 복잡도의 문제:
이 방식의 치명적인 단점은 자코비안 행렬의 대각합(Trace of Jacobian), 즉 $\text{tr}(\nabla_x s_\theta(x))$ 을 계산해야 한다는 점입니다. 입력 차원이 $D$ 일 때, 이를 계산하려면 $O(D)$ 번의 역전파(Backpropagation)가 필요하여 고차원 데이터에서는 계산 비용이 매우 비쌉니다.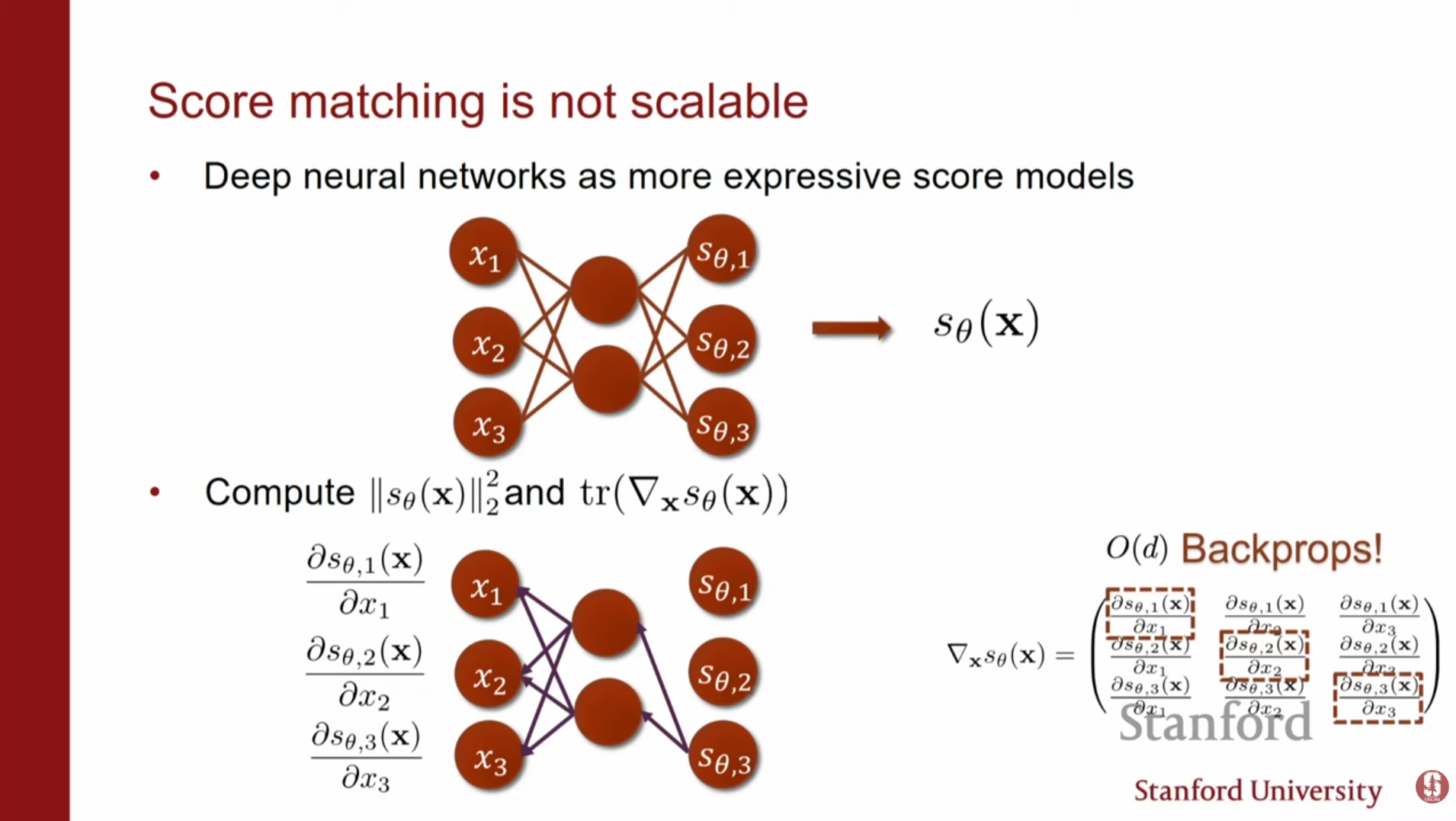

3. 고차원 데이터로의 확장: 효율적인 학습 기법

자코비안 트레이스 계산 문제를 해결하기 위해 두 가지 주요 방법이 소개됩니다.

이해하신 '단발성 노이즈 예측을 통한 스코어 추정'과 'Tweedie's 공식을 통한 DSM의 정당성'을 반영하여, 기존 초안의 흐름을 깨지 않는 선에서 가장 깔끔하게 수정한 버전입니다.

1. 디노이징 스코어 매칭 (Denoising Score Matching, DSM)

데이터에 노이즈를 추가한 분포의 스코어를 추정하는 방식입니다.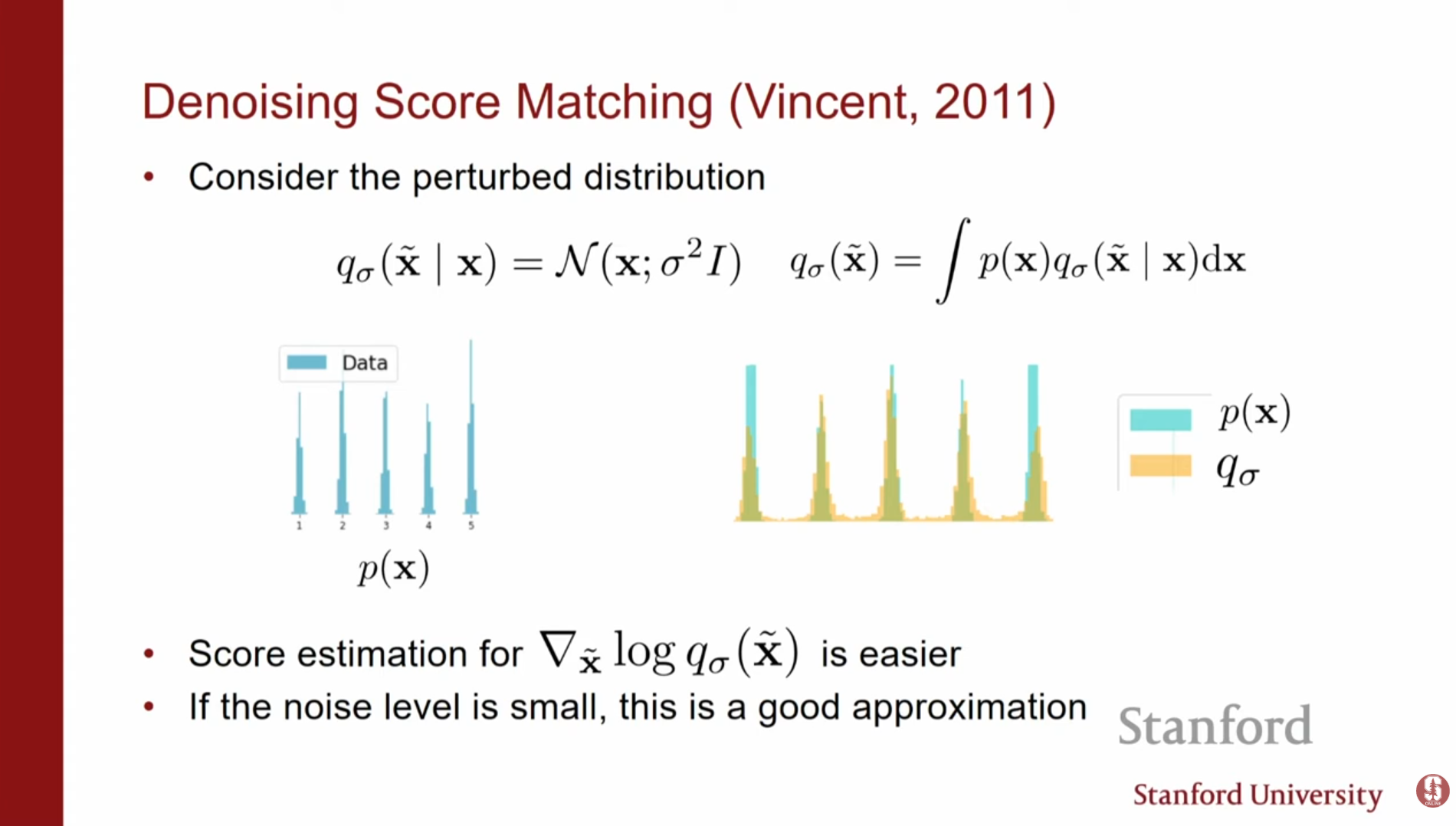

방법: 원본 데이터 에 가우시안 노이즈를 더해 오염된 데이터 $\tilde{x}$ 를 만듭니다 (). 그리고 노이즈가 섞인 데이터 분포 $q_\sigma(\tilde{x})$ 의 스코어를 추정합니다.
수학적 원리: 노이즈가 섞인 데이터에 대한 스코어 매칭 손실 함수는 다음과 같이 단순화됩니다. $\mathcal{L}(\theta) = \mathbb{E}_{q_\sigma(\tilde{x}|x)p_{data}(x)} \left[ \| s_\theta(\tilde{x}) - \nabla_{\tilde{x}} \log q_\sigma(\tilde{x}|x) \|_2^2 \right]$

가우시안 노이즈의 경우, $\nabla_{\tilde{x}} \log q_\sigma(\tilde{x}|x) = \frac{x - \tilde{x}}{\sigma^2}$ 가 되므로, 결국 모델은 더해진 노이즈를 예측(Denoising)하도록 학습됩니다.

핵심 개념: 디퓨전처럼 노이즈를 아주 미세하게 여러 단계로 나누는 것이 아니라, 특정 크기의 노이즈를 한 번에 제거하는 법을 배워 데이터의 스코어(기울기 나침반)를 얻는 단발성 모델링 방식입니다.
장점: 자코비안 트레이스 계산이 필요 없으며, 단순히 노이즈 제거 문제로 귀결되어 계산 효율이 높습니다. 더해진 노이즈를 예측하는 방식은 고화질 이미지 자체를 예측하는 것보다 학습해야 할 범위가 명확하기 때문에 수렴이 훨씬 효율적입니다.

Tweedie's 공식: DSM의 수학적 정당성

Tweedie's 공식은 노이즈가 섞인 데이터에서 원본 데이터를 추정할 때, 왜 단순한 노이즈 예측(DSM)이 스코어 함수를 학습하는 것과 동일한지 수학적으로 뒷받침합니다.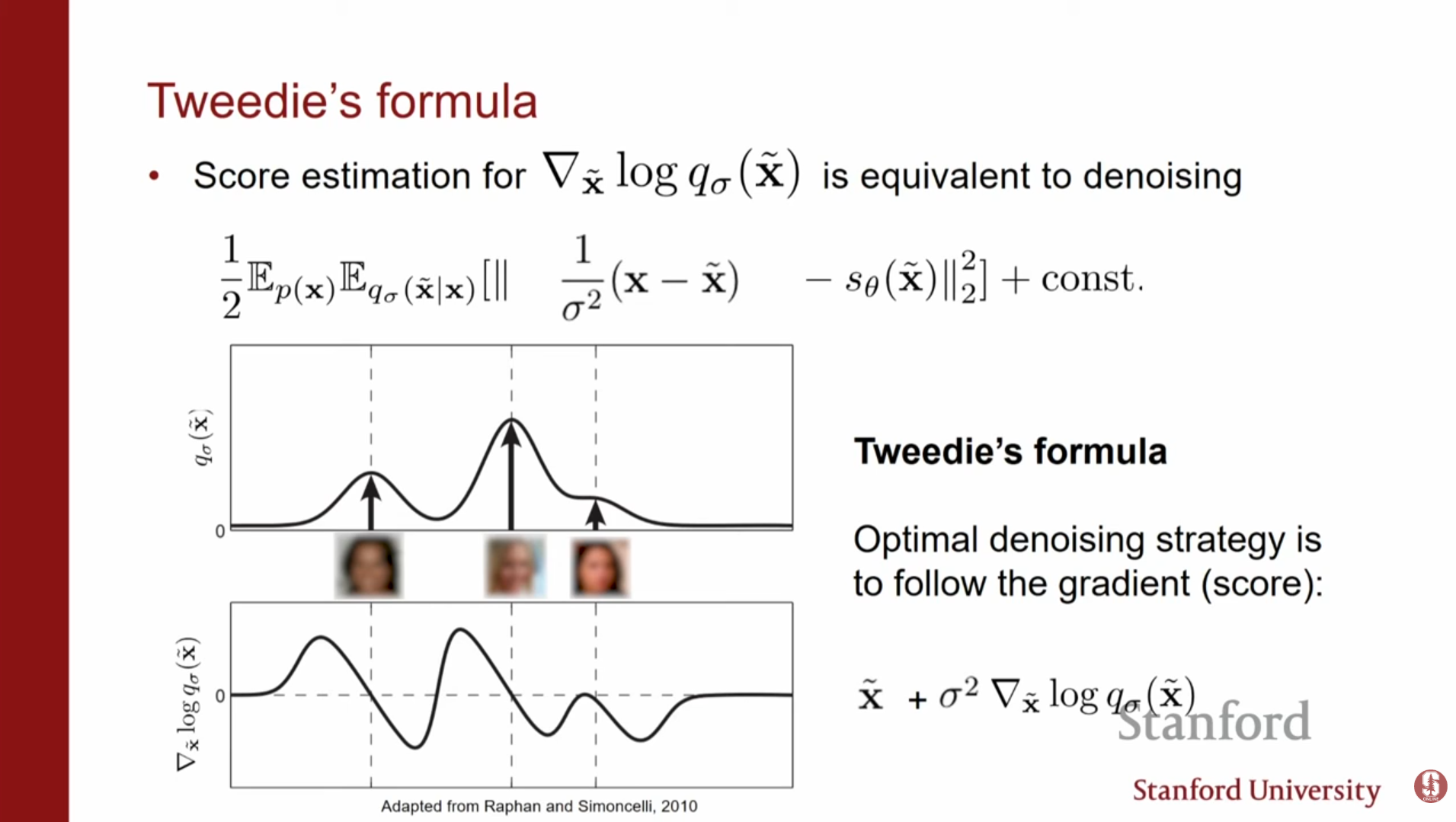

수학적 정의: 가우시안 노이즈가 더해진 관측값 $\tilde{x}$ 가 주어졌을 때, 원본 데이터 의 조건부 기댓값(최적의 복원 지점)은 다음과 같이 표현됩니다.
$\mathbb{E}_{x~p(x|\tilde{x})}[x] = \tilde{x} + \sigma^2 \nabla_{\tilde{x}} \log q_\sigma(\tilde{x})$
DSM과의 연결: 이 공식은 '오염된 데이터( $\tilde{x}$ )에서 스코어( $\nabla_{\tilde{x}} \log q_\sigma$ ) 방향으로 이동하면 원본 데이터의 기댓값에 도달한다'는 것을 보여줍니다. (원본 데이터의 기댓값( $E[x]$ ) = 오염된 데이터( $\tilde{x}$ ) + 스코어방향( $\nabla_{\tilde{x}} \log q_\sigma$ ) x 이동( $\sigma^2$ ))
결론: 모델이 노이즈를 예측하여 제거하도록 학습하는 DSM 방식은, 결국 Tweedie's 공식에 따라 데이터 밀도가 높은 영역으로 향하는 최적의 스코어(방향)를 찾는 과정과 같습니다.

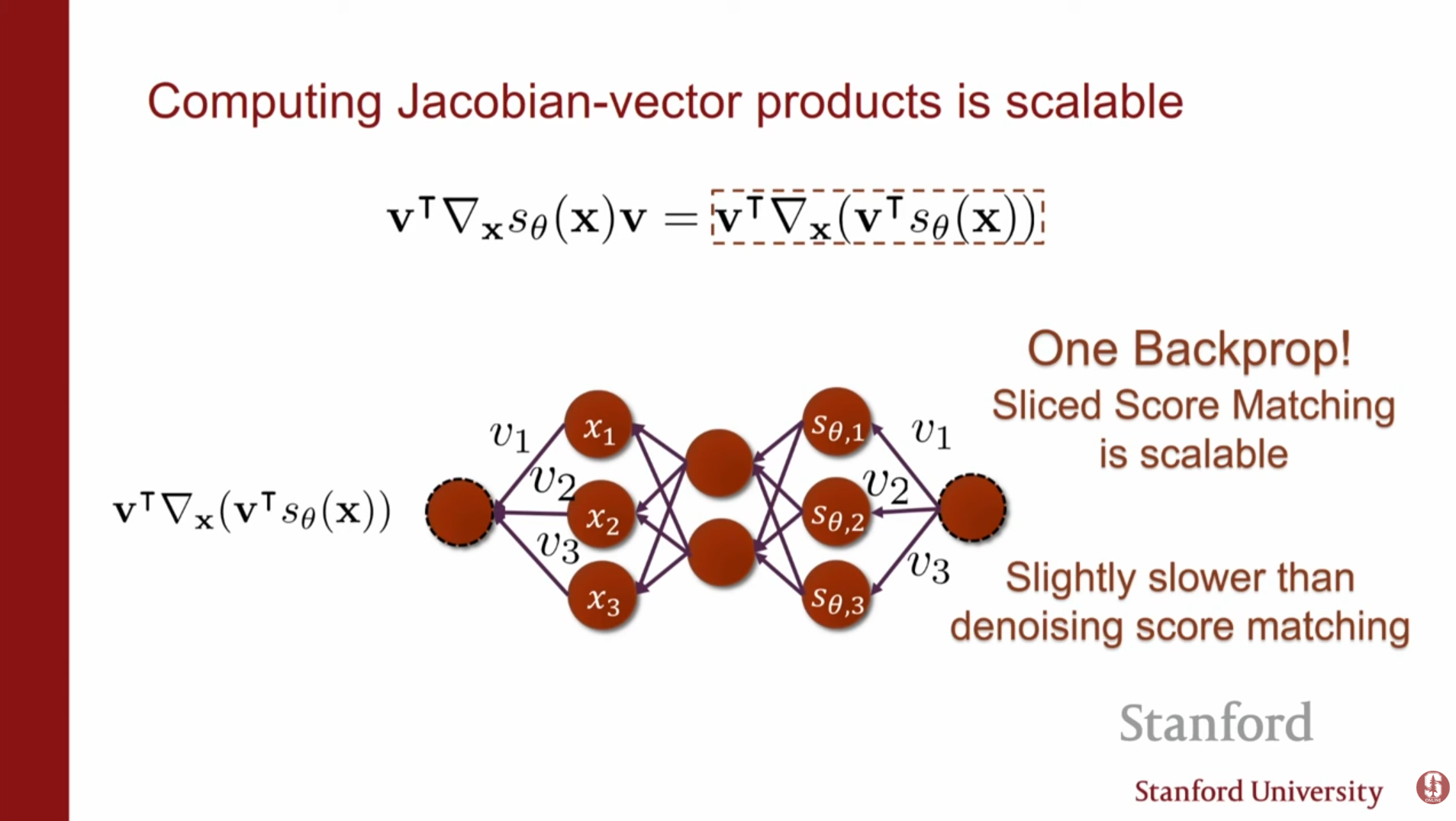
2. 슬라이스 스코어 매칭 (Sliced Score Matching, SSM)

벡터 필드 전체를 비교하는 대신, 임의의 투영 벡터(Projection vector) $v$ 에 사영(Projection)하여 비교하는 방식입니다.

방법: 임의의 방향 $v$ 에 대해 스코어 벡터의 내적값이 일치하도록 학습합니다.
효율성: 자코비안-벡터 곱(Jacobian-Vector product) 형태가 되어, 단 한 번의 역전파로 계산이 가능합니다. 이는 차원 수 $D$ 와 무관하게 일정한 계산 비용을 가집니다.
특징: 투영 방향 $v$ 는 가우시안 분포나 Rademacher 분포에서 랜덤하게 샘플링하며, 이는 원본 스코어 매칭의 비편향 추정량(Unbiased Estimator)이 됩니다.

4. 랑주뱅 역학 (Langevin Dynamics): 샘플링 기법

스코어 함수 $s_\theta(x) \approx \nabla_x \log p(x)$ 를 학습한 후, 어떻게 새로운 데이터를 생성할 수 있을까요? 여기서 랑주뱅 역학(Langevin Dynamics)을 사용합니다. 무작위한 노이즈들이 스코어(기울기) 방향을 따라 흐르도록 유도하여, 모델이 학습한 데이터 분포 내의 이미지를 생성하게 합니다.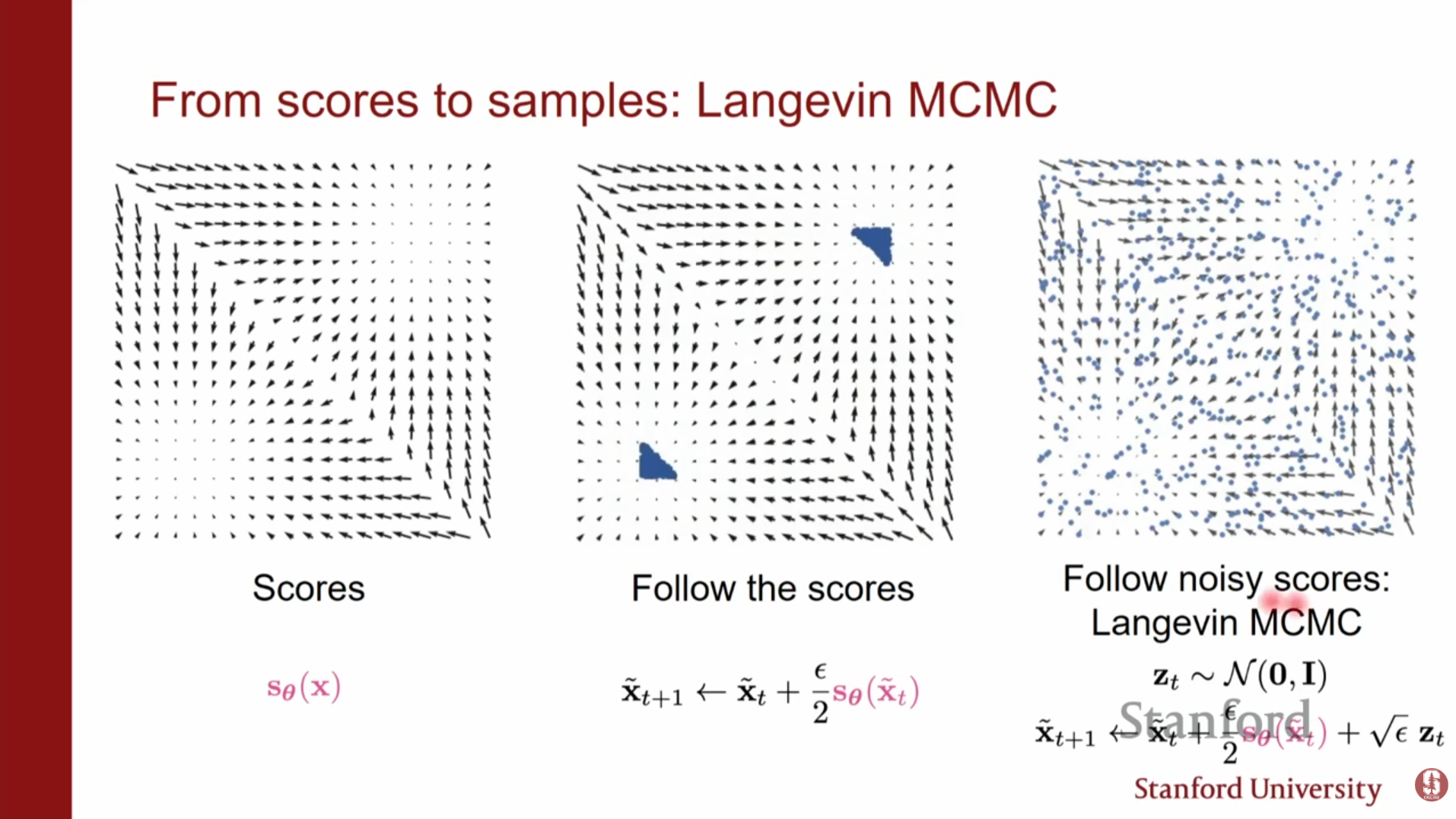

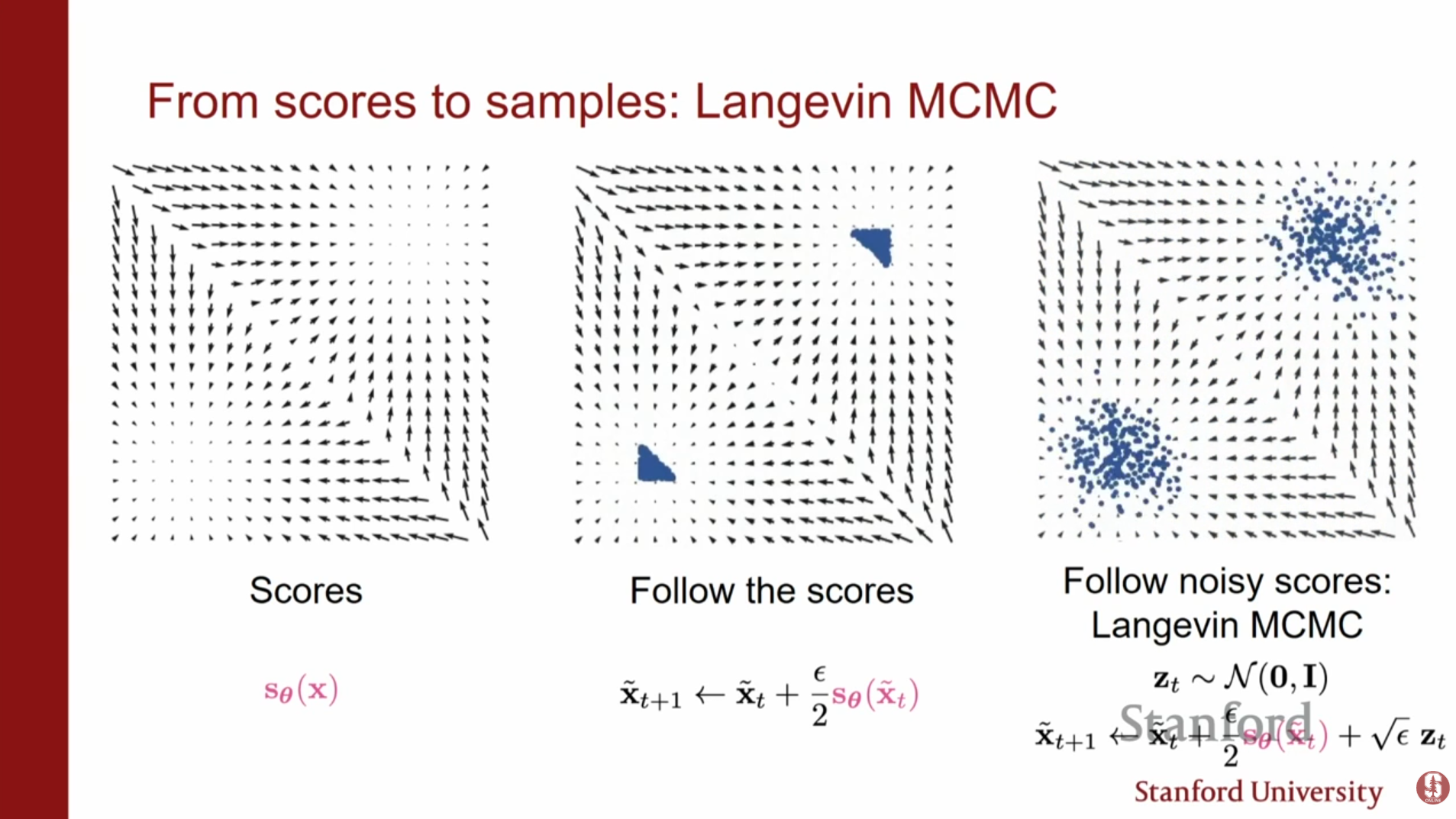
알고리즘: 임의의 노이즈 상태 $x_0$ 에서 시작하여, 스코어가 가리키는 방향(확률 밀도가 높은 방향)으로 이동하되, 적절한 노이즈를 추가하며 반복합니다.
$x_{t} = x_{t-1} + {\epsilon \over 2} \nabla_x \log p(x_{t-1}) + \sqrt{\epsilon} z_t, \quad z_t \sim \mathcal{N}(0, I)$
의미: 스텝 사이즈 $\epsilon \to 0$ 이고 스텝 수 $T \to \infty$ 일 때, 이 과정은 실제 데이터 분포 $p(x)$ 에서 샘플링한 것과 동일해짐이 보장됩니다. 이는 일종의 MCMC(Markov Chain Monte Carlo) 방법입니다.

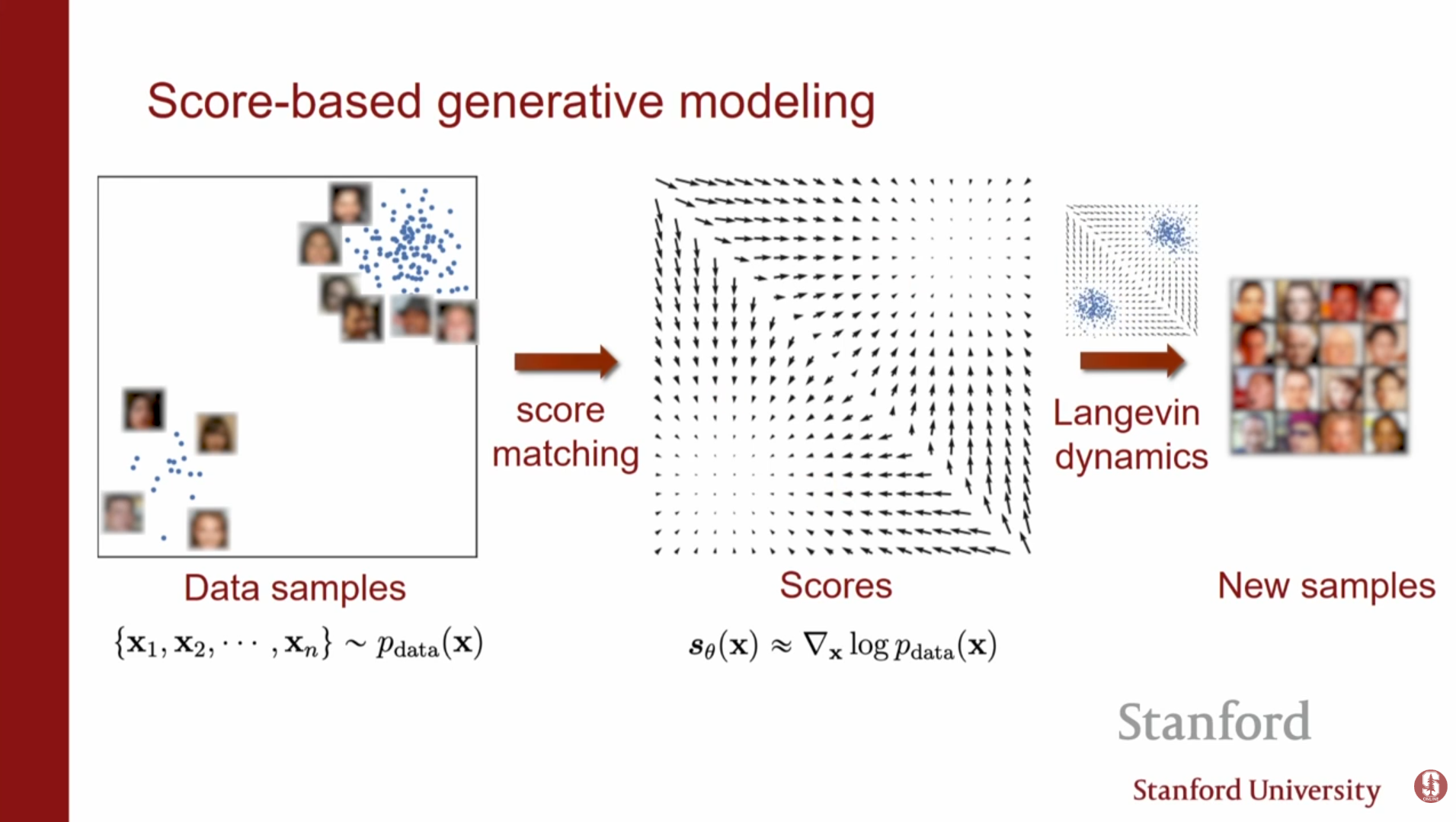
5. 기존 스코어 모델의 한계점

이론적으로는 훌륭하지만, 단순한 스코어 매칭과 랑주뱅 역학을 실제 고차원 데이터(MNIST, CIFAR-10 등)에 적용하면 좋은 결과를 얻지 못합니다. 강의에서는 세 가지 주요 원인을 지적합니다.

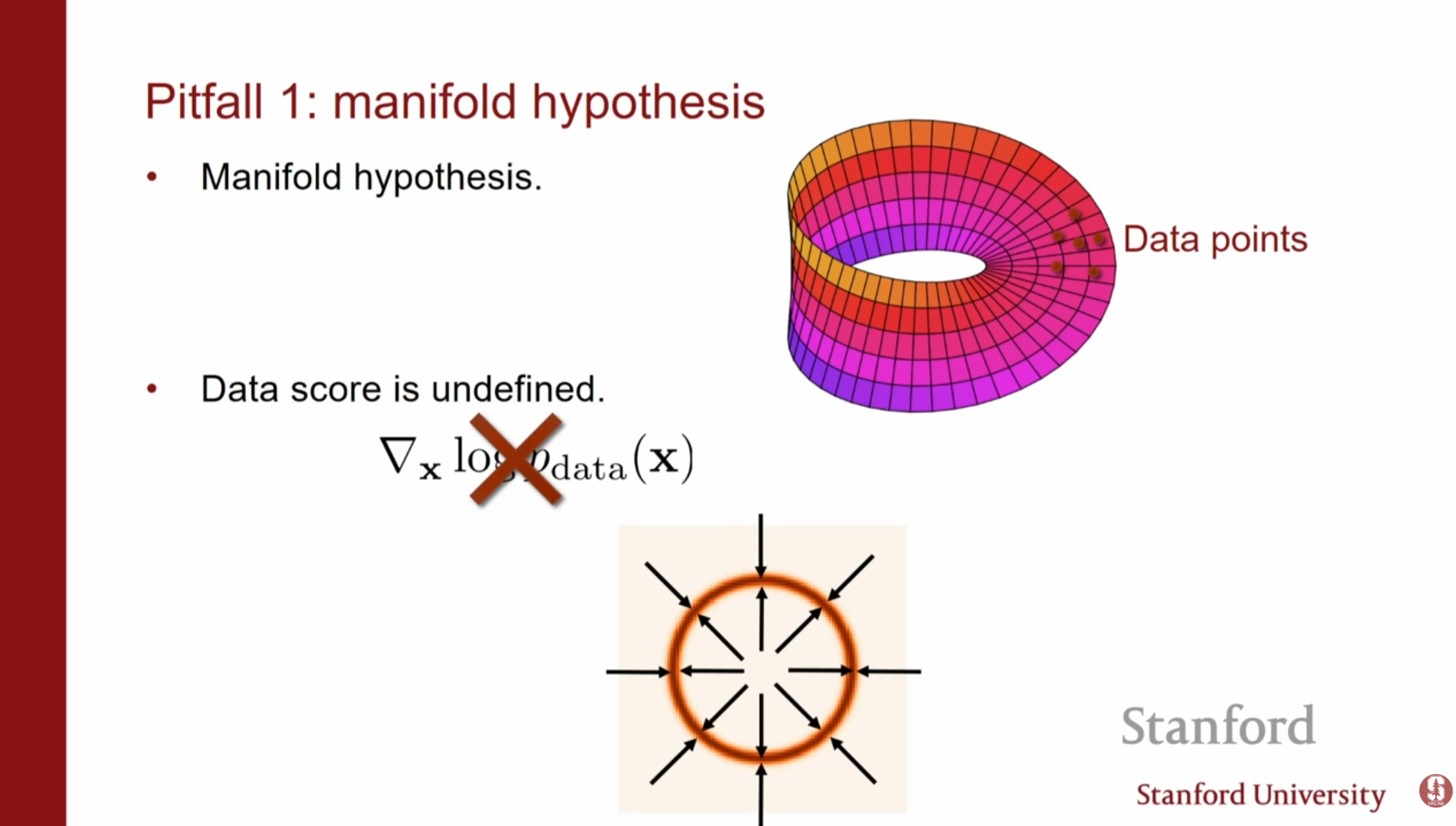
1. 다양체 가설 (Manifold Hypothesis)

실제 데이터는 고차원 공간(Ambient space) 전체에 퍼져 있지 않고, 훨씬 낮은 차원의 다양체(Manifold) 위에 존재합니다. 예를 들어, CIFAR-10 이미지를 PCA로 분석해보면 차원을 크게 줄여도 정보 손실이 거의 없습니다.

문제점: 데이터가 존재하지 않는 공간에서는 스코어(기울기)가 정의되지 않거나 발산할 수 있습니다.

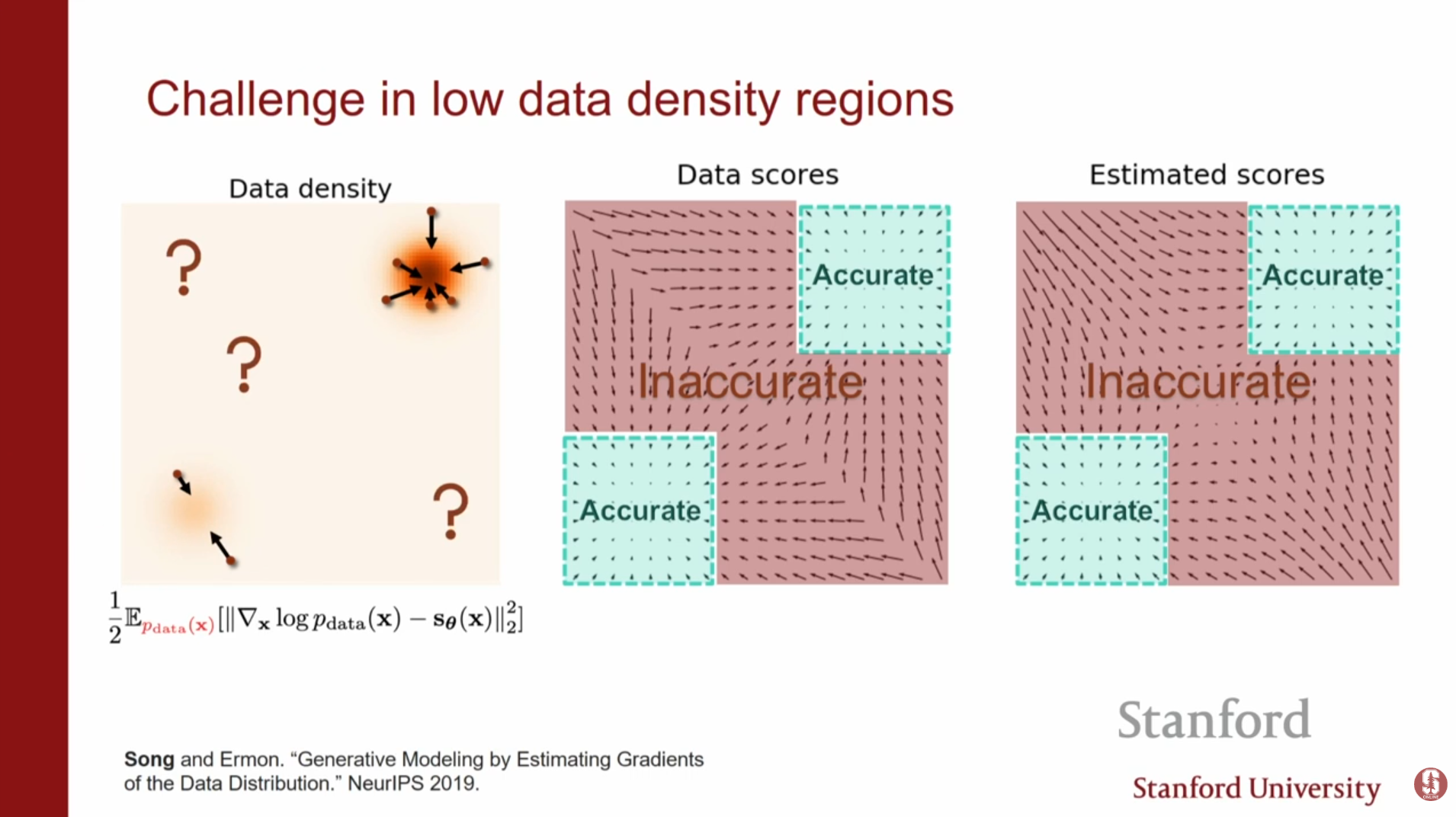
2. 낮은 데이터 밀도 영역 (Low Data Density Regions)

스코어 매칭은 데이터가 있는 곳( $p_{data}(x)$ 가 높은 곳)에서만 정확한 스코어를 추정하도록 학습됩니다.

문제점: 랑주뱅 역학을 수행할 때, 초기 샘플은 데이터가 없는 낮은 밀도 영역에서 시작됩니다. 이 영역에서는 스코어 추정이 부정확하므로, 샘플링 경로가 엉뚱한 방향으로 흘러가게 됩니다.

3. 느린 혼합 (Slow Mixing)

데이터 분포가 서로 떨어진 여러 개의 모드(Mode)를 가질 때(예: $p(x) = \pi p_1(x) + (1-\pi) p_2(x)$ ), 스코어 함수는 각 모드 간의 상대적 가중치 $\pi$ 에 대한 정보를 잃어버립니다.

심화 내용: 로그를 취하고 미분하면 상수항이 사라지기 때문에, $\nabla_x \log p(x)$ 는 각 모드 내부의 모양만 알 수 있을 뿐, 모드 간의 이동이나 전체적인 비율을 반영하지 못합니다. 결과적으로 샘플링 시 실제 비율대로 샘플이 생성되지 않고 특정 모드에 갇히는 문제가 발생합니다.

6. 강의 QnA 요약

Q1: 왜 '기울기(Gradient)'라고 부르지 않고 '스코어(Score)'라고 부릅나요?
A1: 문헌에서 통상적으로 사용되는 용어이며, 특히 스코어 매칭 손실 함수와 관련하여 '피셔 스코어(Fisher Score)'라는 용어가 사용되기 때문입니다. 의미적으로는 로그 우도의 기울기와 같습니다.

Q2: 디노이징 스코어 매칭(DSM)에서 반드시 가우시안 노이즈만 사용해야 합니까?
A2: 아닙니다. 노이즈 분포의 기울기를 계산할 수 있고 닫힌 형태(closed form)로 표현 가능하다면 다른 분포도 사용할 수 있습니다. 다만, 가우시안 노이즈가 수학적으로 다루기 가장 편리합니다.

Q3: 슬라이스 스코어 매칭(SSM)에서 투영 벡터를 랜덤하게 선택하면 정보 손실이나 편향이 생기지 않습니까?
A3: 랜덤 투영은 원본 손실 함수의 비편향 추정량(Unbiased Estimator)이므로 이론적으로 문제가 없습니다. 분산을 줄이기 위해 여러 벡터를 사용하여 평균을 낼 수도 있지만, 실제로는 하나의 벡터만 사용해도 잘 작동합니다.

7. 핵심 내용 요약

스코어 기반 모델의 정의: 확률 밀도 함수를 직접 모델링하는 대신, 로그 우도의 기울기(스코어)를 모델링함으로써 정규화 상수의 제약을 피하고 다양한 신경망 구조를 활용할 수 있습니다.
효율적인 학습 방법: 기본 스코어 매칭의 계산 비용 문제를 해결하기 위해 디노이징 스코어 매칭(DSM)과 슬라이스 스코어 매칭(SSM)이 제안되었습니다. 특히 DSM은 생성 문제를 '노이즈 제거(Denoising)' 문제로 변환하여 효율성을 높였습니다.
한계와 발전 방향: 다양체 가설, 데이터 희소 영역에서의 부정확한 스코어 추정, 느린 혼합 문제 등으로 인해 초기 모델은 고해상도 이미지 생성에 실패했습니다. 이러한 문제를 해결하기 위해 노이즈 레벨을 조절하며 샘플링하는 방식이 연구되었으며, 이는 확산 모델(Diffusion Models)로 발전하는 기초가 됩니다.

김성윤(Jack)

AI 공부합니다

이전 포스트

[CV] CS236 12강 정리 [Energy Based Models]

다음 포스트