[논문 리뷰] Hierarchical Graph Representation Learning with Differentiable Pooling

논문 링크 : Hierarchical Graph Representation Learning with Differentiable Pooling

1. 선택하게 된 이유

: 그래프 관련해서 기본 지식들을 탑재하고자 state-of-the-art의 코드가 많은 순서대로 공부하던 중 관심이 생겼습니다.

2. 서론 :

• 최근 GNN은 노드 임베딩을 학습하고 node classification과 link prediction을 한다.
• 하지만, 최근 GNN 방법은 inherently 'flat'(only propagte information across the adges of the graph)이고 'hierarcihical' representation을 학습하지 않는다.
• 기존의 graph classification을 적용할 때는 모든 노드에 대한 임베딩을 만들고, 모든 노드에 대해 'globally pool' 적용했다.
• 이는 hierarchical structure을 무시하고, 그래프 전체를 예측하는 일을 어렵게 한다.
• GNN의 도전과제가 graph는 no natural notion of spatial locality이기 때문에 어떻게 노드 간 cluster를 하는지 학습이 필요한데, 이를 위해, hierarchical structure를 만드는게 필요하다.
• DIFFPOOL은 differentiable graph pooling module이다. 그리고, hierarchical representations of graphs을 만들어 내고, end-to-end fashion에서 다양한 GNN 구조와 합쳐진다.
• DIFFPOOL은 GNN 각 층에서 노드에 대한 differentiable soft cluster assignment를 학습한다.

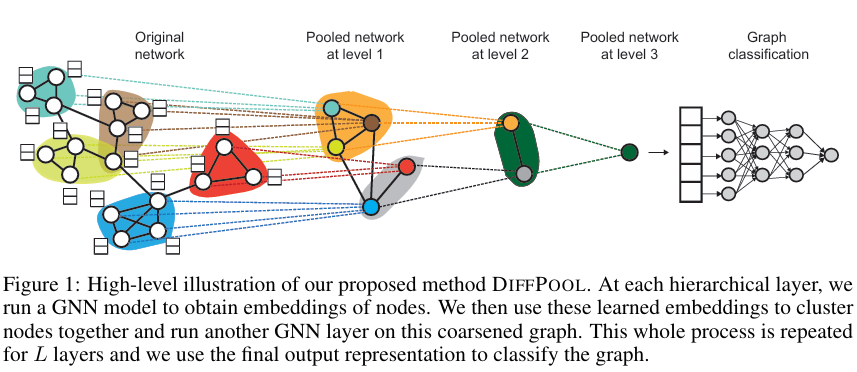
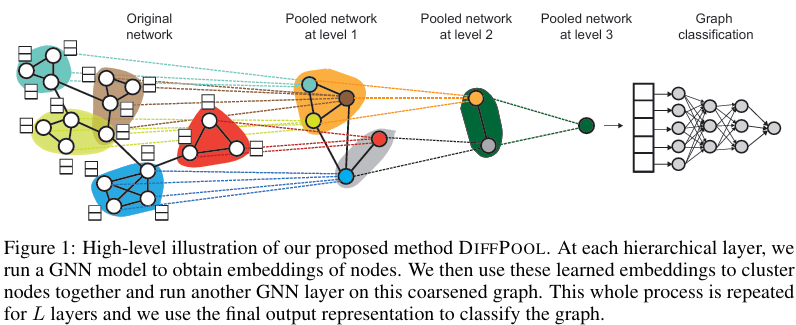
• 위 그림처럼 hierarchical 'stacking' GNN layers을 적용한다.
• 위 그림을 해석하자면, 여러 노드들이 cluster되면, 그 cluster가 다음 level(이후 등장하는 layer)에서 새로운 노드로 작용하고, 재귀적으로 하나의 노드만 남도록 작동하는 느낌이다.
• 일반적인 GNN에 대한 접근은 GNN을 message passing algorithm으로 보는 것이다.
• message passing algorithm은 node representatios이 순차적으로 인접노드들의 특징으로부터 differentiable aggregation function을 통해 계산되는 것이다.
• 최근 Graph wclassification 에서의 도전과제는 GNN을 노드 임베딩에서 그래프 전체를 표현하는데 적용하는 것으로 이동한다.
• 최근 hierarchical graph respresentations을 학습하는 연구가 있었지만, 이 논문은 hierarchical structure을 학습한다는 점에서 다르다.

3. 방법론 : Proposed Method

3-1. Preliminaries

• 기본 수식 정의 :

  Graph $G = (A,F), \space where \space A \in \{0,1\}^{n \times n}, \space G_i \in G$
  Node feature matrix $F \in \R^{n \times d},$ each node has d features
  Labeled graphs $D = \{(G_1,y_1),(G_2,y_2),...\} \space where \space y_i \in Y$

• Graph $G_i$에서 $y_i$를 예측하는 것이 graph classification의 목표다.
• input graphs에서 유용한 feature vectors을 뽑아내는 것이 목표다.
• 분류 문제에 ML methods를 적용하기 위해 각 그래프를 유한한 차원의 벡터로 바꾸는 과정이 필요하다.

GNN

• end-to-end fashion에서 그래프 분류의 useful representations을 학습하기 위해 GNN을 만들었다.

  Equation 1
  $H^{(k)} = M(A,H^{(k-1)};\theta^{(k)}$

• GNN으로 genral "message-passing" architecture인 (Equation 1)로 정했다.
• (Equation 1)에 쓰이는 수식에 대한 설명 $H$는 GNN을 $k$번 거쳐서 계산된 노드 임베딩들이다. $M$은 message propagation function이다. $A$는 adjacency matrix이다. 세타는 학습가능한 파라미터이다. $H^{(0)}$은 $F$으로 설정한다.
• 결국 (Equation 1)이 GNN의 학습 한번의 과정을 보여주는 것이다.
• 여기서 쓰이는 GNN 모델과 $M$은 어떤 것음 사용해도 상관 없다.
• $Z$는 final output node embeddings으로 GNN이 정해진 $k$번 만큼의 과정을 거치고 나오는 마지막 output이다. (K번의 과정을 거치는 것이 1 layer에서의 과정이다.)
• 이것을 아래와 같이 나타내겠다.

  $Z= GNN(A, X)$

Stacking GNNs and pooling layers

• 위에서 말했듯이, $k$번의 학습을 거친 GNN이 하나의 layer를 담당하고, 이를 총 $l$번 반복하면 $l$ GNN layers가 되고, GNN을 stack하게 된다.
• 그러므로 GNN의 output인 노드들을 어떻게 cluster or pool하는지 학습하는 것이 목표다.
• 그리고 이러한 GNN을 위한 pooling layer을 만들기 위해 hierarchically pool nodes를 하는 general한 방법을 제시하는 것이 목표다.

3-2. Differentiable Pooling via Learned Assignments

• 그래프 분류를 잘하기 위한 노드 임베딩 추출과 hierarchical pooling을 잘하기 위한 노드 임베딩 추출을 위해 GNN을 사용할 것이다.
• 3-1.에서 말한 방식으로 GNN을 사용하므로서 GNNs in DIFFPOOL은 general pooling strategy를 encode하는 것을 학습할 수 있다.
• 앞으로 아래 2가지에 대해서 말하겠다.

  1. how the DIFFPOOL module pools nodes at each layer given an assignment matrix.
  2. how we generate the assignment matrix using a GNN architecture.

Pooling with an assignment matrix

• $S^{(l)}$은 learned cluster assignment matrix at layer $l$이다. $S^{(l)}$의 row는 layer $l$에서의 nodes에 해당하고, column은 layer $l+1$에서의 clusters에 해당한다. (쉽게 말해, 어떤 노드가 어떤 cluster에 들어가야하는지에 대한 확률 지표이다.) $S^{(l)}$ soft assignment로 제시된다. (여기서 soft하다는 것은 softmax의 soft처럼 0과 1이 아닌 그 사이의 연속값으로 표현된다는 의미같다.)

  Equation 3
  $X^{(l+1)} = S^{(l)^T} Z^{(l)} \in \R^{n_{l+1} \times d}$
  
  Eqaution 4
  $A^{(l+1)} = S^{(l)^T} A^{(l)} S^{(l)} \in \R^{n_{l+1} \times n_{l+1}}$

• $S^{(l)}$이 계산되었다고 가정했을 때, (뒤에서$S^{(l)}$계산하는법 나온다.) $A^{(l)}$은 layer $l$에서 adjacency matrix (쉽게 말해, 노드들의 연결 관계를 나타내는 행렬). $Z^{(l)}$은 layer $l$에서 input node embedding matrix이다. (위에서 말했듯이$Z$는$k$번의 GNN을 거친 최종 임베딩 행렬이다. 임베딩 행렬은 보통 nodes의 feature에 대한 정보를 담고 있다.)

• (Equation 3, 4)를 통해서 다음 layer에서 사용될 embedding matrix X와 agjacency matrix A가 만들어진다.

• (Equation 4)에서 $A^{(l)}$은 $S^{(l)}$과 행렬연산을 거치기 때문에, $A^{(l+1)}$은 그래프 연결 상태를 나타내지만, 연결 상태의 가중치 정도도 표현된다. 이를 통해, connectivity의 strength을 반영하고 있다. $X^{(l+1)}$ 역시 같은 원리로 가중치가 부여된다.

Learning the assignment matrix

Equation 5
$Z^{(l)} = GNN_{l,embed} (A^{(l)}, X^{(l)})$

Equation 6
$S^{(l)} = softmax \big (GNN_{l,pool}(A^{(l)},X^{(l)}) \big )$

• 위에서 사용했다. $Z^{(l)}$과 $S^{(l)}$은 (Equation 5, 6)을 통해서 계산됐다.
• (Equation 5)는 위에서 설명한 구조를 수식으로 나타낸 것이다.
• (Equation 6)에서 softmax 함수는 row 단위로 적용한다. 그리고, pooling GNN의 output 차원은 hyperparameter인 layer L의 최대 군집 수로 한다.
• embedding GNN과 pooling GNN은 같은 input을 넣지만, embedding GNN은 input nodes에 대한 새로운 embeddings을 만들어내도록 학습하고, pooling GNN은 input nodes를 cluster로 확률적으로 할당하는 행렬을 만들어내도록 학습한다.
• 맨 처음의 adjacency matrix A와 node features F는 original graph로부터의 행렬들로 한다. 그리고, 마지막 layer는 하나의 cluster만을 가지도록 한다. 이 cluster는 differentiable classifier의 input으로 사용된다. 추가적으로, 이 모든 시스템은 stochastic gradient descent를 사용한 end-to-end로 학습된다.

Permutation invariance

• useful for graph classification을 위해 the pooling layer은 노드 순열(permutation)에 대해 불변(invariance)해야한다. 이는 DIFFPOOL의 기반이 되는 어떤 GNN이 permutation invariant하면 된다.

  Proposition 1.
  Let $P \in \{0,1\}^{n \times n}$ be any permutation matrix,
  then $\small DIFFPOOL(A,Z) = DIFFPOOL(PAP^T,PX)$
  as long as $\small GNN(A,X) = GNN(PAP^T, X)$
  (i.e. as long as the GNN method used is permutation invariant).

• 그래서 (Proposition 1)처럼 permutation invariant한 GNN을 쓰면 된다.

• 따라서 (Equation 5, 6)은 GNN이 permutation invariant하다는 점에서 증명되고, (Equation 3, 4)는 모든 permutation matrix는 orhogonal 하다는 점을 통해서 $P^T P = I$ 수식을 적용하면 증명된다. (Equation 4도 순열 불변성을 위해서 수식이 그렇게 구성되었다고 보면 된다.)

• 증명에 대한 개인적인 생각은 이렇다. DIFFPOOL의 과정에서 쓰이는 $S^{(l)}$과 $Z^{(l)}$는 결국 GNN에서 나오는데, GNN이 permutation invariant이면, GNN에 들어가는 A와 X가 variant해져도 결과는 invariant될 것이고, 결국 DIFFPOOL은 invariant한 $S^{(l)}$과 $Z^{(l)}$을 사용하게 되니, (Equation 3)는 해결. (Equation 4)에서 문제가 되는 $A$는 앞 뒤에 $S$와 $S^T$이 곱해지면서 정규 직교 행렬 사이에 존재하게 되었고, 이는 순서와 상관없이 같은 벡터를 내놓기 때문에 증명된다. (+ 정규 직교 행렬 사이의 곱은 어떤 항상 같은 공간 내의 같은 벡터를 내놓는다. 순열행렬이 가해져서 순서가 변한다$(A => P A P^T)$고 해도 값은 유지되는데, 정규 직교 행렬인$(S, S^T)$사이에 행렬($P A P^T => S P A P^T S^T)$의 순서와 상관없이 동일한 벡터를 나타낸다는 특징으로 증명이 된다.)

3-3. Auxiliary Link Prediction Objective and Entropy Regularization

• (Equation 4)로 pooling GNN을 학습할 때는 오직 gradient signal만으로는 non-convex 최적화 문제에서 local minima에 빠질 수 있다. 그래서 auxiliary link prediction objective (쉽게 말해, 주변 노드를 함께 풀링하도록 하는 장치)를 학습할 때 이용한다.
  특히,

  $L_{LP} = ||A^{(l)},S^{(l)}S^{(l)^T}||_F,$ where $|| \cdot ||_F$ denotes the Frobenius norm

  이 최소화 되도록 한다. 이렇게 하면, $A^{(l)}$ 행렬은 low level의 행렬이 된다.

• pooling GNN의 또다른 특징은 output cluster가 one-hot vector에 가까워야 한다.(왜냐하면 하나의 군집에 속하도록 해야하니까) 그러므로,

  $L_E = {1 \over n} \sum^n_{i=1} H(S_i),$ where H denotes the entropy function, and S_i is the i-th row of S.

  과 같이 $S^{(l)}$의 row들의 cluster entropy의 평균을 최소화하도로고 규제해서 이를 해결한다.

4. 주요 결과 :

4-1. Baseline Methods

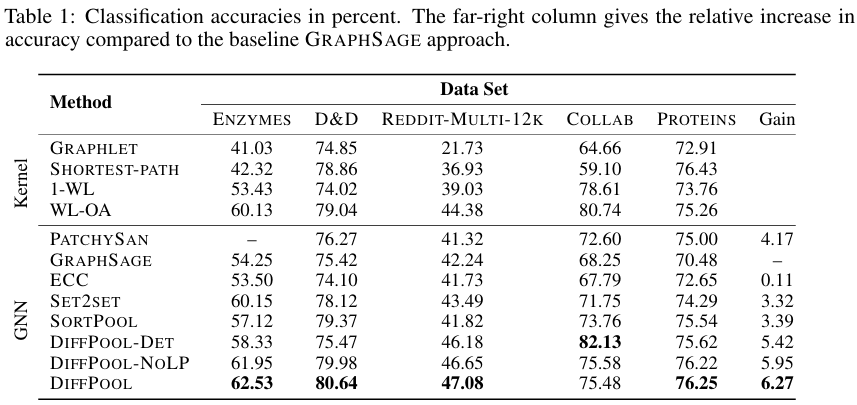
• 다른 기법들과 성능비교 결과이다.

4-2. Results for Graph Classification

• (Table 1)의 결과는 Q1과 Q2에 대한 좋은 답변이다. DIFFPOOL-DET이 성능이 좋은 경우가 있었는데, 이건 데이터 셋이 single-layer community structures만 나타내기 때문이다. 추가적으로 관찰된 점은 조건이 똑같은 환경에서도 결과가 다를 정도로 학습이 불안정하다는 점이었는데, 이는 link prediction objective를 통해서 보완했다.

• DIFFPOOL은 다른 GNN 구조에도 적용될 수 있어서 S2V(Structure2Vec)을 활용해서 실험해봤다.
  

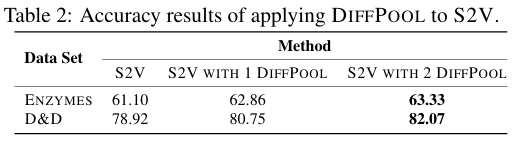
• 아래는 S2V와 DIFFPOOL을 층별로 어떻게 섞었는 지를 나타내는 구조다.

• S2V with 1 DIFFPOOL = S2V_layer=1 | DIFFPOOL_1 | S2V_layer=2 | S2V_layer=3

• S2V with 2 DIFFPOOL = S2V_layer=1 | DIFFPOOL_1 | S2V_layer=2 | DIFFPOOL_2 | S2V_layer=3

• (Table 2)에서 결과를 혹인 할 수 있듯이, DIFFPOOL은 GNN 구조에 이점을 제공하는 일반적인 구조임을 확인할 수 있다.

• DIFFPOOL은 추가적으로 많은 running time을 가져오지 않는다. 왜냐하면, DIFFPOOL은 그래프 사이즈를 축소 시키고 이는 다음 layer에서 속도를 높이기 때문이다. 실제로 SET2SET을 사용한 GRAPHSAGE model보다 12배 빠르다.

4-3. Analysis of Cluster Assignment in DIFFPOOL

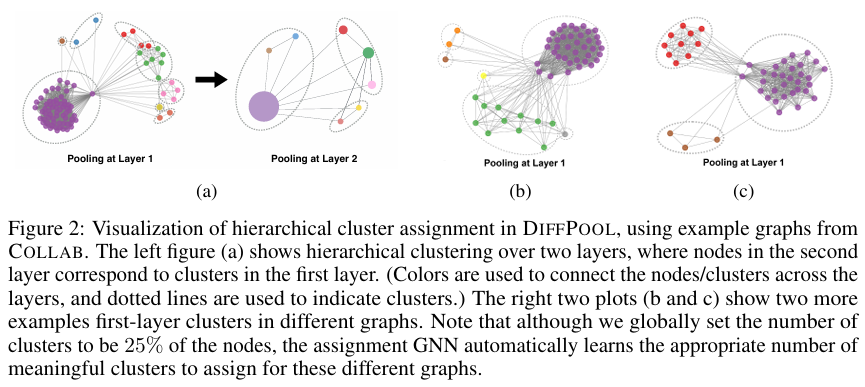
• (Figure 2a)를 통해서 실제로 군집화를 잘 이루어내고 있음을 확인할 수 있다.
• Dense subgraph structure에 비해 sparse subgraph structure은 다양한 구조들 때문에 GNN message-passing이 이 구조를 잡아내는데 실패할 수 있다. 그래서 subgraph 특정 부분 개별적으로 풀링하면서 의미있는 구조를 뽑아내는 것을 학습할 수 있다.
• assignment network은 soft cluster assignment을 input nodes의 feature과 그들의 이웃에 기반하여 계산하기 때문에 input feature와 neighborhood structure이 비슷한 노드들은 비슷한 cluster assignment가 되어야 하는데, pooling network는 실제 결과로 그렇다는 것을 확인했다.
  -Pre-defined Maximum Number of Clusters(C)은 hyperparameter인데, 이 수치에 민감하게 성능이 변하는 것을 파악할 수 있다. 그래서 풀링층은 적절한 수치를 쓰는 것을 학습해야한다. 특히, 몇몇의 cluster은 사용되지 않을 수 있다. (Figure 2c)처럼 만약 hyperparameter C가 5인데, cluster 3개로 충분히 군집을 이루면, 2개의 cluster가 남는다.

5. Comment
: 일반적인 흐름에서 벗어서 새로운 패러다임을 제시한다는 점이 인상적이었다. 그래프와 재귀적인 개념, pooling 개념을 종합적으로 섞었다는 점이 신기했다. 평소에 섞어서 생각해보지 못한 내용들로 혁신을 만들어 낸다는 것이 신기하고 도전하고 싶어졌다. 추가적으로, 논문을 읽으면 읽을수록, 수학적인 내용을 반드시 의미적으로 이해해야하는 부분들이 많이 나오고, 이는 선형대수에 대한 깊은 이해와 지식이 반드시 필요하다는 것을 느낀다.

더 자세한 내용은 논문 원본을 참고하시기 바랍니다.

개인의 주관이 반영된 해석이라 논문의 의도와 다를 수 있습니다. 
오류가 있다면 댓글로 알려주시면 감사하겠습니다!