[논문 리뷰] SuperGlue : Learning Feature Matching with Graph Neural Networks

논문 링크 : SuperGlue : Learning Feature Matching with Graph Neural Networks

1. 선택하게 된 이유

: GNN이라는 기술에 관심이 생겨서 논문을 읽어보려고 하는데, 최신 기술 중 가장 구현이 많이 된 논문이라서 선택하게 됐습니다.

2. 서론

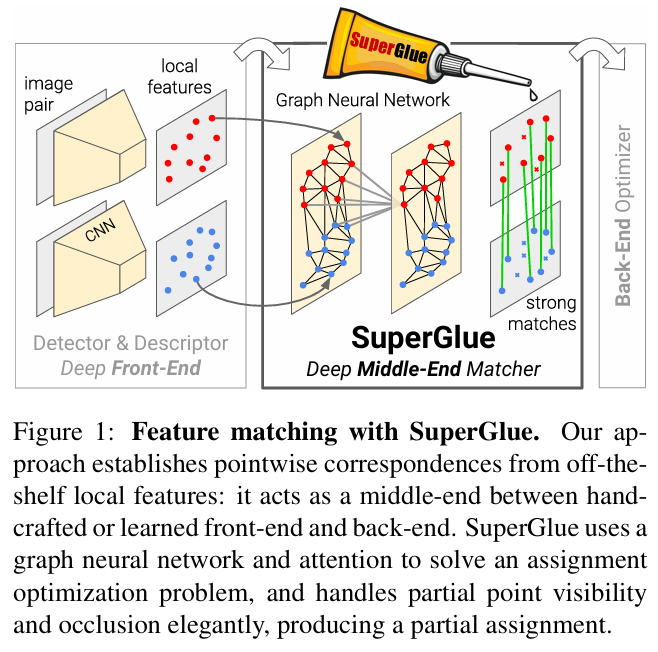
• SuperGlue는 두 개의 local features를 연결하는 neural network이다.
• GNN으로 pre-existing local features로부터 matching process를 학습하고 얻은 cost을 바탕으로 differentiable optimal transport problem의 해결하는데 활용한다. 이때, Sinkhorn algorithm을 활용한다. 이를 통해 두 개의 local features 사이의 the partial assignment 찾는다.
• Attention 기술을 통해 flexible context aggregation mechanism을 제시한다. 그리고 self-attention (같은 이미지에서) 와 cross-attention (다른 이미지에서) 을 사용해서 공간적 정보(spatial relationships of the keypoints, 예를 들면, 좌표값)와 시각적 정보(visual appearance, 예를 들면, RGB 값)를 모두 활용한다.

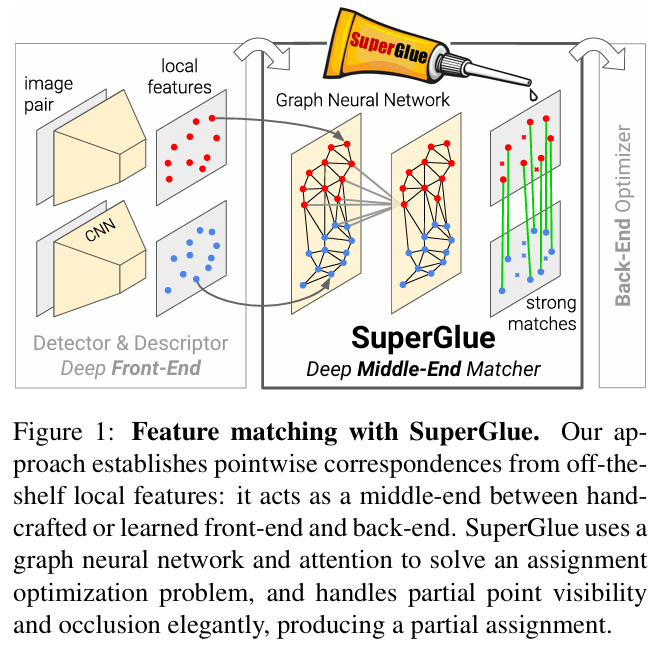
• SuperGlue는 visual feature extraction의 front-end 와 bundle adjustment or pose estimation의 back-end 사이의 middle end 단계에서의 기술이다.
• 기존 기술들은 NN Search(오직 노드 간 거리 기반)에 의해 추정하며, the assignment structure과 visual information을 무시한다.
• Self-attention을 Message Passing Graph Neural Network on a complete graph의 한 예로 볼 수 있음에서 아이디어가 시작했다.

3. 방법론 : The SuperGlue Architecture

Motivation

• 3D world의 특징을 반영하기 위해 2가지 제약 조건을 건다.

  1) keypoint은 최대 한 쌍만 이룰 수 있다.
  2) 몇몇의 keypoints은 occlusion & failure of the detector 문제로 매칭이 안될 수 있다.

• 앞으로 할 일이 3D world에서 특정 두 순간인 2D image들 간의 keypoints matching 성능을 높이기 위한 일인 것을 염두해두자.

Formulation

1. local features은 $(p, d)$로 표현 ($p$는 keypoints의 positions을 나타내고, $d$는 visual descriptors을 나타낸다.)
2. $P_i$ $:= (x, y, c)_i$ (x, y는 이미지 좌표값, c는 인식 확신 정도값)
3. $d_i$ 는 SIFT나 SuperPoint 기법을 통해 추출한 값
4. $A$와 $B$는 $M, N$의 index를 가진다.

Partial Assignment

• 두 keypoints간 matching을 위해 필요한 $P$(Partial Assignment)를 다음 식과 같이 정의함.

Equation 1
$P1_N \leq 1_M$ and $P^T1_M \leq 1_N$

• 최종 목표는 neural network 학습을 통해 두 keypoints 사이의 partial assignment를 예측하는 것이다.

3-1. Attentional Graph Neural Network

• local features이외에도 문맥적 내용 (attention, 많은 특징을 모아서 서로의 관계성에 대해 학습) 논리를 통한 애매모호함을 제거할 수 있다.

Keypoint Encoder

Equation 2
$^{(0)}$$x_i$ $=$ $d_i$ $+$ $MLP_{enc}$ $(p_i)$.

• (Equation 2)와 같이 keypoint의 visual appearance와 location을 임베딩한다.
  이는 NLP에서의 'posional encoder'와 유사하다.

Multiplex Graph Neural Network

• 두 images의 keypoints에 대한 complete graph를 위한 두 가지 edge를 제시한다.

1) Intra-image edges : 같은 이미지 내에서 keypoints 간의 edges (self-attention)
2) Inter-image edges : 서로 다른 이미지의 keypoints 간의 edges (cross-attention)

Equation 3
$^{(l+1)}x_i^A$ $=$ $^{(l)}x_i^A$ $+$ $MLP([^{(l)}x_i^A \space || \space m_{\varepsilon \to i}])$

• 위의 식처럼 self- and cross-attention을 통해 얻은 aggreagation인 $m$와 keypoint Encoder을 MLP 연산을 통해서 update를 해준다.
• 그리고, ResNet처럼 residual하게 이전 정보를 더해준다.
• 학습 과정 중, $l$ 값에 따라 $\epsilon$를 self-attention을 할 지, cross-attention을 할 지 정한다.

  As such, starting from $l = 1, \epsilon = \epsilon_{self}$ if $l$ is odd and $\epsilon = \epsilon_{cross}$ if $l$ is even.

Attentional Aggregation

이제부터 위에서 나온, $m$이 어떻게 만들어지는지 과정을 알려준다.

Equation 4
$m_{\varepsilon \to i} \space = \displaystyle\sum_{j:(i,j) \in \varepsilon} \alpha_{ij}v_j$

$\alpha_{ij} = Softmax_j(q_i^T, k_j)$

Equation 5
$q_i = W_1^{(l)}\space x_i^Q + b_1$

${k_j}\brack{v_j}$ $=$ ${W_2}\brack{W_3}$$^{(l)}x_j^S$ $+$ ${b_2}\brack{b_3}$

• $m$은 위 수식과 같이 만들어 지는데, 그럼 $q, k, v$가 무엇인가.
  이는 attention mechanism에서 나오는 개념이다. 각각 $q$(query), $k$(key), $v$(value)이다. 문자 그대로 $q$는 원하는 대상을 찾기 위한 질문이고, key는 value를 대표한 내용, value는 실제 값이다.
• 예를 들어, query로 '6.25와 관련된 책을 찾고 싶어'의 내용을 가지면, '6.25', '임진왜란', '대공황'과 같은 key 중에서 '6.25'의 값과 행렬곱 연산에서 높은 값이 나올 것이고, softmax 함수를 통해 0~1 사이의 높은 확률로 표현될 것이다.
• 이를 value에 실제로 반영하여, 실제 정보를 특정 확률(비율)로 업데이트 해서 학습을 하고, 관련 정보를 남기는 것이다.
  (이 부분 이해하는 것이 제일 힘들었다...)
• 추가적으로 여기서 $q$, $k$, $v$는 (Equation 5)와 같이 정의되고, 이때, $W$와 $b$값들은 학습 가능한 파라미터들이다.
• 최종적으로 (Equationt 3)을 마지막 과정까지 반복하고 없는 keypoints encoder을 아래 식과 같이 linear projections 해서 final matching descriptors를 얻는다.

Equation 6
$f_i^A$ $= W \cdot$$^{(L)}x_i^A$ $+ \space b, \space\space\space\space\space\space\space\space$ $\forall i \in A,$

• 이 $f$는 $A$와 $B$ 각각을 통해 구해진다.
• 결국 $f$가 의미하는 것은 $i$ 번째 keypoint와 가장 matching 가능성이 높은 (똑같다고 판단하는) $j$의 정보가 담긴 행렬이다.

3-2. Optimal matching layer

• 이제 matching feature을 구했으니 $P$를 구할 차례다.
• 대부분의 graph matching formulation에서는 $P$는 score matrix $S \in \R^{M \times N}$와 (Equation 1 전제 하에) $\sum_{i,j}S_{i,j}P_{i,j}$ 값이 최대가 되도록 함으로써 구한다.

Score Prediction

• 모든 매칭을 별도로 표현하는 것은 비용이 많이 든다.

  Equation 7
  $S_{i,j} = <f_i^A, f_j^B>,$ $\space\space\space \forall (i, j) \in A \times B,$ $\space \space < \cdot >$is the inner product.

• 그래서 위의 식처럼 내적을 통한 유사도로 Score matrix $S$를 만든다.

Occlusion and Visibility

• unmatched keypoints들을 위해서 dustbin 행과 열을 $N+1$과 $M+1$ index에 추가하고 $z$(a single learnable parameter)로 채운다.

  Equation 8
  $\overline{S}_{i,N+1} = \overline{S}_{M+1,j} = \overline{S}_{M+1, N+1} = z \in \R.$

• 두 이미지가 똑같은 상황의 이미지가 아니다보니 반드시 match가 되지 않는 keypoints 역시 존재한다. 만약 dustbin row와 column이 없다면, 엉뚱한 match가 이뤄지고 이는 올바른 match에 대한 노이즈로 작용할 수 있다. (왜냐하면 최대 1쌍의 match만 존재한다고 전제했기 때문이다.)

Sinkhorn Algorithm

Equation 9
$\overline{P}1_{N+1} = a \space\space\space\space and \space\space\space\space$ $\overline{P}^T1_{M+1} = b.$
$a = [1_M^T \space\space\space\space N]^T,\space\space$ $b = [1_N^T \space\space\space\space M]^T$

• (Equation 9)를 통해서 얻은 이산 확률 분포 $a, b$와 비용행렬로 볼 수 있는 $\overline {S}$를 통해서 differentiable optimal transport problem으로 볼 수 있고, 이는 Sinkhorn Algorithm을 통해서 해결이 가능하다.
• 여기서 Sinkhorn 알고리즘은 각 행과 열에 softmax 함수를 적용한 것과 비슷한 효과를 준다.
• T iterations을 거친 후, $\overline P$에서 dustbins을 제거하여 P를 얻는다.
  (Q 의문 : 왜 다시 P로 바꾸는지... 어짜피 P^-에서 loss를 계산할건데... 어짜피 최종 단계라서 더 P를 쓸 일도 없는데....)

3-3. Loss

Equation 10
$Loss = - \displaystyle\sum_{(i,j) \in M} \log{\overline{P}_{i,j}}$ $- \displaystyle\sum_{i \in I} \log{\overline{P}_{i,N+1}}$ $- \displaystyle\sum_{j \in J} \log{\overline{P}_{M+1,j}}$
$M = \{(i,j)\} \subset A \times B.$

1) Ground truth matches인 $M$ 집합을 기반으로 올바른 $(i, j)$ 조합에 해당하는 index 부분의 $P$ matrix의 값의 negative 로그합

2) dustbin row의 label(정답)인 $I$ 집합을 기반으로 올바른 $i$에 해당하는 index 부분의 $P$ matrix의 값을 negative 로그합 (= unmatch 되어야 하는 애들을 dustbin에 제대로 모아서 오답인 $(i, j)$ 조합을 만들지 않게 기여하므로 precision과 recall 값을 높이는 효과를 준다.

3) dustbin column의 label(정답)인 $J$ 집합을 기반으로 올바른 $j$에 해당하는 index 부분의 $P$ matrix의 값을 negative 로그합 (= unmatch 되어야 하는 애들을 dustbin에 제대로 모아서 오답인 $(i, j)$ 조합을 만들지 않게 기여하므로 precision과 recall 값을 높이는 효과를 준다.

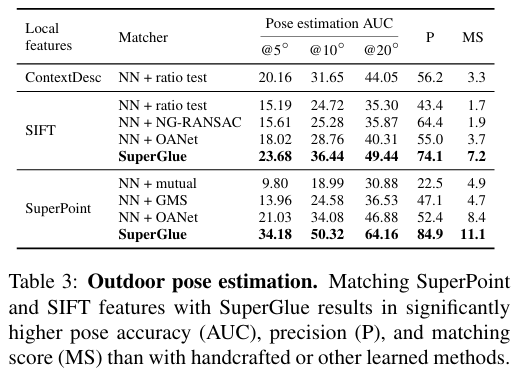
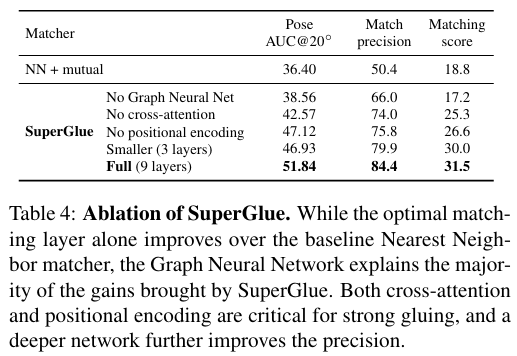
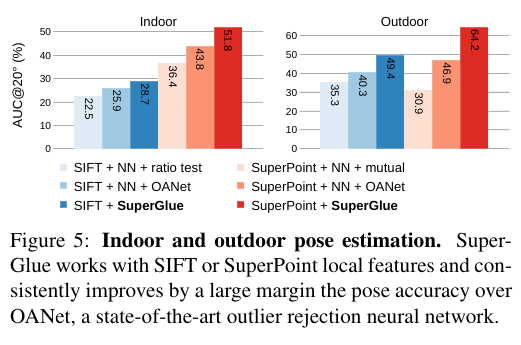
4. 주요 결과 :

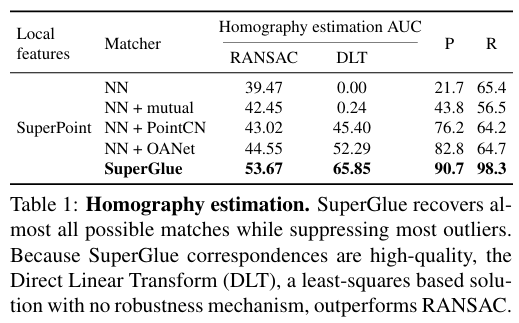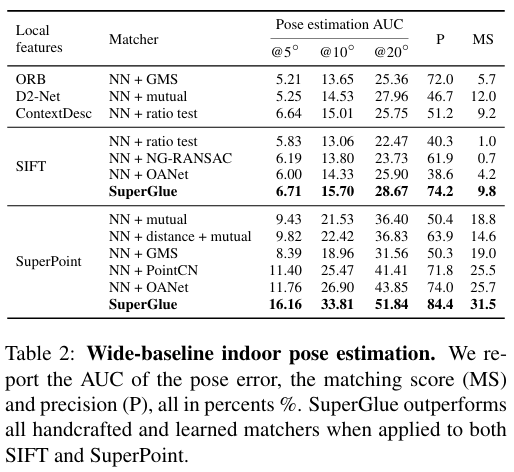5. Comment

: CV와 NLP가 전혀 다른 영역이라 생각했는데, attention 메커니즘을 이렇게도 쓸 수 있다는게 새로웠습니다. 유명하고 좋은 생각의 재료는 관심 분야가 아니더라도 공부할 필요성을 느꼈습니다.

더 자세한 내용은 논문 원본을 참고하시기 바랍니다.

개인의 주관이 반영된 해석이라 논문의 의도와 다를 수 있습니다. 
오류가 있다면 댓글로 알려주시면 감사하겠습니다!