[논문 리뷰] GNNExplainer: Generating Explanations for Graph Neural Networks

논문 링크 : GNNExplainer: Generating Explanations for Graph Neural Networks

1. 선택하게 된 이유

: GNN에 대한 폭넓은 지식 습득을 위해 시도입니다.

2. 서론

• 다음 3가지 이유 때문에, GNN prediction을 이해하는 것은 유용한다.

  1. GNN model에 대한 신뢰를 높일 수 있다.
  2. 증가하는 많은 decision-critical applications에 대한 model의 투명성을 높일 수 있다.
  3. practitioners이 network 특징들에 대해 이해할 수 있고, 모델로 인한 문제에 대한 systematic patterns을 식별하고 고칠 수 있다.

• GNN의 graph structure 과 feature information은 complex models와 설명하기 힘든 예측을 야기한다.

• 다른 종류의 neural networks를 설명하는 최근 접근들은 two main routes 중 하나를 택해왔다.

  1. 간단한 모델로 근사한다.
  2. relevant features을 위해 모델을 조사하고 high level features에 대한 좋은 질적 해석을 찾거나 영향력 있는 input instances를 식별한다.

• 하지만, 이 접근들은 그래프의 핵심인 relational information을 incorporate하는 능력을 떨어뜨린다.

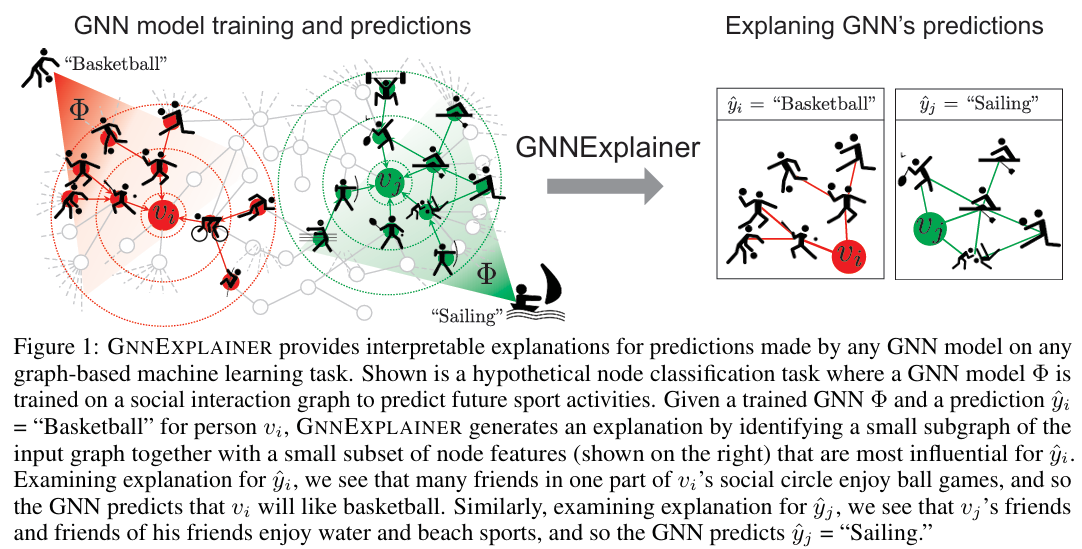
• GNNExplainer은 GNN의 예측에 중요한 역할을 한 compact subgraph structure과 small subset of node features를 식별한다.
• GNNExplainer은 model에 상관없이 GNN의 예측에 대한 해석가능한 설명을 제공한다.
• 또한, entire class of instances의 consistent하고 concise한 설명을 만들어낸다.
• 마지막으로, interpretability와 의미적으로 관련된 구조를 시각화할 수 있다.

• GNNExplainer GNN이 학습되는 전체의 그래프의 rich subgraph의 설명을 specifiy 한다. 그 subgraph는 GNN의 예측과 함께 mutual information을 최대화한다.
• 이는 mean field variational approximation을 계산하거나 GNN의 computation graph의 중요한 subgraph를 선택하는 real-valued graph masks을 학습하거나 안중요한 node features을 제외하는 feature mask을 학습해서 통해 달성될 수 있다.

• 그래프가 아닌 neural networks에 대한 interpretability methods를 two main families로 그룹화했다.

  1. full neural networks에 대한 간단한 proxy model을 계산한다.
  2. 계산에서 중요한 측면을 식별한다.

• 하지만, 이 방법들도 몇몇 경우에서는 잘못된 결과를 만들어내고, gradient sturation같은 결과를 야기한다.
• 해석하지 않는 방법을 새로 안만드는 것은 그래프같은 relational structures을 활용하지 않았다.
• attention mechanisms으로 해석하는 것은 학습된 edge attention values가 모든 노드에 대한 예측에 대해 모두 같은 값이었다. 이는 다른 노드의 label이 아닌 특정 노드의 label을 예측해야할 때 중요한 edge인 many applications에 모순된다.

3. 방법론(a): Formulating explanations for graph neural networks

기호 설명
Let $G$, graph on edges $E$ and nodes $V$
$X = \{x_1,...,x_n\}, x_i \space \in \space \R^d$, $d$-dimensional node features $X$

Let $f$, label function on nodes, $f : V \mapsto \{1,...,C\}$, maps every node in $V$ to one of $C$ classes

3-1. Background on graph neural networks

• layer $l$에서 GNN model $\Phi$에 의한 update는 3가지 계산을 가진다.

  • $m^l_{ij} = MSG(h_i^{l-1},h_j^{l-1},r_{ij})$
    $m^l_{ij}$ is the message for node pair ($v_i$,$v_j$), $r_{ij}$ is the relation between the nodes.
    
    
  • $M^l_i = AGG(\{m^l_{ij} | v_j \space \in \space N_{v_i}\})$, where $N_{v_i}$ is neighborhood of node $v_i$
    $M^l_i$ is an aggregated message by GNN.
    
    
  • $h^l_i = UPDATE(M^l_i,h_i^{l-1})$
    $h^l_i$ is $v_i$'s representations in $l$ layer.
    
    
  • $z_i = h_i^L$
    $z_i$ is the final embedding for node $v_i$ after L layers of computation.

• 그렇게 마지막 계산을 통해 임베딩 $z$을 얻는다.

3-2. GNNExplainer: problem formulation

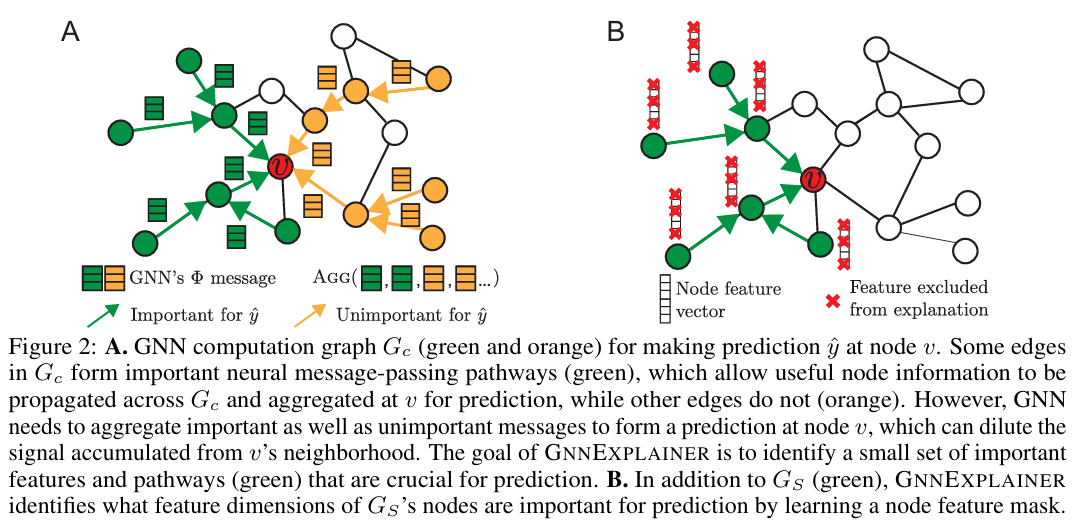
(Figure 2A)

• computation graph of node $v$을 $G_c(v)$, $A_c(v) \space \in \space \{0,1\}^{n \times n}$, $X_c(v) = \{x_j | v_j \space \in \space G_c(v)\}$이라 할 때, GNN model $\Phi$는 conditional distribution $P_{\Phi}(Y | G_c,X_c)$를 학습한다.
• $Y$는 random variable representing labels {1,...,C}, 즉, 1~C 중 하나라는 말.
• $P_{\Phi}(Y | G_c,X_c)$는 nodes이 C classes 중 각각에 속할 확률.
• $G_c(v)$는 그래프 구조 정보를, $X_c(v)$는 노드 특징 정보를 가지고 있다.

(Figure 2B)

• GNNExplainer는 예측 $y$에 대한 설명을 ($G_S$, $X^F_S$)으로 생성한다.
• $G_S(v)$는 small subgraph of the computation graph이고, $X_S$는 feature of $G_S$, $X^F_S$는 small subset of node features (노드 특징 중 마스크로 거른 뒤 정보)

4. 방법론(b): GNNExplainer

4-1. Single-instance explanations

• $MI$(mutual information) 사용해서 중요성을 형식화하고 GNNExplainer을 다음의 최적화 framwork을 활용해서 formulate한다.

  Equation 1
  $\displaystyle{\max_{G_s}}MI(Y,(G_S,X_S)) = H(Y) - H(Y | G = G_S, X = X_S)$

• $MI$는 $v$의 computation graph와 node features를 $G_S$와 $X_S$로 제한될 때, $\hat y = \Phi(G_c, X_c)$의 확률 변화를 수치화하다.
• 예를 들면, 특정 node나 edge를 지워보고 $\hat y$에 대한 확률이 많이 감소하면, 중요한 지표에 대한 반증으로 판단한다.
• (Equation 1)에서 entropy term $H(Y)$는 상수이기 때문에(왜냐하면, 파이는 trained GNN이기 때문에 fixed이기 때문에), $H(Y|G=G_s, X=X_s)$를 최소화하는 문제로 바뀐다.

Equation 2
$H(Y | G = G_S, X = X_S) = -\mathbb{E}_{Y|G_S,X_S}[\log P_{\Phi}(Y|G=G_S,X = X_S)]$

• $H(Y|G=G_s, X=X_s)$는 위와 같은 식으로 표현될 수 있다.
• 따라서, prediction $\hat y$에 대한 설명은 GNN 계산이 $G_S$로 제한될 때, $\Phi$의 불확실성을 최소화하는 subgraph $G_S$이다.
• 실제로 (Figure 2)에서 $G_S$가 $\hat y$확률을 극대화한다.
• 간결한 설명을 위해서, $G_S$의 size를 제한하도록 강요한다. ($|G_s| \le K_M$)
• 실제로, 이는 GNNExplainer가 $G_c$의 denoise에 초점이 맞춰져 있다는 것을 암시한다.

GNNExplainer's optimization framework.

• $G_S$가 너무 많아서 GNNExplainer를 직접 최적화하는 것은 쉽지 않다.

• 따라서, subgraph $G_S$에 대한 fractional adjacency matrix (즉, $A_S < [0, 1]^{n \times n}$, hard하게 0, 1로 이루어진게 아니라 0~1 사이로 이루어진 soft한 방법)를 고안한다. 그리고 subgraph의 제약을 모든 $j, k$ 에 대해 $A_S[j, k] \le A_c[j, k]$로 강제하다.

• 이런 연속 완화(soft한 방식)은 $G_c$의 subgraphs의 분포를 근사하는 방법이다. (즉, 우회해서 최적화를 구하는 방법이다.)

• 특히 랜덤 그래프 변수($G_s \text{\textasciitilde} \varsigma$)를 사용해서 (Equation 2)는 아래와 같은 (Equation 3)이 된다.

  Equation 3
  $\displaystyle\min_{\varsigma} \mathbb{E}_{G_s \text{\textasciitilde} \varsigma} H(Y|G=G_S,X=X_S)$

• 그리고, 볼록하다고 가정했을 때, 젠슨 부등식을 통해서 (Equation 3)의 upper bound(쉽게 최대값이라고 생각)인 (Equation 4)를 구할 수 있다.

  Equation 4
  $\displaystyle\min_{\varsigma} H(Y|G=\mathbb{E}_{\varsigma}[G_S],X=X_S)$

• neural networks의 복잡성 때문에 종종 (볼록하다는) 가정이 맞지 않지만, 실험적으로 위 식이 종종 고품질 설명에 해다하는 local minimum에 도달하는 것을 확인했다.

• 기대값 $\mathbb{E}_{\varsigma}$를 효율적으로 추정하기 위해 mean-field variational approximation(쉽게, 가장 흔한 것에 근사하는 방법.)를 사용하거나 $\varsigma$를 multivariate 베르누이 분포(여러 개의 이진 변수를 가진 데이터 분포를 각각의 이진 변수에 대한 베르누이 분포로 나누어 표현. $P(x_1,x_2,...,x_n) = P(x_1)P(x_2)...P(x_n)$로 분해한다.

  $P_{\varsigma}(G_S) = \Pi_{(j,k) \in G_c} A_S[j,k]$

• 이를 통해, A_s를 구할 수 있다. 그리고 mean-field approximation을 통해 볼록하지 않아도 local minimum에 도달하는 것을 관찰했다.

• (Equation 4)의 conditional entropys는 $\mathbb{E}_{\varsigma}[G_S]$를 $A_c \odot \sigma(M)$ ($M$는 우리가 학습해야할 mask, $\odot$는 element-wise multiplication, $\sigma$는 sigmoid 함수)로 바꾸므로써 최적화될 수 있다.

• 다음 두 가지의 질문에 답하기 위해, conditional entropy에서 cross entropy로 바꿨다.

  1. "why does the trained model predict a certain class label" (trained model이 특정 클래스 레이블을 예측하는 이유)
  2. "how to make the trained model predict a desired class label" (trained model이 원하는 클래스 레이블을 예측하도록 만드는 방법)

Equation 5
$\displaystyle{\min_M} - \displaystyle\sum^C_{c=1} \mathbb{1} [y=c] \log P_{\Phi}(Y=y | G=A_c \odot \sigma(M), X=X_c)$

• 계산적으로 효율적인 최종 버전인 수식이다.

4-2. Joint learning of graph structural and node feature information

Equation 6
$X^F_S = \{x_j^F | v_j \space \in \space G_S\}$, $x_j^F = [x_{j,{t_1}},...,x_{j,{t_k}}]$ for $F_{t_i} = 1$

• 예측값 $\hat y$에 대해 가장 중요한 node features이 무엇인지 식별하기 위해 GNNExplainer은 $G_S$에서 노드의 feature selector $F$를 학습한다.
• 모든 노드의 특징들로 이루어진 $X_s$를 사용하기 보다, GNNExplainer를 $G_S$의 노드의 특징들의 부분집합인 $X^F_S$를 고려한다.
• 이를 (Equation 1) 과정에 적용한다.

  Equation 7
  $\displaystyle{\max_{G_s}}MI(Y,(G_S,F)) = H(Y) - H(Y | G = G_S, X = X_S^F)$

Learning binary feature selector $F$.

• $\hat y$에 대한 예측 확률이 떨어지지 않는 특징들은 중요하지 않다고 가정하여, $F$를 통해 걸러낸다.
• 하지만, 가끔 예측에 중요한 특징이 걸러지는 문제가 발생해서 다음의 방법으로 이를 해결했다.

  1. marginalize over all feature subsets
  2. use Monte caro estimate
  3. use reparametrization trick
     
     
     $X = Z + (X_S - Z) \odot F$ s.t. $\sum_j F_j \le K_F$
     $Z$ is a $d$-dimensional random variable sampled from the empirical distribution
     $K_F$ is a parameter representing the maximum number of features to be kept in the explanation.

4-3. Multi-instance explanations through graph prototypes

• GNNExplainer는 다음 2가지 stages를 통해서 multi-instance explanations을 제공한다.

  1. 특정 class $c$에 해당하는 $v$ 노드들에 대한 각각의 single-instance explanations을 align한다.
  2. robust median-based approach를 사용하여 align된 adjacency matrices에서 graph prototype A_proto를 얻는다. Prototype A_proto는 같은 class($c$)의 노드들의 그래프 패턴에 대한 insights를 제공한다. 그리고, prototype과 특정 노드의 예측에 대한 single-instace explanations를 비교하며 학습한다.

4-4. GNNExplainer model extensions

• GNNExplainer는 다음의 특징을 가진다.

  1. Any machine learning task on graphs - ENNExplainer는 최적화 알고리즘을 수정하지 않고, node classification, link prediction, graph classification를 설명할 수 있다.
  2. Any GNN model - input graph로 GNN 기반의 message passing architectures를 사용했기 때문에, 어떤 GNN model에도 적용할 수 있다.
  3. Computational complexity - GNNExplainer의 최적화는 computation model $G_c$에 영향을 많이 받는데, computation graphs는 전형적으로 비교적 작다.

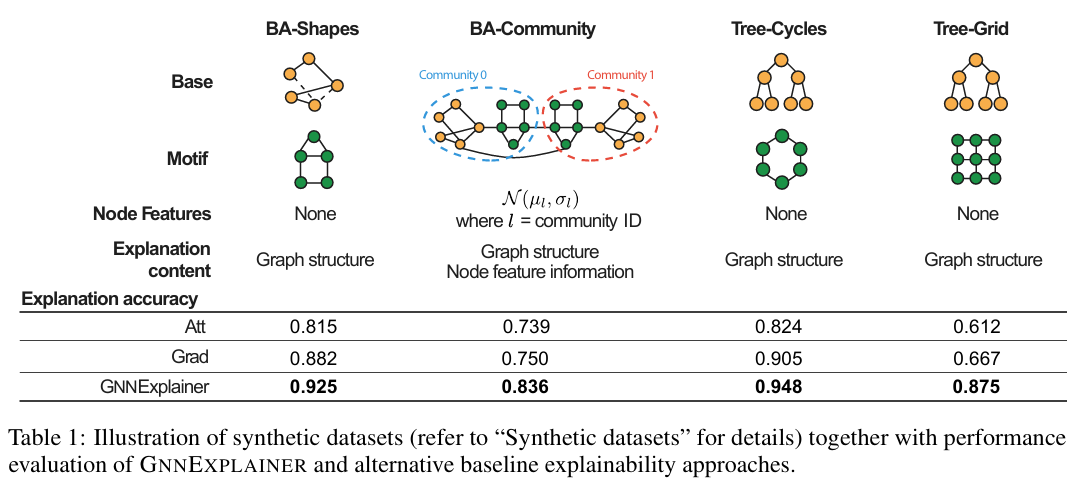
5. 주요 결과

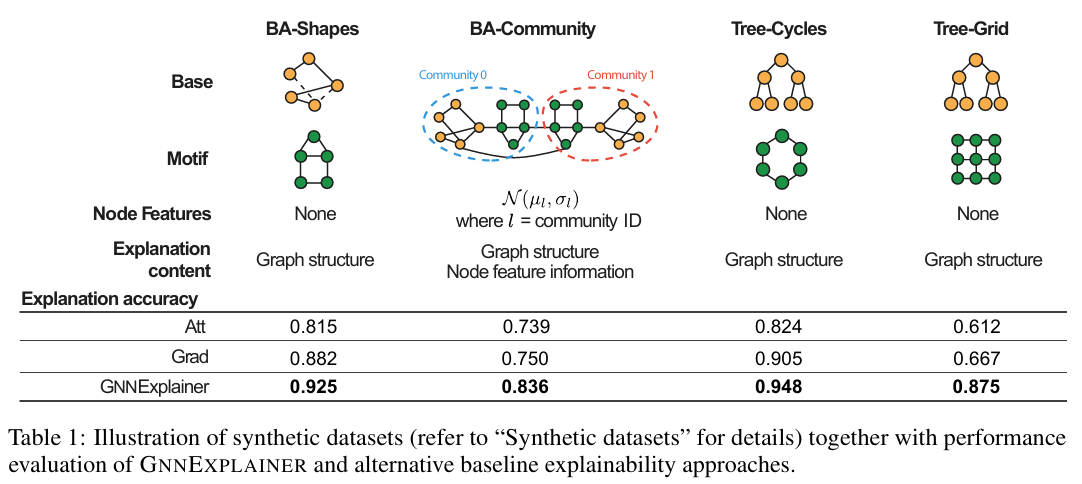
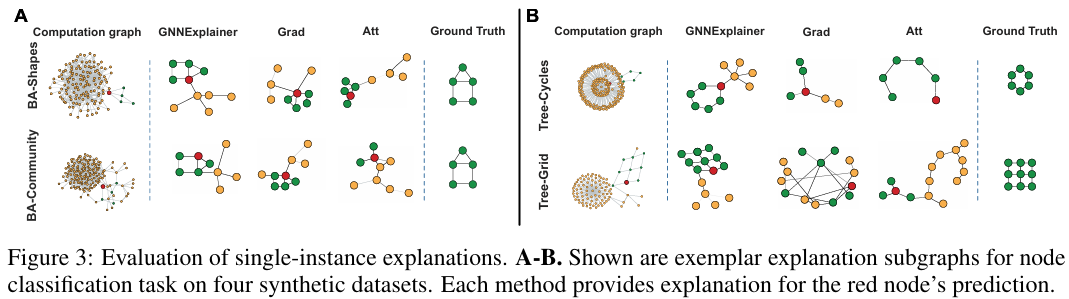
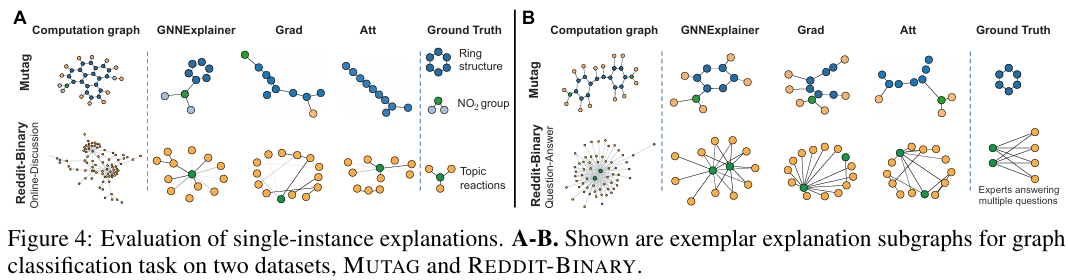
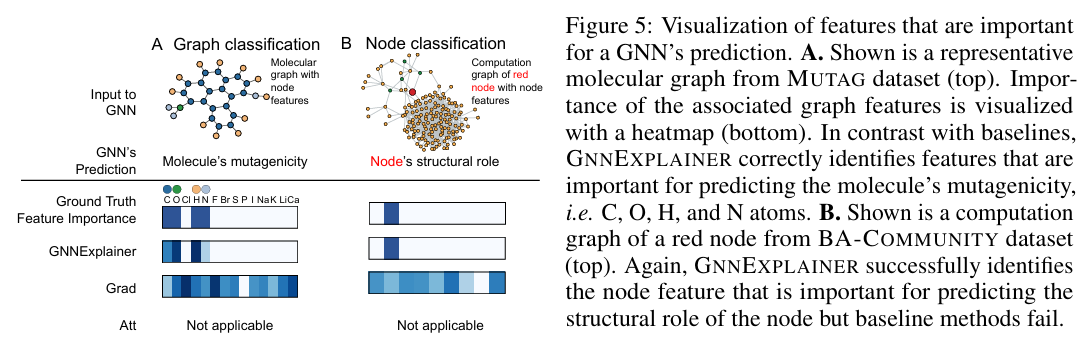
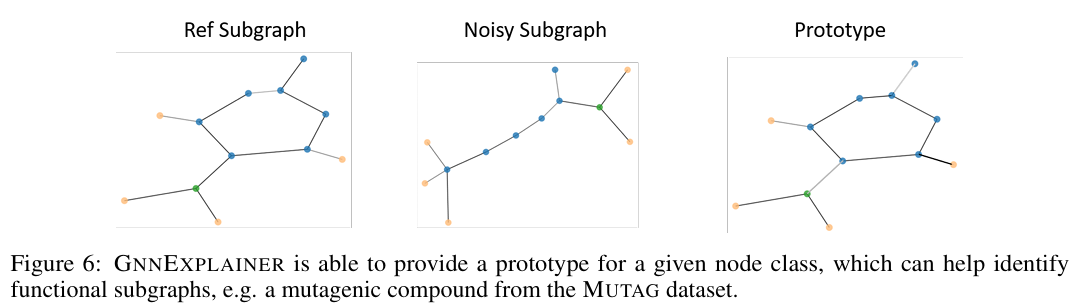
6. Comment
: XAI에 대해서 처음 접해보는 경험이었고, 다양한 확률과 통계적인 공식들과 익숙하지 않은 최적화 방법에 이해하는데 시간과 노력이 많이 들어갔다. 또한, 직관적이지 않아서 이해가 쉽지 않아서 어려웠다.

더 자세한 내용은 논문 원본을 참고하시기 바랍니다.

개인의 주관이 반영된 해석이라 논문의 의도와 다를 수 있습니다. 
오류가 있다면 댓글로 알려주시면 감사하겠습니다!