[논문 리뷰] Link Prediction Based on Graph Neural Networks

논문링크 : Link Prediction Based on Graph Neural Networks

1. 선택하게 된 이유

: GNN을 공부하다보니 Link Prediction에 대한 내용이 많이 나오고 그에 따른 유명한 논문을 찾아보다 보게 됐습니다.

2. 서론

• 각각의 target link 주변의 local subgraph를 추출하므로써 subgraph의 패턴을 link existence에 맵핑하는 함수를 학습할 수 있다.
• 그러므로, 자동적으로 현재 network에 맞는 휴리스틱을 학습한다.

• Link Prediction은 network의 두 노드들이 link를 가질 수 있는지 아닌지를 예측하는 것이다.
• 휴리스틱 방법들은 links에 대한 가능성을 나타내는 몇몇의 heuristic node similarity scores를 계산한다.
• 하지만, 모든 휴리스틱은 두 노드들이 link되어 있을 것이라는 중요한 가정이 필요하다.
• 그래서 주어진 network에서 적절한 휴리스틱을 학습하는 것이 합리적인 방법이다.

• 사실은 heuristics는 graph structure features에 속한다. 왜 속하는지 아직 이해하지 못했다.
• heuristics는 predefined graph structure feature로 볼 수 있기 때문에, 위에서 휴리스틱이 자동적으로 학습했던 것처럼. network에서 graph structure feature을 학습할 수 있다고 볼 수 있다.
• 이 논문 이전의 link prediction performance에서 state-of-the-art은 WLNM이다.
• WLNM은 어떤 enclosing subgraphs이 link existence에 해당하는지를 학습하는 FCN(full-connected neural network)를 사용한다.
• 그리고,학습데이터로 사용할 links 주변의 local enclosing subgraphs를 추출한다.
• enclosing subgraph는 $h$에 따라 $x, y$의 이웃의 집단에 의해 유도된 subgraph이다.
  앞으로는 heuristics를 graph structure feature로 해석해야 자연스러울 것입니다.

• high-order 휴리스틱일수록 효과적이지만, 시간과 메모리를 감당하기 힘들다.
• 하지만, $\gamma$-decaying 이론을 통해서 단일화되어서 낮은 $h$ 값으로도 high-order feature를 학습할 수 있다.

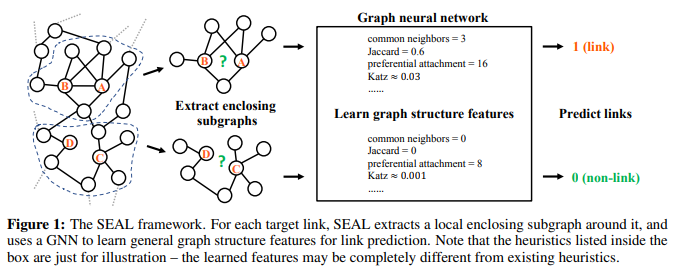
• SEAL은 local enclosing subgraphs의 그래프 구조를 학습한다. 여기서 local한 enclosing subgraphs를 학습 데이터로 사용할 수 있는 이유는 $\gamma$-decaying이론으로 정당화된다.
• 그리고, SEAL은 위에서 설명한 WLNM 기법에서 크게 2가지를 변형해서 만들었다.

  1. FCN(full-connected neural network)을 GNN으로 대체했다.
  2. Subgraph 구조 뿐 아니라 노드 feature도 학습한다.

Preliminaries
1. Notations
Let $G = (V,E)$ be an undirected graph, where $V$ is the set of vertices and $E \subseteq V \space \times \space V$ is the set of observed links
adjacency matrix $A$, where $A_{i,j} = 1$ if $(i,j) \in E$ and $A_{i,j} = 0$ otherwise
any nodes $x,y \in V$, let $\varGamma(x)$ be the 1-hop neighbors of $x$
$d(x,y)$ be the shortest path distance between $x$ and $y$.
walk $w = <v_0,\cdot\cdot\cdot,v_k>$ is a sequence of nodes with $(v_i,v_{i+1}) \in E$.
$|<v_0,\cdot\cdot\cdot,v_k>|$ is the length of the walk $w$, which is $k$ here.


2. Latent features and explicit features

1) Latent features methods는 각가의 노드에 대한 낮은 차원의 latent representation/embedding을 학습하기 위해 network의 matrix representations를 인수분해(factorize)한다.

2) Explicit features은 각 노드들에 대한 모든 형태의 side information를 node atrributes의 형태로 이용할 수 있다.

3. Graph neural networks
GNN은 크게 2가지 종류의 층으로 이루어져 있다.

1) graph convolution layers : 각각의 노드들에 대해 local substructure features를 추출한다.

2) graph aggregation layer : node-level features을 graph-evel feature vector로 종합한다.

많은 graph convolution layers은 message passing framework로 단일화된다.

4. Supervised heuristic learning
supervised heuristics를 학습하려했던 시도들은 3가지 한계점을 가지고 있었다.

1) FCN(full-connected network)는 오직 fixed-size tensors만 input으로 허용하기 때문에, WLNM은 다양한 subgraphs을 같은 크기로 truncating 해야한다.

2) adjacency matrix representations의 한계 때문에, WLNM은 latent or explicit features를 학습할 수 없었다.

3) 이론적 정당화(like $\gamma$-decaying 이론)가 존재하지 않았다.

3. 방법론 (a) : A theory for unifying link prediction heuristics

• 이제는 다양한 link prediction heuristics의 뒤의 메커니즘을 깊게 이해해볼 것이다.
• 그렇게, local subgraphs로부터 휴리스틱을 학습하는 방법을 영감받을 것이다. 여기서 local이라는 점은 굉장히 중요하다.

Definition 1 (Enclosing subgraph)

• graph $G = (V,E)$, given two nodes $x, y \in V$
• the $h$-hop enclosing subgraph for $(x,y)$ is the subgraph $G^h_{x,y}$
• $G^h_{x,y}$의 노드들은 $\{i | d(i,x) \leq h$ or $d(i,y) \leq h \}$를 만족한다.

Theorem 1 Any $h$-order heuristic for $(x,y)$ can be accurately calculated from $G^h_{x,y}$

• 왜냐하면, $G^h_{x,y}$가 $h$-order heuristic for $(x,y)$를 모두 포함하기 때문이다.
• 앞으로의 분석을 통해 high-order heuristics을 낮은 $h$로 실행할 수 있다.
• 그리고, certain conditions에서 $\gamma$-decaying 휴리스틱은 h-hop enclosing subgraph에서 잘 근사될 수 있다.
• 또한, 잘 알려진 휴리스틱도 $\gamma$-decaying 휴리스틱 framwork에 의해 단일화될 수 있다.

Definition 2 ($\gamma$-decaying heuristic)
Equation 1
$H(x,y) = \eta \displaystyle{\sum^{\infin}_{l=1} \gamma^l f(x,y,l)}$

• $\gamma$은 0~1사이의 값을 가지는 decaying factor
• $\eta$은 positive constant 혹은 최대값이 상수로 제한되는 $\gamma$의 positive function
• $f$는 $x,y,l$의 nonnegative function

Theorem 2 Given a $\gamma$-decaying heuristic $H(x,y) = \eta \sum^{\infin}_{l=1} \gamma^l f(x,y,l)$, if $f(x,y,l)$ satisfies

• (property 1) $f(x,y,l) \leq \lambda^l$ where \lambda < \1/\r
• (property 2) $f(x,y,l)$ is calculable from $G^h_{x,y}$ for $l = 1,2,\dotsb,g(h)$, where $g(h) = ah + b$ with $a,b \in \N$ and $a > 0$
• 이를 만족할 경우, $H(x,y)$는 $G^h_{x,y}$로부터 근사될 수 있다.

Proof $\gamma$-decaying heuristic을 그것의 첫 $g(h)$까지 합으로 근사할 수 있다.
Equation 2
$\tilde{H} (x,y) := \eta \displaystyle\sum^{g(h)}_{l=1} \gamma^l f(x,y,l)$

• 근사 오류의 상한선은
• $|H(x,y) - \tilde{H}(x,y) |= \eta \displaystyle{\sum^{\infin}_{l= g(h)+1} \gamma^l f(x,y,l)} \leq \eta \displaystyle{\sum^{\infin}_{l=ah+b+1}} \gamma^l \lambda^l = \eta (\gamma\lambda)^{ah+b+1} (1-\gamma\lambda)^{-1}$
• 작은 $\gamma\lambda$와 큰 $a$일수록 decreasing speed가 더 빠르다.

Lemma 1 Any walk between $x$ and $y$ with length $l \leq 2h + 1$ is include in $G^h_{x,y}$
proof $d(v_i, x) \ge h+1$ and $d(v_i,y) \ge h+1$라 가정했을 때, $2h+1 \ge l = |<x,v_1,\dotsb,v_i>| + |<v_i,\dotsb,v_{l-1},y>| \ge d(v_i, x) + d(v_i, y) \ge 2h+2$이므로 모순

• 따라서 $d(v_i,x)$와 $d(v_i,y)$는 모두 $h$보다 작거나 같다. 따라서 모든 $v_i$는 $G^h_{x,y}$에 포함되어 있다.
• 앞으로 3가지의 유명한 high-order 휴리스틱을 분석할 것이다.

3-1. Katz index

Equation 3

• $walks^{<l>}(x,y)$은 $x$부터 $y$까지의 길이 $l$의 walk의 집합이다.
• $A^l$은 adjacency matrix의 $l$번 거듭제곱한 것이다.
• $x,y$ 사이의 길이가 $l$인 모든 walks의 모음을 통한 Katz index 합은 $\beta^l$ (0 < $\beta$ < 1)를 통해서 짧은 walks에 더 가중치를 부여해서 완하된다.

• Katz index는 $\gamma-decaying$에서 $\eta = 1$, $\gamma = \beta$, $f(x,y,l) = |walks^{<l>}(x,y)|$를 사용한 것이다.
• Lemma1를 통해서 $|walks^{<l>}(x,y)| = l$이고, '$l \leq 2h + 1$'을 만족하기 때문에, $g(h) \leq 2h + 1$인 a,b를 잘 고르면 (property 2)를 만족한다.
  이 부분 이해하는게 힘들었다. 변수들이 생겨나고 결정되는 선후관계를 잘 고려해보길 바란다.
  

Proposition 1. 모든 $i,j$에 대해서 $[A^l]_{i,j}$의 상한선이 $d^l$이다. 여기서 $d$는 최대 인접한 노드의 개수(degree)이다.
proof

• 수학적 귀납법으로 증명하자면, $l =1$일때, 모든 $(i,j)$에 대해서 $A_{i,j} \leq d$만족한다.
• $l$일 때 가능하다고 모든 $(i,j)$ $[A^l]_{i,j} \leq d^l$라고 가정했을 때,
  $[A^{l+1}]_{i,j} = \displaystyle{\sum^{|V|}_{k=1} [A^l]_{i,k}A_{k,j} \leq d^l \displaystyle{\sum^{|V|}_{k=1}}A_{k,j} \leq d^ld = d^{l+1}}$

i부터 j까지 l+1 길이로 도착하는 edge가 존재하는지에 대한 배열이 A이다. 위 식을 통해서는 l까지 j의 직전 노드(k)까지의 edge 정보에 k부터 j까지의 edge 정보를 반영해서 최종 edge에 대한 배열을 0과 1로 표현하는 배열

이 부분을 이해하는게 상당히 힘들었다.

나는 d는 i부터 j까지 l+1의 길이로 갈 수 있는 최대 경우의 수(모두 갈 수 있다고 가정했을 때의 최대 인접한 노드의 개수)로 이해했다.

• 이를 통해, $l+1$일 때도 가능하다는 것을 알 수 있으므로 참이다.

• $\lambda = d$일 때, $d < {1 \over \beta}$만 만족하면 (property 1)를 만족한다. 근데, $\beta$는 5E-4와 같은 작은 수 이기 때문에, Katz는 $h$-hop enclosing subgraph로부터 잘 근사할 수 있다.

3-2. PageRank

• 노드 $x$에 대한 PageRank는 $x$부터 random walker의 정적 분포(stationary distribution)를 계산한다.
  정적분포 : 마르코프 체인(현재상태가 미래상태에 영향을 미치는 확률 모델)에서 쓰이는 개념. 정적분포를 만족하는 벡터 $\pi$는 $\pi P=\pi$를 만족한다. 여기서는 P는 전이 확률 분포를 의미한다.
• 쉽게 말해, 현재 위치부터 $\alpha$의 확률로 랜덤으로 이웃으로 움직이거나, $1-\alpha$의 확률로 $x$로 return하는 것을 말한다.
• $\pi_x$는 stationary distribution vector(정적 분포 벡터)이고, $[\pi_x]_i$는 node $i$로 random walker할 확률이다.

  Equation 4
  $\pi_x = \alpha P \pi_x + (1 - \alpha) e_x$

• $P$는 전이 행렬이고, 만약 $(i,j) \in E$이면, $P_{i,j} = {1 \over {|\varGamma(v_j)|}}$이고, 그렇지 않다면, $P_{i,j} = 0$이다.
• $e_x$는 $x^{th}$의 원소는 1을 가지고, 아닌 것은 0을 가지는 벡터다.
• the inverse P-distance theory를 통해서 PageRank의 기반이 $\gamma$-decaying 휴리스틱임을 보일 것이다.

  Equation 5
  $[\pi_x]_y = (1 - \alpha) \displaystyle\sum_{w:x\leadsto y} P[w]\alpha^{len(w)}$

• $w = <v_0,v_1,\dotsb, v_k>$, $len(w) := |<v_0,v_1,\dotsb,v_k>|$
• $P[w]$는 $\prod^{k-1}_{i=0} {1 \over |\varGamma(v_i)|}$ 이다. 즉, w를 지나면서 해당 edge를 타고갈 확률의 곱

  Equation 6
  $[\pi_x]_y = (1 - \alpha) \displaystyle\sum^{\infin}_{\substack{{w:x\leadsto y}\\len(w)=l}} P[w]\alpha^{len(w)}$

• $f(x,y,l) := \sum_{\substack{{w:x\leadsto y}\\len(w)=l}}P[w]$라고 할 때, $f(x,y,l)$은 $x$로부터 모든 노드로 갈 확률들의 합이므로 최대 1을 넘을 수 없고, 이는 $f(x,y,l) \leq 1 < {1 \over \alpha}$를 만족한다.($\because$ $0 \leq \alpha \leq 1$)
• 따라서, (property 1) 만족한다.
• Lemma 1에 의해 (property 2)도 만족한다.

3-3. SimRank

• SimRank score는 만약 두 노드 각각의 이웃들이 비슷하다면 두 노드는 비슷할 것이다라는 직관에서 시작한다.

  Equation 7
  $s(x,y) := \gamma{\sum_{a\in {\varGamma(x)}} \sum_{b\in {\varGamma(y)}} s(a,b) \over |\Gamma(x)| \cdot |\Gamma(y)|}$

• $\gamma$는 0~1 사이의 값을 가진다.
  코사인 유사도 수식과 유사하다.

  Equation 8
  $s(x,y) = \displaystyle{\sum_{w:(x,y) \multimap (z,z)}} P[w] \gamma^{len(w)}$

• $w : (x,y) \multimap (z,z)$는 all simultaneous walks를 의미한다. 하나의 walk은 x에서 시작하고, 다른 walk은 y에서 시작한다.
• 그리고, 처음 만나느 어떤 vertex가 $z$이다.
• $P[w]$는 $\prod^{k-1}_{i=0} {1 \over |\varGamma(v_i)\varGamma(u_i)|}$이다. 각각의 노드의 edge 개수 중 하나씩을 고를 확률
• 확률이니까 $f(x,y,l) \leq 1 < {1 \over \gamma}$이어서 (property 1)을 만족한다.
• 서로 이웃 탐방하다가 만나는 거니까 양쪽 시작하여 기존 방식들과 달리 절반이 되어 $l \leq h$이다.
• 따라서, (property 2)도 만족한다.

Discussion

• $\gamma$-decaying 휴리스틱으로 적은 근사오류로 근사가 가능하고 이는 획기적이다. 이를 통해 local enclosing subgrpah는 충분한 정보를 가지고 있음을 알 수 있다.

4. 방법론 (b) : SEAL : An implemetation of the theory using GNN

• SEAL은 $\gamma$-decaying 휴리스틱과 같은 특별한 형태의 features를 학습하는 것이 아니라, general graph structure feature를 학습한다.
• 이는 3가지 단계를 포함하고 있다.

  1. sampled positive links (observed)와 sampled negative links (unobserved)를 위한 enclosing subgraph extraction
  2. node information matrix construction
  3. GNN learning

• GNN은 전형적으로 $(A,X)$를 input으로 가지고, $A$(with slight abuse of notation) 는 adjacency matrix이고, $X$는 node information matrix이다.
• node information matrix은 3가지 components를 가진다. 1) structural node labels, 2) node embeddings, 3) node attributes

4-1. Node labeling

• node labeling function $f_l : V \to \N$ 은 enclosing subgraph의 모든 노드 i를 integer label $f_l(i)$에 할당한다.
• labeling을 하는 목적은 노드들의 다른 역할에 다른 labels를 사용하기 위해서이다.
• 만약, labeling을 하지 않는다면, 어디가 target인지 GNN이 알 수 없다.
• 그래서 다음과 같이 크게 두가지로 labeling을 진행한다.

  1. The two target nodes $x$ 와 $y$는 항상 distinctive label "1"를 가진다.
  2. 만약 $d(i,x) = d(j,x)$이고 $d(i,y) = d(j,y)$이면, node $i$ 와 $j$에는 같은 label를 부여한다.

     1) 만약 $d(i,x) + d(i,y) \ne d(j,x) + d(j,y)$이면, $d(i,x) + d(i,y) < d(j,x) + d(j,y) \lrArr f_l(i) < f_l(j)$
     2) 만약 $d(i,x) + d(i,y) = d(j,x) + d(j,y)$이면, $d(i,x)d(i,y) < d(j,x)d(j,y) \lrArr f_l(i) < f_l(j)$. (이는 기하학적으로 distance를 비교한 것이다.)

• 이런 labeling을 통해서 노드들의 상대적인 position과 structural importance도 반영한다.
• $d(i,x) = \infin$ or $d(i,y) = \infin$이면 null label 0을 부여한다. 이렇게 하는 것이 안하는 것보다 성능이 좋았다.
• labeling 후에는 one-hot 인코딩을 진행하여, $X$를 만든다.

Appendix B. More discussion about node labeling

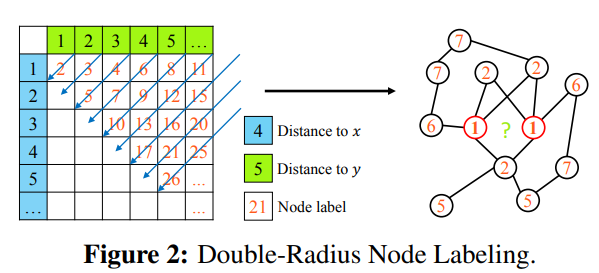
• enclosing subgraphs는 본질적으로 방향성을 가지고 있다.
• node labeling 알고리즘은 DRNL 알고리즘을 적용한다.
• node labeling은 structual information을 더해준다.
• 또한, 노드들의 상대적 위치들과 center로부터 그들의 distance를 반영한다.
• 하지만, 크기 infromation은 one-hot encoding 이후 사라지기 때문에, node labels의 one-hot encoding에서는 이용할 수 없다.
• 그래도, 그런 labeling은 node labels이 training으로 directly하게 사용될 때나 node를 rank를 매길 때, potentially useful하다.
• $d(i,x)$를 계산할 때, 일시적으로 $y$를 지운다. ($\because$ $y$를 타고 distance가 달라질 수 있기 때문이다.)
• SEAL의 node labels은 WLNM에 비해서 별로 정밀하지 않아도 된다.

4-2. Incorporating latent and explicit features

• node information matrix $X$는 latent and explicit features를 포함하고 있다.
• network $G = (V, E)$에서 sampled positive training links $E_p \subset E$라고 하고 sampled negative training links $E_n \cap E = \text{\O}$이라고 하자.
• 근데, 그렇게 설정을 하고 $G$를 노드 임베딩하면, $E_p$의 정보를 가지고 있어서, GNN이 link existence information을 빨리 찾아내고 거기에 최적화를 해버린다.
• 이는 $E_p$에 치우쳐진 일반화가 되기 때문에, 문제가 된다.
• 그래서 $G' = (V, E \cup E_n)$으로 노드 임베딩을 진행한다.

Appendix E. Configuration details of SEAL

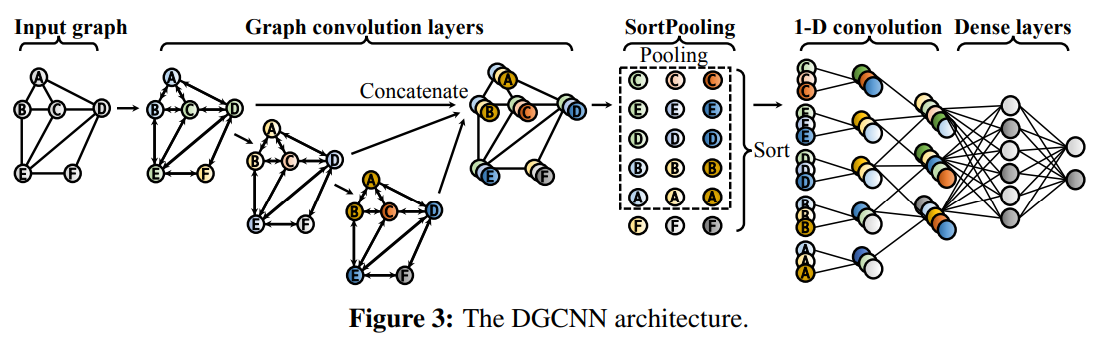
• 이 논문에서는 GNN으로 DGCNN을 사용했다.
• DGCNN은 propagation(전파) 기반의 graph convolution layers과 새로운 graph aggragation(집계) layer인 SortPooling으로 이루어져 있다.

  • $Z = f(\tilde{D}^{-1} A~ XW)$
  • $A~ = A + I$
    해당 노드 자신에 대해서는 edge가 없으니 추가해주기. 자기 자신으로 향할 수 있다는 확률을 추가해주는 듯. 혹은, edge가 없는 노드일 수 있음을 방지하는 조치인 것 같다.
  • $D~_{i,i} = \sum_j A~_{i,j}$
    각 노드에 연결된 edge를 모두 총합해서 대각행렬에 위치시킨다.
  • $W \in \R^{c \times c}$는 학습가능한 graph convolution parameters
  • $f$는 비선형 활성화 함수이다.
  • 위 식을 해석하자면, $W$를 곱하므로써 linear transformation을 적용하고, propagation matrix $D^{-1}A$를 통해서, 이웃 노드들에게 전파한다.
    $D^{-1}$은 구해지는 과정을 보면, 0~1의 값을 가지게 되고, 이를 조금더 깊게 이해하면, 특정 edge 중 그 edge로 갈 확률을 내포하고 있다고 해석할 수 있다.
  • $Z_i = f({1 \over{|\Gamma(i)|} +1} [X_iW + \displaystyle{\sum_{i \in \Gamma(i)} X_jW]}$
    해당 노드의 특징과 주변 노드의 특징들에 가중치를 부여하고 평균을 내서 살릴 특징을 정하고, 비선형 활성화 함수$f$를 통과하여 노드 i에 대한 새로운 노드 상태로 update를 한다.

• 위 식은 node information과 노드 $i$의 이웃으로부터 first-order structure pattern를 요약한다.
• GNN 층을 거친 후, 그저 더해버리면 노드 각가의 정보가 상당히 없어질 수 있기 때문에, max-$k$ Pooling 을 사용한다.
• max-$k$ Pooling은 sorted representations의 sizes를 unify한다.
  DGCNN은 4개의 층으로 이루어져 있다.

  1) 32,32,32,1 channels
  2) SortPooling layer
  3) two 1-D convolution layers (16 and 32 output channels)
  4) dense layer (128 neurons)

• graph classification model에 input으로 넣기 전에, 두 target nodes 사이의 edge를 제거한다. 왜냐하면, edge가 link existence information를 포함할 수 있기 때문이다.

5. 주요 결과

• SEAL는 link prediction 부분에서 뛰어나고 robust한 framework임을 결과를 통해 알 수 있다.

• 그리고 Appendix E에서 알 수 있듯이, SEAL은 어떤 GNN이나 node embedding 기술을 사용해도 된다는 장점이 있다.
  

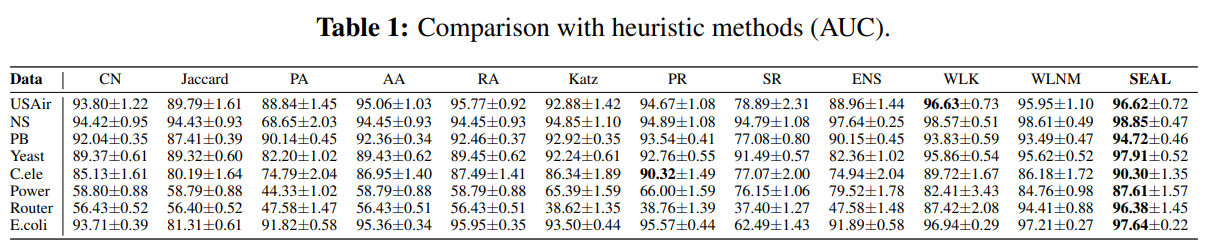
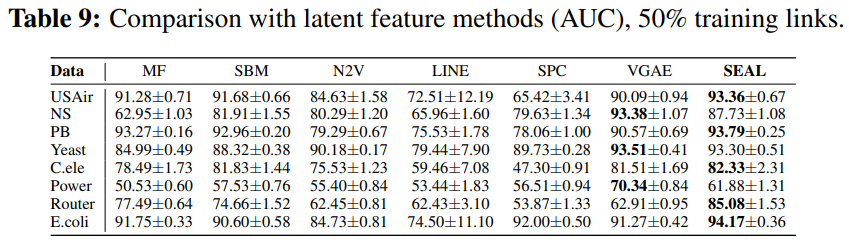
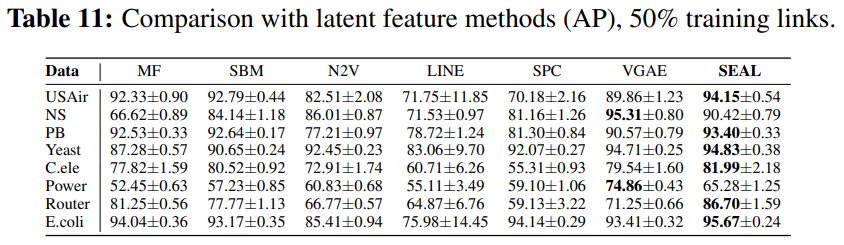
• (Table 1)을 통해서 learned 'heuristics'가 더 잘 notwork properties를 찾아내는 것을 알 수 있다.
  

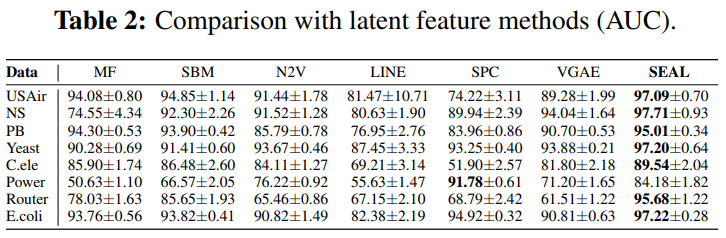
• (Table 2)를 통해서 large margin의 순수한 node2vec 임베딩보다 SEAL과 함께한 node2vec 임베딩의 성능이 더 좋았다.

• (Table 1)과 (Table 2)를 비교해보면, (Table 2)가 더 높은 부분도 있음을 통해, joint learning이 항상 성능은 높이는 것은 아니라는 것을 알 수 있다.
  
  
  
  
  
  
  
  
  
  

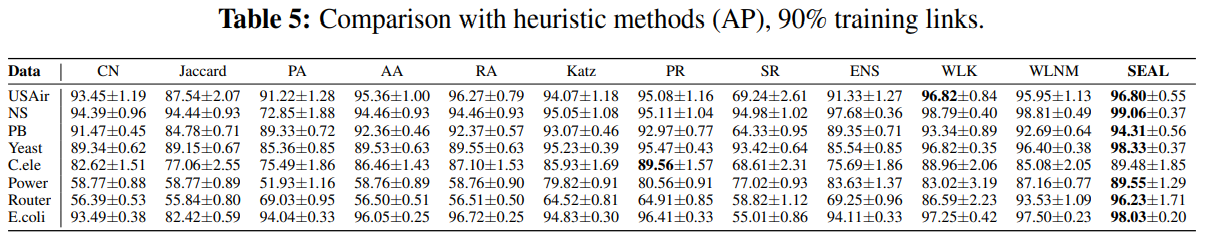
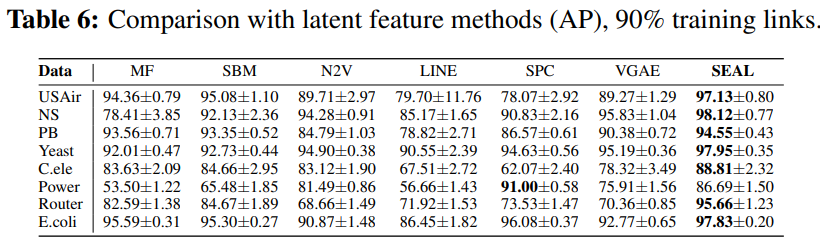
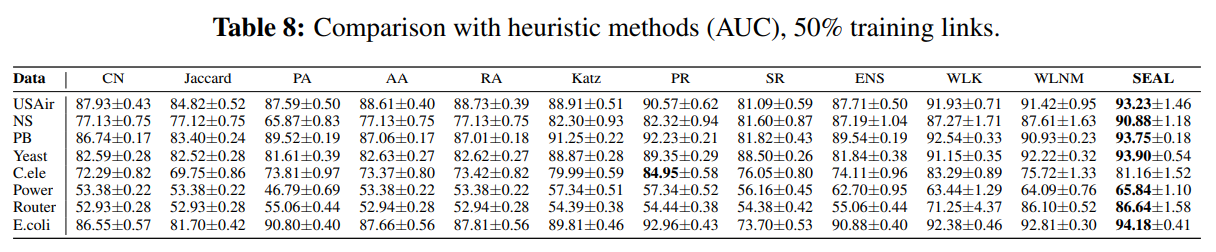
6. Comment
: GNN 관련 논문을 읽을수록 자주 등장하는 adjacency matrix과 같은 표현들이 눈에 익으니, 이해하는 속도가 붙고 더 깊게 이해할 수 있는 것 같아서 기분이 좋았습니다. GNN의 input으로 subgraph를 넣는 것이 당연하고만 생각했지 왜? entire graph가 아니라 subgraph를 사용하지?라는 의문을 가지지 못한 자신을 반성할 수 있게 되었습니다.

더 자세한 내용은 논문 원본을 참고하시기 바랍니다.

개인의 주관이 반영된 해석이라 논문의 의도와 다를 수 있습니다. 
오류가 있다면 댓글로 알려주시면 감사하겠습니다!