[논문 리뷰] Denoising Diffusion Probabilistic Models

논문링크 : Denoising Diffusion Probabilistic Models

1. 선택하게 된 이유

: Diffusion 모델의 성능이 상당히 좋다는 점에서 감명받았고, transformer와 같은 중요한 논문이라고 판단해서 리뷰하게 됐습니다.

2. 서론

• 이 논문에서 소개할 diffusion probabilistic model은 nonequilibrium thermodynamics(비평형 열역학)의 개념들에 영감을 받았다.
• Langevin dynamics(동역학)을 사용한 노이즈 제거 점수 매칭과 diffusion probabilistic model 간의 새로운 연결(관계)에 따라 설계된 weighted variational bound(가중 변분 경계)를 사용하여 학습하므로써 최고의 결과를 얻었다.

variational bound(변분 경계)는 variational Inference(변분 추론)에 사용되는 도구로, 주어진 데이터에 대한 log likelihood의 하한을 제공한다.
$\log p(X) \geq \mathbb{E}_{q(z)}[\log p(X,z)] - D_{KL}(q(z) || p(z|X))$
와 같은 형태를 가진다.

variational inference(변분 추론)은 복잡한 확률 분포를 근사하기 위해 사용되는 방법이다. 특히, 베이지안 모델(조건부 확률)에서 사후 확률 분포를 계산하는데 유용하다.

변분 추론은 1. 모델 정의(데이터와 모델을 정의하고, 사전 분포(prior)와 우도(likelihood)를 설정한다.) 2. 사후 분포 근사(복잡한 사후 확률 분포를 간단한 분포(예, 가우시안)로 근사한다. 이 근사 분포를 (q)라고 한다.) 3. 최적화(실제 사후 분포와 근사 분포 간의 차이를 최소화하는 방향으로 (q)를 최적화한다. 이때, 변분 경계를 활용해서 최적화 문제를 해결한다.)

• 이 모델은 progressive lossy decompression scheme(점진적인 손실 압축 해제 방식 : 일부 정보를 손실하면서 점차 원래 데이터로 복원하는 방식)을 사용하며, 이는 autoregressive decoding(자기 회귀 디코딩)의 일반화 버전이라고 볼 수 있다.
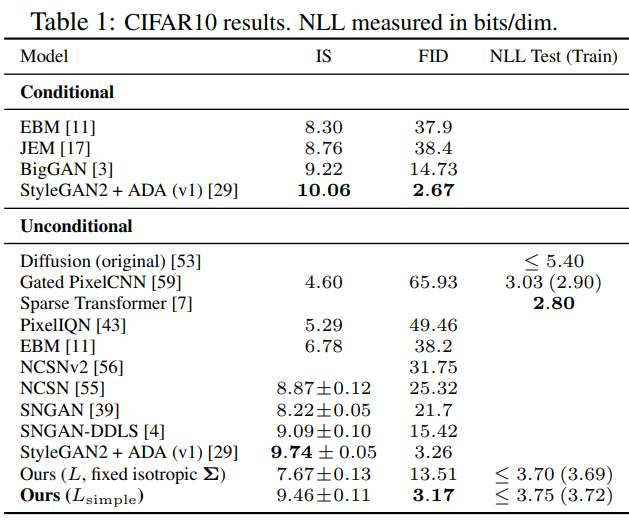
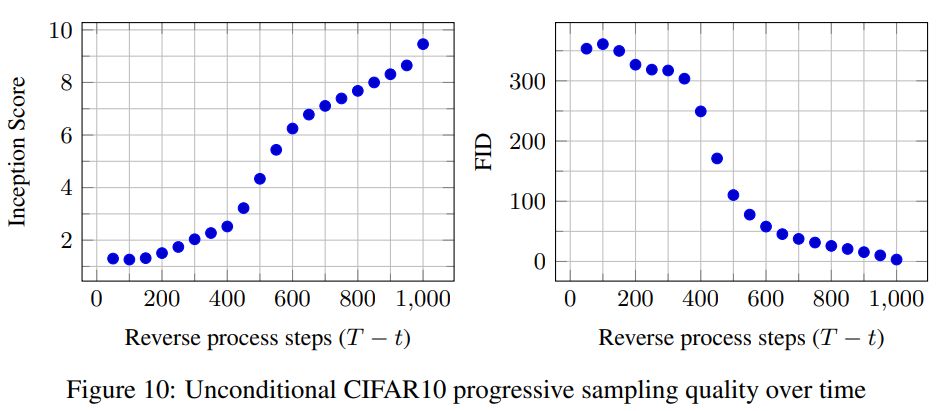
• unconditional CIFAR10 dataset에서는, 9.46의 Inception score를, 3.17의 FID score를 얻었다.

Inception score는 이미지 품질 & 다양성 측정에 사용되는 지표다. 
생성된 이미지가 다양한 클래스에 걸쳐 균형 잡힌 분포를 가질수록 높은 점수

FID score는 생성 이미지와 실제 이미지의 차이를 측정하는 지표다. 
특징 벡터 분포를 비교해서 구하고 낮을수록 두 이미지가 유사함을 의미한다.

• $256\times256$ LSUN에서는, ProgressiveGAN과 비슷한 sample(생성된 이미지) quality를 보였다.

• 다양한 종류의 Deep generative models은 최근에 높은 quality samples를 보여준다.
• energy 기반 modeling과 score matching에서 GANs의 이미지들과 비교될만한 이미지를 만들어내는 두드러진 발전이 있다.
• diffusion probabilistic model(앞으로 diffusion model)은 데이터(예, 원본 사진)와 맞는 samples(예, 생성 사진)을 생성하는 variational inference를 사용해서 학습된, 파라미터화된 Markov chain(마르코프 체인)이다.
• 마르코프 체인의 transitions은 diffusion process(signal이 없어질 때까지 sampling과정의 반대 방향으로 점진적으로 노이즈를 더하는 마르코프 체인)의 반대로 학습된다
• transitions 과정이 소량의 가우시안 노이즈로 이루어지면, smpling chain transition을 조건부 가우시안(마르코프 체인)으로만 설정해도 충분하고, 이를 통해 간단한 신경망 파라미터화가 가능하다.

• diffusion model은 정의하기 간단하고, 학습하기 효율적이지만, 어떻게 diffusion model이 높은 quality samples을 만들어낼 수 있는지에 대한 증명은 없다.
• 그래서 아래 2가지를 선 보일 것이다.

  1. diffusion models이 정말로 높은 quality samples를 만들어 낼 수 있는지
  2. diffusion models의 특정한 parameterization이 학습 중에는 multiple noise level에 대한 denoising score matching과 같은지, sampling 중에는 annealed Langevin dynamics 기법과 같은지

• 높은 sample quality에도 불구하고, 우리 모델들은 ,다른 모델들과 달리, 경쟁력 있는 log likelihoods가 없다. (하지만, energy 기반 모델과 score matching 모델을 위한 샘플링 기법(annealed importance sampling)을 사용한 large estimates보다는 좋은 log liklihoods를 가졌다.)
• 우리 모델의 손실 없는 codelengths(비트 수)의 대부분은 감지할 수 없는 이미지 디테일을 설명하는데 쓰인다.
• diffusion model의 샘플링 과정은 autoregressive decoding과 같은 progressive decoding 중 하나라는 것을 보일 것이다.

3. 방법론(a) : Background

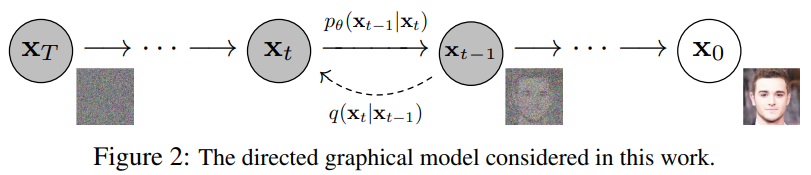
• diffusion models은 $p_{\theta}(x_0) := \int p_{\theta}(x_{0:T}) dx_{1:T}$ 형태의 latent variable models이다.
• 여기서, $x_1,\dotsb,x_T$는 데이터 $x_0 \sim q(x_0)$와 동일한 차원을 가진 잠재 변수다.
• joint distribution(결합 분포) $p_{\theta}(x_{0:T})$은 reverse process이라고 하고, $p(x_T) = N(x_T;0,I)$에서 시작하는 학습된 가우시안 transitions를 가진 Markov chain(마르코프 체인)으로 정의된다.
  $p(x_T) = N(x_T;0,I)$은$x_T$에서의 상태를 나타내고 이는 표준 가우시안 분포와 같은 형태를 띤다고 이해했다

  Equation 1
  $p_{\theta}(x_{0:T} := p(x_T) \displaystyle\prod^T_{t=1}p_{\theta}(x_{t-1}|x_t)$
  $p_{\theta}(x_{t-1}|x_t) \coloneqq N(x_{t-1}; \mu _{\theta}(x_t,t),\Sigma_{\theta}(x_t,t))$
  $\Sigma$는 공분산 기호이다.
여기서 평균을 중심으로 공분산의 정도만큼 데이터가 확률적으로 변화하게 된다고 이해했다.
그리고$x_T$에서 출발해서 거기에 확률 곱 연산을 통해서 가우시안 분포에 따르는 확률적 변화를 적용하는 것이라고 이해했다.

• diffusion models이 다른 종류의 latent variable models과 구분되는 점은 forward process or diffusion process로 부르는 approximate posterior(근사 후방 확률 분포) $q(x_{1:T} | x_0)$에 있다.
• 이 $q(x_{1:T} | x_0)$는 variance schedule(분산 스케줄) $\beta_1,\dotsb,\beta_T$에 따라 점진적으로 가우시안 노이즈를 데이터에 더하는 Markov chain이다.

  Equation 2
  $q(x_{1:T} | x_0) \coloneqq \displaystyle\prod^T_{t=1} q(x_t | x_{t-1})$
  $q(x_t | x_{t-1}) \coloneqq N(x_t; \sqrt{1 - \beta_t}x_{t-1}, \beta_t I)$
  $x_0$에서$x_T$로 가우시안 분포에 따른 노이즈를 계속 적용한다
위의 reverse process는 학습을 통해서 diffusion process의 각 단계별 확률적 변화를 맞춘다면(알아낸다면) 원래 이미지로 복원할 수 있다는 점을 이용할 것 같다.
아직 왜 variance schedule을 통해서$x_{t-1}$와 $I$가 아닌$\sqrt{1 - \beta_t}x_{t-1}, \beta_t I$로 스케일링 했는지는 잘 이해하지 못했다.

• 학습은 일반적인 variational bound(변분 바운드)를 최적화하여 negative log likelihood를 최소화한다.

  Equation 3
  $L \coloneqq \mathbb{E}[-\log p_{\theta}(x_0)] \leq \mathbb{E}_q [- \log {{p_{\theta}(x_{0:T})} \over {q(x_1:T | x_0)}}] = \mathbb{E}_q [- \log p(x_T) - \displaystyle\sum_{t \geq 1} \log {{p_{\theta}(x_{t-1} | x_t)} \over {q(x_t | x_{t-1})}}]$

• forward process의 variances $\beta_t$는 reparameterization을 통해서 학습될 수 있고, hyperparameters로 상수로 설정할 수 있다.
• reverse process의 expressiveness은 $p_{\theta}(x_{t-1} | x_t)$에서 가우시안 조건부의 선택에 의해 부분적으로 보장된다.
• 왜냐하면, 두 과정(forward and reverse process)은 $\beta_t$가 작을 때, 같은 functional form(기능적인 구조)를 가졌기 때문이다.
• forward process의 두드러지는 장점은 $\alpha_t \coloneqq 1 - \beta_t$ and $\bar{\alpha}_t \coloneqq \prod^t_{s=1} \alpha_s$를 사용해서 임의의 timestep $t$에서 $x_t$를 닫힌 형태로 샘플링할 수 있다는 것이다.
  쉽게 말해서, 매번 마르코프 체인을 통해서 반복적인 계산을 하지 않아도, (Equation 4)를 통해서 $x_T$에 해당하는 샘플링을 한번에 구할 수 있다는 것이다.

  Equation 4
  $q(x_t | x_0) = N(x_t; \sqrt{\bar{\alpha}_t} x_0, (1-\bar{\alpha}_t) \Iota)$

• stochastic gradient descent(확률적 경사 하강법)을 사용해서 random terms of $L$를 최적화하므로써 효율적인 학습이 가능하다.

• (Equation 3)를 식변형을 통해서 (Equation 5)로 만들면, 성능을 높일 수 있다.

  Equation 5
  $\mathbb{E}_q [\underbrace{D_{KL}(q(x_T | x_0) || p(x_T))}_{L_T} + \displaystyle\sum_{t>1} \underbrace{D_{KL}(q(x_{t-1} | x_t, x_0) || p_{\theta}(x_{t-1} | x_t))}_{L_{t-1}} \underbrace{- \log p_{\theta}(x_0 | x_1)}_{L_0}]$

• (Equation 5)는 $p_{\theta}(x_{t-1} | x_t)$와 $x_0$를 조건에 두었을 때, 쉽게 계산 가능한 forward process posteriors를 비교하는 KL divergence(쿨백-라이블러 발산)을 사용한다.
  (쿨백-라이블러 발산)은 두 확률 분포 간 차이를 측정하는 비대칭적인 거리 척도를 나타낸다. 즉, 두 분포가 상대적으로 얼마나 다른지를 나타낸다.

  Equation 6
  $q(x_{t-1} | x_t, x_0) = N(x_{t-1}; \tilde{\mu}_t(x_t, x_0), \tilde{\beta}_t \Iota)$
  
  
  Equation 7
  $\tilde{\mu}_t(x_t, x_0) \coloneqq {{\sqrt{\bar{\alpha}_{t-1}} \beta_t} \over {1 - \bar{\alpha}_t}} x_0 + {\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1} \over {1 - \bar{\alpha}_t}} x_t$
  $\tilde{\beta}_t \coloneqq {{1 - \bar{\alpha}_{t-1}} \over {1 - \bar{\alpha}_t}} \beta_t$

• 결론적으로 (Equation 5)의 모든 KL divergences는 가우시안 분포끼리의 비교이다.

4. 방법론(b) : Diffusion models and denoising autoencoders

• diffusion model은 다음 3가지를 골라야 한다.

  1. forward process에서 variances $\beta_t$
  2. model architecture
  3. reverse process에서 가우시안 분포 parameterization

• 3-2.에서는 diffusion models과 denoising score matching 사이의 새로운 관계를 만들었다.

4-1. Forward process and $L_T$

• 이 논문에서는 forward process variances $\beta_t$를 reparameterization에 의해 학습가능한 변수가 아닌 상수 값으로 고정했다.
• 그러므로, approximate posterior $q$는 학습 가능한 parameters(변수)가 없고, $L_T$는 상수 값을 가진다. (그래서 딱히 고려하지 않아도 된다.)

4-2. Reverse process and $L_{1:T-1}$

• $p_{\theta}(x_{t-1} | x_t) = N(x_{t-1}; \mu_{\theta}(x_t,t), \Sigma_{\theta}(x_t, t))$ for $1< t \leq T$에 대해서 살펴보자.
• 우선, $\Sigma_{\theta}(x_t, t) = \sigma^2_t \Iota$ 학습되지 않는 시간 의존 상수로 설정한다.
• 실험적으로, $\sigma^2_t = \beta_t$와 $\sigma^2_t = \tilde{\beta}_t = {{1 - \bar{\alpha}_{t-1}} \over {1- \bar{\alpha}_t}} \beta_t$로 각각 설정했을 때, 결과가 비슷했다.
• 다음 2가지 선택에 의해 reverse process entropy의 상향선과 하향선과 같다.

  1. $x_0 \sim N(0,\Iota)$에 대해 optimal
  2. 한 점으로 결정되는 $x_0$에 대해 optimal

• 평균 $\mu_{\theta}(x_t, t)$를 represent하기 위해서 specific parameterization을 제안한다.
• $p_{\theta}(x_{t-1} | x_t) = N(x_{t-1}; \mu_{\theta}(x_t, t), \sigma^2_t \Iota)$라는 점을 통해서

  Equation 8
  $L_{t-1} = \mathbb{E}_q[{1 \over {2 \sigma^2_t}} || \tilde{\mu}_t (x_t, x_0) - \mu_{\theta}(x_t, t) ||^2] + C$
  $C$는 $\theta$에 영향받지 않는 상수다.
  Equation 8에서 쓰인 형식은$D_{KL}$에서 분산은 비슷하니 평균차이만 고려하는 것 같다.
그리고, 실제 평균에서 추측한 평균을 빼서 제곱하고 2x(분산)으로 나누는 것은 통계적 가설 검증 or 신뢰 구간 설정 시 주로 사용한다고 한다.

• 그러므로, $\mu_{\theta}$에 대한 간단한 parameterization은 forward process posterior의 평균인 $\tilde{\mu}_t$를 예측하는 모델이다.
• 하지만, $x_t(x_0, \epsilon) = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon$로 (Equation 4)를 reparameterizing하고, (Eqauation 7)를 적용해서 (Equation 8)를 확장하여 (Equation 10)를 만들 수 있다.
• 여기서 $\epsilon \sim N(0, \Iota)$
  Equation 8에서 Equation 9로 넘어갈 때, 위의 Equation 4 reparameterizing이 쓰인다. reparameterizing은 정규분포의 의미(평균$\sqrt{\bar{\alpha}_t} x_0$에서 시작하여 분산$\sqrt{1 - \bar{\alpha}_t} \epsilon$에 의한 불확실적 변화)만 가져와서 수식으로 풀어쓴 것이다.

  Equation 9
  $L_{t-1} - C = \mathbb{E}_{x_0, \epsilon} \big[{1 \over {2 \sigma^2_t}} || \tilde{\mu}_t \big( x_t(x_0, \epsilon), {1 \over{\sqrt{\bar{\alpha}_t}}} (x_t(x_0, \epsilon) - \sqrt{1 - \bar{\alpha}_t \epsilon}) \big) - \mu_{\theta}(x_t(x_0, \epsilon), t)||^2 \big]$
  
  
  Equation 10
  $L_{t-1} - C = \mathbb{E}_{x_0, \epsilon} \big[{1 \over {2 \sigma^2_t}} || {1 \over {\sqrt{\alpha_t}}} \big( x_t(x_0, \epsilon) - {{\beta_t} \over {\sqrt{1 - \bar{\alpha}_t \epsilon}}} \big) - \mu_{\theta}(x_t(x_0, \epsilon), t)||^2 \big]$
  Equation 9에서 Equation 10으로 넘어갈 때, Equation 7의 관계식을 적용한 것이다.

• (Equation 10)는 $\mu_{\theta}$가 $x_t$가 주어질 때, 반드시 ${1 \over {\sqrt{\alpha_t}}}(x_t - {{\beta} \over {\sqrt{1 - \bar{\alpha}_t \epsilon}}})$를 예측한다는 것을 의미한다.

  Equation 11
  $\mu_{\theta} = \tilde{\mu}_t \big(x_t, {1 \over {\sqrt{\bar{\alpha}_t}}} (x_t - \sqrt{1 - \bar{\alpha}_t} \epsilon_{\theta}(x_t)) \big) = {1 \over {\sqrt{\bar{\alpha}_t}}} \big( x_t - {{\beta_t} \over {\sqrt{1 - \bar{\alpha}_t}}} \epsilon_{\theta}(x_t, t) \big)$
  반드시 예측한다는 점을 이용해서 등식을 만들었다.

• $x_t$는 model의 input으로 얻을 수 있으니 (Equation 11)처럼 변형할 수 있다.
• 여기서 $\epsilon_{\theta}$는 $x_t$로부터 $\epsilon$을 예측하기 위한 function approximator(학습가능한 함수 정도로 이해했다.) 이다.
• $p_{\theta}(x_{t-1} | x_t)$에서 얻어지는 $x_{t-1}$은 다음과 같이 계산할 수 있다.

  $x_{t-1} = {1 \over {\sqrt{\alpha_t}}} \big( x_t - {{\beta_t} \over {\sqrt{1 - \bar{\alpha}_t}}} \epsilon_{\theta}(x_t, t) \big) + \sigma_t z$
  $z \sim N(0, \Iota)$

• (Algorithm 2)와 데이터 밀도의 학습된 기울기(경향)인 $\epsilon_{\theta}$은 Langevin dynamics이랑 비슷하다.
  'Langevin dynamic'은 동역학에서 사용하는 개념으로 '무작위 운동 힘($\sigma_t z$, 정규분포와 같은 경향) + 결정론적 힘'을 사용하는 식이라고 이해했다.

  Equation 12
  $\mathbb{E}_{x_0, \epsilon} \big[ {{\beta^2_t} \over {2\sigma^2_t \alpha_t(1 - \bar{\alpha}_t)}} || \epsilon - \epsilon_{\theta}(\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1- \bar{\alpha}_t} \epsilon, t) ||^2\big]$

• (Equation 10)은 (Equation 11)를 통해서 (Equation 12)로 더 간단하게 표현할 수 있다.
• 이는 $t$로 index된 multiple noise scales에 대한 denoising score matching과 비슷하다.
  여기서 말하는 denoising score matching은 위에서 이야기한 FID score와 Inception socre를 말하는 것 같다.
• 그리고, (Equaiton 12)는 Langevin dynamics 역과정의 variational bound 중 하나의 항과 같다.
  Langevin dynamics 역과정은 Langevin dynamics의 과정을 예측하는 과정이다.
• 따라서, denoising score matching과 비슷한 우리의 목표를 최적화하는 것은 variational inference를 사용하는 것과 같다.

• 결론적으로, reverse process의 mean function approximator인 $\mu_{\theta}$를 학습해서, $\tilde{\mu}_t$를 예측하거나 $\epsilon$을 예측할 수 있다.

4-3. Data scaling, reverse process decoder, and $L_0$

• image data는 [-1, 1]로 선형적으로 스케일되는 {0, 1, ..., 255} 중의 정수로 이루어져 있다고 가정했다.
• 이는 reverse process가 standard normal prior인 $p(x_T)$부터 일관되게 스케일된 input에서 작동한다는 것을 보장한다.
• 이산적인 log likelihoods를 얻기 위해서, reverse process의 마지막 단계에서 독립적인 discrete(이산적) decoder를 설정했다.
• 이 decoder는 가우시안 분포 $N(x_0; \mu_{\theta}(x_1, 1), \sigma^2_1 \Iota)$에 의해 유도되고, 자세한 수식은 다음과 같다.

Equation 13
$p_{\theta}(x_0 | x_1) = \displaystyle\prod_{i=1}^D \int^{\delta_{+}(x_0^i)}_{\delta_{-}(x^i_0)} N(x; \mu_{\theta}^i(x_1, 1), \sigma^2_1) dx$
$\delta_{+}(x) = \begin{cases} \infty &\text{if } x = 1 \\ x + {1 \over 255} &\text{if } x < 1 \end{cases}$
$\delta_{-}(x) = \begin{cases} -\infty &\text{if } x = -1 \\ x - {1 \over 255} &\text{if } x > -1 \end{cases}$

• $I$는 데이터의 차원이고, $i$는 하나의 좌표 추출을 나타낸다.
• 이러한 결정은 variational bound가 이산적인 데이터에 대해서 (노이즈를 추가하거나 Jacobian 행렬을 log likelihood에 통합하는 작업 없이) lossless codelength(정보량으로 이해했다.)를 보장한다.
  Jacobian 행렬은 다변수 함수의 각 입력 변수에 대한 미분값을 나타내는 행렬로 나타낸 것

4-4. Simplified training objective

Equation 14
$L_{simple}(\theta) \coloneqq \mathbb{E}_{t, x_0, \epsilon} [|| \epsilon - \epsilon_{\theta}(\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t) ||^2]$

• (Equation 14)와 같이 학습하면 sample quality 높아지고 구현하기 더 쉽다.
• $t$는 1~T 사이의 값이다.
• $t=1$일 때는 $L_0$에 해당한다.
• 여기서, $L_0$은 (Equation 13)에서 봤듯이 적분이 있고, 이 적분은 가우시안 확률 밀도 함수에 bin width(바이너리 폭, 구간의 길이)을 곱한 것으로 근사화되며, $\sigma^2_1$과 edge effects(가장자리 효과)는 무시한다.

가우시안 확률 밀도 함수에 바이너리 폭(구간 폭)을 곱하면, 특정 구간 내에서의 확률을 근사할 수 있습니다.

가장자리 효과는 데이터의 범위의 끝 부분에서 발생하는 왜곡이나 불완전한 정보를 의미한다. 정규분포는 평균에서 멀어질수록 이러한 효과가 충분히 발생할 수 있을 것 같다. 그래서 (Equation 13)에서 구간에 대한 새로운 정의를 정했고, 이를 통해 가장자리 효과를 무시할 수 있었던 것 같다.

• $t >1$일 때는 (Equation 12)의 가중치가 없는 버전에 해당한다.
• 이는, NCSN denoising score matching model에서 사용되는 loss weighting(손실 가중치)와 유사하다.

NCSN은 Noise Conditional Score Networks의 약자로, 노이즈 제거 및 이미지 생성과 관련된 딥러닝 모델이다.

• $L_T$는 $\beta_t$가 고정된 값이기 때문에 존재하지 않다.
  

• (Algorithm 1)은 이 간단화된 목표와 함께 완전한 학습과정을 나타낸다.

• (Equation 14)는 (Equation 12)에서 weighting을 지우기 때문에, (Equation 14)는 standard variational bound에 대한 reconstruction의 다양한 측면을 강조하는 weighted variational bound이다.
• section 4에서의 모델의 설정값들은 간단화된 목표가 작은 $l$에 해당하는 loss 값을 down-weight하게 한다.
• 이것들은 network가 매우 작은 노이즈 값에서 데이터를 denoise 하는 것을 학습하도록 한다.
• 그래서, down-weight를 통해 큰 t 값에서의 어려운 denoising 일에 집중할 수 있다. (왜냐하면, t가 클수록 데이터에 가우시안 노이즈가 더 심하기 때문이다.)

5. 주요 결과

• T = 1000
• forward process variancess는 from $\beta_1 = 10^{-4}$ to $\beta_T = 0.02$로 선형적으로 증가한다.
• 위 상수들은 [-1, 1]로 스케일링 된 데이터에 비해 작게 선택됐다.
• unmasked PixelCNN++와 유사하고, 전반적으로 그룹 정규화가 적용된 U-Net backbone 모델을 사용했다.
• 16 x 16 feature map에서 self-attention을 진행했다.

• 더 많은 사진은 글 마지막에 나온다.

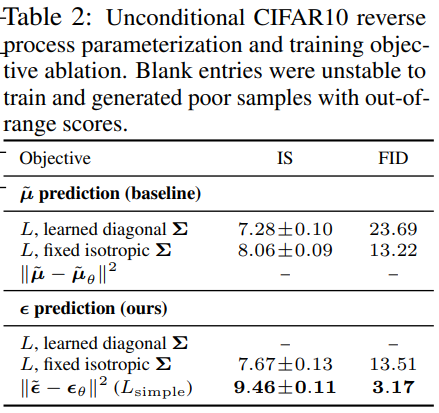
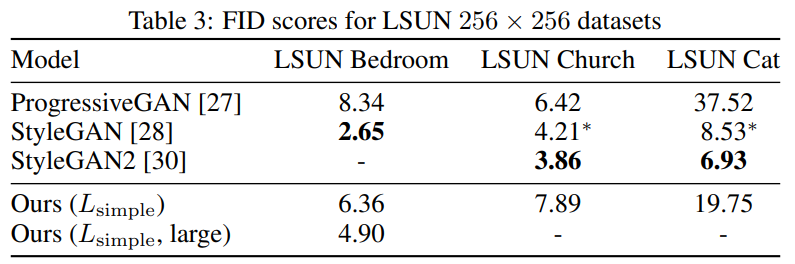
• variational bound에서의 rate를 $L_1 + \dotsb + L_T$로 하고, distortion을 $L_0$라고 할 때, 가장 높은 샘플링 성능을 가진 our CIFAR10 model은 1.78 bits/dim의 rate와 1.97bits/dim의 distortion을 가지고, RMSE(Root Mean Squared Error)를 계산 했을 때, 0~255 범위에서 0.95의 값을 가진다.

여기서 rate는 모델이 데이터를 생성하는데 필요한 평균 정보량(모델이 데이터를 얼마나 효율적으로 압축하고 있는지를 나타냄.) 즉, 높을수록 많은 정보를 담고 있다.

distortion은 생성된 데이터와 실제 데이터 간의 차이를 측정한 값. 즉, 여기서는 차원별 1.97 bits만큼의 왜곡이 발생한다는 말이다.

• (Algorithm 3, 4)는 어떤 분포 $p$나 $q$든지 평균적으로 $D_{KL}(q(x) || p(x))$ bits를 사용하면서, $q$분포에 해당하는 sample $x$(sample $x ~ q(x)$)를 전송할 수 있다.
• $x_0 \sim q(x_0)$을 적용하면, (Algorithm 3, 4)는 $x_T \sim x_0$를 순차적으로 전송하고, 이때, 예상 codelength(특정 메세지를 전송하는데 필요한 비트 수)는 (Equation 5)와 같다.
• receiver(수신자)는 어떤 $t$에서든 $x_t$ 사용 가능하고, 다음 식처럼 점짐적으로 추정이 가능하다. ($\because$ (Equation 4))

  Equation 15
  $x_0 \approx \hat{x_0} = (x_t - \sqrt{1 - \bar{\alpha}_t} \epsilon_{\theta}(x_t)) / \sqrt{\bar{\alpha}_t}$

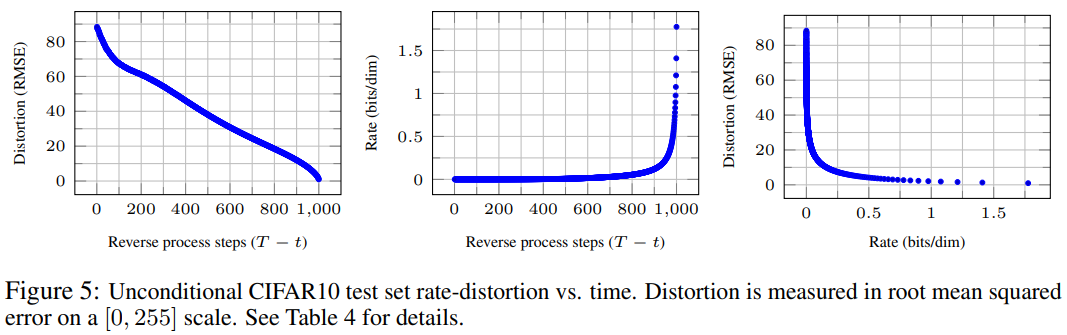
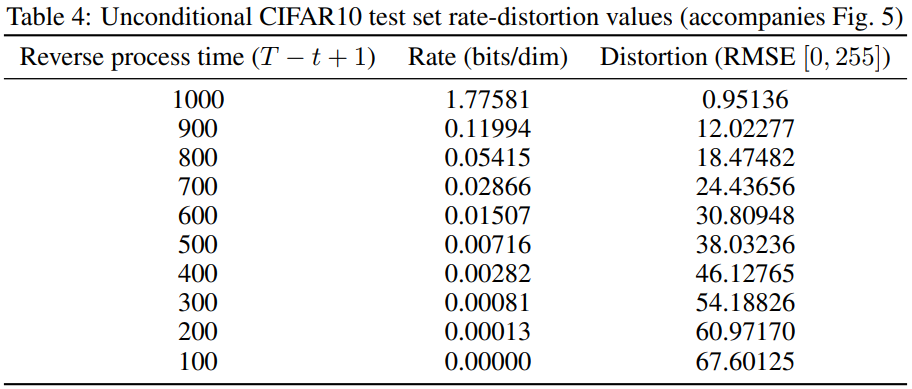
• distortion은 RMSE $\sqrt{|| x_0 - /hat{x_0} ||^2 / D}$로 계산된다.
• rate은 $t$ 시간까지 수신된 누적 비트 수로 계산된다.
• (Figure 5)를 통해서 bits의 대부분이 보이지 않는 distortion 부분에 많이 할당되었음을 확인할 수 있다.

$q(x_t | x_0)$은 처음 t개의 좌표가 가려진 상태에서 $x_0$에 모든 probability mass(확률 질량)을 할당한다.
$p(x_T)$는 빈 이미지에 모든 mass(질량)을 할당합니다.
$p_{\theta}(x_{t-1} | x_t)$는 fully expressive conditional distribution(완전한 표현력을 가진 조건부 확률 분포)가 된다.
확률 질량이나 질량은 이산 확률 분포에서 특정 사건에 대한 확률을 의미한다.

• 위와 같은 선택으로 $D_{KL}(q(x_T) || p(x_T)) = 0$와 $D_{KL}(q(x_{t-1} | x_t) || p_{\theta}(x_{t-1} | x_t))$은 $p_{\theta}$를 학습시킨다.
• 여기서 $p_{\theta}$는 $t+1,...,T$의 좌표를 변경하지 않고 복사하고, $t+1,...,T$가 주어졌을 때 $t$번째 좌표를 예측한다.
• 그러므로 가우시안 diffusion model은 autoregressive model(자기 회귀 모델)로 볼 수 있다.
  왜냐하면, 특정 시점의 값이 이전 시점의 값들에 의존한다고 가정했고, 그러므로, 현재 관측값 = 이전의 관측값의 선형 조합이라고 이해했다.

6. Comment
: 확률과 통계에 대한 공부의 절실함을 느낀다. 추가적으로 확실히 이전 논문들보다 전반적으로 계속 막히는 느낌이었다. 이 분야에 대해서 처음 접하다보니 오래걸리고 이해하는데 힘들었던 것 같다.

더 자세한 내용은 논문 원본을 참고하시기 바랍니다.

개인의 주관이 반영된 해석이라 논문의 의도와 다를 수 있습니다. 
오류가 있다면 댓글로 알려주시면 감사하겠습니다!