Conservative Q-Learning for Offline Reinforcement Learning

Introduction

Reinforcement Learning 의 목적은 MDP 상황에서 expected cumulative discounted reward 를 최대화 하는 policy 를 학습하는 것이다. Off policy RL 은 behavioral policy pi_beta (a|s) 이외에 parametric policy 또는 parametric Q-function을 maintain 하는 dynamic programming에 기반을 두고 있다. 이 parameterized Q-function 을 Bellman optimality operator 에 적용하여 exact or an approximate operator 로서 사용한다.

특히 off-policy RL 에서 자주 쓰이는 actor-critic 알고리즘에서는 policy evaluation 단계에서 Bellman operator를 통해 Q function value 를 최대화 하는 Q 를 찾고, 이를 간접적으로 활용해 앞서 사용된 policy 와 분리된 parameterized policy 를 improve 하도록 update 하는 방식으로 학습이 이루어진다.

Offline Q-Learning

실제 환경과 상호작용하며 여러 state 에 대한 다양한 action 의 결과를 학습에 사용할 수 있는 online learning 과 달리, offline learning 방식에서는 Q-function이 학습되는 과정에서 이미 기존에 샘플된 데이터셋으로부터 학습이 진행된다.

구체적으로, policy evaluation 단계에서 Bellman backup 에 사용되는 target value가 learned (parameterized) policy 로부터 샘플되는 action으로 계산되는 반면에, Q-function 이 학습되는 과정에서는 사전에 수집된 dataset 을 만드는 behavioral policy pi_beta 로부터 샘플된 “일부분의” action 으로부터 학습이 된다는 점에서 차이가 있다.

즉, Q-function 학습 과정에서는 사전에 behavioral policy 로부터 샘플된 데이터셋으로 학습이 되는 반면, policy evaluation & improvement 단계에서 사용되는 policy는 parameterized policy pi_k 로, action 이 더 다양하게, 사전에 수집된 데이터셋에서 등장하지 않은 action도 샘플될 수 있다.

바로 두 policy 가 다르다는 점에서 distribution shift 문제가 발생한다. pi 는 그저 Q-values 를 최대화하는 방향으로만 학습이 되기 때문에 pi_beta 에서 보지 못한, 절대로 해서는 안될 위험이 있는 out of distribution action 에 높은 Q value 를 가질 수 있다는 것이다. 만약 사람이 실제로 운전한 데이터가 있다고 했을 때, 실제로 선로에 박는 행동이 없었기에, pi_k 에서 우연히 선로에 박는 행동이 샘플되어 높은 Q value 가 나왔다면, 그쪽으로 굉장히 높은 Q value 가 나올 수 있는 것이다.

기존의 offline RL method 는 learned policy 에 policy constraint 를 임의로 줘서 behavioral policy 와 유사하도록 강제한다. 이 방식은 샘플링된 행동에서 아예 벗어나지 못하도록 하고, Q-function optimization 을 제한할 수 있다는 점에서 한계가 있다.

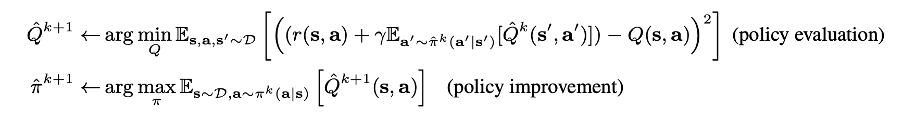
The conservative Q-learning (CQL) framework

이 방식에서는 기본적으로 policy 에 직접적인 제한을 두는 것이 아니라, 학습된 Q-function 에 따른 policy 의 expected value 가 실제 값의 lower-bound 를 넘지 않도록 설계 되어있다.

Conservative Off-Policy Evaluation

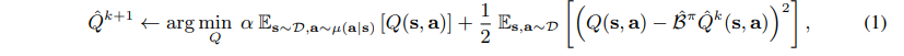
먼저 오른쪽 ½ 이 붙은 항을 보면, 이 항은 앞선 식과 다르게 s,a 가 D 즉 pi_beta 로부터 샘플된다. 이것과 더해서 왼쪽 term 을 보면 임의의 u(s,a) 라는 state-action pair 의 distribution 을 사용하는데, 이는 직접 본 데이터 (generated by pi_beta) 로부터 샘플된 데이터가 아니라 특정 distribution mu 로부터 샘플된 distribution 이다. 이 왼쪽 term 은 mu distribution 으로부터 얻은 expected Q-value 를 “최소화” 하도록 작동하는데, 이는 결국 처음 보는 action 에 대해 policy value 를 overestimation 하지 않도록 하는 penalty term 으로서 작동한다.

특히 왼쪽 term 에는 u(a|s) 가 사용되고 있는데, 이는 Q-function training 과정에서 unobserved states 로부터 Q-function value 를 얻는 것이 아니라 unobserved actions 으로부터 Q-function value 를 얻는 것이기 때문에, s 는 주어진 dataset 으로부터 가져오고 a 만 새로 샘플된다.

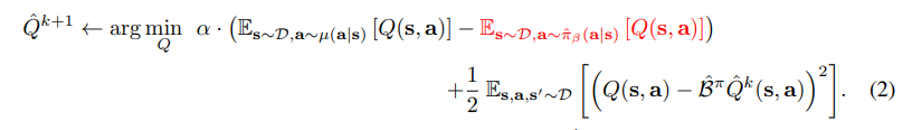
하지만 mu distribution 으로부터 생성된 action 중에는 실제로 empirical behavior distribution 의 action 과 겹치는 action 도 존재한다. 이 action 의 영향에 대해서는 그대로 받아들일 수 있도록, 즉, overestimation 을 막는 penalty 를 막도록 작동한다. (red term)

Conservative Q-Learning for Offline RL: CQL variants

policy evaluation 를 conservative 하게 하는 방법을 3.1 에서 다루었고, 본 섹션에서는 이에 이어서 policy improvement 까지 어떻게 하는지에 대한 설명을 담고 있다. 한 step 씩 policy evaluation -> improvement 를 반복할 수도 있지만 이는 연산량이 크다. 이에 대한 개선책으로, policy evaluation 에서 특정했던 mu(a|s) 를, current Q-function iterate 를 최대화 하는 policy 를 근사하는데에 사용한다. 이렇게 하면 한 번에 policy improvement 를 한 번에 진행할 수 있고, u(a|s) 에 대한 optimization problem family (online algorithm) 으로 식을 결정 지을 수 있다.

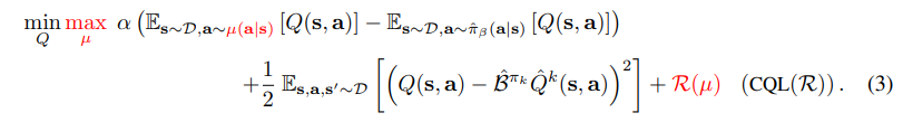
Equation (3) 의 R(u) 는 mu(a|s) 의 regularization 이다. 이와 관련해서 여러 선택지가 있는데 만약 R(u) 를, 특정 prior distribution rho(a|s) 와의 KL divergence 로 표현하면, 다음과 같은 비례관계가 성립한다. u(a|s) 비례 rho(a|s) * exp(Q(s,a)) - 이는 appendix A 에 증명됨.

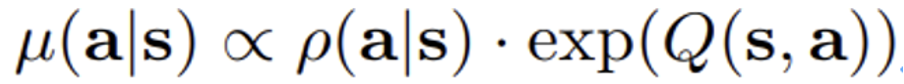
먼저 rho = unif(a) 라면(random action) Equation (3) 의 첫 번째 항은 결국 soft-maximum of the Q-values at any state s에 해당되기 때문에 단순히 아래 Equation (4) 와 같이 표현할 수 있다. CQL(H)

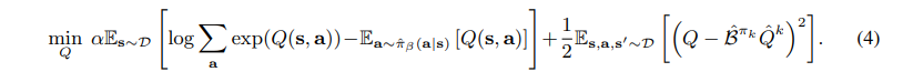
만약 rho(a|s) = previous policy pi hat k-1 라면, Equation (4) 의 첫번째 term 이 exponential weighted average of Q-values of actions from the chosen pi hat k-1 (a|s) 으로 변환된다. 실험적으로 action space 가 high dimensional 이면 후자의 방식이 더 안정적이라는 것이 드러났다.

공식 코드에서 구현된 바는 아래에 소개되어 있는 바와 비슷했다. Equation (4) 의 log sigma a exp (Q(s,a)) 부분을 계산할 때, 특히 continuous action task 인 상황에서 variance 나 computation cost 가 컸다. 그래서 CQL variant (practical version) importance sampling 을 사용해서 이를 해결하고자 하였다. 이 때 사용된 distribution 이 uniform distribution 과 current policy pi(a|s) 로부터 N개씩 (10개씩) sample 해서 이를 평균내는 방식을 사용하였다고 소개되고 있다. (Appendix F, computation part)

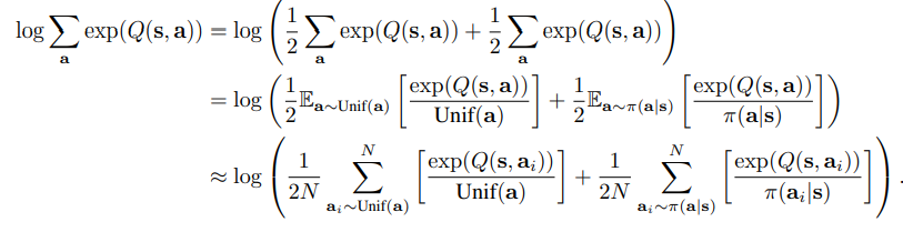
더 구체적으로 코드를 확인해보니 엄밀하게는 조금 차이가 있었다.

https://github.com/aviralkumar2907/CQL/blob/master/d4rl/rlkit/torch/sac/cql.py

https://github.com/yihaosun1124/OfflineRL-Kit/blob/main/offlinerlkit/policy/model_free/cql.py

random action, current action 으로부터 Q 구한 것 뿐만 아니라, next action 으로부터 Q 구한 것도 concatenation 이 되어있었다. 이는 Appendix F 의 Choice of Backup 에 관련 내용이 소개되어 있는 것으로 생각된다.

Total Algorithm

theta는 Q Function 모델의 매개변수, phi는 Policy 모델의 매개변수를 나타낸다. 각 Q Function, Policy 매개변수를 초기화한 이후에, G_Q Gradient Step만큼 CQL Objective Function을 적용한 Q Function 학습을 진행한다. 그 다음, 만약 actor-critic 방식을 활용한다면, G_phi Gradient Step만큼 Soft Actor Critic의 Entropy Regularization을 활용한 Objective Function을 적용하여 Policy 모델에 대한 학습을 진행한다.

Results

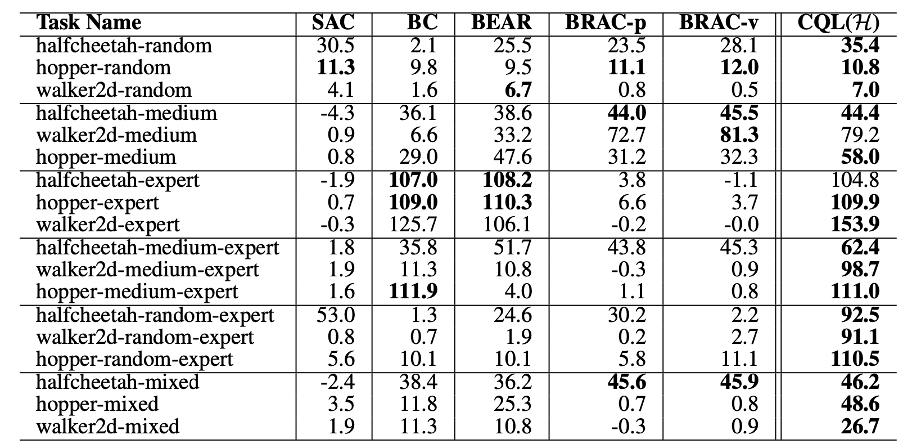
Mujoco dataset 에서 다음과 같은 성능을 기록했다. 다만, 이 dataset 은 version1 이고 타 논문에서 새로 공개된 version2 dataset 에 대한 성능이 재현, 기록되었다.

Discussion (limitation and future work)

저자는 논문의 한계와 앞으로의 방향성으로 두 가지를 언급하고 있다.

• 여러 approximation case 에 대해 CQL 이 Q-function 의 Lower bound 가 될 수 있음을 증명했지만 rigorous theoretical analysis with DNN 이 향후 필요함.
• offline RL method 는 supervised learning 과 같이 overfitting 문제를 겪을 수 밖에 없으므로 이 또한 앞으로 풀어야 할 과제임.

향후 등장한 논문에서는 CQL 에 대해 몇몇 좋게 판단할 수 있는 Q function 에 대해 너무 pessimistic 하게 평가할 수 있음을 언급하고 있기도 하다. 실제로 이후 등장한 논문은 lower bound 보다는 좀 더 pessimism 을 약화한 버전의 방법을 제안하기도 하고, offline RL 의 distribution shift 의 원인이 되는 OOD action 자체를 sampling 하지 않는 방식을 제안하기도 한다.