Offline Reinforcement Learning with Implicit Q-Learning

Implicit Q-Learning (IQL) 은 시기상 CQL 과 MCQ 사이에 나온 논문이다. 결론적으로 봤을 때 MCQ 의 방식과 유사하지만 motivation, 논리를 전개하는 방식, 사용하는 model 등에서 MCQ 와 구분되는 차이들이 존재한다.

Introduction

저자는 offline RL 이 겪고 있는 distribution shift 문제를 언급하고, not seen in data 인 action 을 애초에 query 하지 않고 optimal policy 를 학습하는 방법을 제안하였다. 이 방법의 핵심은, given state 에 대해 in-distribution action 과의 Q function 의 upper bound 를 expectile regression 을 통해 추정하는 것이다.

Preliminaries

offline RL method 는 아래와 같은 loss 를 통해 Q network 를 학습한다.

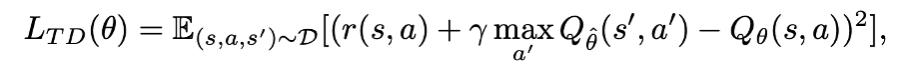
특히 value function loss 를 수정해 value function 을 regularize 하여 resulting policy 를 data 에 가깝도록 제한을 둔다거나 arg max policy 를 강제하는 방식을 사용하는데, 이 방식은 OOD action 에 대한 overestimation 을 초래해 학습을 저해할 수 있다. CQL 에 대해서도 언급하고 있는데, 이 방식에는 distributional shift 로부터의 misestimation 을 막는 만큼 기존의 policy 가 improve 될 수 있는 가능성을 낮추는 trade-off 관계가 존재한다 언급하고 있다.

Implicit Q-Learning

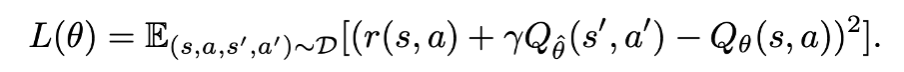
이 방식은 expectation (s,a,s’,a’)~D 를 보면 알 수 있듯이 기본적으로 OOD sample querying 을 avoid 하여 simply pi_beta (behavior policy) 를 학습하는 전략을 취한다. 그렇기 때문에 만약 모델의 capacity 도 충분하고 sampling error 도 없는 가장 이상적인 환경에서는 아래와 같은 관계가 성립할 것이다.

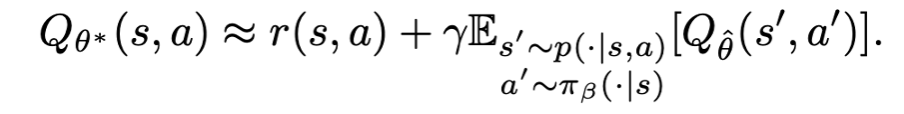
Offline RL Without Off-Policy Evaluation 를 포함한 이전 연구에서 위에서 언급한 OOD sample 을 제외하고 데이터셋에서만 학습을 한 연구가 존재하긴 했다. 하지만 이 방식을 사용했을 때 multi-step dynamic programming 으로부터 문제를 해결해야 하는 복잡한 task 에는 굉장히 poor performance 를 보인다고 언급하고 있다.

이 문제를 보완하기 위해서 아래 식과 같이 (s,a,s’)~D 까지 샘플하되, pi_beta 에서 가능한 action a’ 의 Q function 중에서 “최대”가 되는 Q value 추정치를 loss term 에 활용한다. 이는 CQL 이나 MCQ 에서 사용하는 N sampling 방식 후 평균을 내는 것이 아닌 뒤에서 설명할 expectile regression 이라는 방식을 통해 이루어진다.

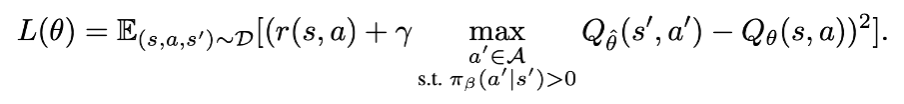
Expectile Regression

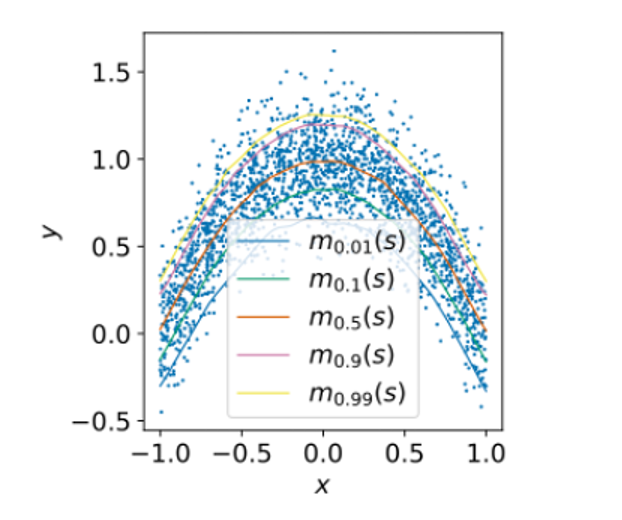
expectile regression 은 tau 라는 미리 정해진 hyperparameter 에 따라 mean regression 이외의 다른 quantile (expectile) 의 statistics 를 추정할 수 있는 framework 이다. 기본 식은 아래와 같다.

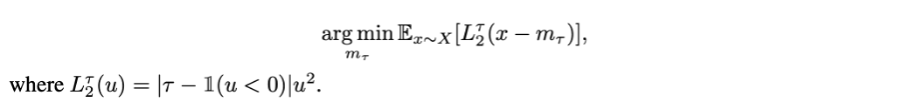
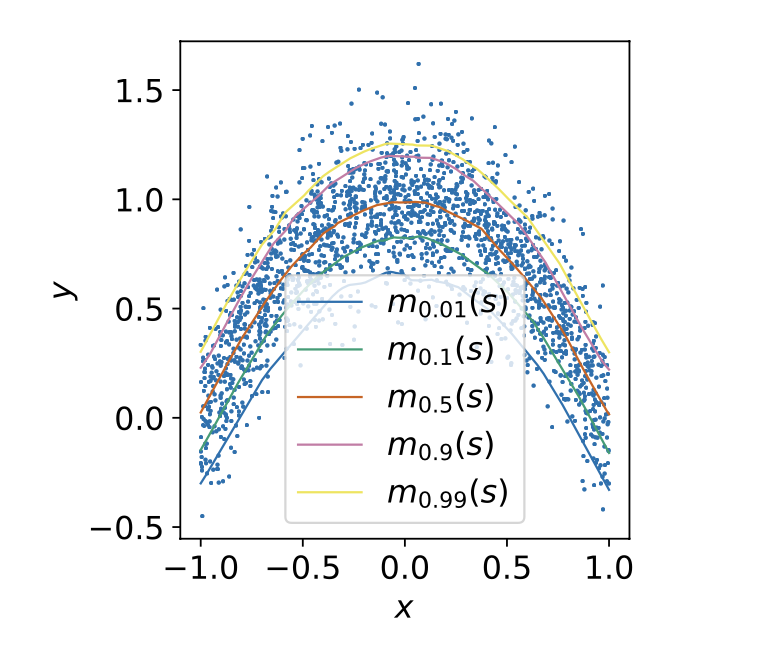
여기서 m_tau 는 x 의 추정치이다. 만약 tau=0.99 라고 가정해보자. 0.99 라면 indicator(u<0) 에 의해 x > m_tau 즉 추정치가 x 보다 작으면, indicator function=0 이 될 것이고, u^2 값에 0.99 라는 큰 weight 가 곱해지게 될 것이다. 반면에 x < m_tau 즉 추정치가 x 보다 큰 경우에 indicator function=1 이 될 것이고, u^2 값에 0.01 이라는 작은 weight 가 곱해지게 될 것이다. 이 문제는 결국 minimization problem 이기 때문에, 추정치는 대부분의 x 보다 크도록 fitting 이 될 것이라 예상할 수 있다.

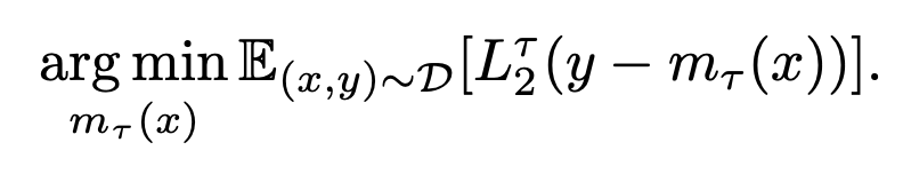
위와 같이 x 에 대한 y 값 추정에도 비슷하게 적용할 수 있다.

Learning the Value Function with Expectile Regression

이를 그대로 offline RL 문제에 적용해 “최대”의 Q value 를 추정하는 모델링에 사용할 수 있다. 이를 식에 적용하면 아래와 같이 쓸 수 있다. 즉 TD target 의 upper expectile 을 예측하기 위해 policy evaluation objective 를 아래와 같이 수정한 것이다.

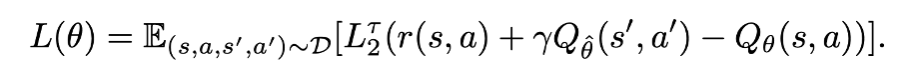
하지만 이 방식에는 잠재적인 문제가 있다. 이는 environment dynamic (transition) 에 의해 s,a 가 선택되고 s’ 이 선택된 뒤에 Q(s’, a’) 이 “높게” 계산되었을 때, 이 값이 운좋게 좋은 s’ 이 선택되어서 Q 값이 높게 나온 것인지 아니면 action’ 이 잘 선택되어서 Q 값이 높게 나온 것인지 분리할 수 없다. 이 문제를 해결하기 위해 분리된 value function model 을 도입한다. 따로 action distribution 에 대해서만 expctile 을 근사하는 모델을 새로 도입하면 아래와 같이 쓸 수 있다.

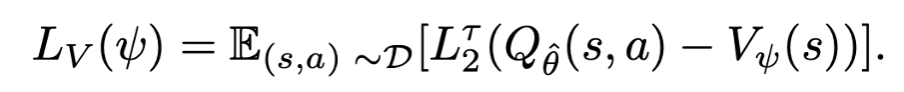
이 value function model 로 state 를 평가하고, 이 평가한 값을 다시 아래 Q function 모델과 함께 사용하면 environment dynamics (transition) 에 의한 효과를 average 하고 언급한 lucky sample issue 문제를 완화할 수 있다.

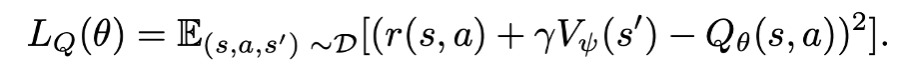
실제 코드 implementation 을 보면 critic Q function model 이외에 새로운 parameterized Critic value function model 을 추가로 사용한다.

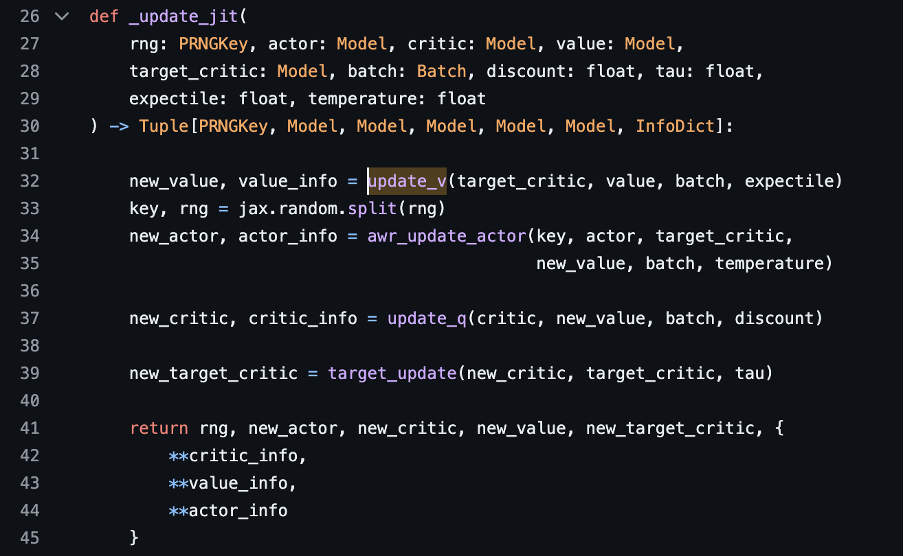
https://github.com/ikostrikov/implicit_q_learning/blob/master/learner.py

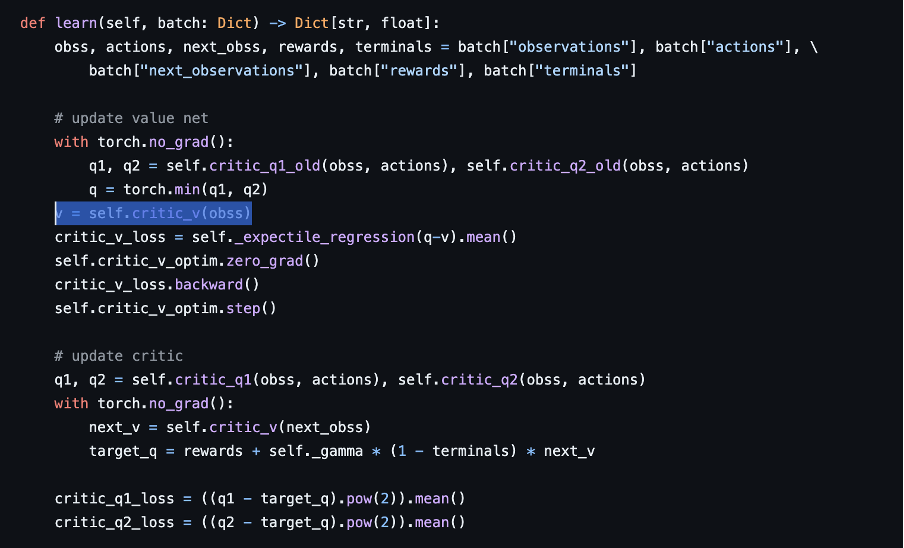
https://github.com/yihaosun1124/OfflineRL-Kit/blob/main/offlinerlkit/policy/model_free/iql.py

마지막으로 실제로 action selection 을 진행하는 actor model 에 어떻게 값을 전달할지에 대한 내용이 설명되고 있다. 다른 모델들과 비슷하게 critic model 의 결과값과 actior 가 selection 한 모델의 차이를 loss term 으로 구성하고 이를 backpropagation 하는 구조이다. 특히 beta 라는 inverse temperature 를 사용한 AWR (advantage - weighted regression) policy extraction 방식을 사용하고 있다. beta가 클수록 behavioral cloning 을 하기보다는 Q-value 를 maximization 하는 방향으로 objective 가 행동한다. task 마다 다른 값을 사용하고 있다. (beta = 3 for Mujoco, beta = 10 for Ant Maze)

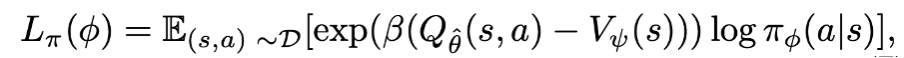
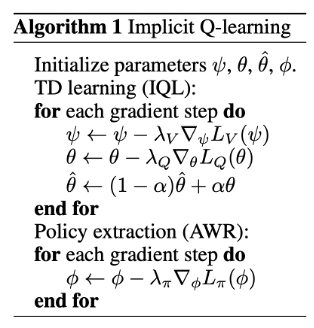
Algorithm Summary

마지막으로 언급했던 value function model, q function model 을 활용한 Q-learning 과정을 요약해서 나타내고 있다.

Results

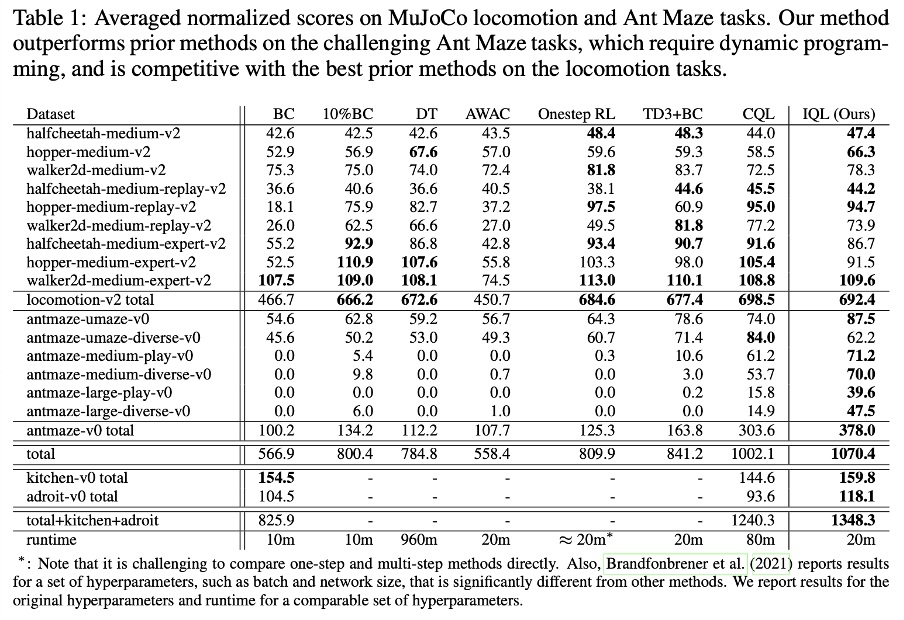
모든 mujoco task 에 대해 과거 baseline 방식들보다 성능이 잘 나온 것은 아니지만, 그에 준하는 성능을 기록했고 몇몇 방식은 mujoco task 에만 초점을 맞췄던 반면에 IQL 은 다른 task 들에 대해서도 좋은 성능을 기록했다고 언급하고 있다. 또한 maze trajectories 에서 성능이 잘 나오기 위해서는, “stitching” parts of suboptimal trajectories 가 필요하다는 선행 연구결과를 언급하며 IQL 에서 이러한 경향을 보이고 있다고 언급하고 있다.

Discussion (limitation and future work)

저자는 논문에서 명시적으로 연구의 한계점과 향후 연구 방향에 대해 언급해 놓은 부분은 없었다. 이와 관련해서 추가적으로 논문 조사를 했고, IQL 을 LLM 에 적용한 연구 (ILQL) 에서 연구자의 의견을 읽어볼 수 있었다.특히 AWR policy extraction 과 관련해서, pi_beta 에서 자주 sample 되지 않지만 over-smoothed 되는 pi_beta distribution 특성 상 erroneous high Q or V value 를 가지는 경우가 있을 수 있다고 언급하고 있다. 즉 자주 등장하지 않는 sample 에 대해 over-estimation 할 위험이 있다고 언급하고 있다. 이에 ILQL 저자는 추가적인 CQL regularizer 를 추가해서 이런 문제를 완화하고자 했다고 언급하고 있다. 이것 이외에 expectile regression 에 사용되는 tau 값이나 앞서 언급했던 beta 와 같은 hyperparameter 를 task 마다 일일히 fine-tuning 해야 한다는 한계점이 존재한다. 이러한 문제들을 해결하기 위한 향후 노력이 필요할 것으로 생각해 볼 수 있다.