[Paper Review] DTFD-MIL: Double-Tier Feature Distillation Multiple Instance Learning for Histopathology Whole Slide Image Classification
Paper Review
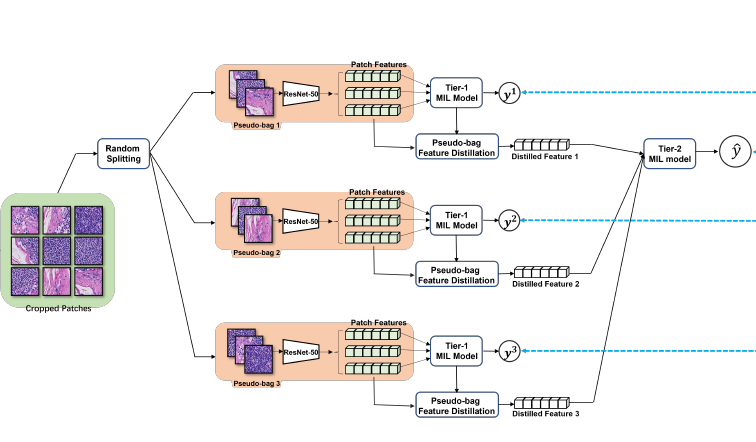
DTFD-MIL: Double-Tier Feature Distillation Multiple Instance Learning for Histopathology Whole Slide Image Classification
특정 dataset 에 대해, MIL SOTA 칭호를 얻은 논문이다. 다른 논문에서 SOTA 로써 인용되기도 하고 아이디어도 reasonable 해보이고 코드도 공개되어 있어서 가져다 써보려 한다. (이미 누가 돌려봤다) 핵심 아이디어는 psudo-bag 을 통해 number of bag 을 늘린 것, 늘려 발생한 문제를 완화하기 위해 double-tier 구조를 착안한 것에 있다.
Introduction
- WSI 분석과 MIL 등장 배경
- ABMIL 관련 서술
- instance probability inference 가 infeasible 하다 여겨져 왔고, 차선책으로 attention score 를 사용해옴.
- 본 논문에서는 ABMIL framework 에서 instance probability 를 derive 함.
- mutual-instance relation 과 over-fitting problem 간에 trade-off 가 있음.
- negative impact 를 완화하기 위해 pseudo-bag 을 만듦.
- 이로부터 발생하는 risk 를 완화하기 위해, Grad-CAM 을 활용한 double-tier MIL 구조를 고안함.
Method
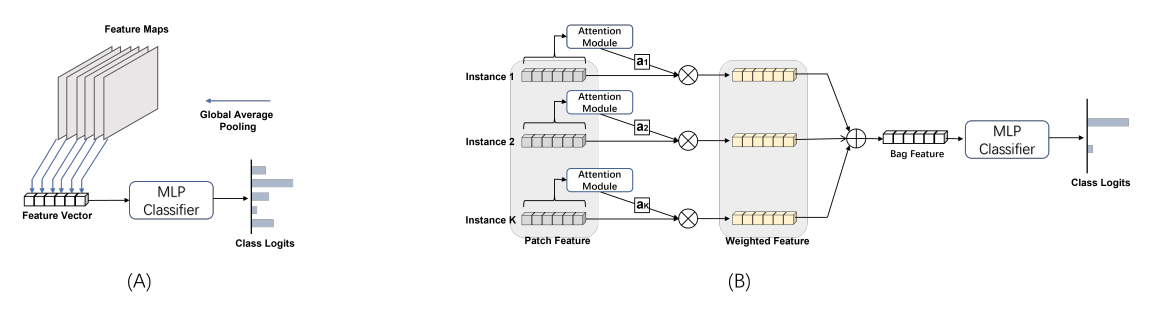
Revisit Grad-CAM and AB-MIL
Grad-CAM
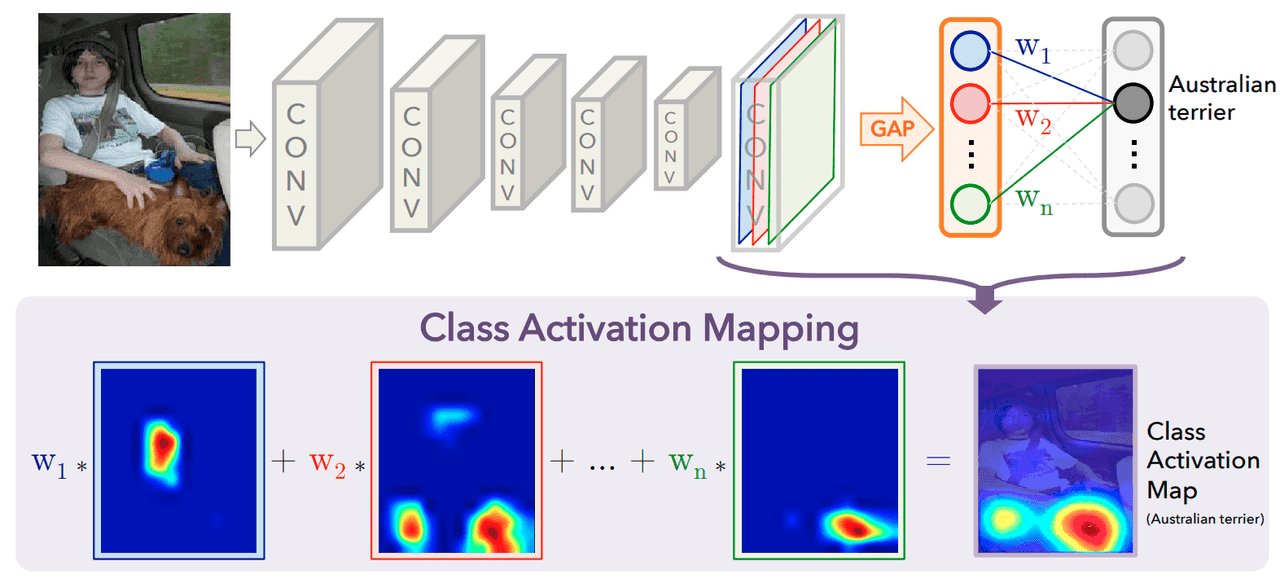
end-to-end image classification 에서 DCNN 의 high level feature map DxWxH (D: number of channel, W,H dimension)을 global average pooling 을 거쳐 channel D dimension 을 가진 feature 를 얻는다. 이 때 f 를 MLP 에 통과시키고 logit for class c (1,2,...,C) 를 얻는데, 아래 식을 거쳐 Grad-CAM의 class activation map 을 얻을 수 있다.
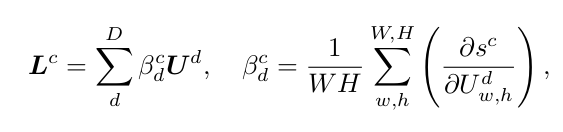
즉, softmax 와 input f 에 의해 결정된 signal strength 로써 image 가 각 class C에 해당할 probability 를 계산하고, 아래 식과 같이 특정 위치에서 특정 class 에 대해 얼마나 신호가 강한지를 나타낼 수 있게 된다.
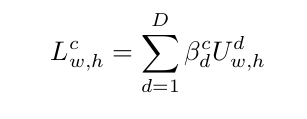
Attention-Based Multiple Instance Learning
앞선 포스팅에서 많이 언급되었던 내용이라 간단히 수식들만 언급하도록 하겠다.
Bag label - bag representation, bag classification task
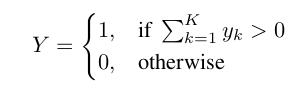
is an aggregation function, : extracted feature for instance
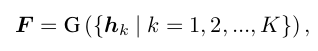
learnable scalar weight for , D: dimension of vector and
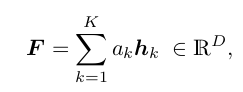
weight from the classific AB-MIL, where are the learnable parameters
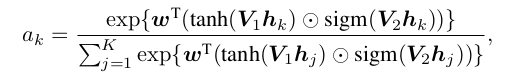
Derivation of Instance Probability in AB-MIL
본 논문에서 핵심 내용 중 하나이다. 위에서 언급해왔듯 attention score 을 class probability 로 대신 사용해왔고, 이를 극복하고자 AB-MIL framework 가 가지는 특수성을 기반으로 individual instance 의 predicted class probaility 를 유도한다. 다음 proposition 위에서 derivation 이 이루어진다.
Proposition 1 The paradigm of AB-MIL is a special case of the framework of the classic deep-learning network for image classification
supplmentary 에 proposition1 의 증명과 설명이 있다. 저자의 논리는 이 proposition 1 에 기초하여, Grad-CAM 의 mechanism 을 AB-MIL 에 바로 적용하여, 각 instance 의 signal strength 를 Grad-CAM과 같이 derive 할 수 있다고 한다.
supplementary 의 증명이라고 하기엔 애매한 설명은 다음과 같다.
- : AB-MIL 은 averaging pooling 으로 볼 수 있다.
- : deep learning 에서의 GAP도 다음과 같이 쓸 수 있다
- deep learning 과 MIL 모두 넓게 보면 classification problem 이다
- F 와 f 의 유일한 차이는 spatial relation 이 F에는 고려되지 않았다는 점이다.
- 하지만 Grad-CAM 에서 attention map inference 는 spatial relation 이 아무 역할을 하지 않는다
- 그러므로, DCNN 에서 signal strength 를 나타내는 Grad-CAM 식 처럼
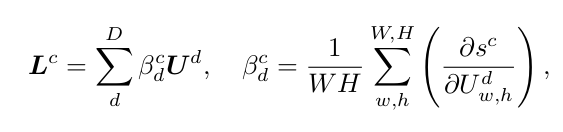
- AB-MIL 에서 각 instance 의 signal strength 나타내는 Grad-CAM 식을 아래처럼 쓸 수 있다
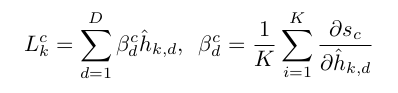
보면, U 가 h 로 바뀌었고, 는 output logic for class c from MIL classifier 이다. 이 식에 softmax 를 적용하여 p를 구한다.
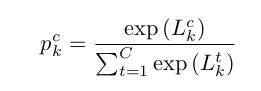
supplementary 에 나온 설명을 덧붙이자면, 이 식은 instance 가 large enough attention score 를 가지고 있을 때만 유효한 값을 가진다. 그 이유는, certain patch 가 attention module 에서 deactivate 되어 값이 0에 가까워지면, 그에 해당하는 도 0에 가까워지고, 이에 따라 는 모든 class에 대해 0, 는 정보량이 없는 0.5에 가까워 질 것이기 때문이다. 이런 점 때문에 pseudo-bag 을 만들고 attention score 에 따른 patch selection 사전작업이 이루어 졌다는 점을 언급하고 있다.
Double-Tier Feature Distillation Multiple Instance Learning
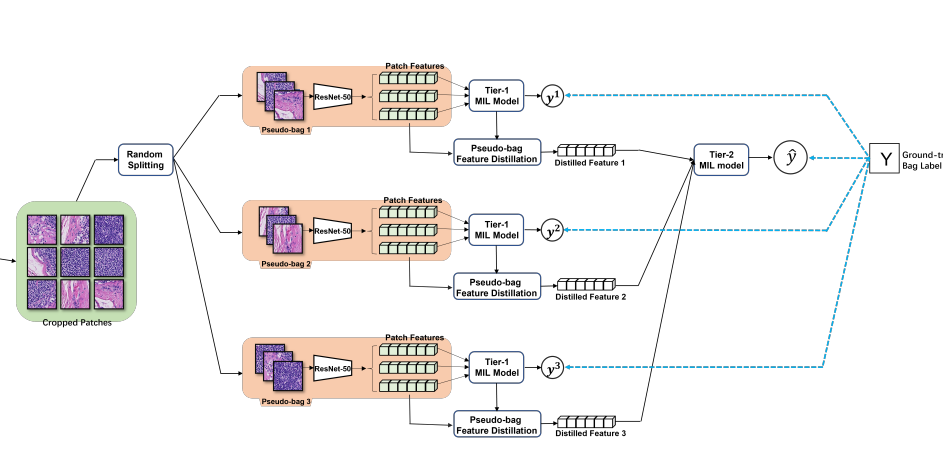
double-tier feature distillation MIL framework 에 대해 자세히 언급한다. 여기부터는 크게 어려운 부분은 없다. 다만 notation 이 많아서 좀 헷갈린다. 그림 보면서 보자.

- Given N bags (slides), each bag there are Kn instances (k=1,2, ..., Kn), (n=1, ..., N)
- i.e., with ground truth of bag
- feature of a patch, denoted as
- randomly split into pseudo-bags,
- inTier-1 model (AB-MIL model), estimated bag probability of pseudo-bag:
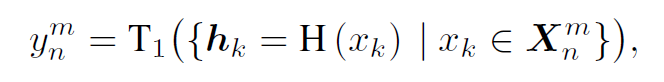
- loss: cross-entropy L1
- in Tier-2, feature from each pseudo-bag is distilled, as
- 이때, 참고로 pseudo-bag m개에서 나온 feature 가 aggregation 되었다.
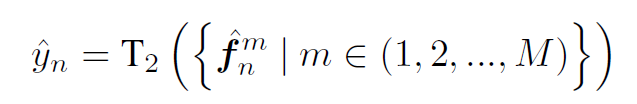
- 이 또한 cross-entropy L2
- overall optimization process 는 L1+L2 꼴
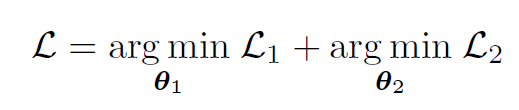
- aggregation function 은 다음 4가지로 구성됨
1) Maximum selection
2) Maximum & Minimum selection
3) Maximum attention score selection
4) Aggregated feature selection (attention 써서)
Experiments
Datasets
two public histopathology WSI dataset
- CAMELYON-16
- TCGA lung cancer
- OTSU tissue, non-overlapping 256x256 patch on 20X mag, 3.7M + 8.3M patches
Performance comparison with existing works
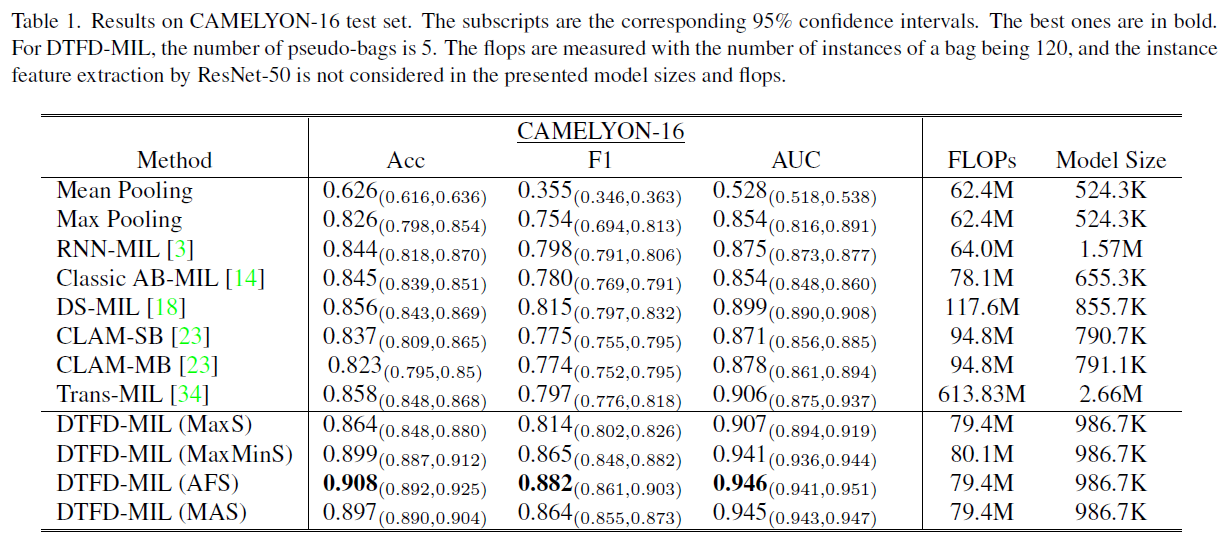
CAMELYON-16은 대부분 슬라이드에서 small portion of tumor 이고, MaxS 방식이 가장 inferior 했지만 여전히 다른 모델에 비해서는 성능이 좋았다. DTFD-MIL (AFS) 는 4% better on AUC.
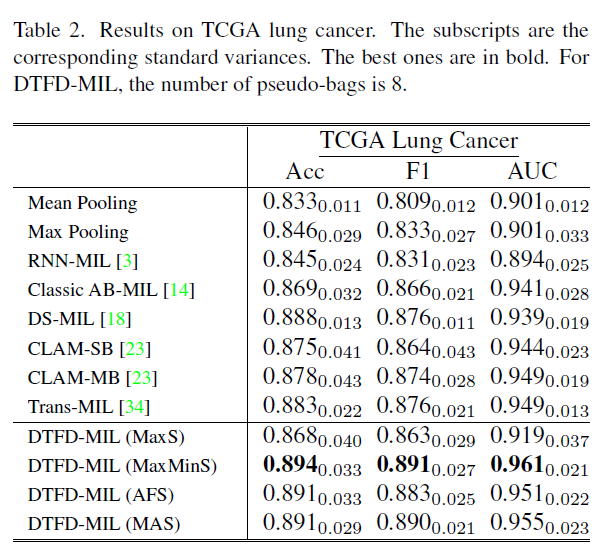
TCGA-lung cancer 에서 AUC 96.1% 를 보여주었다. 여기선 attention 을 쓰지 않은 instance-level feature 의 MaxMinS 방식에서 성능이 제일 높았는데, 이를 TCGA 의 large tumor region 가 원인이라 설명한다.
Visualization of Detection Results
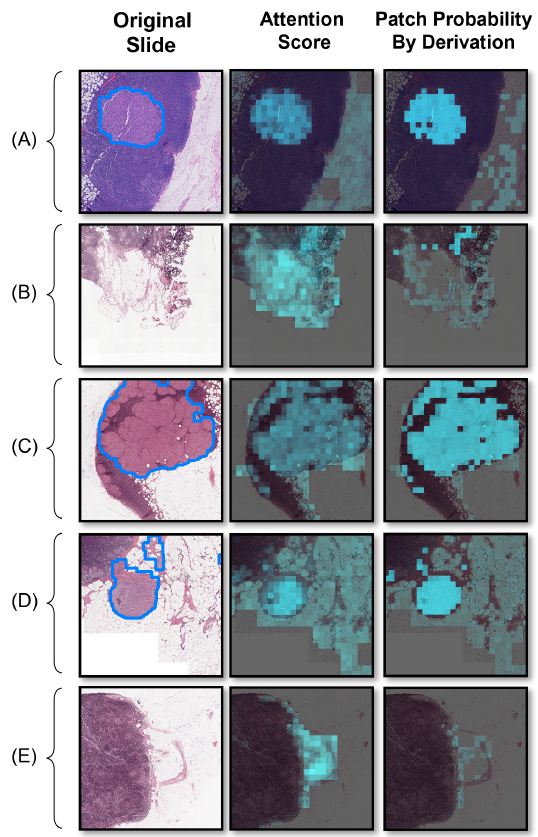
오호 Grad-CAM probability 써서 그런지 확실히 기존 attention score 쓰던거보다 낫다.
논문에서도 비슷하게 얘기한다.
Conclusion
- derivation of instance probability under framework of AB-MIL
- qualitatively demonstrate the derived instance probability was more reliable
survival 에 붙여서 빨리 코드 돌려봐야 하는데...
다른 장기에서도 통했으면 좋겠다.
