Decision making, motor task 관련해서 고대의 (2000년대) 국룰 논문을 간단히 정리한 내용이다.

Decision making, movement planning and statistical decision theory

• formulate behavioral task in language of statistical decision theory
• (traditional) misrepresent probability of rare event, fail to maximize gain
• strategy that maximize expected gain → implication: uncertainty & how information about uncertainty is acquired in motor and economic tasks

Motor tasks equivalent to decision making under risk

• (머리에서 일어나는) decision making task 를 (측정 가능한) motor task 와 비교 가능
• 2003년 논문 실험 결과를 주로 활용하고 있음
• decision task in motor form 에서, participants 가 gain 을 최대화 하는 visuo-motor plans 를 선택하고 있음을 발견함.

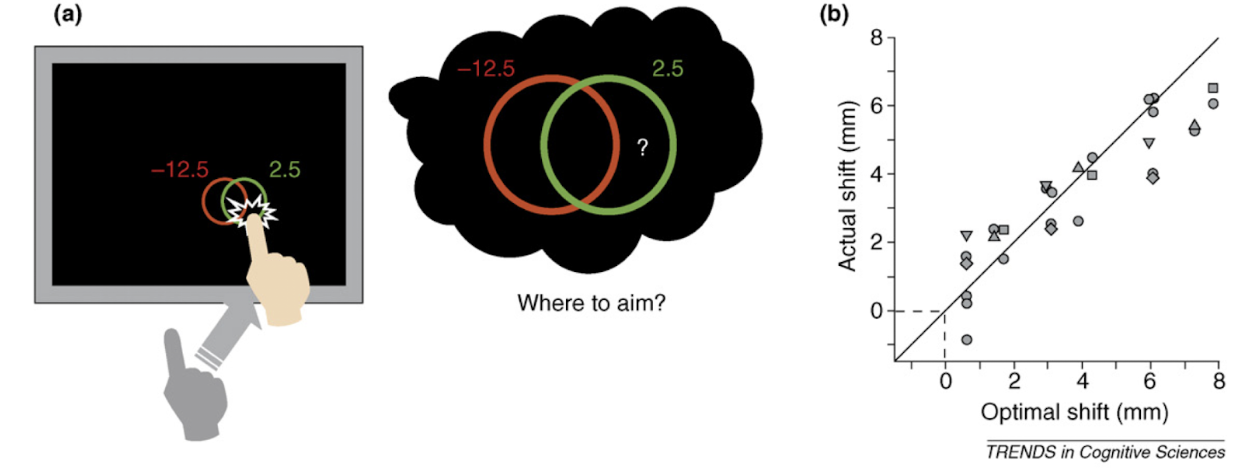
• optimal shift 즉, 빨간색 negative gain 이 커질 때마다 maximize contour 는 오른쪽으로 쏠리게 되는데, 이에 따라 실제로 사람도 오른쪽으로 터치가 쏠리게 되더라.
• (traditionally) 이전 접근은 biochemical stress (근육, 관절 스트레스) 를 최소하는 최적화 문제로 바라보았는데,
• 저자는 이러한 방식이 “externally imposed rewards and penalties” 를 반영할 수 없다고 봄.
• 하지만 그렇다고 해서 항상 maximize expected gain 하도록 movement planning 하는 것은 아님
  → 연구결과 3개 38, 39, 8 인용하며 future work 언급

Learning probabilities versus practicing the tasks

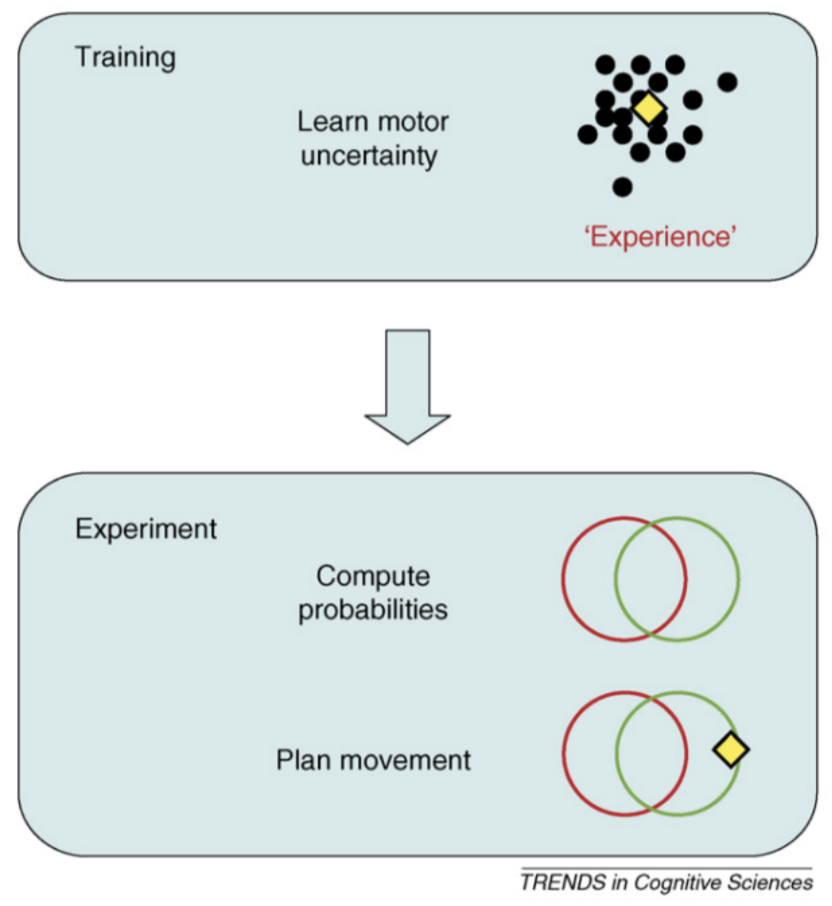
• train: speed motor task 반복 (stabilization 할 때까지.) 이후 residual motor variability 측정
  ??? 그리고 이는, no obvious trend. → “경험을 통해" modify their strategy
• 간단한 강화학습 시뮬레이션을 돌리면, log 함수처럼 trial 에 따라서 gradual 하게 증가했어야 할 optimality 가, 실제로 사람이 하면 “immediately” changed the aim point
• 맨 처음에 own motor uncertainty 를 배울 때는 gradual 하게 optimal 해졌는데, new situation 이 되었을 때는, 또 gradual 하게 처음부터 학습하는 것이 아니라, 앞에서 한 uncertainty 를 그대로 사용함.
• decision making 에서는 have perfect knowledge of how their choice changes the probability of attaining each outcomes.
• 반면, motor task의 knowledge는 explicit하게 전달되지 않기에, 같을 순 있어도 절대 decision making 의 knowledge 를 뛰어넘을 순 없음.
• 이 때, motor task 에서의 ‘lack of learning’은: 사람이 각 outcome 에 대한 probability 를 추정할 수 있음을 가리킴. 농구공을 골대로 넣었을 때 손에 남아있는 감각과 눈으로 대충 들어갈지 말지를 추정할 수 있는 것처럼..

Statistical decision theory: future directions

• visuo-motor and economic decision-making tasks can be translated into a common mathematical language. (이 내용은 refer 논문에서 좀 더 잘 설명하고 있는 듯)

Statistical decision theory and the selection of rapid, goal-directed movements

• movement planning model (MEGaMove) 가 잘 되는지 두 가지 실험
• 컴퓨터 스크린에서 리워드, 페널티 존 터치하는 실험 두 가지 종류.
• 각 실험에서, penalty 세기 / overlap 정도 / penalty region 개수 달리함. → 잘 됨

Introduction

• 간단한 decision making intuition, hook
• MEGaMove 는 action under risk 모델임. (maximize expected gain in its selection of movement strategies)
• 과거 “motor planning” 는 biochemical cost 를줄이는 single deterministic trajectory 강조. execution of the motor plan 과정 error 설명 X, not predict the goal posture (location, why the movement should arrive in certain time window?)
• 목적: may involve “aspects” other than accuracy
  monetary penalty 는 can alter the motor plan (이것이 variability 늘릴지라도)
  이 variability 는 “landscape” of penalties 를 결정하고 이 lop 에 따라 움직임 결정.
• 즉, optimal selection 을 설명하기 위해서, MEGaMove 는 extrinsic cost with the task 와 subject’s own motor variability 를 함께 봄.

A statistical decision-theory model of pointing movements

설명을 잘해주고 있음
1. motor strategy: S selection of the mean movement end point within a given time limit
2. movement trajectory. (τ : t → [x,y,z])
3. P(τ|S) : probability density. S strategy 가 결정되었을 때, 실제론 이 density 에 의해 actual trajectory 가 결정됨. RL theory 에서 state transition matrix 느낌. 근데 이걸 구하기 어려움
아마 중요한 부분: 근데 알기만 하면 구하기까지의 자세한 과정은 무시할 수 있음.
→ 이것..을 learn 할 수 있다는 것인가…
4. gain: Ri, i=0,1,2, ,,, N (region에 속하면 그 region에 대한 reward
5. Expected gain function of the motor strategy S

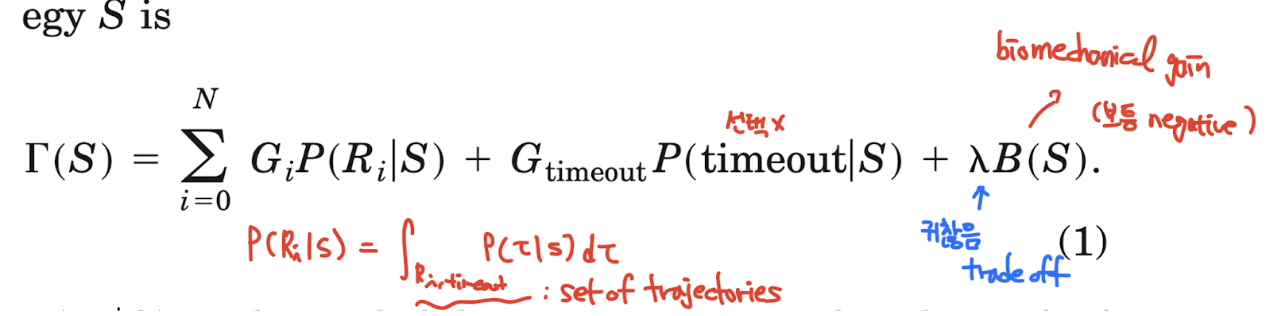
이 때, P(Ri|S) 는

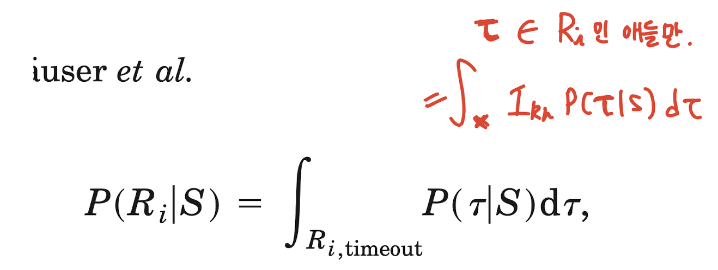
6. optimal visual-motor strategy S 는 expected gain 를 maximize 하는 것.

Example: Selecting the optimal movement end point in a landscape of expected gains

• 위 expected gain 식에서, constant 항은 빼고, P(Ri | x,y) 에 Gaussian distribution 씌워서 정리하면 다음과 같은 시뮬레이션 (?) 결과를 얻을 수 있음.

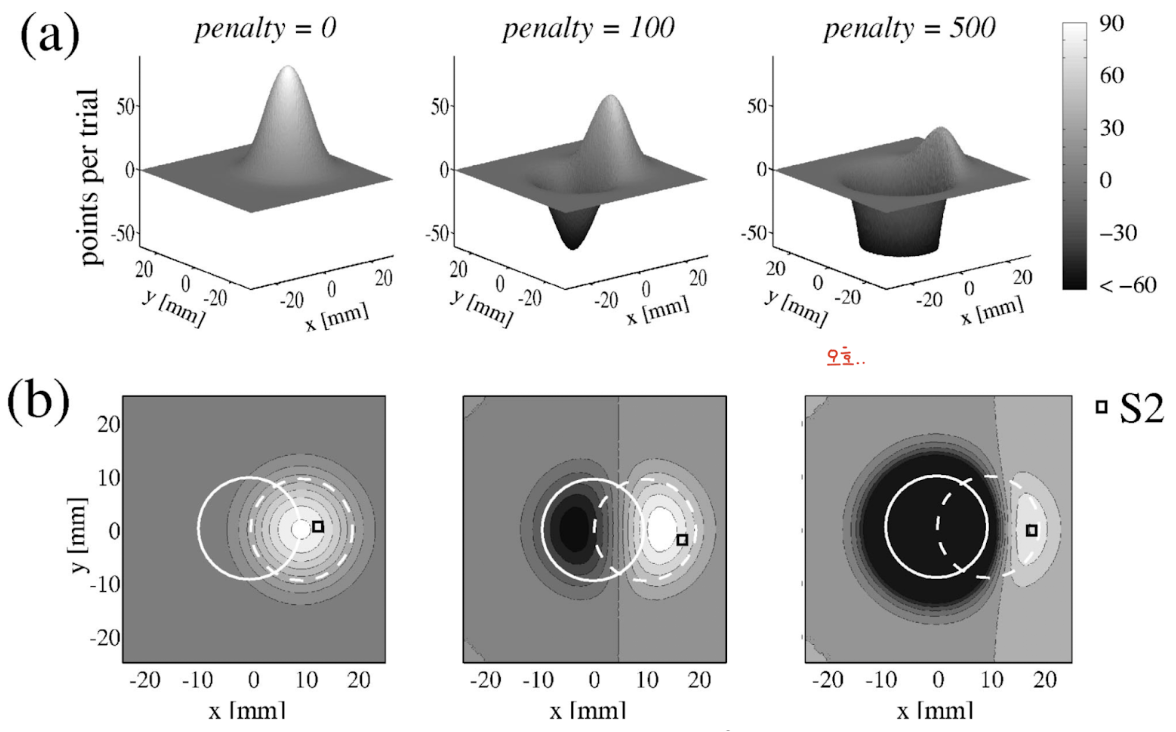
• 이 때 Gaussian distribution의 sigma 는 spatial motor variability of the subject’s response 임. vertical - horizontal 하게 같다고 가정함… (손가락으로 누르는거니까 오른손 잡이는 오른쪽 아래 부분의 uncertainty 가 더 강하거나 하지 않을까?)

Experiment1

• 실험 1, penalty red region 원을 기준으로, 오른쪽/왼쪽 각각 3개의 displacement (j) 6개, penalty value condition (i) 3개, 그리고 각 trial p (p=1,...,n_ij).
• Xmeg, Ymeg: model computation 결과 penalty region center point 에서 떨어진 정도
• xmeg, ymeg: model computation 결과 green target region center point 에서 떨어진 정도

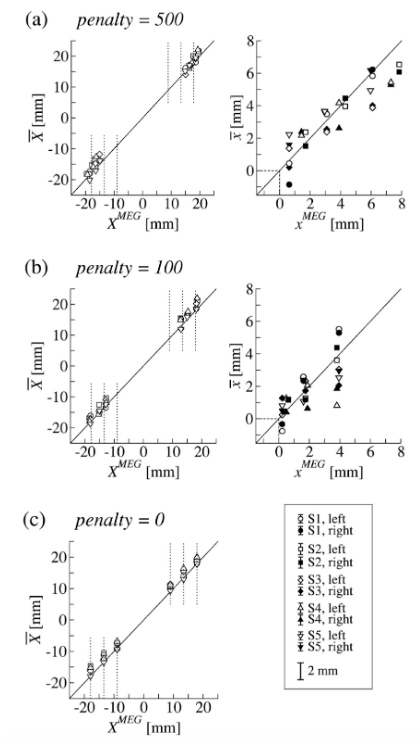
• 45-deg solid line, penalty 크면 클수록 더 shift 됨.
• regression 하고 두가지 hypothesis 로 p-test 진행. 1) 0 vs alternative : 통과
• slope is precisely 1 versus alternative : 2명 중 5명에게서 rejected null hypothesis.
  2명 slope <1 이었는데, 이는 red penalty zone 을 상대적으로 덜 두려워했다로 해석가능.
• performance 와 관하여.
  motor variability 가 높을수록 더 놓쳐서 낮은 점수를 획득했을 것.

Experiment2

• 실험2, rotation 으로 했고, 4개는 penalty zone 한개, 4개는 penalty zone 두개 있음.
• 이번에도 모델이 예측한 것과 일치하도록 나옴.
• 또한, 이전 실험에서 보였던 motor variability 와 비슷한 경향성을 띔.
• 또, penalty 를 더 복잡하게 준다고 해도 motor variability 에 영향을 주지 않음. 즉 variability 는 execution of the motor command 때문일 가능성이 높음 (rather than movement plan)

++ 한시간 연습하고 variability stabilization 후에 experiments 사이에 no practice trial 임에도 variability 안정적이었음. 이는 그 연습시간 동안 subject acquired motor variability.
++ time limit 이나 task complexity 가 증가함에 따라 model 을 깰 수도 있음.