생존 분석
생존 분석(Survival Analysis)은 대상을 관찰하며 시간이라는 변수와 함께 어떤 사건의 발생 확률을 추정하는 통계 분석 방법이다. 예후 예측부터 고객 이탈 분석 등 다양한 분석에서 활용된다.
생존 분석을 공부하다보니 오개념이 생길 여지가 많은 것 같아 시점마다 내가 어떻게 이해하고 있는지를 기록해두기 위해 글을 작성하게 되었다. 이번 포스트에서는 여러 블로그의 글과 책을 참고하여 생존 분석의 기본 개념을 정리할 것이다.
생존 분석의 기본 개념
위에서 생존 분석을 확률 개념으로 간단히 정의했는데, 조금 더 쉽게 쓰인 위키피디아의 표현을 빌리자면 생존 분석은 어떠한 event가 발생하기까지에 걸리는 시간 을 추정한다.
다음은 생존 분석의 주요 개념들이다.
-
시간 (time): 상대적인 개념으로의 시간이다. 즉, 분석하려는 대상을 관찰하기 시작한 시점으로부터 경과한 시간이다. A라는 환자가 2022년도 3월에 진단을 받고 같은 해 5월에 event가 일어났다면 t = 2개월이다.
-
사건 (event): 생존의 반대 개념이다. 보통 이쪽에서는 failure라는 표현을 사용한다. 죽음, 사고, 재발 등 생존 분석의 대상이라 할 수 있다. 사건은 한 번만 일어나게 되며 보통 0(일어나지 않음 또는 censored), 1(일어남)으로 표현한다.
-
중도절단 (censored): 생존 분석 데이터의 중요한 특징 중 하나로, 보통 right censored의 특징을 띈다. Right censored는 대상에 아직 사건이 발생하지 않았거나, 기타 다양한 이유(진료를 더이상 나오지 않음, 교통사고로 사망)로 관찰이 종료된 것을 의미한다. 일반적인 regression 분석과의 차이를 만들어주는 데이터의 특징으로 생존 분석을 더 특별하고 까다롭게 만들어주는... 특성이라 할 수 있다.
조금 더 멋진 표현을 사용하자면 다음과 같다.
If only the limit I for the true event time T is known such that T > I, this is called right censoring.
다시 말해, 실제 생존 시간(모름)이 관찰 기간보다 긴 경우 이를 right censored data라고 부른다.
- 생존함수 (survival function): 대상이 특정 시간 t보다 더 오래 생존할 확률을 계산하는 함수이다.
T는 random variable for a person's survival time, t는 specific value for T라 정리해 볼 수 있다.
생존함수는 결국 시간 t 이후에 사건이 발생할 확률을 적분한 것이다. 시작 지점(t=0)에는 모두 살아있으므로 생존함수 값은 1이다. 시간이 지나며 대상의 일부가 사망할 것이기에 생존함수 값은 감소한다.
- 위험함수 (hazard function): 특정 시간 t에 대상에 사건이 발생할 확률이다. 미분한 개념으로 생각하면 편하다. 이 때, t 시점 전까지는 사건이 발생하지 않아야 한다. 쉽게 말해 대상이 t까지 잔존한 상태에서 t시점에 사건이 발생할 확률이다.
Conditional failure rate라 불리고, non-negative, no upper bound 특성을 가지고 있다.
- 누적위험함수 (cumulative hazard function): 위험함수를 0부터 t까지 적분한 값이다. 즉, t시점 전까지 각 순간들마다 사건이 발생할 확률을 모두 더한 값이다.
즉 다음과 생존함수, 위험함수, 누적위험함수는 다음과 같은 관계를 가진다.
설명을 제대로 안했기 때문에 어렵게 느껴질 수 있다. 하지만 이 관계식이 가지는 의미는 결국 "셋 중 하나를 구한다는 것은 나머지 셋을 모두 구한다는 것이나 마찬가지임"이다. 자세한 내용은 Wikipedia - survival analysis를 참고하도록 하자.
생존 분석 방법
지금까지 생존 분석의 기본 개념을 살펴보았다. 이제 right censored data 생김새는 보통 어떻게 생겼고, 어떻게 추정하는지를 자세히 알아보도록 하자.
Data layout
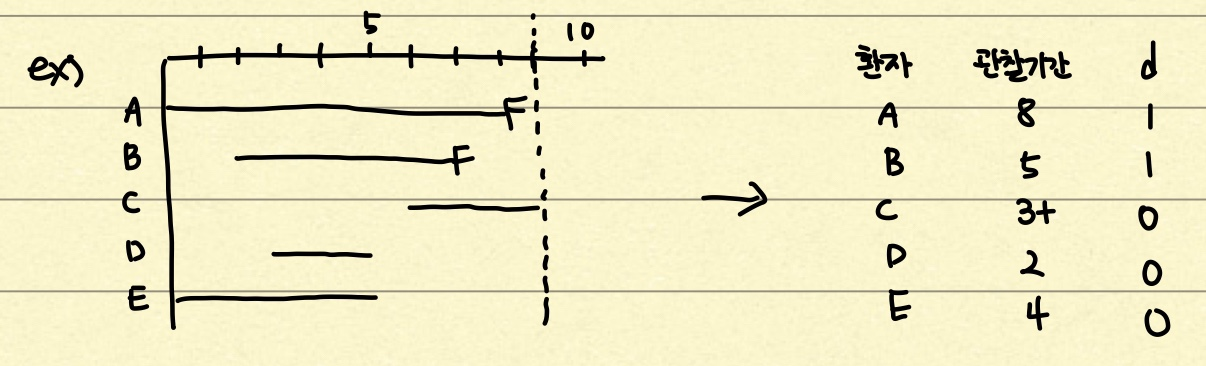
귀찮으니 사진으로 대체하도록 하겠다. 가로축은 시간축, 세로축은 각 환자이다. F라고 쓰여있는 부분은 failure, 즉 사망 등의 event가 일어났다는 뜻이다. A와 B는 관찰 기간 내에 event가 일어났으므로 d=1이라고 표시하는 것이다. C, D, E는 d=0 즉 right censored 환자 데이터이다.
Keplan-Meier Estimation
Kaplan-Meier estimation은 생존 함수(누적 생존률)를 추정하는 가장 단순한 방법이다. 수식은 다음과 같다.
관찰 시간에 따라 사건이 발생한 시점의 사건 발생률을 계산한다! 느낌인데 딱 봤을 때 이해하기가 어려웠다. 바로 그림과 예제를 보면서 알아보도록 하자.
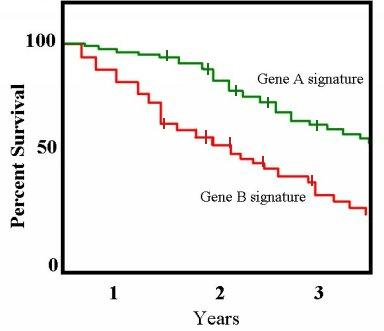
가로축은 time 시간, 세로축은 추정 생존함수 값(확률)을 나타낸다.
추정의 첫번째 단계는 데이터를 시간에 따라 sorting 하는 것이다. 그리고 각 시간마다 생존해 있는 사람 수와 관찰 대상 그룹에 속한 사람 수를 정리해준다. 이 때 관찰 대상 그룹에는 그 시점 t에
- 관찰이 중단된 사람
- 생존해 있는 사람
- 사건이 일어난 사람
이렇게 세가지 부류의 사람이 있는 것이다. 주의할 점은 이 표는 철저하게 "관찰 시간"에 의해 나뉘었다는 점이다. 데이터가 커지면 t=2인 구간에 환자 D 한 명만 이탈한 것이 아니라 여러 명에 대해 변화가 일어날 수 있기 때문이다. 관찰 대상 그룹 관찰이 중단되었거나 사건이 일어난 사람이 존재하는 시점에 한해서 표에 한 줄이 추가되는 것이다.

이렇게 관찰 대상 그룹에 속한 사람 수와 생존자 수를 자세히 설명한 이유는 이게 Kaplan-Meier estimation의 전부이기 때문이다. 이제 계산하면 된다. 누적 생존률을 계산하기 전에 구간 생존률이라는 개념이 등장한다.
누적 생존률은 이를 계속 곱해주면 된다.
그리고 이를 그래프로 나타내어 주면 최종적으로 다음과 같은 그래프를 그릴 수 있다.
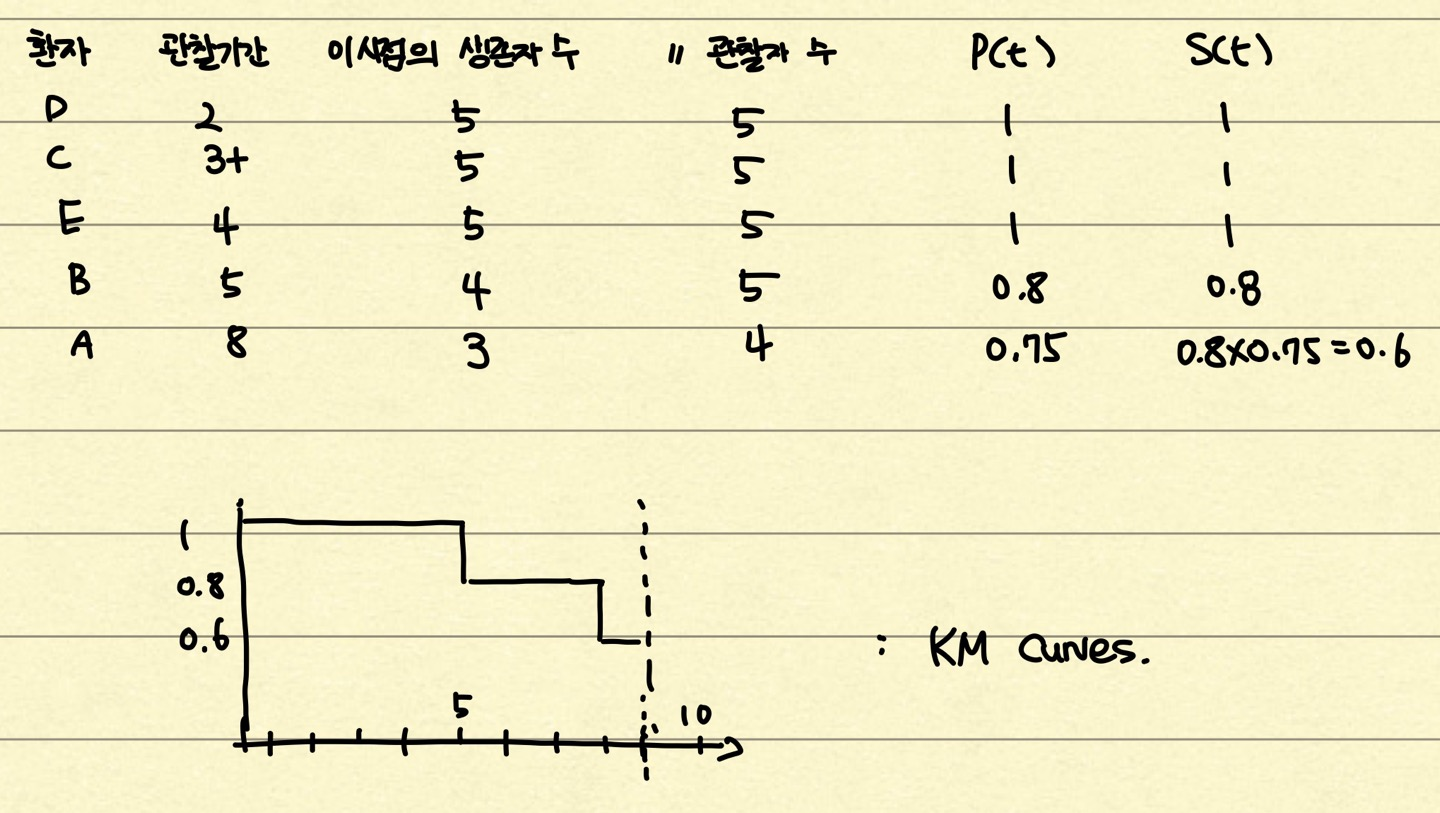
Logrank Tests
지금까지 Keplan-Meier estimation에 대해 알아보았다. Logrank test는 생존 함수 분포를 비교하고 유의한 차이가 있는지 알아보는 가설 검정 기법이다. 예를 들어 신약 A가 환자 집단에게 얼마나 효과적인지 알아보기 위해 신약A를 처방받은 집단과 대조군 집단에 대한 두 curve를 그렸을 때 그 차이를 정량적으로 계산하는 logrank test를 통해 신약A의 유의성을 검증하는 것이다.
여느 significance test와 같이 null hypothesis를 설정하고 이를 얼마나 반증하는지를 계산한다. Null hypothesis는 다음과 같다.
: Two groups come from the same survival distribution
이를 반증하기 위해, 실제 관측값 개수(observed count)와 주어진 가정을 적용했을 때 사건이 일어날 법한 수(expected count)를 각 그룹별 사건 발생 시간의 카이 제곱(chi-square)을 계산하여, 비교하고 결과를 합산하는 방식이다.
비교 대상 그룹이 2개일 때, 카이 제곱 값이 3.841보다 커야 유의미(p-value=0.05)하다고 볼 수 있다. 또한 이 식은 variance를 포함한 log-rank statistics 계산을 근사하는 공식이다. 자세한 내용은 역시 위키피디아를 참고하도록 하자.
Cox Proportional Hazards Model
CoxPHFitter라는 함수는 생존분석 분야에서 가장 보편적으로 쓰이는 함수이다. 1972년에 제안되었음에도 아직까지 여러 연구에서 활발히 사용될 정도로 중요하고 꼭 공부해야하는 개념이다. 이 전에 좀 더 넓은 개념부터 알아보도록 하자.
Survival Prediction 관련 연구는 다음 그림과 같이 크게 네 가지로 나뉜다.
- Non-parametric: 데이터의 feature와 생존 시간 분포 정보를 사용하지 않는 방법이다. 분포 정보를 알 수 없을 때 유용하지만 예측이 부정확 할 수 있습니다. KM estimation이 여기에 속한다.
- Semi-parametric: feature 정보를 활용하지만, 생존 시간 분포 정보를 사용하지 않는 방법입니다. Cox PH 모델이 해당된다.
- Parametric: 생존 시간 분포가 존재한다고 가정하고 회귀 모델로 생존 시간을 예측하는 기법이다. 지수 분포, 베이불(Weibull) 분포, 로지스틱(Logistic) 분포, 정규 분포 등을 사용한다.
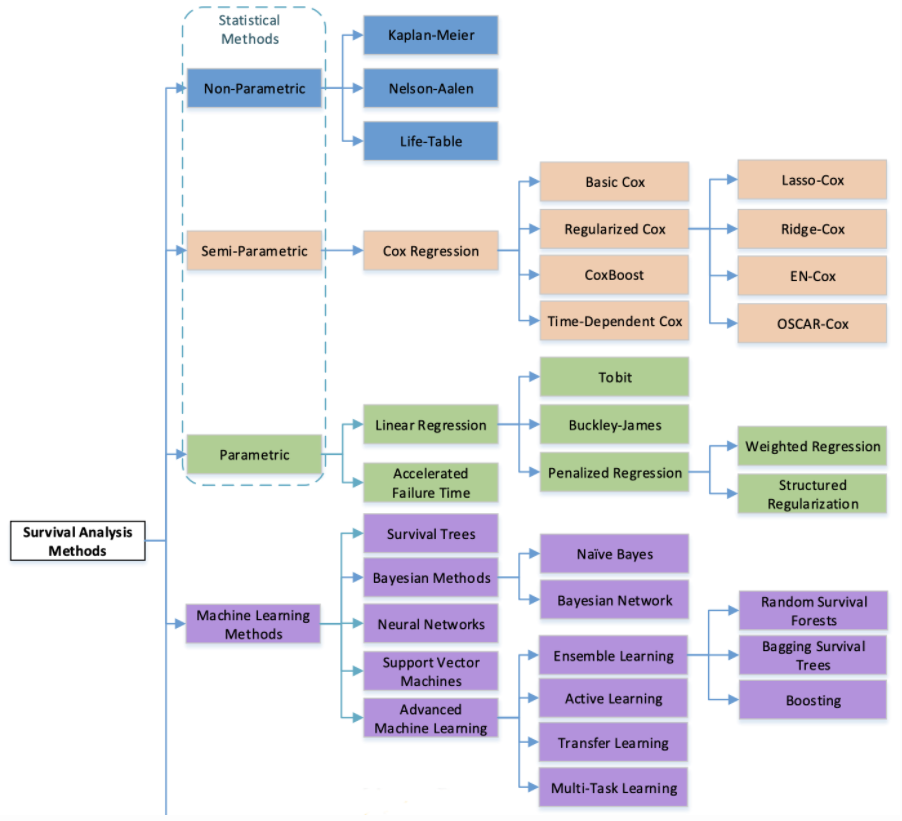
Kaplan-Meier estimation을 짚어 봤을 때, 시간별로 잘라서 사람 수로만 확률을 추정했을 뿐, 환자가 어떤 feature(covariate)를 가지고 있는지 그리고 시간에 지남에 따라 어떻게 정보가 변하는지 등에 대해 고려하지 않았다. Cox Proportional Hazard(Cox PH) 모델은 시간은 여전히 고려하지 않지만, 각 환자의 covariate를 고려하여 생존 함수를 추정하는 방법이다. 그 방법으로, 다음 공식처럼 위험함수(hazard function)를 기저위험(underlying baseline hazard)과 매개변수로 나누어 정의한다.
Exponential function은 위험함수의 non-negative한 성질을 만족하기 위해 쓰인 가정이라 볼 수 있다. (겁먹지 않아도 된다.) 는 시간에 따라 변화하는 baseline hazard function(기저위험함수)이다. 는 흡연여부, 성별 등 대상(환자)의 변수(covariate)이며, 는 모델이 학습해야 하는 계수(coefficient)이다. 공식을 보면 변수와 계수에 시간 가 없다. Cox PH 모델은 변수가 생존에 영향을 주지만 그 영향은 시간과 관계없이 일정하다고 가정한다. 예를 들어 술을 즐겨 마시는 사람은 그렇지 않은 사람보다 사망 위험이 높지만 마신지 얼마 안된 대학생과 계속 마신 중년이나 동일하게 위험하다고 가정한다.
아래 식을 보면 두 대상의 위험 비율(hazard ratio)이 시간 과 시간에 따라 변화하는 기저위험함수 와 독립적이라는 것을 알 수 있다.
위험비(hazard ratio): 변수 한 단위가 변화할 때 변화하는 위험함수 값
이렇게 Cox PH 모델은 위험비가 생존 기간 내내 (시간과 무관하게) 일정하다고 가정하며 이를 비례 위험 가정(proportional hazards assumption) 이라 한다. 이 가정을 등에 업어 기저위험함수를 무시하고 다음과 같은 partial likelihood function을 사용해 계수 를 학습한다.
이 때, partial이라는 수식어가 붙은 이유는 분모가 not complete하기 때문이다. 계산에 포함되는 대상 특징으로는
- failure 되었거나 censored가 이미 된 사람은 포함하지 않는다.
- 이후 censored될 사람이더라도 그 시점에 아직 failure가 일어나지 않았다면 포함한다.
라고 정리할 수 있다. 직관적으로 의 likelihood는 특정 시점에 대상 가 사망했을 때(정답), 그 시점에 관찰 대상 그룹에 속한 모든 사람이 사망할 확률 중 대상 가 사망할 확률을 뜻한다. 이를 아래 식과 같이 log likelihood function으로 바꿔서 사용한다.
DeepSurv
최근 딥러닝의 발전으로 DeepSurv, DeepConvSurv, WSISA 등 neural net을 통해 survival analysis를 수행하는 시도가 많아졌다. 나중에 다시 정리하겠지만 간단히 언급하고 포스팅을 마치도록 하겠다.
Cox PH 모델의 중요 가정 중 하나는 linear proportional hazards condition, 위험함수의 log 값은 대상(환자)의 변수(covariate)와 linear combination라는 가정이다. 이 가정은 다양한 상황을 표현하기에 too simplistic 하기 때문에, 딥러닝을 활용한 nonlinear extension이 DeepSurv 논문에서 시도되었다. 딥러닝에서 모델의 parameter를 학습한다는 것은 결국 하나의 함수를 학습한다는 것으로 해석할 수 있다. DeepSurv의 architecture는 다음과 같다.
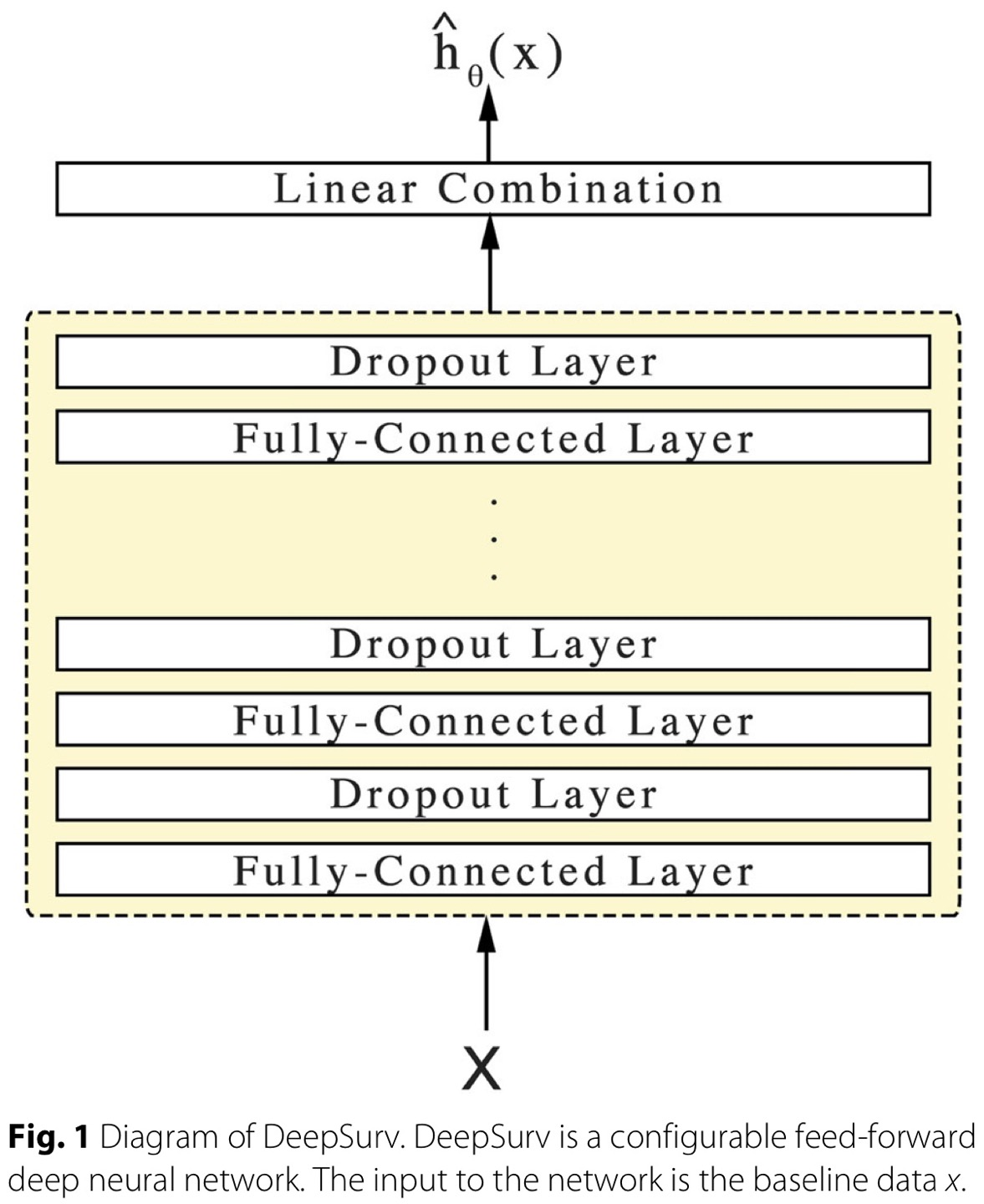
마지막 layer는 latent feature의 linear combination을 수행하는 single node로, log-rist function 의 꼴로 output을 내놓게 된다. 실험적으로도 linear function 뿐만 아니라 non-linear한 function을 잘 학습하였다.
마치며
지금까지 생존분석의 기본 개념과 생존 분석 방법, 그리고 DeepSurv까지 간략하게 알아보았다. 역시 최고의 공부 방법은 남에게 설명하는 것이다. 무심코 지나쳤던 부분을 다시 깊게 생각해볼 수 있었고 잘못된 개념도 바로 잡을 수 있었다.
아직 이해가 안가는 부분은 Cox Loss 부분이다. 지금 다시 찾아보니까 나름의 maximum likelihood estimator로서의 derivation이 나와 있는 것 같은데 이건 나중으로 미루겠다. 아직 likelihood, bounded, unnormalized 등의 개념이랑 친하지 않은 것 같다. 시간 날때마다 계속 친해지려 노력해야 한다!! 아마 다음 생존분석 글은 coxph 모델 이외의 모델이나 surv 내용이 아닐까 싶다.
다음 포스팅은 논문 리뷰가 될 것 같다. 최근에 DeepAttnMISL 논문을 읽었는데 마침 다음 할당된 논문도 attention 관련 논문이다. 고로 다음 포스팅은 attention 관련 논문 리뷰가 될 것이다!! 내일 월요일.. 인데 가서 또 열심히 일해야지 하하 끝까지 읽어주셔서 감사하고, 잘못된 부분이나 궁금한 점 있으면 언제라도 댓글로 남겨주시면 감사하겠습니다. :)
Reference
포스팅을 참고하면서 양심에 찔릴 정도로 hyperconnect tech blog의 글을 많이 참고하였는데 그만큼 잘 정리되어 있으니 이해가 안가는 부분이 있었다면 reference를 타고 방문해 보는 것을 추천한다.
- https://hyperconnect.github.io/2019/07/16/survival-analysis-part1.html
- https://hyperconnect.github.io/2019/08/22/survival-analysis-part2.html
- https://hyperconnect.github.io/2019/10/03/survival-analysis-part3.html
- https://bioinformaticsandme.tistory.com/223
- https://en.wikipedia.org/wiki/Kaplan%E2%80%93Meier_estimator
- https://link.springer.com/book/10.1007/978-1-4757-2555-1
- Katzman, J.L., Shaham, U., Cloninger, A. et al. DeepSurv: personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med Res Methodol 18, 24 (2018). https://doi.org/10.1186/s12874-018-0482-1
