[논문 리뷰] A Survey on Graph Neural Networks for Time Series: Forecasting, Classification, Imputation, and Anomaly Detection

이재호·2025년 2월 22일
논문 리뷰

논문리뷰

목록 보기
3/4

시계열 데이터 관련 연구를 찾아보다 GNN을 활용한 시계열 연구 내용을 정리해 놓은 서베이 논문을 발견하였다. 본 논문은 GNN4TS(GNN을 활용한 시계열 분석) 최신 연구 동향과 모델의 전체적인 구조 및 종류를 잘 설명하고 있다.
https://ieeexplore.ieee.org/document/10636792

Abstract

1. 배경

  • 최근 GNN의 발전으로 시계열 분석에서 GNN 기반 접근법이 증가하고 있다.
  • 기존의 전통적인 방법 및 DNN 기반의 방법이 시간 및 변수 간 관계를 명확히 모델링하는 데 어려움을 겪는 반면, GNN 기반 접근법은 이를 효과적으로 처리할 수 있다.

2. 목표

  • GNN을 활용한 시계열 분석(GNN4TS)의 최신 연구 동향 정리.
  • 시계열 분석을 위한 GNN의 주요 응용 분야를 네 가지로 구분하여 체계적인 분류 제시:
    1. 예측(Forecasting): 시계열 데이터를 기반으로 미래 값을 예측
    2. 분류(Classification): 시계열 패턴을 기반으로 특정 범주에 분류
    3. 이상 탐지(Anomaly Detection): 비정상적 패턴을 탐지하여 이상 징후 감지
    4. 결측값 보완(Imputation): 손실된 데이터를 보완하여 데이터 완전성 향상

3. 내용

  • 대표적인 연구 사례를 소개하고, 주요 연구들이 적용된 산업 및 실제 응용 분야 설명
  • 기존 연구의 한계점을 분석하고, 향후 연구 방향 제안

1. INTRODUCTION

1. 배경 및 필요성

  • 센서 및 데이터 스트리밍 기술의 발전으로 시계열 데이터가 폭발적으로 증가했다.
  • 시계열 데이터 분석은 예측(forecasting), 분류(classification), 이상 탐지(anomaly detection), 결측값 보완(imputation) 등의 다양한 태스크에 활용된다.
  • 전통적인 분석 방법(SVR, GBDT, VAR, ARIMA)들은 비선형성 및 변수 간 복잡한 관계를 제대로 모델링하지 못해 한계가 존재한다.
  • 딥러닝 기술들(CNN, RNN, Transformer)은 성능이 향상되었지만, 비유클리드 공간에서의 Spatial Relations를 명시적으로 모델링하지 못한다.
  • 하지만 Graph Neural Networks(GNNs)은 비유클리드 데이터 표현 학습에 강점을 가지며, 시계열의 공간-시간(Spatial-Temporal) 종속성을 효과적으로 모델링할 수 있다.

2. GNN을 활용한 시계열 분석(GNN4TS)의 연구 발전

  • 초기 연구들은 주로 시계열 예측(forecasting)에 집중되었지만, 최근에는 분류, 이상 탐지, 결측값 보완 등의 다양한 작업에서도 활용되고 있다.
  • 예를 들어, 교통 흐름 예측, 인구 이동 패턴 분석, 기상 예측 등에서 GNN이 효과적으로 사용된다.

3. 기여 내용

  • GNN 기반 시계열 분석(GNN4TS)에 대한 최신 연구를 광범위하게 정리하고 개괄적인 발전 흐름을 제공.
  • 예측, 분류, 이상 탐지, 결측값 보완 등 주요 시계열 분석 작업을 기준으로 연구들을 분류.
  • GNN4TS 모델들이 공간 및 시간 종속성을 어떻게 처리하는지, 전체적인 모델 구조를 기준으로 분류.
  • 단순 개요가 아닌, 세밀한 연구 분류 및 최신 연구 동향을 포함하여 보다 깊이 있는 정보를 제공.
  • 향후 연구자들에게 유용한 오픈 문제 및 연구 방향을 제시.

2. DEFINITION AND NOTATION

  • 시계열 데이터는 일정 기간 동안 수집된 관측값의 연속으로, 정규 샘플링(regularly sampled)과 비정규 샘플링(irregularly sampled, 결측값이 포함될 수 있는 샘플)으로 구분된다.
  • 또한, 시계열 데이터는 단변량(univariate)과 다변량(multivariate)으로 나뉜다.
    • 단변량 시계열: 하나의 변수로 구성된 시계열 데이터
    • 다변량 시계열: 여러 변수(차원)로 구성된 시계열 데이터
  • 논문에서는 다음과 같은 표기법을 사용한다.
    • X: 행렬 (예: 전체 시계열 데이터)
    • x: 벡터 (예: 특정 시간의 데이터)
    • V: 집합 (예: 변수들의 집합)

  1. 단변량 시계열 (Univariate Time Series)

    • 시간에 따라 수집된 단일 스칼라 값의 연속된 관측값.
    • 정규 샘플링: 일정한 시간 간격으로 수집된 경우.
      • 표현: X={x1,x2,…,xT}∈RT,xt∈RX = \{x_1, x_2, \dots, x_T\} \in \mathbb{R}^{T} , x_t \in \mathbb{R}
    • 비정규 샘플링: 시간 간격이 불규칙한 경우.
      • 표현: X={(t1,x1),(t2,x2),…,(tT,xT)}∈RTX = \{(t_1, x_1), (t_2, x_2), \dots, (t_T, x_T)\} \in \mathbb{R}^{T}

  2. 다변량 시계열 (Multivariate Time Series)

    • 시간에 따라 수집된 N차원 벡터의 연속된 관측값.
    • 정규 샘플링: 모든 차원이 동일한 시간 간격으로 수집됨.
      • 표현: X∈RN×T,xt∈RNX \in \mathbb{R}^{N \times T}, x_t \in \mathbb{R}^{N}
    • 비정규 샘플링: 각 차원이 서로 다른 시간 간격에서 수집될 수 있음.
      • 각 시간에서 0개 ~ 최대 NN개 차원의 관측값이 존재 가능.

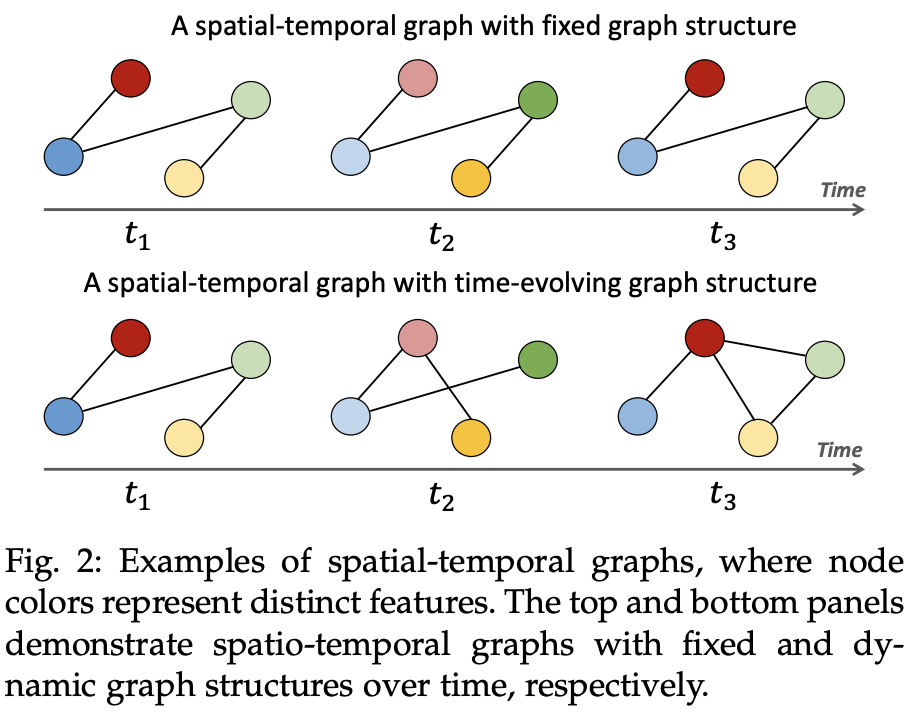
  • 다변량 시계열 데이터는 공간-시간 그래프 (spatial-temporal graph) 형태로 추상화할 수 있어 GNN 연구에서 많이 활용된다.
  • 또한, 두 가지 주요 종속성을 효과적으로 모델링 가능하다.
    1. 시간 간 종속성 (Intertemporal Dependency):
      • 동일한 시계열 내에서 다른 시간 스텝 간의 관계를 의미.
      • 예: 그림 2에서 빨간색 노드의 t1t_1과 t3t_3 간의 변화.
    2. 변수 간 종속성 (Inter-variable Dependency):
      • 다른 시계열 변수들 간의 관계를 의미.
      • 예: 그림 2의 각 시간 스텝에서 4개의 노드 간 공간적 관계의 변화.
  1. 속성 그래프 (Attributed Graph)
  • 각 노드에 속성 집합을 연결한 정적 그래프로, 각 노드의 특성을 나타낸 그래프이다.
  • 수학적으로 G = (A, X)로 정의된다.
    • A: 가중치 인접 행렬(크기: N×NN \times N)로, 각 NN개의 노드 간의 관계를 표현함.
      • 예: AijA_{ij}는 i번 노드와 j번 노드 간의 연결을 나타냄.
    • X: 노드 특성 행렬 (크기: N×DN \times D)로, NN개의 각 노드가 갖는 D차원 특성 벡터를 표현함.
      • 예: xix_i는 i번 노드의 특성 벡터를 의미.

속성 그래프에서의 다차원 엣지 특성

  • 다차원 엣지 특성을 고려할 수도 있으나, 이 논문에서는 스칼라 가중치만을 인접 행렬에 인코딩하여 복잡한 표기를 피했다.
  • 공간-시간 그래프는 속성 그래프들의 연속으로 구성된다. 즉, 공간-시간 그래프는 여러 개의 속성 그래프들이 시간에 따라 변하는 형태로 연결된다.
  • 이를 통해 다변량 시계열 데이터를 시간에 따라 변화하는 혹은 고정된 구조적 정보와 결합하여 표현한다. (예: 센서가 일정한 위치에서 데이터를 수집하고 있으면 그 위치는 고정된 구조적 정보가 될 수 있다. 반면, 센서의 위치가 이동하거나 변화하면 구조적 정보도 변할 수 있다.)
  1. 공간-시간 그래프 (Spatial-temporal Graph)
  • 이산 시간 동적 그래프(discrete-time dynamic graph)로 해석될 수 있다.
  • 시간 t에서의 속성 그래프는 Gt=(At,Xt)G_t = (A_t, X_t)로 표현된다.
    • At∈RN×NA_t \in \mathbb{R}^{N \times N}: 시간 t에서의 인접 행렬
    • Xt∈RN×DX_t \in \mathbb{R}^{N \times D}: 시간 t에서의 특징 행렬
  • 인접 행렬 AtA_t는 시간이 지나면서 변할 수도 있고, 고정될 수도 있다.
  • 시계열 데이터를 추상화할 때, Xt:=xt∈RNX_t := x_t \in \mathbb{R}^N으로 표현된다.
  • GNN의 주요 연산 중 하나는 이웃 노드 간 정보를 교환하는 Graph Convoluntion이다.
  • 시계열 분석에서는 이 연산을 통해 그래프 엣지로 표현된 변수 간 의존성을 명시적으로 반영할 수 있다.
  • GNN은 공간적 차원에서 입력 신호를 학습 가능한 함수로 변환하여 이 작업을 수행한다.
  1. 그래프 신경망 (Graph Neural Network, GNN)
    • 속성 그래프 G=(A,X)G = (A, X) 에서,
      노드 viv_i 의 DD-차원 특징 벡터 xix_i는 xi=X[i,:]∈RDx_i = X[i, :] \in \mathbb{R}^D 로 정의한다.
    • 주요 함수:
      • AGGREGATE(·): 이웃 노드들로부터 메시지를 계산하고 집계.
      • COMBINE(·): 집계된 메시지와 이전 상태를 결합하여 노드 임베딩을 변환.
    • k번째 레이어에서의 연산:
      • ai(k)=AGGREGATE(k)({hj(k−1):vj∈N(vi)})a_i^{(k)} = AGGREGATE(k)\left(\{h_j^{(k-1)} : v_j \in N(v_i)\}\right)
      • hi(k)=COMBINE(k)(hi(k−1),ai(k))h_i^{(k)} = COMBINE(k)\left(h_i^{(k-1)}, a_i^{(k)}\right)
      • ai(k)a_i^{(k)} : kk번째 레이어에서 이웃 노드들로부터 집계된 메시지
      • hi(k)h_i^{(k)} : kk번째 레이어에서 노드 viv_i를 임베딩한 노드
    • 입력/출력:
      • 입력: hi(0):=xih_i^{(0)} := x_i
      • 출력: hi(K):=hih_i^{(K)} := h_i
  • 위처럼 spatial GNNs는 그래프 상에서 노드들 간의 정보 교환을 직접적으로 정의하는 반면, spectral GNNs는 스펙트럴 그래프 이론을 기반으로 합성곱을 정의한다.
  • 모든 시계열 데이터는 그래프 구조를 갖고 있지 않다.
  • 따라서, 그래프 구조를 생성하기 위한 전략으로 휴리스틱 방법과 데이터로부터 학습 전략이 있다.

휴리스틱 기반 그래프 (Heuristic-based Graphs)
이 방법은 데이터에서 휴리스틱을 사용하여 그래프 구조를 얻는 방법으로, 주요 접근법은 다음과 같다.

  1. Spatial Proximity: 노드 간의 지리적 위치를 기준으로 그래프 구조를 정의한다. 예를 들어, 시간 시계열 데이터가 지리적 특성을 갖는 경우, 최단 이동 거리 기반으로 인접 행렬을 구성한다
    • Ai,j=1dijA_{i,j} = \frac{1}{d_{ij}} (단, dij≠0d_{ij} \neq 0)
  2. Pairwise Connectivity: 노드 간의 연결성을 기준으로 그래프 구조를 정의한다. 예를 들어, 교통망에서처럼 두 노드가 직접 연결된 경우 인접 행렬을 설정한다.
    • Ai,j=1A_{i,j} = 1 (직접 연결된 경우), Ai,j=0A_{i,j} = 0 (그렇지 않은 경우)
  3. Pairwise Similarity: 유사한 속성을 가진 노드를 연결하여 그래프를 구성한다. 예를 들어, 시계열 데이터 간 코사인 유사도를 기반으로 인접 행렬을 구성할 수 있다.
    • Ai,j=xiTxj∥xi∥∥xj∥A_{i,j} = \frac{x_i^T x_j}{\|x_i\| \|x_j\|} (코사인 유사도, ∥∥\|\|는 유클리드 norm을 의미.)
  4. Functional Dependence: 노드 간의 알려진 기능적 의존성을 기준으로 그래프 구조를 정의한다. 예를 들어, Granger causality(인과 관계 분석) 등을 사용하여 인접 행렬을 구성할 수 있다.
    • Ai,j=1A_{i,j} = 1 (노드 jj가 노드 ii를 그랜저 인과할 때(영향을 줄 때)), Ai,j=0A_{i,j} = 0 (그렇지 않은 경우)

학습 기반 그래프 (Learning-based Graphs)
이 방법은 데이터를 기반으로 그래프 구조를 학습하는 방법을 의미한다. 이 방법은 end-to-end 방식으로 그래프 구조를 학습하며, 이를 통해 주어진 다운스트림 작업을 해결하는 데 최적화된 그래프를 생성한다. 주요 내용은 다음과 같다.

  • 그래프 정의: 그래프 A는 학습 가능한 모델 파라미터 ΘΘ와 시계열 데이터 XX를 바탕으로 함수 ρ(·)로 정의된다. 즉, A=ρ(Θ,X)A = \rho(\Theta, X)와 같이 모델 파라미터와 시계열 데이터를 이용해 그래프 구조를 학습한다.
  • Embedding 기법: 노드의 임베딩 벡터를 비교하여 각 엣지의 존재를 정의한다.
    • 예: Ai,j=ReLU(ΘiTΘj)A_{i,j} = \text{ReLU}(\Theta_i^T \Theta_j), ΘΘ는 각 노드 ii, jj의 임베딩 벡터.
  • Attention 기법: 노드 신호 간의 attention scores를 계산하여 그래프 A를 정의한다.
  • Sparsification (희소화 기법): ReLU activation나 top-k selection과 같은 기법을 사용해, 낮은 가중치 또는 null 값을 가진 엣지를 제거하여 계산 부하를 줄인다.
  • 확률적 모델링: 그래프 A를 이산 확률 변수로 모델링하고, 그 분포를 학습한다.
    • 예를 들어, pΘ(A∣X)p_{\Theta}(A | X)처럼 분포를 학습하면서 모델 파라미터와 함께 그래프를 정의할 수 있다.

3. FRAMEWORK AND CATEGORIZATION

  • 3.1: 시계열 분석을 위한 GNNs의 포괄적인 태스크 기반 분류 체계 (task-oriented taxnomy for GNNs) 제시.
  • 3.2: GNN 아키텍처를 위한 통합방법론적 프레임워크 소개 및 다중 태스크에서의 시계열 데이터 인코딩 방법 소개.
    + 모듈 소개. 모든 GNN 아키텍처는 다음 두 가지 주요 모듈로 구성된다:
    1. 그래프 기반 처리 모듈 fθf_{\theta}: 그래프 데이터를 처리하는 공통 모듈.
    2. 다운스트림 작업에 특화된 모듈 pϕp_{\phi}: 특정 시계열 분석 작업을 수행하는 모듈 .

3.1 Task-oriented Taxonomy

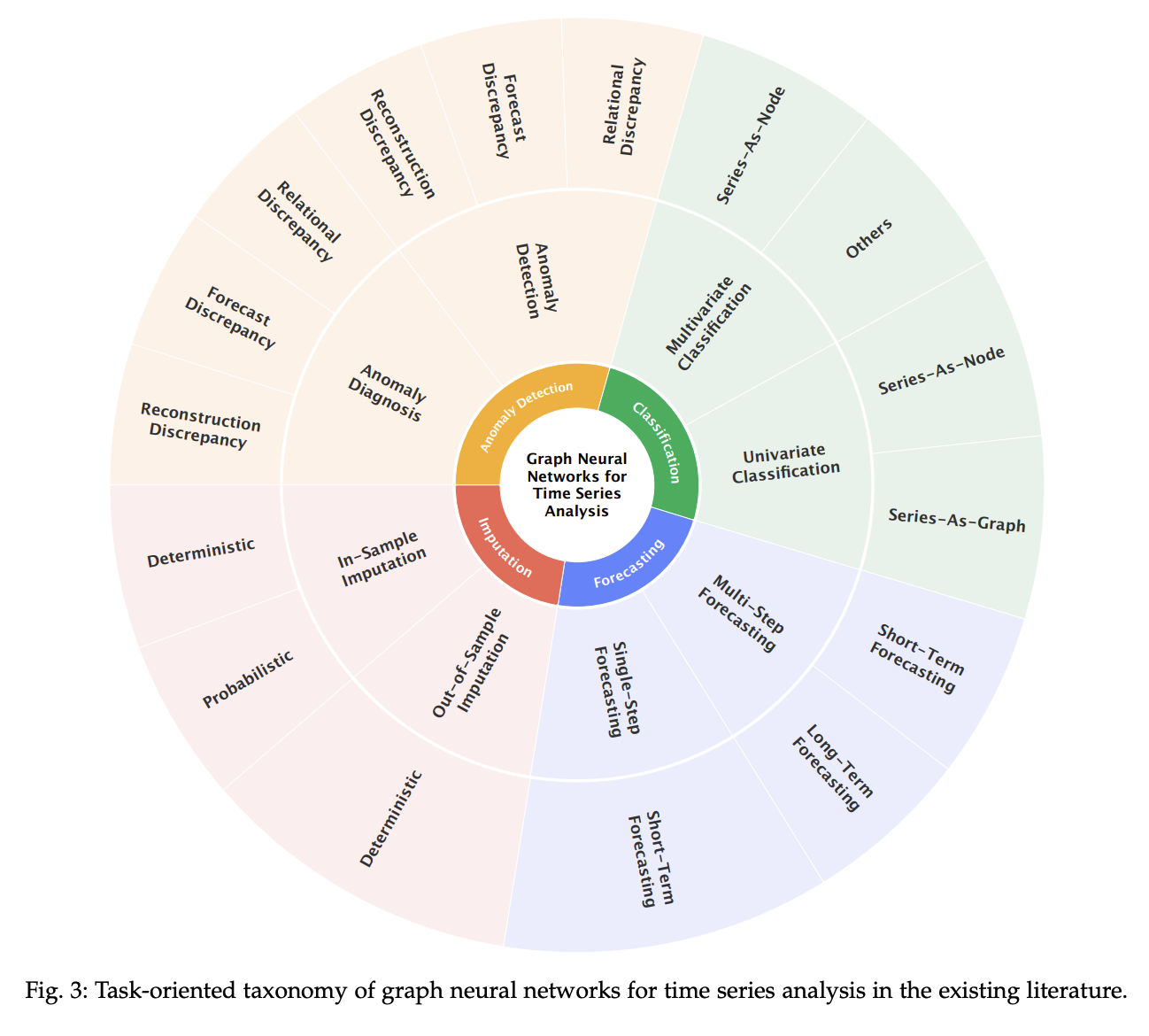
  • 본 논문에서는 태스크를 크게 forecasting(예측), anomaly detection(이상 탐지), imputation(결측값 보완), classification(분류) 로 카테고리를 나눴다.
  • 위와 같은 태스크들은 spatial-temporal graph neural networks (STGNNs) 모델 기반으로 수행된다.

1. Time Series Forecasting

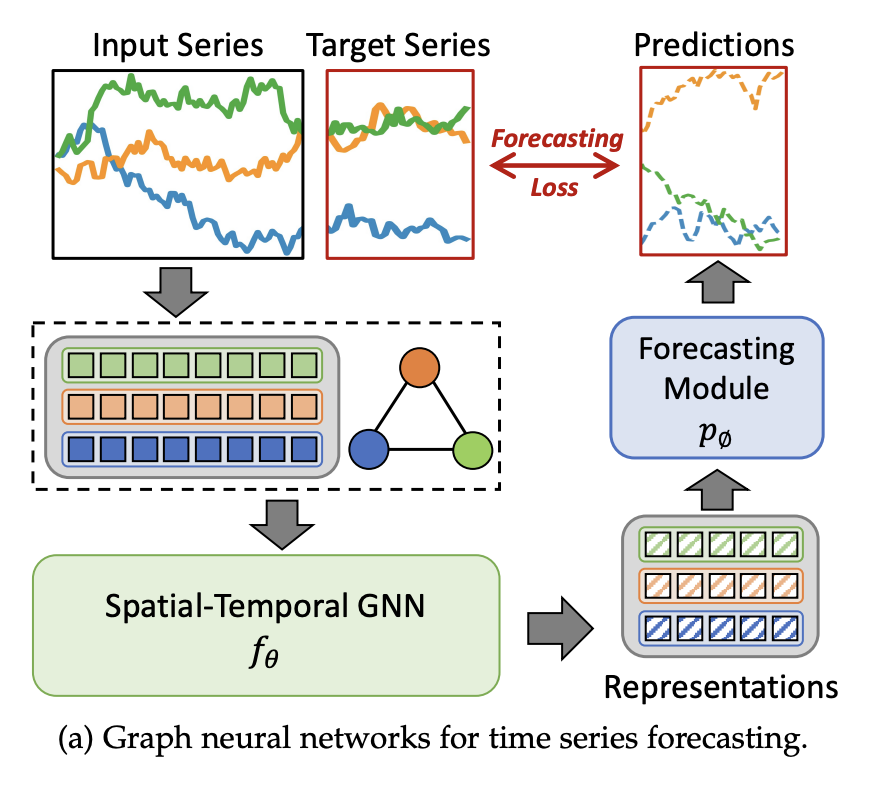
시계열 예측은 과거의 시계열 데이터를 기반으로 미래 값을 예측하는 것이다. 위 그림 4a에서 시계열 예측에 대한 모델 구조를 알 수 있다.

1. 시계열 예측의 두 가지 유형
시계열 예측은 적용 목적에 따라 두 가지 유형으로 나뉜다.

  1. 단일 스텝 예측 (Single-step-ahead forecasting)
    • 한 번에 하나의 미래 값을 예측하는 방식.
    • 예를 들어, 현재 시점 tt 에서 HH 만큼 떨어진 미래값만 예측할 경우, 목표값 YY 는 Y:=Xt+HY := X_{t+H} 가 된다.
  2. 다중 스텝 예측 (Multi-step-ahead forecasting)
    • 한 번에 일정한 시간 구간에 대한 미래 값을 예측하는 방식.
    • 예를 들어, Y:=Xt+1:t+HY := X_{t+1:t+H} 처럼 연속적인 HH 개의 미래값을 예측한다.

2. 예측 모델의 최적화 방식

  • 예측 모델은 STGNN (Spatial-Temporal GNN) fθ(⋅)f_{\theta}(\cdot) 과 predictor pϕ(⋅)p_{\phi}(\cdot) 로 구성된다.
  • 이 모델은 다음의 최적화 방법을 통해 학습된다.
θ∗,ϕ∗=arg⁡min⁡θ,ϕLF(pϕ(fθ(Xt−T:t,At−T:t)),Y)(6)\theta^*, \phi^* = \arg \min_{\theta, \phi} L_F \left( p_{\phi} \left( f_{\theta}(X_{t-T:t}, A_{t-T:t}) \right), Y \right) \tag{6}
  • 용어 의미는 다음과 같다.
    • fθ(⋅)f_{\theta}(\cdot) : GNN 모델 (STGNN)
    • pϕ(⋅)p_{\phi}(\cdot) : predictor (일반적으로 다층 퍼셉트론, MLP)
    • Xt−T:t,At−T:tX_{t-T:t}, A_{t-T:t} : 시간 및 공간 그래프. G={Gt−T,Gt−T+1,...,Gt}G = \{G_{t-T}, G_{t-T+1}, ..., G_t\}
    • LF(⋅)L_F(\cdot) : 예측 손실 함수 (일반적으로 MSE 또는 MAE)

만약 기본적인 그래프 구조가 고정되어 있다면, 단순히 공간 정보를 나타내는 AA를 At:=AA_t := A 로 설정할 수도 있다.

3. 예측 방법의 종류

  1. 결정론적 예측 (Deterministic Forecasting)

    • 대부분의 기존 연구는 예측값과 실제값 간의 오차를 최소화하는 방식 (Equation 6)을 사용한다.
    • 예: STGCN (Spatio-Temporal Graph Convolutional Network) [54], MTGNN (Multi-Scale Temporal Graph Neural Network) [51]

  2. 확률적 예측 (Probabilistic Forecasting)

    • 예측을 확률적으로 수행하는 방법으로, 오차 최소화가 직접적으로 최적화되지는 않지만 같은 목적을 갖는다.
    • 예: DiffSTG [55]

4. 예측 범위에 따른 분류

  • 단기 예측 (Short-term forecasting) : 예측 시계열 길이 HH 가 짧은 경우
  • 장기 예측 (Long-term forecasting) : 예측 시계열 길이 HH 가 긴 경우

결론적으로, 시계열 예측은 과거 데이터를 바탕으로 미래 값을 예측하는 작업이며, 단일 스텝 예측과 다중 스텝 예측으로 나뉘며, STGNN과 predictor(다중퍼셉트론)를 활용해 최적화한다.

2. Time Series Anomaly Detection

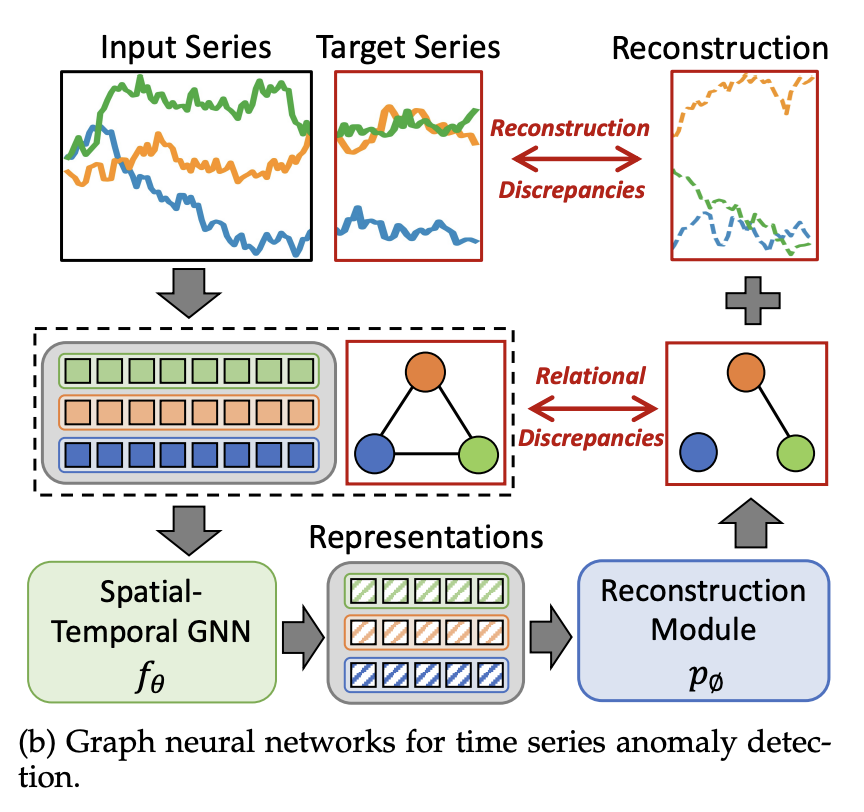
시계열 이상 탐지는 시계열 데이터에서 비정상적인 패턴이나 예기치 않은 이벤트를 탐지하는 것이다. 그림 4b에서 시계열 이상 탐지에 대한 모델 구조를 볼 수 있다.

1. 이상 탐지의 주요 유형

  • 이상 탐지 (Anomaly Detection): 언제 이상 현상이 발생했는지를 찾아내는 것.
  • 이상 진단 (Anomaly Diagnosis): 이상이 발생한 원인과 그 이유를 분석하는 것.

이상 탐지는 일반적으로 비지도 학습 (Unsupervised Learning) 문제로 다루어지며, 정상적인 데이터 패턴을 학습한 후, 이상값이 발생하면 높은 점수를 출력하는 방식으로 탐지를 수행한다.

2. 이상 탐지 모델의 학습 과정

  • 이상 탐지 모델의 학습은 예측 최적화 과정(Equation 6)과 유사하게 진행된다.
  • 모델은 STGNN fθ(⋅)f_{\theta}(\cdot) 와 predictor pϕ(⋅)p_{\phi}(\cdot) 로 구성된다.
  • 일반적으로 모델은 정상적인 데이터만을 학습하며, 예측 기반(Forecasting) 방법과 재구성 기반(Reconstruction) 방법을 활용한다.
  1. 예측 기반 학습 (Forecasting-based Training)
    • 정상적인 과거 데이터를 입력으로 받아 미래 값을 예측하는 방식.
    • 정상적인 데이터에 대해 예측 오차가 낮아지도록 학습됨.
  2. 재구성 기반 학습 (Reconstruction-based Training)
    • 정상적인 데이터 패턴을 학습하여, 입력 데이터를 그대로 복원하도록 학습.
    • 정상적인 데이터일수록 원본과 재구성된 데이터 간의 차이가 작아지도록 최적화됨.

3. 이상 탐지의 원리

  • 모델은 정상 데이터만을 학습하기 때문에, 비정상적인 입력(이상 데이터)을 받으면 예측 오차(또는 재구성 오차)가 커지게 된다.
  • 즉, 이상값이 포함된 데이터를 입력하면 모델이 정상적인 패턴을 따르지 못하여 평소보다 큰 오차(discrepancy)를 출력하게 된다.
  • 이 차이를 감지하여 이상 탐지를 한다.

4. 이상 탐지의 임계값 설정

  • 이상 탐지에서 이상값과 정상값을 구분하는 기준(Threshold)은 중요한 하이퍼파라미터이다.
  • 이상값은 드문 사건(Rarity of anomalies)이므로, 거짓 경보(false alarm) 비율을 고려하여 적절한 임계값을 설정해야 한다.

5. 이상 원인 분석 (Anomaly Diagnosis)

  • 이상 원인을 분석하기 위해 각 노드(Channel Node)의 오차를 계산하고 이를 하나의 이상 점수(Anomaly Score)로 통합하는 전략이 사용된다.
  • 이를 통해 어떤 변수(채널)가 이상 사건에 기여했는지 분석이 가능하다.

요약

  • 이상 탐지는 비정상적인 이벤트를 감지하는 작업 .
  • 비지도 학습(Unsupervised Learning) 방식으로 정상 데이터 패턴을 학습.
  • 이상값이 포함되면 모델이 정상적인 패턴을 따르지 못해 예측 오차가 증가 → 이를 통해 이상 감지.
  • 임계값(Threshold) 설정이 중요하며, 거짓 경보 비율을 고려해야 함.
  • 각 노드의 기여도를 분석하여 이상 발생 원인 파악 가능.

3. Time Series Imputation

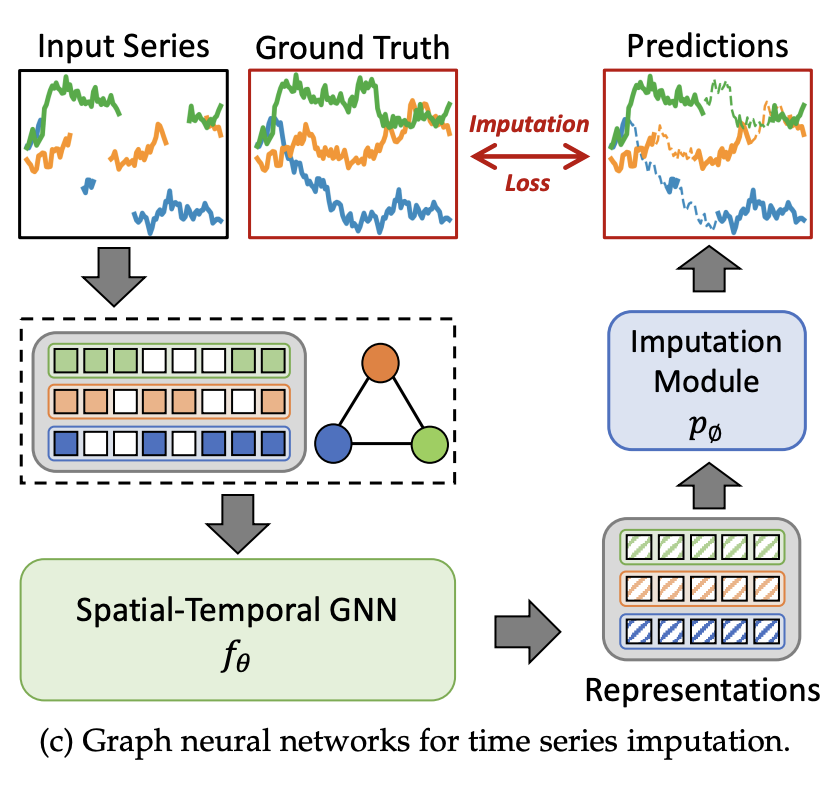
시계열 결측값 보완은 시계열 데이터에서 누락되거나 불완전한 값을 추정하고 채우는 것이다. 그림 4c에서 모델의 구조를 볼 수 있다.

1. Imputation 종류

  1. In-Sample Imputation
    • 주어진 시계열 데이터 내에서 누락된 값을 채우는 방법.
    • 예를 들어, 특정 시간 구간에서 일부 값이 빠진 경우 해당 부분을 추정하여 보완.
  2. Out-of-Sample Imputation
    • 모델이 학습 데이터에 포함되지 않은 새로운 데이터의 누락된 값을 추정하는 방법.
    • 예를 들어, 과거 데이터를 이용해 미래 데이터를 보간(보완)하는 방식.

2. 최적화 방식

보간의 최적화 수식은 다음과 같다.

θ∗,ϕ∗=arg⁡min⁡θ,ϕLI(pϕ(fθ(X~t−T:t,At−T:t)),Xt−T:t)\theta^*, \phi^* = \arg\min_{\theta, \phi} L_I \left( p_{\phi}( f_{\theta} (\tilde{X}_{t-T:t}, A_{t-T:t})), X_{t-T:t} \right)

여기서, 용어의 의미는 다음과 같다.

  • fθ(⋅)f_{\theta}(\cdot) : GNN 모델 (STGNN)
  • pϕ(⋅)p_{\phi}(\cdot) : 보완(추정) 모듈 (ex. 다층 퍼셉트론, MLP)
  • X~t−T:t\tilde{X}_{t-T:t} : 일부 값이 누락된 입력 데이터 (보간이 필요한 데이터)
  • Xt−T:tX_{t-T:t} : 완전한 데이터 (정답 데이터)
  • At−T:tA_{t-T:t} : 시간에 따른 그래프 구조 정보
  • LI(⋅)L_I(\cdot) : 보간 손실 함수 (MSE, MAE 등)

3. 보간 방식별 모델 학습과 평가 방법

  1. In-Sample Imputation
    • 모델이 누락된 값을 포함한 데이터 X~\tilde{X} 를 입력으로 받아 실제 정답 데이터 XX 와 비교하여 손실을 줄이도록 학습.
    • 학습 및 평가 모두 같은 데이터 구간에서 수행
  2. Out-of-Sample Imputation
    • 모델이 과거 데이터 X~t−T:t\tilde{X}_{t-T:t} 로부터 학습하고, 미래 데이터 Xt:t+HX_{t:t+H} 의 누락된 값을 예측하도록 평가.
    • 학습 및 평가 데이터가 서로 다른 시간 범위에 존재.

4. Probabilistic Imputation vs Deterministic Imputation

보간 과정도 예측이나 이상 탐지와 마찬가지로 결정적(Deterministic) 또는 확률적(Probabilistic) 방식으로 수행될 수 있다.

  • 결정적 보간 (Deterministic Imputation)
    • 한 가지 정답을 예측하는 방식.
    • 예) GRIN 모델은 누락된 값을 직접 채움.
  • 확률적 보간 (Probabilistic Imputation)
    • 데이터의 분포를 학습하여 가능한 값을 확률적으로 예측.
    • 예) PriSTI 모델은 분포 기반으로 보간.

요약

  • Time Series Imputation은 누락된 데이터를 채우는 작업으로, 샘플 내(in-sample)와 샘플 외(out-of-sample) 방식이 존재한다.
  • 학습 목표는 STGNN과 보간 모듈을 학습하여 손실을 최소화하는 것이다.
  • 방식은 결정적(Deterministic) 또는 확률적(Probabilistic) 방법으로 나뉜다.
  • 손실은 예측값과 실제값의 차이(MAE, MSE) 를 줄이는 방향으로 최적화한다.

4. Time Series Classification

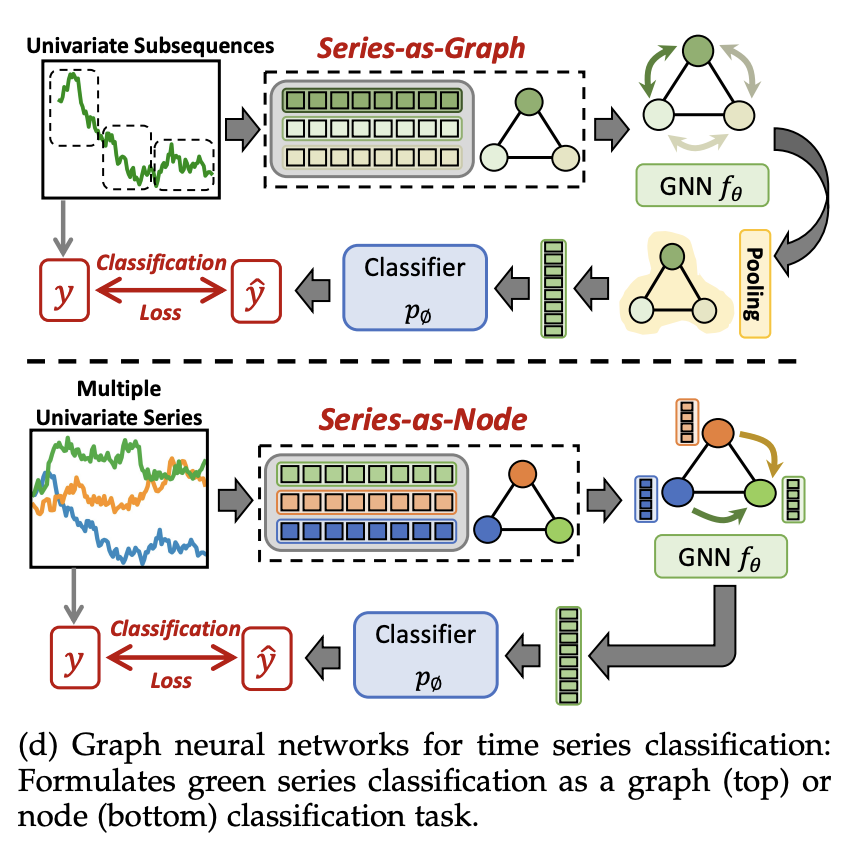
시계열 분류는 주어진 시계열 데이터의 패턴을 분석하여 적절한 label을 할당하는 것이다.
단순히 데이터 내 패턴을 찾는 것이 아니라, 클래스(label)별 차별적인 특징을 발견하는 것이 핵심이다. 모델의 구조는 그림 4b와 같다.

1. 최적화 방식
시계열 분류의 최적화 수식은 다음과 같이 정의된다.

θ∗,ϕ∗=arg⁡min⁡θ,ϕLC(pϕ(fθ(X,A)),Y)\theta^*, \phi^* = \arg\min_{\theta, \phi} L_C \left( p_{\phi}( f_{\theta}(X, A)), Y \right)

용어의 의미는 다음과 같다.

  • fθ(⋅)f_{\theta}(\cdot) : GNN (패턴을 추출하는 역할)
  • pϕ(⋅)p_{\phi}(\cdot) : Classifier (클래스를 예측하는 역할)
  • XX : 입력 시계열 데이터
  • AA : 시계열 간 관계를 표현하는 인접 행렬 (Adjacency Matrix)
  • YY : 정답(Label), 원-핫 벡터 형태
  • LC(⋅)L_C(\cdot) : 분류 손실 함수 (Cross-Entropy 등)

2. 시계열 분류 방식

시계열 분류에는 그래프 분류 (Series-as-Graph)와 노드 분류 (Series-as-Node)의 두 가지 분류 방식이 있다.

1. 그래프 분류 (Series-as-Graph)

  • 각 시계열을 그래프로 변환하여 분류하는 방식.
  • 시계열 데이터를 작은 서브시퀀스(subsequence) 로 분할하고, 이를 그래프의 노드로 취급한다.
  • 그래프의 구조
    • 노드: 시계열의 서브시퀀스 X∈RN×WX \in \mathbb{R}^{N \times W} (W: window size)
    • 엣지(Edge): 서브시퀀스 간 관계를 나타내는 인접 행렬 AA
  • GNN 모델(fθ(⋅)f_{\theta}(\cdot))이 그래프 컨볼루션과 풀링을 수행하여 그래프 특징을 압축한다.
  • Classifier(pϕ(⋅)p_{\phi}(\cdot))가 해당 특징을 기반으로 그래프의 label을 예측한다.

2. 노드 분류 (Series-as-Node)

  • 각 시계열을 하나의 노드로 간주하는 방식.
  • 여러 개의 시계열을 포함하는 데이터셋을 그래프로 모델링.
  • 그래프의 구조
    • 노드: 각 시계열 데이터 X∈RN×TX \in \mathbb{R}^{N \times T}
    • 엣지: 시계열 간 관계를 나타내는 인접 행렬 AA
  • GNN 모델(fθ(⋅)f_{\theta}(\cdot))이 시계열 간 관계를 활용하여 노드의 특징을 추출한다.
  • Classifier(pϕ(⋅)p_{\phi}(\cdot))가 해당 특징을 기반으로 노드(시계열)마다 클래스(label)를 할당한다.

요약

  • 시계열 분류는 각 시계열 데이터가 어떤 클래스(label)에 속하는지 예측하는 작업이다.
  • Series-as-Graph: 하나의 시계열을 여러 개의 서브시퀀스로 분할하여 그래프로 모델링하는 방법.
  • Series-as-Node: 각 시계열을 하나의 노드로 취급하여 시계열 간 관계를 학습하는 방법.
  • GNN을 활용하면 시계열의 패턴뿐만 아니라 서로 다른 시계열 간의 관계도 고려할 수 있다.
  • 최종적으로 one-hot 벡터 YY 형태로 라벨을 예측하여 분류를 수행한다.

3.2 Unified Methodological Framework

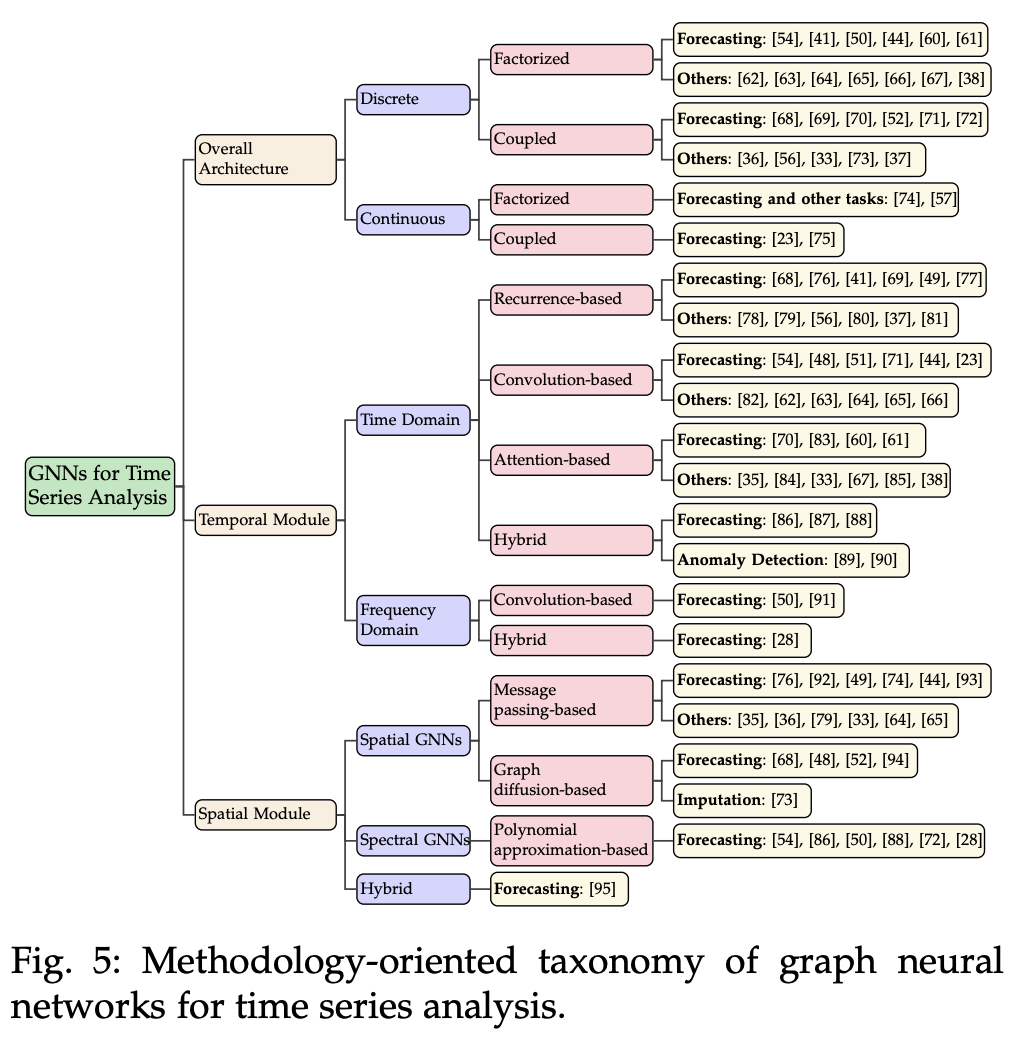
그림 5에서는 STGNN(Spatial-Temporal Graph Neural Networks, 시공간 그래프 신경망)을 활용한 시계열 분석을 위한 통합 방법론적 프레임워크를 제시한다. 이 프레임워크는 기존 연구에서 다양한 다운스트림 태스크(Fig. 3)에 사용되는 시계열 데이터를 인코딩하는 기본 구조로 작용한다.

STGNN은 공간적 정보와 시간적 정보를 모두 반영하는 특징을 갖는다:

  • 공간 정보 (Spatial Information): 그래프에서 노드 간의 관계를 고려하여 공간적 특성을 학습함.
  • 시간 정보 (Temporal Information): 노드 속성이 시간에 따라 어떻게 변화하는지를 반영함.

STGNN을 세 가지 관점에서 체계적으로 분류한다:

  • 공간 모듈 (Spatial Module): 공간적 관계를 모델링하는 방식
  • 시간 모듈 (Temporal Module): 시계열 데이터를 처리하는 방식
  • 전체 모델 아키텍처 (Overall Architecture): 모델의 전반적인 구조

1. Spatial Module

시계열 데이터 간의 의존성(Dependency)을 모델링하기 위해 STGNN은 정적 그래프(Static Graph)에서 사용되는 GNN의 설계 원칙을 따른다.

이러한 공간적 모델링 기법은 크게 세 가지 유형으로 분류할 수 있다:

  1. 스펙트럼 기반 GNN (Spectral GNNs)
    • 그래프 스펙트럼 이론(Spectral Graph Theory)을 기반으로 동작.
    • 그래프 쉬프트 연산자(Graph Shift Operator), 즉 그래프 라플라시안(Graph Laplacian)을 활용하여 그래프의 frequency domain에서 노드 간 관계를 학습.
  2. 공간 기반 GNN (Spatial GNNs)
    • 스펙트럼 GNN보다 단순한 방식으로 각 노드의 이웃(neighborhood)을 중심으로 필터를 직접 설계하여 노드 관계를 학습.
    • 두 가지 주요 접근 방식
      • 그래프 확산 기반(Graph Diffusion-based)
      • 메시지 전달 기반(Message Passing-based)
    • Graph Transformers[100]는 메시지 전달 신경망(Message Passing Neural Networks, MPNN)[101]의 확장 형태로, 공간 GNN의 기능을 더욱 확장시킨다.
  3. 하이브리드 GNN (Hybrid Approaches)
    • 스펙트럼 및 공간 기반 방법론을 결합하여 각 방식의 장점을 극대화하는 기법.

즉, STGNN에서 공간 모듈(Spatial Module)은 노드 간 관계를 학습하는 방법을 다루며, 이를 위해 Spectral, Spatial, Hybrid 방식으로 접근할 수 있다

2. Temporal Module

STGNN(시공간 그래프 신경망)은 시계열 데이터에서 시간적 의존성(Temporal Dependency)을 학습하기 위해, 공간 모듈(Spatial Module)과 함께 동작하는 시간 모듈(Temporal Module)을 포함한다.

시간적 패턴을 모델링하는 방법은 크게 두 가지 방식으로 나뉜다:

1. 시간 도메인(Time Domain)에서의 접근 방식
이 방식에서는 Temporal Dependency을 직접 학습하며, 주요 기법은 다음과 같다.

  • 순환 신경망 기반 (Recurrence-based)
    • RNN(순환 신경망, Recurrent Neural Networks)과 같은 모델을 활용하여 시계열 데이터를 순차적으로 처리.
    • 대표적인 모델: RNN, LSTM, GRU
  • 합성곱 기반 (Convolution-based)
    • TCN(Temporal Convolutional Networks, 시계열 합성곱 네트워크) 등을 활용하여 고정된 크기의 필터로 시계열 데이터를 학습.
    • CNN을 확장하여 장기 의존성(Long-term Dependency)도 학습 가능.
  • 어텐션 기반 (Attention-based)
    • Transformer 모델을 사용하여 가중치를 학습하고, 시간적 패턴을 동적으로 반영.
  • 하이브리드 방식 (Hybrid)
    • 위의 기법들을 조합하여 더 강력한 성능을 내는 방식.

2. Frequency Domain에서의 접근 방식

  • 시계열 데이터를 frequency 영역에서 해석하는 기법.
  • 정확한 시간 순서보다는 패턴과 트렌드를 학습하는 데 유리.
  • 대표적인 방법: 푸리에 변환(Fourier Transform)을 활용한 직교 공간 투영(Orthogonal Space Projections).

요약

  • STGNN은 시간적 패턴을 모델링하기 위해 시간 모듈을 포함한다.
  • 시간 도메인에서는 RNN, TCN, Transformer 등을 활용한다.
  • frequency 도메인에서는 푸리에 변환 등의 기법을 사용하여 시계열 데이터를 분석한다.

3. Model Architecture

STGNN에서 공간 모듈(Spatial Module)과 시간 모듈(Temporal Module)을 통합하는 방식에는 이산적(Discrete) 또는 연속적(Continuous) 방식이 있다.
그리고 다음과 같은 하위 구조로 구분된다: 분리형(Factorized) 구조와 결합형(Coupled) 구조

1. 분리형 (Factorized) 모델 구조

  • 공간 모듈과 시간 모듈을 별도로 처리하는 방식.
  • 시계열 데이터를 먼저 시간적으로 처리한 후 공간적으로 처리하거나, 반대로 공간적으로 처리한 후 시간적으로 처리한다.
  • 이산형(Discrete) 모델 예시
    • STGCN[54]
    • 공간적 처리를 먼저 수행한 후, 시간적 처리를 적용.
  • 연속형(Continuous) 모델 예시
    • STGODE (Spatio-Temporal Graph Ordinary Differential Equation) [74]
    • 연속적인 변화(ODE 방식)를 반영하여 시공간 데이터를 처리.

2. 결합형 (Coupled) 모델 구조

  • 공간 모듈과 시간 모듈이 서로 얽혀서(interleaved) 작동하도록 설계.
  • 한 번의 연산 과정에서 공간-시간 처리가 함께 이루어진다.
  • 이산형(Discrete) 모델 예시
    • DCRNN (Diffusion Convolutional Recurrent Neural Network) [68]
    • 공간 정보(그래프)를 활용하여 RNN 기반으로 시계열 패턴을 학습.
  • 연속형(Continuous) 모델 예시
    • MTGODE (Multiresolution Temporal Graph ODE) [23]
    • 연속적인 그래프 변화와 다중 해상도 분석을 적용하여 시계열 패턴을 학습.

요약

  • STGNN 모델 아키텍처는 이산적(Discrete) 또는 연속적(Continuous) 방식으로 나뉜다.
  • 또 분리형(Factorized)과 결합형(Coupled)으로 나뉜다.
  • 분리형(Factorized) 모델: 공간과 시간을 순차적으로 처리. (예: STGCN, STGODE)
  • 결합형(Coupled) 모델: 공간과 시간을 동시에 처리. (예: DCRNN, MTGODE)
  • 다른 연구에서는 이를 "시간-공간(Time-then-Space)" vs. "동시 처리(Time-and-Space)"로 구분하기도 한다.

4. General Pipeline


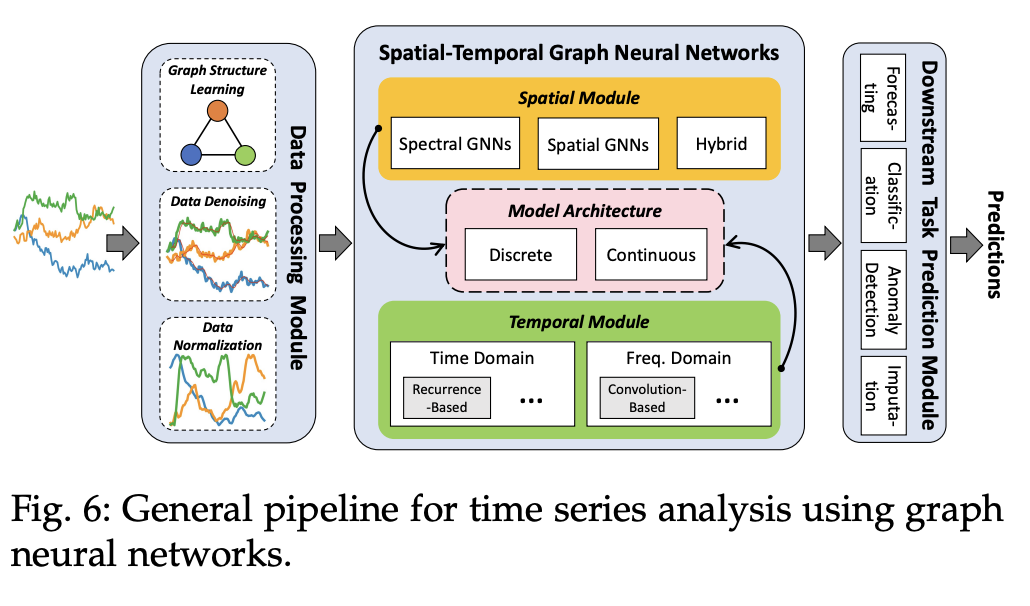
그림6은 STGNN을 활용한 시계열 분석의 일반적인 파이프라인을 보여준다.

파이프라인 진행 순서는 다음과 같다:
1. 데이터 전처리 (Data Processing Module)

  • 입력 데이터: 시계열 데이터셋
  • 주요 작업
    • 데이터 정제(Data Cleaning)
    • 정규화(Normalization)
    • 시계열 데이터의 위상 정보(Topology) 추출
      • 그래프 구조 생성 (노드 및 엣지 설정)

2. STGNN을 활용한 시계열 표현 학습

  • STGNN을 이용하여 시계열 데이터를 공간-시간적 표현(spatio-temporal representations)으로 변환.
  • 학습된 시계열 표현은 이후 다양한 분석 작업에 활용 가능하다.

3. 다운스트림 예측 작업 (Downstream Task Prediction Module)

  • STGNN이 생성한 시계열 표현을 기반으로 다양한 예측 및 분석 작업 수행.
  • 대표적인 다운스트림 작업:
    • 시계열 예측 (Forecasting)
    • 이상 탐지 (Anomaly Detection)

요약
데이터 전처리 -> GNN 적용 -> 분석
1. 데이터 전처리 → 정제, 정규화, 그래프 구조 생성.
2. STGNN 적용 → 시공간적 특징 학습.
3. 다운스트림 분석 → 예측, 이상 탐지 등 다양한 작업 수행.

4. GNNs FOR TIME SERIES FORECASTING

시계열 예측은 과거 관측 데이터를 기반으로 미래의 시계열 값을 예측하는 작업을 의미한다.

1. 기존 딥러닝 기반 시계열 예측의 한계

  • 딥러닝 모델은 비선형(Nonlinear) 시공간 패턴을 효과적으로 포착하여 기존 선형 모델보다 우수한 예측 성능을 보여준다.
  • 하지만 LSTNet [111] 및 TPA-LSTM [112]과 같은 기존 딥러닝 기반 모델은 시계열 간의 dynamic spatial correlations를 명확하게 반영하지 못하는 한계가 있다.

2. GNN(Graph Neural Network) 기반 예측 모델의 등장

  • 최근에는 그래프 신경망(GNN)-기반 모델이 등장하여 다변량 시계열(Multivariate Time Series)의 공간적·시간적 의존성을 명확하고 효과적으로 모델링하면서, 예측 성능이 더욱 향상되었다.

3. GNN 기반 시계열 예측 모델의 분류

  • GNN 기반 예측 모델은 다양한 관점에서 분류할 수 있다.
  1. 예측 대상(Task) 기준)
    • Multi-step forecasting
      • 과거 데이터를 기반으로 여러 개의 연속된 미래 시점을 예측.
      • 대부분의 모델이 이 방식을 사용.
    • Single-step forecasting
      • 과거 데이터를 기반으로 다음 또는 특정 한 시점의 값을 예측.
      • 상대적으로 연구가 적음.
  2. 방법론(Methodology) 기준)
    • 공간적(Spatial) 의존성 모델링
      • 변수 간의 관계(Inter-variable relationships)를 학습하여 공간적 상관관계 모델링.
      • 시간적(Temporal) 의존성 모델링
      • 시계열 내에서 시간에 따른 변화 패턴을 학습.
    • 공간-시간(Spatio-temporal) 모듈 융합
      • 공간적 & 시간적 패턴을 결합하여 시계열 예측 성능 극대화.

요약

  • 기존 딥러닝 모델은 공간적 상관관계를 명확히 반영하지 못하는 한계가 있다.
  • 반면 GNN 기반 모델은 공간적 & 시간적 의존성을 명확하게 학습하여 예측 성능을 향상시킨다.
  • 예측 모델은 multi-step vs. single-step으로 구분할 수 있으며, 공간-시간 관계를 어떻게 모델링하느냐에 따라 접근 방식이 달라진다.
  • spatial + temporal -> spatial-temporal

4.1 Modeling Inter-variable Dependencies

1. 공간적 의존성이 중요한 이유

  • 시계열 데이터에서 변수 간 상호작용(inter-variable relationships)이 예측 결과에 큰 영향을 미친다.
  • 각 시계열 변수가 서로 얼마나 밀접하게 연결되어 있는지를 나타내는 그래프 구조(graph structures)를 통해 더 정교한 예측이 가능하다.

2. 공간적 의존성을 모델링하는 방법

  • 현재 연구에서는 공간적 의존성을 모델링하기 위해 다음 세 가지 방법을 활용한다.
  1. 스펙트럴 GNN (Spectral GNNs)
    • 그래프 신호 처리(Graph Signal Processing) 이론을 기반으로, 그래프의 Frequency domain에서 관계를 학습.
    • 그래프 라플라시안(Graph Laplacian) 같은 변환을 활용하여 노드 간 관계를 포착.
  2. 공간적 GNN (Spatial GNNs)
    • 각 노드의 이웃(neighborhood) 정보를 직접 활용하여 공간적 관계를 모델링.
    • 메시지 패싱(Message Passing)과 그래프 확산(Graph Diffusion) 기법을 활용.
  3. 하이브리드 모델 (Hybrid Approach)
    • 스펙트럴 GNN과 공간적 GNN을 결합하여 두 방법의 장점을 모두 활용.

3. GNN 기반 공간 모델링의 수학적 표현

  • 입력 변수 XtX_t (시간 tt에서의 시계열 데이터)와 AtA_t (해당 시점의 그래프 구조)가 주어졌을 때,
    공간적 의존성을 학습하는 GNN 기반 모델을 SPATIAL(·) 이라고 정의할 수 있다.
  • 이 모델의 목표는 다양한 시계열 데이터에서 중요한 패턴을 효과적으로 포착하는 것이다.
    이를 수식으로 표현하면 다음과 같다:
    Xt^=SPATIAL(Xt,At)\hat{X_t} = SPATIAL(X_t, A_t)
    용어의 의미는 다음과 같다:
    • Xt^\hat{X_t} : 공간적 의존성이 반영된 시계열 표현(Embedding).
    • SPATIAL(Xt,At)SPATIAL(X_t, A_t) : 입력 데이터 XtX_t와 그래프 AtA_t를 이용하여 공간적 특징을 학습하는 함수.

요약

  • 변수 간 관계(공간적 의존성)는 시계열 예측 모델의 성능에 큰 영향을 미친다.
  • 연구에서는 스펙트럴 GNN, 공간적 GNN, 하이브리드 모델을 활용하여 공간적 의존성을 학습한다.
  • 최종적으로, GNN 기반 모델은 공간적 특징을 포함한 새로운 시계열 표현 Xt^\hat{X_t}을 생성하여 예측 성능을 향상시킨다.

1. Spectral GNN-based Approaches

초기 GNN 기반 시계열 예측 모델들은 주로 Chebyshev 다항식(Chebyshev polynomials)을 활용하여 그래프 합성곱(Graph Convolution)을 근사하는 ChebConv 기법을 사용했다. 이를 통해 변수 간(inter-variable) 관계를 모델링할 수 있었다.

1. 주요 스펙트럴 GNN 모델

  1. STGCN (Spatio-Temporal Graph Convolutional Network)
    • 시간적 합성곱(Temporal Convolution) + ChebConv 레이어를 조합.
    • 공간적(Spatial) 및 시간적(Temporal) 패턴을 함께 학습하는 구조.
  2. StemGNN (Spectral-Temporal Graph Neural Network)
    • ChebConv과 Frequency Domain 합성곱 신경망(CNN)을 결합.
    • ChebConv을 이용해 공간적 관계를 모델링.
    • 푸리에 변환(Fourier Transform)과 같은 frequency transform을 활용하여 시계열 패턴을 학습.

2. 추가적인 연구 흐름

초기 연구들이 ChebConv을 사용한 이후, 다양한 확장이 이루어졌다.
다음과 같은 요소들이 기존 모델에 추가되면서 더 정교한 예측 모델이 등장했다.

  1. 어텐션 메커니즘 (Attention Mechanisms)
    • 노드 간 관계를 더 유연하게 학습
    • 특정 시점에서 중요한 변수(노드) 간 관계를 강조하여 모델링
  2. 멀티 그래프 구성 (Multi-Graph Construction)
    • 서로 다른 유형의 관계를 고려한 여러 개의 그래프를 생성
    • 예: 거리 기반 그래프, 기능(feature) 기반 그래프 등
  3. 어텐션 + 멀티 그래프 결합 모델
    • 멀티 그래프를 활용하면서 어텐션 메커니즘을 추가하여, 변수 간 관계를 더욱 정교하게 모델링

요약

  • 초기 GNN 기반 시계열 예측 모델은 ChebConv을 사용하여 공간적 관계(변수 간 관계)를 학습했다.
  • STGCN과 StemGNN 같은 모델이 등장하며, 시공간 패턴을 동시에 학습하는 방식이 발전했다.
  • 이후 연구에서는 어텐션, 멀티 그래프 구조를 추가하여 모델의 성능을 더욱 향상시키는 방향으로 발전하고 있다.

2. Spatial GNN-based Approaches

최근 공간 GNN(Spatial GNNs)이 성공을 거두면서, 변수 간(inter-variable) 관계를 모델링하기 위해 메시지 패싱(Message Passing) 및 그래프 확산(Graph Diffusion) 기법을 사용하는 연구가 활발해졌다.

스펙트럴 GNN과 비교했을 때, 공간 GNN은 상대적으로 단순한 방식으로 그래프 구조를 학습하지만, 특정 노드 주변의 강한 국소적 유사성(local homophily)을 강조하는 특성이 있다.

1. 주요 공간 GNN 모델

  1. DCRNN (Diffusion Convolutional Recurrent Neural Network)
    • 그래프 확산 레이어(graph diffusion layers)를 활용.
    • GRU (Gated Recurrent Unit)와 결합하여 시계열 데이터를 모델링.
  2. Graph WaveNet
    • 그래프 확산 레이어를 시간적 합성곱(Temporal Convolution)과 결합하여, 공간 및 시간 의존성을 모두 학습.
  3. STGCN(1st)(두 번째 버전) & STMetaNet
    • 기존 STGCN과 달리 GCN (Graph Convolutional Network)과 GAT (Graph Attention Network)을 적용.
    • 인접한 시계열 노드(변수)에서 정보를 집계(aggregation).

2. 공간 GNN 모델의 발전 방향

공간 GNN 모델의 학습 능력을 향상시키기 위해 다양한 개선 모델들이 제안되었다.

  1. STSGCN (Spatial-Temporal Synchronous Graph Convolution)
    • 기존 GCN을 확장하여, 국소적 공간-시간 그래프(localized spatial-temporal graphs)에서 공간 및 시간 의존성을 동기적으로 학습.
  2. MTGODE (Multivariate Time-series Graph ODE) & TPGNN (Temporal Polynomial Graph Neural Network)
    • 연속적 그래프 전파(Continuous Graph Propagation) 방식 도입.
    • TPGNN은 시간적 다항 계수(Temporal Polynomial Coefficients) 기반 그래프 전파.
  3. 그래프 트랜스포머 (Graph Transformer) & 하이퍼그래프 (Hypergraphs) 기반 접근법
    • 기존 GCN보다 더 긴 범위의 공간 의존성(Long-range Spatial Dependencies) 학습 가능.
    • 전역 수용영역(Global Receptive Field)을 가지므로, 보다 넓은 관계를 포착할 수 있음.

요약

  • 공간 GNN 기반 모델은 메시지 패싱 및 그래프 확산 기법을 활용하여 변수 간 관계를 학습하는 접근법이다.
  • 초기 모델(예: DCRNN, Graph WaveNet)은 그래프 확산을 GRU 또는 합성곱과 결합하여 시간적 패턴을 학습했다.
  • 이후 GCN, GAT, 그래프 트랜스포머, 하이퍼그래프 등의 개념이 적용되면서, 더 긴 범위의 공간 관계까지 모델링할 수 있는 방법으로 발전하고 있다.

3. Hybrid Approaches

일부 하이브리드 모델은 스펙트럴 GNN과 공간 GNN을 결합하여 두 가지 접근법을 모두 활용한다.

1. 하이브리드 모델 예시

  1. SLCNN
    • ChebConv와 지역 메시지 패싱(localized message passing)을 결합하여
      전역적 및 지역적 합성곱을 통해 다양한 수준에서 공간 관계를 캡처.
      • ChebConv: Chebyshev 다항식을 이용한 스펙트럴 GNN.
      • 지역 메시지 패싱: 공간 GNN 기법으로, 특정 노드의 이웃에서 정보를 전파.
  2. AutoSTGNN
    • 신경망 아키텍처 검색(Neural Architecture Search, NAS)을 통합하여 최고 성능의 GNN 기반 예측 모델을 자동으로 식별하는 방식.

요약

  • 하이브리드 모델들은 스펙트럴 GNN과 공간 GNN의 장점을 결합하여, 더 효과적으로 시계열 예측을 위한 변수 간 관계를 모델링한다.
  • SLCNN은 전역 및 지역적 합성곱을 통해 다양한 공간적 패턴을 캡처하고,
  • AutoSTGNN은 신경망 아키텍처 검색을 통해 최적의 모델을 찾는 접근법을 사용한다.

4.2 Modeling Inter-temporal Dependencies

시간 의존성(Temporal Dependency) 모델링은 GNN 기반 시계열 예측에서 매우 중요한 요소이다.
이러한 시간적 패턴은 크게 시간(Time) 또는 Frequency 도메인으로 구분된다.

1. 시간 의존성 모델의 목적

  • 단일 시계열 데이터 XnX_n이 주어졌을 때, 이를 효과적으로 모델링하는 TEMPORAL(·) 모델을 학습하는 것.
  • 학습된 모델을 통해 입력 시계열 XnX_n 을 변환하여, 시간 의존성이 반영된 표현 X^nX̂_n 을 얻는 것.
    X^n=TEMPORAL(Xn)X̂_n = TEMPORAL(X_n)

2. 시간 의존성 모델링 방법

  1. 시간(Time) 도메인 접근법
    • CNN 기반 모델 → 합성곱을 이용해 시간 패턴을 포착
    • Attention 기반 모델 → 주목할 만한 시간 패턴을 강조
    • RNN 기반 모델 → LSTM, GRU 등을 이용하여 순차적인 시간 의존성을 모델링
  2. Frequency 도메인 접근법
    • 푸리에 변환(Fourier Transform) 등을 사용하여 시간 정보를 frequency 성분으로 변환한 후 분석
  3. 하이브리드(Hybrid) 접근법
    • 시간 + frequency 도메인 통합
    • CNN + Attention 등 다양한 모델 결합
      (예: 합성곱으로 지역적 시간 패턴을 포착한 후, 어텐션으로 장기 의존성 학습)

요약

  • 시계열 예측을 위한 GNN 기반 방법에서, 시간적 패턴은 시간 또는 frequency 도메인 접근법으로 나눨 수 있다.
  • 하이브리드 모델은 이러한 방법들을 결합하여 더 강력한 시간 의존성 학습을 수행한다.

1. Recurrent Models

초기 시계열 예측 모델에서는 순환 신경망(Recurrent Models) 을 활용하여 시간적 의존성(Inter-Temporal Dependency) 을 학습했다.
이러한 모델들은 주로 GRU(Gated Recurrent Unit) 와 GNN 을 결합하여 시간-공간(Spatial-Temporal) 관계를 효과적으로 모델링한다.

1. 주요 순환 모델 기반 접근법

  1. DCRNN (Diffusion Convolutional Recurrent Neural Network)
    • 교통 데이터 예측을 위해 개발된 모델.
    • 그래프 확산(Graph Diffusion) 기법과 GRU를 결합하여 시간-공간 종속성을 모델링.
  2. AGCRN (Adaptive Graph Convolutional Recurrent Network)
    • GRU와 GCN(Graph Convolutional Network)을 결합.
    • 그래프 구조를 학습하는 Graph Structure Learning 모듈 포함.
    • 기존 GCN보다 더 효율적으로 그래프 구조를 학습하는 Factorized GCN 활용.
  3. GTS (Graph Time Series model) & RGSL (Recurrent Graph Structure Learning)
    • 그래프 구조 학습(Graph Structure Learning, GSL) 에 초점을 맞춘 모델.
    • GCN, GRU를 활용하지만, 그래프 구조 학습 방법론에 따라 차이가 존재한다.

요약

  • 초기 연구들은 순환 신경망(GRU)과 그래프 신경망(GNN) 을 결합하여
    시간-공간 관계를 효과적으로 학습하는 방법을 제안했다.
  • 최근 연구들은 그래프 구조 학습(GSL)에 집중하여 더욱 발전된 모델을 제시하고 있다.

2. Convolution Models

위 순환 신경망(RNN)과 달리, 합성곱 신경망(CNN) 은 더 효율적인 방식으로 시간적 의존성(Inter-Temporal Dependency) 을 모델링할 수 있다.
대부분의 연구는 시간 영역(Time Domain) 에서 CNN을 활용하며, 일부는 Frequency Domain 을 활용하기도 한다.

1. 주요 합성곱 신경망 기반 접근법

  1. STGCN (Spatio-Temporal Graph Convolutional Network)
    • 1D 합성곱(1-D CNN) + Gated Linear Units (GLU) 를 활용한 Temporal Gated Convolution 제안.
    • CNN을 통해 시간적 패턴을 효과적으로 학습.
    • 모델 학습이 더 효율적이고 안정적.
  2. MTGNN (Multivariate Time-series Graph Neural Network) & MTGODE
    • 다변량 시계열 데이터(Multivariate Time-Series)를 학습하는 그래프 기반 CNN 모델.
    • 그래프 신경망(GNN)과 CNN을 결합하여 시간-공간(Spatial-Temporal) 관계를 학습.
  3. StemGNN (Spectral-Temporal Graph Neural Network) & TGC (Temporal Graph Convolution)
    • 기존 CNN과 달리 Frequency Domain에서 시간적 패턴을 모델링.
    • 시계열 데이터를 푸리에 변환(Fourier Transform)하여 frequency 특성 분석.

요약

  • CNN 기반 접근법은 RNN보다 병렬 연산이 가능해 학습 속도가 빠르다.
  • 대부분 시간 영역에서 활용되지만, 일부 모델은 frequency 영역을 활용하여 패턴을 분석하기도 한다.
  • STGCN, MTGNN, MTGODE 등은 CNN을 기반으로 시간적 패턴을 학습한다.
  • StemGNN, TGC 는 frequency 기반 접근으로 더 심층적인 시간적 관계를 학습한다.

3. Attention Models

최근에는 어텐션 메커니즘(Attention Mechanism)을 활용하여 시간적 상관관계(Temporal Correlation)를 효과적으로 학습하는 연구가 증가하고 있다.
특히, Transformer 모델(Self-Attention 기반)이 대표적인 예시이다.

1. 주요 Attention 기반 접근법

  1. GMAN (Graph Multi-Attention Network)
    • 공간(Spatial) 및 시간(Temporal) 정보를 함께 고려하여 과거 데이터를 어텐션 메커니즘으로 통합.
    • 트래픽 예측등의 시계열 데이터에 활용.
  2. ST-GRAT (Spatio-Temporal Graph Recurrent Attention Network)
    • Transformer 구조를 기반으로 한 모델.
    • 공간 주의 메커니즘(Spatial Attention Mechanism)을 추가하여 시계열 데이터 내의 시간-공간 패턴을 학습.
  3. STEP (Spatio-Temporal Enhanced Predictor)
    • Transformer 레이어를 활용하여 단변량(Univariate) 시계열 데이터의 시간 의존성 모델링.

요약

  • 어텐션 기반 접근법은 시계열 데이터에서 과거 패턴을 더 효과적으로 학습한다.
  • Transformer 구조(Self-Attention)를 활용하여 장기 의존성(Long-Term Dependencies) 학습에 강점이 있다.
  • GMAN, ST-GRAT, STEP 같은 모델들이 시간적/공간적 관계를 동시에 고려하는 방식으로 발전했다.

4. Hybrid Models

하이브리드(Hybrid) 모델은 여러 기법을 결합하여 시계열 데이터의 시간적 관계를 효과적으로 학습하는 방법이다.
이러한 모델들은 어텐션(Attention), 컨볼루션(Convolution), 순환신경망(Recurrent Networks) 등을 조합하여 지역(Local) 및 전역(Global) 시간 의존성을 함께 포착한다.

1. 주요 Hybrid 접근법

  1. ASTGCN (Attention-based Spatio-Temporal Graph Convolutional Network)
    • 시간 어텐션(Temporal Attention)과 컨볼루션(Convolution)을 결합.
    • 시계열 데이터에서 중요한 시간적 특징을 동적으로 강조.
    • 트래픽 예측 등의 문제에서 활용됨.
  2. DSTAGNN (Dynamic Spatio-Temporal Aware Graph Neural Network)
    • 시간적 어텐션 + 컨볼루션을 동시 적용.
    • 시간에 따라 변화하는 동적 시계열 관계를 효과적으로 학습.
  3. STGNN
    • GRU (Gated Recurrent Unit) + Transformer 결합.
    • 단기(Local) 및 장기(Global) 시간 의존성을 모두 고려.
    • 복잡한 시계열 데이터 패턴을 더욱 정교하게 모델링.
  4. TGC (Temporal Graph Convolution) - 비선형 변형(Nonlinear Variant)
    • Frequency Domain에서 Spectral Attention + Convolution 결합.
    • 시간적 패턴을 frequency 도메인에서 추출하여 학습.

요약

  • Hybrid 모델은 어텐션, 컨볼루션, 순환신경망을 조합하여 다양한 시간 패턴을 학습한다.
  • 또한, 지역(Local) 및 전역(Global) 시간 관계를 함께 고려한다.
  • 시간 도메인과 frequency 도메인을 모두 활용하는 방식으로 발전 중이다.
  • 트래픽 예측, 금융 시계열 예측 등 복잡한 시계열 문제 해결에 유용하다.

5. Forecasting Architectural Fusion

시계열 데이터에서 공간(SPATIAL(·)) 및 시간(TEMPORAL(·)) 의존성을 효과적으로 모델링하는 네 가지 신경망 구조 유형은 다음과 같다.
(1) 이산 분리형(Discrete Factorized), (2) 이산 결합형(Discrete Coupled), (3) 연속 분리형(Continuous Factorized), (4) 연속 결합형(Continuous Coupled)

1. 이산(Discrete) 모델
이산 모델은 시공간 의존성을 개별적인 단계에서 학습한다.

  1. 이산 분리형 (Discrete Factorized)
    • 공간(SPATIAL)과 시간(TEMPORAL) 모델을 독립적으로 학습
    • 두 모듈이 각각 따로 동작하며, 나중에 결합하여 예측 수행.
    • 일반적으로 공간 GNN + 시간 CNN/RNN 등으로 구성.
    • 예: 공간 GCN과 시간 RNN을 따로 학습한 후 결합.
  2. 이산 결합형 (Discrete Coupled)
    • 공간 및 시간적 관계를 하나의 프로세스에서 함께 모델링.
    • GNN과 RNN/CNN을 결합하여 하나의 네트워크에서 처리.

2. 연속(Continuous) 모델
이산 모델과 달리 신경 미분 방정식(Neural Differential Equations)을 활용하여 연속적인 모델링 과정을 적용한다.

  1. 연속 분리형 (Continuous Factorized)
    • 공간 및 시간적 관계를 각각 다른 연속적인 과정으로 학습.
    • 일부 혹은 전체 모델링 프로세스가 연속적으로 동작.
    • 예: Neural ODE 기반 모델이 각각 공간과 시간 패턴을 학습.
  2. 연속 결합형 (Continuous Coupled)
    • 하나의 연속적인 과정에서 공간과 시간 패턴을 동시에 학습.
    • Neural ODE를 기반으로 한 하나의 프로세스에서 모든 시공간 의존성을 처리.
    • 예: MTGODE (Multivariate Time Graph ODE)

요약

  • 이산 모델(Discrete Models) → 독립적(분리형) or 통합적(결합형) 방식으로 공간-시간 관계를 학습.
  • 연속 모델(Continuous Models) → Neural ODE를 활용하여 (독립 or 결합) 연속적인 방식으로 학습.
  • 연속 결합형(Continuous Coupled)이 가장 복잡하지만 가장 강력한 시공간 의존성 모델링 가능.
  • 실제 적용 사례에 따라 독립적 학습(분리형) vs. 통합적 학습(결합형) 선택.

6. Discrete Architectures

보통 많은 GNN 기반 시계열 예측 모델들은 이산 데이터(discrete data)를 처리하는 모델들이다.
이러한 모델들은 크게 이산 분리형(Discrete Factorized) 과 이산 결합형(Discrete Coupled) 으로 나뉜다.

1. 이산 분리형 (Discrete Factorized) 모델

  • 공간(GNN)과 시간(TEMPORAL) 모델을 독립적으로 처리하는 방식.
  • 일반적으로 그래프(GCN) + 시계열 모델(CNN/RNN)을 조합하여 예측.

대표적인 모델들

  • DGCNN (Dynamic Graph Convolutional Neural Network)
    → 동적 그래프 구조(dynamic graph structure)를 추정하여 예측 성능 향상.
  • HGCN (Hierarchical Graph Convolutional Network)
    → 계층적 그래프 구조(hierarchical graph generation)를 도입하여 성능 개선.

2. 이산 결합형 (Discrete Coupled) 모델

  • 공간(GNN)과 시간(TEMPORAL) 모듈을 하나의 프로세스로 통합하여 학습
  • 그래프 확산(diffusion) 또는 어텐션(attention) 메커니즘을 활용하여 시공간 의존성 학습.

대표적인 모델들

  • DCRNN (Diffusion Convolutional Recurrent Neural Network)
    → 그래프 확산(Graph Diffusion) + GRU 기반 순환 모델을 조합하여 교통 데이터 예측.
  • MRA-BGCN (Multi-Resolution Adaptive BGCN)
    → 다중 해상도(Multi-Resolution) 방식으로 공간-시간 관계 학습
  • RGSL (Recurrent Graph Structure Learning)
    → 재귀적 구조 학습을 통해 시계열 데이터를 모델링.

3. 어텐션(Attention) 기반 결합형 모델
일부 연구에서는 공간 및 시간적 어텐션 메커니즘(Attention Mechanism)을 하나의 모듈로 통합하여 성능을 향상시켰다.

대표적인 모델

  • GMAN (Graph Multi-Attention Network)
    → 공간 및 시간 어텐션 메커니즘을 게이트 방식(Gated)으로 결합하여 시계열 패턴을 효과적으로 학습.

요약

  • 이산 데이터 처리 방식에는 크게 이산 분리형(Discrete Factorized) 과 이산 결합형(Discrete Coupled)으로 나뉜다.
  • 이산 분리형: 공간과 시간 모듈을 독립적으로 학습.
  • 이산 결합형: 공간과 시간을 하나의 프로세스로 결합하여 학습.
  • 어텐션 기반: 공간+시간+어텐션 연산을 하나의 모듈로 통합.

7. Continuous Architectures

현재까지 연속형(Continuous) 모델에 속하는 연구는 많지 않지만, 일부 방법들이 있다.
연속형 모델은 크게 연속 분리형 (Continuous Factorized) 과 연속 결합형 (Continuous Coupled) 으로 나뉜다.

1. 연속 분리형 (Continuous Factorized) 모델

  • 공간(GNN)과 시간(TEMPORAL) 모듈을 독립적으로 학습.
  • 그래프 전파(Graph Propagation)를 연속적인 과정(Continuous Process)으로 모델링.

대표적인 모델

  • STGODE (Spatio-Temporal Graph Ordinary Differential Equation)
    → 그래프 전파 과정을 NODE(Neural ODE)로 연속적으로 모델링.
    → 시간 축을 따라 팽창 합성곱(Dilated Convolution) 을 적용하여 장기 의존성(Long-range Dependencies) 학습.

2. 연속 결합형 (Continuous Coupled) 모델

  • 공간(GNN)과 시간(TEMPORAL) 모듈을 하나의 연속적인 과정으로 통합하여 학습.
  • 일반적으로 두 개 이상의 NODE 또는 NCDE 를 활용하여 시공간 의존성을 모델링.

대표적인 모델

  • MTGODE (Multivariate Time-series Graph ODE)
    → 공간(GNN)과 시간(TEMPORAL) 모델을 하나의 통합된 NODE 프로세스로 결합
  • STG-NCDE (Spatio-Temporal Graph Neural Controlled Differential Equation)
    → NODE 대신 NCDE(Neural Controlled Differential Equation) 프레임워크를 사용.
    → NCDE를 활용하면 연속적인 외부 입력(External Control Signal)과 함께 공간-시간 의존성을 학습 가능.

요약

  • 연속형 모델은 크게 연속 분리형과 연속 결합형으로 구분된다.
  • 연속 분리형: graph propagation을 연속적인 과정으로 모델링. (시간 따로, 공간 따로)
  • 연속 결합형: graph propagation 과정을 NODE로 연속적인 과정으로 모델링. (시간+공간 같이)

5. GNNs FOR TIME SERIES ANOMALY DETECTION

시계열 이상 탐지란 정상적인 데이터 생성 과정에서 벗어난 데이터 관측값을 식별하는 과정이다.
이상치는 다음과 같이 분류될 수 있다:

  • 단일 이상치(Point Anomaly) : 개별적인 데이터 포인트가 이상한 경우.
  • 구간 이상치(Subsequence Anomaly) : 특정 연속된 데이터 구간이 이상한 경우.

그러나 다음과 같은 이유로 시계열 데이터에서 이상치를 정의하는 것은 쉽지 않다:

  • 이상치는 매우 드물어(label이 적어) 수집과 라벨링이 어렵다.
  • 모든 종류의 이상치를 미리 정의하는 것은 불가능하다.

따라서 지도 학습(Supervised Learning)은 적용이 어렵고, 비지도 학습(Unsupervised Learning)이 주로 활용된다.

1. 전통적인 이상 탐지 기법
초기에는 거리 기반(Distance-based) 기법과 확률 분포 기반(Distributional) 기법이 주로 사용되었다.

  • 거리 기반: 데이터 포인트 간의 유사도를 계산하여 이상치를 감지.
  • 분포 기반: 데이터가 특정 확률 분포를 따른다고 가정하고, 이를 벗어나는 데이터를 이상치로 감지.

하지만 복잡한 시계열 패턴을 감지하는 데 한계가 있다.

2. 딥러닝 기반 이상 탐지 기법
최근에는 딥러닝 모델을 활용한 이상 탐지가 발전하면서 재구성(Reconstruction) 및 예측(Forecasting) 전략이 많이 사용된다.

재구성 기반 모델 (Reconstruction-based)

  • 정상 데이터를 학습한 모델이 입력 데이터를 다시 복원하도록 훈련.
  • 만약 이상치 데이터가 입력되면 제대로 재구성되지 않음 → 이를 이상으로 판단.

예측 기반 모델 (Forecasting-based)

  • 정상 데이터를 학습한 모델이 미래 데이터를 예측.
  • 만약 예측값과 실제값 간의 오차가 크면 이상으로 판단.

이러한 순환 신경망(Recurrent Models) 기반 모델은 이상 탐지에서 중요한 역할을 하지만, 변수 간의 관계(Interdependence)를 명확히 모델링하지 못하는 단점이 있다.

3. 그래프 신경망(GNN) 기반 이상 탐지
최근에는 GNN(Graph Neural Networks)의 시공간(Spatial-Temporal) 의존성을 모델링하는 능력과 관련하여 이상 탐지에서 주목받고 있다.

  • GNN은 기존 RNN 모델의 한계를 극복하며 복잡한 이상 패턴을 탐지할 수 있다
  • 변수 간의 관계를 명확히 표현
  • 시공간적 특성을 효과적으로 학습

요약

  • 이상 탐지(Anomaly Detection): 정상적인 데이터 패턴에서 벗어난 데이터를 식별하는 과정.
  • 지도학습은 한계가 있어 비지도 학습(Unsupervised Learning)이 주로 활용된다.
  • 전통적인 거리 기반 및 확률 분포 기반 기법은 한계가 있다.
  • 딥러닝 모델(RNN 등)은 재구성 및 예측 오류를 활용하여 이상 탐지를 잘 수행한다.
  • 그러나 RNN 기반 모델은 변수 간의 관계를 명확히 모델링하지 못하는 한계가 있다.
  • 최근 GNN 기반 모델이 이러한 한계를 보완하며 이상 탐지에서 강력한 성능을 보이고 있다.

5.1 General Approach to Anomaly Detection

unsupervised learing으로 이상 탐지를 수행하려면 모델이 주어진 데이터에서 정상(Normal) 패턴을 학습해야 한다.
이를 위해 딥러닝 모델은 일반적으로 두 가지 주요 모듈로 구성된 구조를 사용한다.

1. 이상 탐지 모델의 구조
이상 탐지 모델 = ① 백본(Backbone) 모듈 + ② 스코어링(Scoring) 모듈

  1. 백본 모듈 (Backbone Model)
    • BACKBONE(·): 주어진 훈련 데이터를 학습하는 모델.
    • 훈련 데이터는 대부분 정상 데이터(또는 아주 적은 이상 데이터 포함)로 가정한다.
    • 이 모델은 데이터의 정상적인 패턴을 학습하고, 입력 데이터에 대한 출력 데이터를 생성한다.
  2. 스코어링 모듈 (Scoring Module)
    • SCORER(X, Xˆ ): 백본 모듈의 출력 Xˆ 과 실제 데이터 X를 비교하여 이상 점수(Anomaly Score)를 계산.
    • 이상 점수는 예측된 신호(Xˆ)와 실제 신호(X) 간의 차이(Discrepancy)를 측정한 값이다.
    • 일반적으로, 특정 변수가 정상적인 기대치에서 크게 벗어나면 이상치로 판단된다.

2. 이상 탐지 모델의 작동 방식

  1. 백본 모델이 데이터를 학습하고, 예측값 Xˆ 를 생성
    • 예: 백본 모델이 GNN 기반의 시계열 예측기(GNN Forecaster)라면, 다음 스텝의 데이터를 예측한다.
  2. 스코어링 모듈이 X 와 Xˆ 를 비교하여 이상 점수를 계산
    • 이상 점수 계산 방식:
      ∑i=1N∣xi,t−x^i,t∣\sum_{i=1}^{N} |x_{i,t} - \hat{x}_{i,t}|
      • NN: 채널(변수)의 개수
      • xi,tx_{i,t}: 실제 시계열 데이터의 i번째 변수 값
      • x^i,t\hat{x}_{i,t}: 예측된 시계열 데이터의 i번째 변수 값
      • ∣xi,t−x^i,t∣|x_{i,t} - \hat{x}_{i,t}|: 각 변수별 예측 오차(에러)
  3. 최종 이상 점수는 모든 변수의 예측 오차를 합산하여 계산된다.
    • 특정 변수의 예측 오차가 크다면 해당 변수가 이상치의 원인(Root Cause)이 될 가능성이 높다.
    • 이를 통해 이상 감지뿐만 아니라, 어떤 변수가 문제를 유발했는지도 분석 가능하다.

3. 최근 연구 동향
최근에는 GNN(Graph Neural Networks)을 활용한 백본 및 스코어링 모듈이 발전하면서, 더욱 정교한 이상 탐지 모델들이 제안되고 있다.

  • GNN 기반 백본 모델은 복잡한 시공간 패턴을 학습하는 데 강점이 있다.
  • GNN 기반 스코어링 모듈은 변수 간 관계를 고려하여 더 정밀한 이상 탐지가 가능하다.

요약

  • 비지도 학습 기반 이상 탐지는 정상 데이터를 학습하고, 이상 점수를 통해 이상치를 탐지하는 방식.
  • 백본 모델(Backbone)이 정상 패턴을 학습하고, 스코어링 모듈(Scorer)이 예측 오차를 기반으로 이상을 판단.
  • 최근 GNN을 활용한 이상 탐지 모델이 발전하면서 더욱 효과적인 탐지 및 원인 분석이 가능해졌다.

5.2 Discrepancy Frameworks for Anomaly Detection

대부분의 이상 탐지 모델은 동일한 백본-스코어러 아키텍처(Backbone-Scorer architecture)를 따른다.
하지만 백본 모듈이 정상 데이터에서 데이터 구조를 학습하는 방식과 스코어링 모듈의 구현 방식에 따라 세 가지 범주로 구분된다.
(1) 재구성(Reconstruction)
(2) 예측(Forecast)
(3) 관계 불일치(Relational discrepancy)

1. Reconstruction Discrepancy

Reconstruction Discrepancy(재구성 불일치) 프레임워크는 정상 시점에서는 재구성 오류가 낮고, 이상 시점에서는 오류가 크다는 가정 하에 작동한다.
이 모델은 입력을 출력으로 복원(reconstruction)하려는 방식으로 설계되며, 오토인코더(autoencoders)와 유사하다.

  1. 백본(Backbone) 모델

    • 백본 모델은 훈련 데이터의 분포를 잘 모델링하고 재구성하는 역할을 한다.
    • 하지만 훈련 데이터에 포함되지 않은(out-of-sample) 데이터에는 잘 대응하지 못한다.
    • 이를 위해 저차원 임베딩 코드를 강제하거나 변분 목표(variational objectives)를 사용하는 제약과 정규화 과정이 포함될 수 있다.

  2. Reconstruction Discrepancy와 이상 탐지

    • 모델이 정상 시점에서는 입력을 잘 복원하지만, 이상 시점에서는 Reconstruction Discrepancy가 커지게 된다.
    • 그 후, 스코어링 모듈(SCORER)이 재구성된 출력과 실제 데이터를 비교하여 불일치 점수(discrepancy score)를 계산하여 이상을 식별한다.

  3. GNN과 다른 모델의 차이점

    • Deep Reconstruction Discrepancy Model은 일반적으로 이러한 원칙을 따르지만, GNN을 사용하는 모델은 백본 reconstructor가 STGNN으로 구현되어 있다는 점에서 차별화된다.
    • 예를 들어, MTAD-GAT와 LSTM-VAE는 모두 변분 목표(variational objectives)를 사용하지만, MTAD-GAT는 그래프 어텐션 네트워크(GAT)를 사용하여 공간적-시간적 의존성을 학습한다.
    • 그 외에도 VGCRN과 FuSAGNet 같은 유사한 연구들도 있다.

  4. 그래프 수준 임베딩

    • 또 다른 연구 방향은 그래프 수준 임베딩을 활용하여 입력 그래프 데이터를 벡터로 표현하고, 이를 통해 다변량 시계열에 대해 잘 확립된 이상 탐지 방법을 적용하는 것이다.

요약

  • Reconstruction Discrepancy 모델은 정상 데이터를 잘 복원하고, 이상 데이터에서는 Reconstruction Discrepancy가 커지는 방식을 이용해 이상을 탐지한다.
  • GNN 기반의 모델은 공간적-시간적 의존성을 학습하는 데 강점을 가지며, 변분 목표(variational objectives)와 그래프 어텐션 네트워크(GAT) 등을 활용한다.
  • 그래프 수준 임베딩을 통해 다변량 시계열 이상 탐지를 향상시키려는 접근이 활발히 연구되고 있다.

2. Forecast Discrepancy

Forecast Discrepancy 프레임워크는 정상 시점에서는 예측 오차가 낮고, 이상 시점에서는 예측 오차가 크다는 가정 하에 작동한다. 이 모델에서는 백본(Backbone) 모델이 GNN 예측기(GNN Forecaster)로 대체되며, 이 forecaster는 한 스텝 앞의 예측을 하도록 훈련된다.

  1. 백본 모델: GNN 예측기(GNN Forecaster)

    • GNN 예측기는 한 스텝 앞의 예측을 수행한다.
    • 배포 시, 예측기는 한 스텝 앞의 예측을 하고, 그 예측값은 스코어링 모듈(Scorer)로 전달된다.

  2. 스코어링 모듈: 예측 오차 비교

    • 스코어링 모듈은 예측값을 실제 관측 신호와 비교하여 예측 불일치를 계산한다.
    • 예측 불일치는 보통 절대 오차(abs error) 또는 평균 제곱 오차(MSE)와 같은 방식으로 계산된다.

  3. 이상 탐지

    • 이상 시점에서는 입력 데이터가 정상 패턴에서 벗어나, 예측과 실제 값의 차이가 커져서 예측 불일치가 크게 발생하게 된다.

  4. 대표적인 예시: GDN

    • GDN은 그래프 구조 모듈과 그래프 어텐션 네트워크를 사용하여 입력 시계열을 한 스텝 앞의 예측으로 인코딩하고, 예측 오차의 maximum absolute forecast error를 계산하여 이상을 감지한다.

  5. Forecast Discrepancy vs Reconstruction Discrepancy

    • Reconstruction Discrepancy 모델은 현재 입력을 잠재 공간으로 투영하고 재구성하는 방식으로, 재구성이 실패할 때 이상을 탐지한다.
    • 반면, Forecast Discrepancy은 과거 데이터를 사용해 현재 값을 예측하고, 예측과 실제 관측치를 비교하여 예측 오류를 기반으로 이상을 탐지한다.
    • Reconstruction 모델은 현재 입력을 복제하는 데 집중하는 반면, Forecasting 모델은 미래 데이터를 예측하고 예측 오류를 통해 이상을 탐지하는 데 중점을 둔다는 차이가 있다.

  6. 고급 Forecast Discrepancy 모델

    • GST-Pro와 같은 고급 예측 불일치 모델은 실제 관측값 없이도 이상을 예측할 수 있으며, 이는 미래 시간에 대한 이상 예측을 가능하게 한다.

요약

  • Forecast Discrepancy 모델은 과거 데이터를 기반으로 미래의 값을 예측하고, 예측 오류를 통해 이상을 탐지.
  • Reconstruction Discrepancy 모델은 현재 입력을 복제하려고 시도하고, 재구성 오류를 통해 이상을 탐지.
  • Forecast Discrepancy 모델은 예측 오류에 의존하며, 예측 오차가 큰 시점에서 이상을 탐지하고, 고급 모델은 실제 관측 없이도 미래의 이상을 예측할 수 있다.

3. Relational Discrepancy

Relational Discrepancy(관계 불일치) 프레임워크는 정상 시점과 이상 시점에서 변수 간 관계가 크게 변한다는 가정을 기반으로 작동한다.

  1. 핵심 개념
    • 시계열 데이터의 변수 간 관계(Relationships)가 정상일 때는 일정한 패턴을 유지하지만, 이상 시점에서는 관계가 급격히 변화한다.
    • STGNN(Spatial-Temporal Graph Neural Network)의 특성을 활용하여 그래프 구조를 학습하고, 이를 통해 이상 탐지 및 진단을 수행한다.
  2. 구성 요소
    • 백본(Backbone): 그래프 학습 모듈(Graph Learning Module)
      • 숨겨진 변수 간 관계 변화를 학습하고, 시계열 데이터를 기반으로 동적으로 그래프 구조를 생성한다.
    • 스코어링 모듈(Scorer): 관계 변화 평가
      • 변수 간 관계(Relationships)의 변화를 분석하여 이상 점수(Anomaly Score)를 계산한다.
  3. 대표적인 모델
    • GReLeN
      • 동적으로 그래프 구조를 생성하여 이상을 탐지하는 모델.
      • 입력 시계열 데이터를 기반으로 각 시간별 그래프 구조를 만들고, 노드의 In-degree, Out-degree 변화를 분석하여 이상을 감지.
    • DyGraphAD
      • 예측 기반(Forecasting-based) 접근 방식.
      • 다변량 시계열 데이터를 여러 개의 하위 시퀀스(Subsequences)로 분할.
      • 이를 동적으로 변화하는 그래프(Dynamically Evolving Graphs)로 변환한 후, 한 스텝 앞의 그래프 구조를 예측하여, 실제 그래프와 비교한다.
      • 스코어링 모듈이 예측된 그래프와 실제 그래프 간의 차이(관계 불일치, Relational Discrepancy)를 계산하여 이상을 탐지한다.

요약

  • 관계 불일치(Relational Discrepancy) 모델은 변수 간 관계가 정상 시점과 이상 시점에서 변화한다는 가정을 기반으로 작동.
  • 그래프 학습 모듈(Backbone)이 동적 그래프 구조를 생성하여 변수 간 관계 변화를 모델링.
  • 스코어링 모듈(Scorer)이 변수 관계의 변화량을 계산하여 이상을 탐지.
  • 대표적인 모델
    • GReLeN: 동적으로 그래프 구조를 생성하고, 노드의 In-degree, Out-degree 변화를 통해 이상 감지.
    • DyGraphAD: 그래프 예측 기반 모델로, 한 스텝 앞의 그래프 구조를 예측하고 실제 그래프와의 차이를 이상 신호로 판단.

4. Hybrid and Other Discrepancies

  • 각 불일치(Discrepancy) 기반 프레임워크는 서로 다른 유형의 이상을 탐지하는 데 강점이 있다.
  • 관계(Relational) 불일치: 서로 다른 채널 간의 관계 패턴을 분석하여 공간적 이상(Spatial Anomalies)을 탐지. (예: GDN 모델)
  • 예측(Forecast) 불일치: 시계열 데이터의 급격한 변화(Spikes)나 시즌성 불일치(Seasonal Inconsistencies)를 효과적으로 감지.

따라서, 다양한 불일치 기법을 조합하여 더욱 정교한 이상 탐지 모델을 만들 수 있다.

1. 하이브리드(Hybrid) 접근 방식
여러 가지 불일치(Discrepancy) 기법을 결합하여 STGNN(Spatial-Temporal Graph Neural Networks)의 강점을 극대화할 수 있다.

  • MTAD-GAT:
    • 재구성(Reconstruction) 불일치 + 예측(Forecast) 불일치를 결합하여 이상 탐지 성능 향상.
  • DyGraphAD:
    • 예측(Forecast) 불일치 + 관계(Relational) 불일치를 함께 사용하여 시계열 및 관계적 이상 탐지.

2. 사전 지식(Prior Knowledge) 활용
기존 불일치 기반 접근 방식 외에도, 사전 지식(Prior Knowledge)을 활용하여 이상 탐지 성능을 높일 수 있다.

  • 예: GraphSAD
    • 훈련 데이터에서 6가지의 이상 유형을 정의하고, 이를 가짜 레이블(Pseudo Labels)로 생성.
    • 원래는 비지도 학습 기반 이상 탐지(Unsupervised Anomaly Detection) 문제였지만, 이를 분류(Classification) 문제로 변환하여 학습.
    • 이 과정에서 클래스 간 불일치(Class Discrepancy)를 이상 탐지 지표로 활용.

요약

  • 서로 다른 불일치 기반 접근 방식은 각기 다른 유형의 이상을 감지하는 데 강점이 있다.
  • 하이브리드 방식을 통해 여러 불일치 방법을 결합하면 더욱 강력한 이상 탐지 모델을 구축할 수 있다.
    • MTAD-GAT: 재구성 + 예측 불일치 결합
    • DyGraphAD: 예측 + 관계 불일치 결합
  • 사전 지식 활용(GraphSAD 등)을 통해 이상 탐지 모델을 비지도(Unsupervised) → 지도(Supervised) 방식으로 변환할 수도 있다.

6. GNNs FOR TIME SERIES CLASSIFICATION

시계열 분류(TSC)는 주어진 시계열 데이터의 패턴을 분석하여 특정 Label을 할당하는 것이다.

1. 기존 연구 동향
과거 시계열 분류 연구는 다음과 같은 두 가지 접근 방식을 중심으로 발전해 왔다.

  • 거리 기반(Distance-based) 방법
    • 유사한 시계열 패턴을 찾기 위해 Dynamic Time Warping (DTW) 등의 거리 측정 기법을 활용.
  • 앙상블(Ensemble) 방법
    • 여러 개의 개별 모델을 조합하여 성능을 향상하는 기법.
    • 대표적인 방법으로 Random Forest 또는 Bagging Ensemble 등이 있다.

문제점:

  • 기존 방법들은 고차원(High-dimensional) 데이터나 대규모 데이터셋(Large-scale dataset)에 적용할 때 확장성(Scalability) 관련 문제점이 있다.

2. 딥러닝을 활용한 새로운 접근 방식

  • 기존 방법들의 한계를 극복하기 위해 딥러닝 기반 방법이 연구되고 있다.
  • 특히 Graph Neural Networks(GNNs)을 활용하면 시계열 데이터를 그래프(Graph) 형태로 변환하여 강력한 패턴 분석이 가능하다.
    • GNN의 장점
      • 국소(Local) 및 전역(Global) 패턴을 동시에 학습 가능.
      • 다양한 시계열 데이터 간의 관계(Relationships)를 효과적으로 모델링할 수 있다.

최근 연구에서 Foumani et al. [154]가 TSC에 대한 최신 서베이를 발표했지만, GNN 적용 사례는 다루지 않고 있다.
따라서, GNN의 단변량(Univariate) 및 다변량(Multivariate) 시계열 분류 문제를 새롭게 분석할 필요가 있다.

요약

  • 시계열 분류(TSC)는 주어진 시계열 데이터의 패턴을 분석하여 특정 라벨을 할당하는 문제.
  • 기존 연구는 거리 기반 방법(Distance-based Methods)과 앙상블 기법(Ensemble Methods)에 집중되었으나, 대규모 데이터에서의 확장성 문제가 있다.
  • 이를 해결하기 위해 딥러닝 기반 방법, 특히 GNN(Graph Neural Networks)을 활용하는 접근 방식이 주목받고 있다.
  • GNN을 사용하면 시계열 데이터를 그래프로 변환하여 더 정교한 패턴 분석과 관계 학습이 가능하다.

6.1 Univariate Time Series Classification

1. 시계열 분류 vs. 다른 시계열 분석 기법
시계열 분류(TSC)는 기존의 시계열 분석 기법과 근본적으로 다른 목표를 가진다.

  • 일반적인 시계열 분석 기법
    • 시계열 예측(Forecasting): 미래 값을 예측하는 것에 초점.
    • 이상 탐지(Anomaly Detection): 실시간으로 이상 징후를 탐지하는 것에 초점.
    • 이들은 데이터 내부의 패턴을 학습하여 시계열의 변화 양상을 모델링하는 것이 목표.

반면, 시계열 분류(TSC)는

  • 샘플 간의 패턴 차이를 학습하여 각 샘플을 특정 클래스(Label)로 구분하는 것이 핵심 목표이다.
  • 즉, 데이터 내부의 패턴을 분석하는 것이 아니라 샘플 간의 차이를 찾아내는 것에 집중한다.

2. 새로운 그래프 기반 접근 방식
연구자들은 단변량(Univariate) 시계열 분류 문제를 해결하기 위해 그래프(Graph) 기반의 새로운 접근법을 제안한다.

  • Series-as-Graph
    • 시계열 데이터를 하나의 그래프로 변환하여 시간적 관계(Temporal Relationships)와 패턴을 그래프 구조에서 학습하는 방법.
  • Series-as-Node
    • 개별 시계열 샘플을 하나의 노드(Node)로 간주하고, 샘플 간의 관계를 그래프 형태로 학습하는 방법.

요약

  • 시계열 분류(TSC)는 기존 시계열 분석 기법과 달리 샘플 간의 차이를 분석하여 라벨을 예측하는 것이 목표.
  • 예측(Forecasting)이나 이상 탐지(Anomaly Detection)처럼 데이터 내부 패턴을 학습하는 것이 아니다.
  • 새로운 그래프 기반 방법(Series-as-Graph, Series-as-Node)을 통해 시계열 데이터를 효과적으로 학습하는 접근법이 연구되고 있다.

1. Series-as-Graph

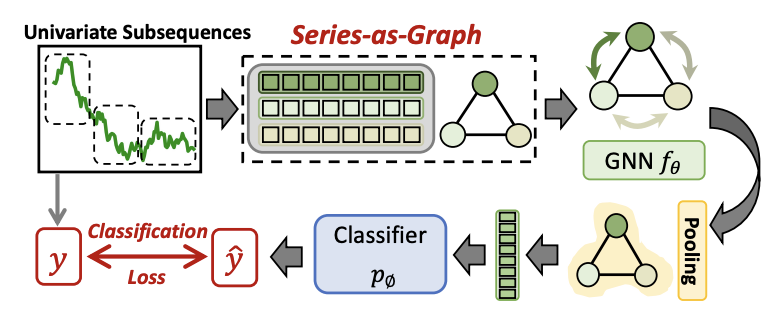
Series-as-Graph는 단변량(Univariate) 시계열 데이터를 그래프로 변환하여 GNN(Graph Neural Network)을 활용해 분류한다.

  • 핵심 아이디어: 시계열 내의 패턴을 그래프 구조로 변환하여 학습 가능하게 만드는 것.
  • 각 시계열을 그래프 노드들(여러 개의 시계열 집합)로 나누고, 이들 간의 관계를 엣지로 표현.
  • 이후 GNN을 적용하여 그래프 분류(Graph Classification) 문제로 해결.

1. 대표 연구 사례

  1. Time2Graph+
    • Time2Graph에서 발전된 모델로, GNN을 활용하여 시계열을 효과적으로 학습한다.
    • 모델링 과정 (2단계)
      1. Shapelet Graph 변환: 시계열을 shapelet(특징이 되는 부분 시퀀스) 기반의 그래프로 변환한다.
      2. GNN 적용: 그래프 구조에서 shapelet 간의 관계를 학습하고, 그래프 풀링(Graph Pooling) 기법을 사용해 전체 시계열의 전역 표현(Global Representation)을 생성한다.
    • 이 전역 표현을 분류기(Classifier)에 입력하여 최종 클래스 라벨을 예측한다.
  2. EC-GCN
    • 암호화된 네트워크 트래픽을 그래프로 변환하여 분류하는 방식으로 응용된다.

요약

  • Series-as-Graph는 시계열 데이터를 그래프로 변환하여 GNN을 활용한 분류를 수행한다.**
  • Time2Graph+는 대표적인 방법으로, shapelet 기반 그래프 변환 + GNN이 적용된 것이다.
  • Series-as-Graph 접근법은 다변량(Multivariate) 시계열 분류 문제에도 적용 가능하다.
  • 이상 탐지가 목적인 Series2Graph와는 다르게, Series-as-Graph는 분류(Classification)가 목적이다.

2. Series-as-Node

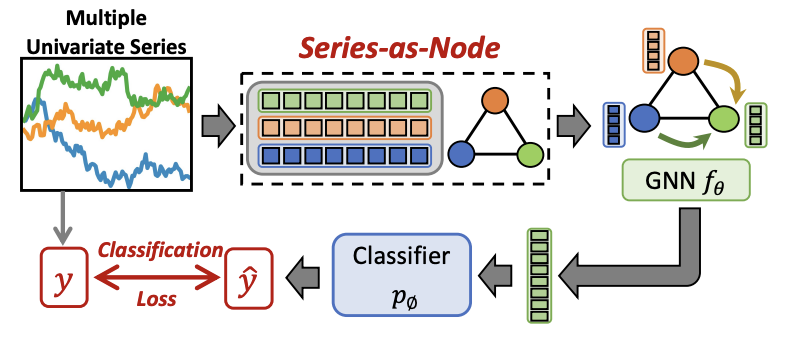
  • Series-as-Node는 각 시계열 샘플을 개별 노드(Node)로 간주하여 분류하는 접근법이다.
  • 서로 다른 시계열 샘플 간의 관계(Relationship)를 엣지(Edge)로 표현하여 전체 데이터를 하나의 큰 그래프로 구성한다.
  • 이 방식은 노드 분류(Node Classification) 문제로 변환되어 GNN을 활용한 학습이 가능하다.

주요 차이점

  • Series-as-Graph: 단일 시계열 내에서 패턴을 그래프로 변환 (Graph Classification).
  • Series-as-Node: 전체 시계열 데이터를 하나의 그래프에 표현하고 개별 시계열을 노드로 설정 (Node Classification).

1. 대표 연구 사례

  1. SimTSC
    • 각 시계열 샘플을 노드로 설정하고, 시계열 간의 유사도를 기반으로 엣지를 연결.
    • 노드 간 연결(엣지)은 DTW (Dynamic Time Warping) 거리를 사용하여 정의된다.
    • 이렇게 구성된 그래프에서 GNN을 사용하여 노드 분류(Node Classification)를 수행한다.
  2. LB-SimTSC
    • SimTSC를 확장한 모델로, DTW 계산의 효율성을 개선.
    • 기존 DTW의 시간 복잡도 O(L2)O(L^2)을 DTW의 Lower Bound를 활용하여 O(L)O(L)로 줄였다.
    • 계산 시간을 크게 단축하면서도 성능 유지.

2. 주요 특징 및 활용

  • 시계열 샘플 간의 관계를 활용하여 더 정교한 분류 가능.
  • 전체 데이터셋을 하나의 큰 그래프로 변환하여 전역적(Global) 관계를 학습.
  • DTW 거리 기반 그래프 구축 → LB-SimTSC으로 연산 최적화.

요약

  • Series-as-Node는 각 시계열을 노드로 보고, 샘플 간 관계를 그래프로 모델링하여 노드 분류 수행한다.
  • Series-as-Graph와 달리, 전체 데이터셋을 하나의 그래프에 표현하여 시계열 간의 관계를 학습한다.
  • SimTSC는 DTW 기반으로 노드 간 엣지를 설정하여 GNN을 활용한 분류 모델을 제안한다.
  • LB-SimTSC는 DTW 연산을 최적화하여 SimTSC의 계산 효율성을 높인 개선 모델이다.

6.2 Multivariate Time Series Classification

  • 다변량 시계열 분류는 단변량(Univariate) 시계열 분류와 기본적인 목표는 동일하나, 추가적인 복잡성이 존재한다.
  • 특히, 변수 간 상호작용(Inter-variable dependencies) 을 고려해야 한다는 것이 가장 큰 특징이다.
  • 예를 들어, 뇌 영역(brain regions) 간 상호작용을 분석할 때, 단일 노드만을 보면 전체 신경 활동을 온전히 이해할 수 없다.
  • 대신, 변수 간 관계를 효과적으로 모델링하면 신경 질환 여부와 같은 복잡한 패턴을 더 정확하게 분류 가능하다.

1. 변수 간 관계(Inter-variable Dependencies)와 그래프 모델링

  • 다변량 시계열 데이터의 변수 간 관계는 자연스럽게 네트워크 그래프로 표현 가능하다.
  • 이러한 그래프 구조는 GNN(Graph Neural Networks)을 활용하기에 적합하다.
  • GNN을 사용하면 고차원 데이터를 보다 의미 있는 표현(representation)으로 변환하여 효과적으로 분류 가능하다.

2. 핵심 목표

  • 고차원 시계열 데이터의 복잡성을 단순화하면서도 핵심 정보를 유지.
  • 변수 간 관계를 그래프로 모델링하여 더 정교한 분류 가능.
  • GNN을 활용하여 시계열 데이터를 효과적으로 표현하고 대표 클래스로 구분.

요약

  • 다변량 시계열 분류는 단변량 분류와 유사하지만, 변수 간 관계를 고려하는 것이 가장 큰 특징이다.
  • 예를 들어, 뇌 영역 간 상호작용을 모델링하면 신경 질환 여부를 효과적으로 분류 가능하다.
  • 변수 간 관계는 그래프로 표현할 수 있으며, GNN을 활용하면 더 정확한 분류가 가능하다.
  • 핵심 목표는 복잡한 고차원 데이터를 더 이해하기 쉬우면서도 표현력이 높은 형태로 변환하는 것이다.

7. GNNs FOR TIME SERIES IMPUTATION

  • TIME SERIES IMPUTATION(시계열 보간)은 데이터 포인트 시퀀스에서 결측값을 추정하는 방법이다.
  • 기존 시계열 보간 방법은 통계적 기법에 의존한다. 예를 들어 평균 보간(mean imputation), 스플라인 보간(spline interpolation), 회귀 모델(regression models) 등이 사용됐다.
  • 그러나 이러한 방법들은 복잡한 시간적 의존성(temporal dependencies)과 비선형 관계(non-linear relationships)를 잘 포착하지 못한다는 단점이 있다.

1. 딥러닝 기반의 시계열 보간

  • 딥러닝 기반의 방법은 위와 같은 일부 한계를 완화하였지만, 변수 간 의존성(inter-variable dependencies)을 명시적으로 고려하지 않는다.

2. GNN을 활용한 시계열 보간

  • 최근 GNN(Graph Neural Networks)의 등장으로, 공간적 및 시간적 의존성을 더 잘 포착하여 시계열 보간에서 새로운 가능성을 제시하고 있다.
  • GNN 기반의 시계열 보간은 크게 두 가지로 분류된다:
    1. In-sample Imputation: 주어진 시계열 데이터 내에서 결측값을 채우는 방법.
    2. Out-of-sample Imputation: 다른 시퀀스에서 결측값을 예측하는 방법.

3. GNN을 활용한 보간 방법론

  • 결정론적 접근(Deterministic Approaches): 결측값에 대해 단일 최적 추정값을 제공하는 방법.
  • 확률론적 접근(Probabilistic Approaches): 불확실성을 고려하여 가능한 값들의 분포(distribution)를 제공하는 방법.

요약

  • 기존의 시계열 보간 방법들은 복잡한 시간적 의존성이나 비선형 관계를 잘 포착하지 못한다는 제약이 있다.
  • GNN은 이러한 복잡한 의존성을 더 잘 포착하며, 인샘플 및 아웃오브샘플 보간 작업에 활용될 수 있다.
  • 결정론적 및 확률론적 방법론을 통해 GNN을 활용한 시계열 보간이 개선될 수 있다.

7.1 In-sample Imputation

In-sample Imputation은 주어진 시계열 데이터 내에서 결측값을 채우는 방법이다.
대부분의 기존 GNN 기반 방법은 In-sample Imputation에 집중하고 있다.

1. 주요 연구들

  • GACN:
    • 시공간적(spatial-temporal) 의존성을 모델링하기 위해 GAT와 시간적 합성곱 계층(temporal convolution layers)을 인코더에 결합.
    • 결측값을 채우기 위해 GAT와 시간적 디컨볼루션 계층(temporal deconvolution layers)을 결합하여 잠재 상태(latent state)를 원래의 특성 공간(feature space)으로 매핑.
  • GRIN:
    • 그래프 순환 보간 네트워크(Graph Recurrent Imputation Network)를 제안.
    • 각 단방향 모듈은 하나의 시공간 인코더와 두 개의 imputation executor로 구성.
    • 시공간 인코더는 MPNN(Message Passing Neural Network)과 GRU(Gated Recurrent Unit)를 결합.
    • 첫 번째 단계에서는 한 단계 앞의 예측값으로 결측값을 채우고, 두 번째 단계에서는 MPNN을 거쳐 정교화한다.
  • 기타 관련 연구:
    • AGRN, DGCRIN, GARNN, MDGCN 등은 양방향 순환 구조를 사용한 연구들로, 중간 처리 과정에서 차이가 있음.

2. 확률적 인샘플 보간(probalistic in-sample imputation)

  • 최근 확률적 인샘플 시계열 보간에 대한 연구도 일부 진행되고 있다.
  • 연구에서는 보간을 generation task로 간주하고 있다.

요약

  • In-sample Imputation은 GNN 기반 방법들이 주로 집중하는 분야로, 여러 연구에서 시공간적 의존성을 모델링하고, 순환 신경망(RNN)과 그래프 신경망(GNN)을 결합하여 결측값을 채우는 방법을 제시한다.
  • 또한, 확률적 접근법을 통해 보간을 generation task로 다루는 연구들도 등장하고 있다.

7.2 Out-of-sample Imputation

현재까지 GNN 기반의 방법 중 out-of-sample imputation에 속하는 연구는 매우 적다.

주요 연구들

  • IGNNK:
    • 유도형 GNN 크리깅 모델을 제안하여 관찰되지 않은 시계열 신호(예: 다변량 시계열에서 새로운 변수)를 복원.
    • 훈련 과정은 마스크된 서브그래프 샘플링과 diffusion GCN를 사용하여 신호를 복원하는 방식으로 진행된다.
  • SATCN:
    • IGNNK와 유사한 방법이지만, 기본 GNN 아키텍처에 차이가 있다.
  • INCREASE:
    • 이질적인 시공간 관계를 고려하여 유도형 시공간 크리깅 성능을 향상.
  • GRIN:
    • 인샘플과 아웃 오브 샘플 보간을 모두 처리할 수 있다.

요약

  • Out-of-sample Imputation을 다루는 GNN 기반 방법은 수가 매우 적다.
  • 주요 연구에는 IGNNK, SATCN, INCREASE, GRIN 등이 있다.

8. PRACTICAL APPLICATIONS AND RESOURCES

  • GNN4TS(Time Series Analysis for GNNs)는 다양한 분야에 적용되고 있으며, 주요 응용 분야는 다음과 같은 7개 영역으로 나눌 수 있다:
    1. Smart transportation(스마트 교통)
    2. On-demand services(주문형 서비스)
    3. Environment & sustainable energy(환경 및 지속 가능한 에너지)
    4. Internet-of-things(사물인터넷(IoT))
    5. Physical systems(물리 시스템)
    6. Healthcare(헬스케어)
    7. Fraud detection(이상 거래 탐지)
  • 이 섹션에서는 위의 분야 중 세 가지 주요 영역을 중심으로 논의하며, 자세한 내용은 부록 E에서 확인 가능하다.
  • 또한, 부록 F에서는 대표적인 모델의 오픈소스 구현과 공통 벤치마크 데이터셋에 대한 내용이 있다.

1. Smart Transportation

GNN의 발전으로 교통 분야가 크게 변화하고 있으며, 주요 응용 분야는 교통 예측과 항공편 지연 예측이 있다.

  • 교통 예측: 시공간 GNN(spatial-temporal GNN)을 활용하여 교통 상황을 보다 정확하게 예측할 수 있으며, 이를 통해 경로 계획 및 교통 체증 관리가 가능하다.
  • 교통 데이터 보간 (Imputation): 교통 데이터의 정확성을 유지하고 분석 및 예측 모델의 신뢰성을 높이기 위해 교통 데이터 복원 연구도 활발히 진행되고 있다.
  • 자율 주행 및 항공편 지연 예측: 자율 주행과 항공편 지연 예측에도 GNN이 적용되고 있으며, 이는 스마트 교통 시스템의 발전을 촉진한다.

2. Environment & Sustainable Energy

GNN은 풍력·태양광 발전 예측, 대기 오염 예측, 기상 예측 등 다양한 분야에서 활용되고 있다.

  • 풍속 및 풍력 발전량 예측: GNN은 복잡한 시공간적 바람 패턴을 효과적으로 모델링하여, 풍력 에너지 자원의 효율적인 관리에 기여한다.
  • 태양광 발전 예측: 태양광 발전량과 태양 복사량(solar irradiance) 예측을 위해 GNN이 사용되며, 태양광 발전에 영향을 미치는 여러 요인 간의 복잡한 관계를 모델링하여 높은 정확도의 예측을 제공한다.
  • 대기 오염 및 기상 예측: 대기 질 및 날씨를 예측하는 데에도 활용되며, 이는 농업, 에너지, 교통 등 다양한 산업에서 중요한 역할을 한다.

3. Physical systems

GNN은 상호작용하는 객체들로 구성된 다양한 물리 시스템을 모델링하는 데 효과적으로 활용되고 있다.

  • 천체 역학(n-body system) 시뮬레이션: GNN을 활용하여 다수의 천체가 중력에 의해 상호작용하는 시스템을 모델링하고 예측할 수 있다.
  • 입자 물리학(particle physics) 시뮬레이션: 입자의 상호작용을 그래프 구조로 표현하여 GNN을 적용하는 연구가 진행되고 있다.
  • 인체 동작 예측(human motion dynamics): 사람의 움직임을 모델링하여 동작을 예측하는 데 활용된다.
  • 분자 동역학(molecular dynamics) 예측: 분자 간의 물리적 상호작용을 시뮬레이션하여 신약 개발이나 재료 과학 연구에 응용된다.

4. Other Applications

GNN을 활용한 시계열 분석(Time Series Analysis) 연구는 다양한 분야로 확장되고 있다.

  • 금융(Finance): 주가 예측, 리스크 분석 등에 GNN이 활용된다.
  • 온디맨드 서비스(On-Demand Services): 배달 서비스 최적화 및 사용자 수요 예측에 적용된다.
  • 사기 탐지(Fraud Detection): 이상 거래 탐지를 통해 금융 사기 및 사이버 보안 강화에 기여한다.
  • 제조(Manufacturing): 생산 공정 최적화 및 장비 유지보수 예측에 활용된다.
  • 추천 시스템(Recommender Systems): 사용자 행동 데이터를 기반으로 맞춤형 추천 모델을 개선하는 데 사용된다.

이처럼 GNN을 활용한 시계열 분석(GNN4TS) 연구는 지속적으로 발전하고 있으며, 데이터 기반 의사결정 및 시스템 최적화(Data-Driven Decision Making & System Optimization)의 새로운 가능성을 열어가고 있다.

9. FUTURE DIRECTIONS

1. Pre-training, Transfer Learning, and Large Models

GNN을 활용한 시계열 분석(Time Series Analysis with GNNs)에서 사전 학습(Pre-training), 전이 학습(Transfer Learning), 그리고 대규모 모델(Large Models)이 중요한 기법으로 부상하고 있다. 이는 데이터가 부족하거나 다양성이 높은 환경에서 모델 성능을 향상시키는 데 기여한다.

  • 핵심 개념:
    • 한 도메인에서 학습한 표현을 다른 관련 도메인으로 전이하여 성능을 향상시키는 방식.
    • 기존의 학습된 지식을 활용하여 새로운 데이터에 대한 학습 효율을 증가시킴.
  • 주요 연구 사례:
    • Panagopoulos et al.: 데이터가 제한된 환경에서 COVID-19 예측을 위한 메타 러닝(Meta-Learning) 적용.
    • Shao et al.: 공간-시간 GNN(Spatial-Temporal GNN)을 위한 사전 학습 프레임워크 제안.
  • 현재 연구 동향:
    • 생성형 AI 및 대규모 모델(Generative AI & Large Models)이 발전하면서, 다양한 시간 시리즈 분석 작업에 적용 가능성이 증가.
    • 대규모 사전 학습 데이터 부족, 복잡한 공간-시간 관계 학습 전략 설계, 모델의 전이 가능성(Transferability) 보장 등의 도전 과제가 존재함.

2. Robustness

GNN의 강건성(Robustness)은 데이터의 변형(Data Perturbation)과 분포 변화(Distribution Shift)에 얼마나 잘 대응하는가를 의미하며, 특히 적대적 공격(Adversarial Attacks)에 대한 대응력이 중요하다.

  • 시간 시리즈 데이터에서의 중요성
    • 동적 시스템(Dynamic Systems)에서 발생하는 운영 실패(Operational Failures)는 시스템 전체의 무결성을 손상시킬 수 있다.
    • 예를 들어, 스마트 시티(Smart City)에서 데이터 노이즈 및 오류(Data Corruption)를 제대로 처리하지 못하면 교통 관리 시스템이 마비될 수 있다.
    • 의료(Healthcare) 분야에서는 잘못된 데이터 처리가 치료 시기의 누락을 초래할 수 있다.
  • 현재 연구 방향
    • GNN이 여러 응용 분야에서 우수한 성능을 보이지만, 강건성을 향상시키고 실패를 효과적으로 관리할 수 있는 전략 개발이 필수적이다.

GNN의 강건성을 개선하는 것은 시계열 분석의 신뢰성을 높이는 핵심 요소로, 연구가 지속적으로 진행되고 있다.

3. Privacy Enhancing

GNN이 다양한 산업에서 활용되면서 프라이버시 보호(Privacy Protection)의 중요성이 커지고 있다.

  • GNN의 특성과 프라이버시 문제
    • GNN은 복잡한 시스템 내 관계를 학습 및 재구성하는 능력이 있다.
    • 이는 시계열 데이터에서 개별 노드(Node) 및 관계(Edge)의 프라이버시 보호가 필수적임을 의미한다.
    • GNN의 해석 가능성(Interpretability)은 취약점을 파악하는 데 유용하지만, 동시에 민감한 정보가 노출될 위험성도 존재한다.
  • 프라이버시 보호와 GNN의 균형
    • GNN의 장점을 활용하면서도 강력한 프라이버시 보호를 유지하는 것이 중요하다.
    • 이를 위해 지속적인 연구와 혁신이 필요하며, 프라이버시 강화를 위한 다양한 접근법이 연구되고 있다.

GNN을 활용한 시계열 분석에서 데이터 보호와 분석 성능 간 균형을 맞추는 것이 핵심 과제로 떠오르고 있다.

4. Scalability

GNN은 복잡한 시계열 데이터 분석에 효과적이지만, 대량의 시계열 데이터를 처리하는 과정에서 메모리 제약과 같은 문제가 발생할 수 있다.

  • 기존 GNN의 확장성 문제 해결 방법
    • 노드 단위 샘플링(Node-wise sampling)
    • 레이어 단위 샘플링(Layer-wise sampling)
    • 그래프 단위 샘플링(Graph-wise sampling)
    • 위와 같은 샘플링 기법을 활용하면 메모리 부담을 줄일 수 있지만, 시간적 종속성(Temporal Dependency)을 유지하는 것은 여전히 어려운 과제이다.
  • 실시간 GNN 애플리케이션에서의 확장성 향상
    • 엣지 디바이스(Edge Devices)와 같이 계산 자원이 제한된 환경에서도 GNN을 효율적으로 실행할 필요가 있다.
    • 확장성과 실시간 추론(Real-time Inference) 문제를 해결하는 것은 중요한 연구 분야이며, 향후 큰 발전 가능성을 가지고 있다.

즉, GNN의 확장성을 높이면서도 시간적 종속성을 보존하는 것이 중요한 연구 과제로 떠오르고 있다.

10. CONCLUSIONS

이 서베이 논문은 GNN을 활용한 시계열 분석(Graph Neural Networks for Time Series, GNN4TS) 분야의 최신 연구 동향을 정리하며, 기존 연구들을 통합적으로 분류하였다.

1. GNN4TS의 주요 분석 과제

  • 시계열 예측(Forecasting)
  • 분류(Classification)
  • 이상 탐지(Anomaly Detection)
  • 결측치 보완(Imputation)
    위 네 가지 핵심 분석 과제를 다루며, 현재까지의 연구 발전 상황을 체계적으로 정리하였다.

2. GNN4TS 연구의 핵심 요소

  • 공간적(Spatial) 및 시간적(Temporal) 종속성 모델링
  • 모델 아키텍처의 세부 구조 분석
  • 개별 연구들에 대한 세밀한 분류 및 비교

3. GNN4TS의 확장성과 미래 전망

  • 다양한 산업 및 분야에서 GNN4TS의 적용 범위가 확장되고 있으며, 이를 통해 기술의 유연성과 성장 가능성을 확인할 수 있다.
  • 본 서베이는 GNN4TS의 연구 방향을 제안하고, 실무자 및 연구자들에게 가치 있는 자료를 제공하며 향후 연구를 위한 영감을 제시하였다.
profile
이재호
천천히, 그리고 꾸준히.
이전 포스트

[논문 리뷰] Multi-task self-supervised time-series representation learning

다음 포스트

[논문 리뷰] [부록 정리] A Survey on Graph Neural Networks for Time Series: Forecasting, Classification, Imputation, and Anomaly Detection

0개의 댓글