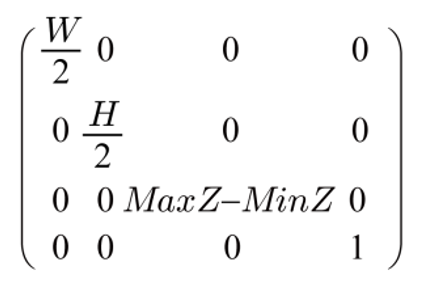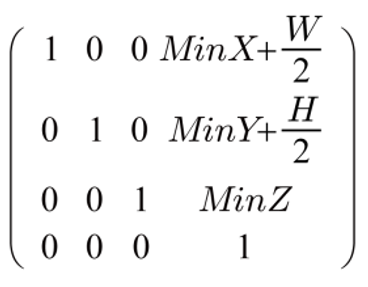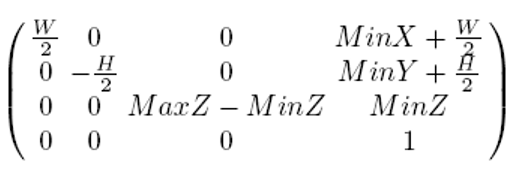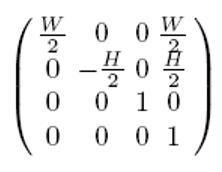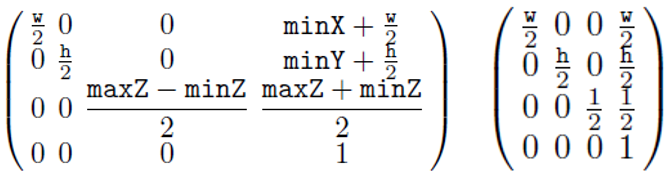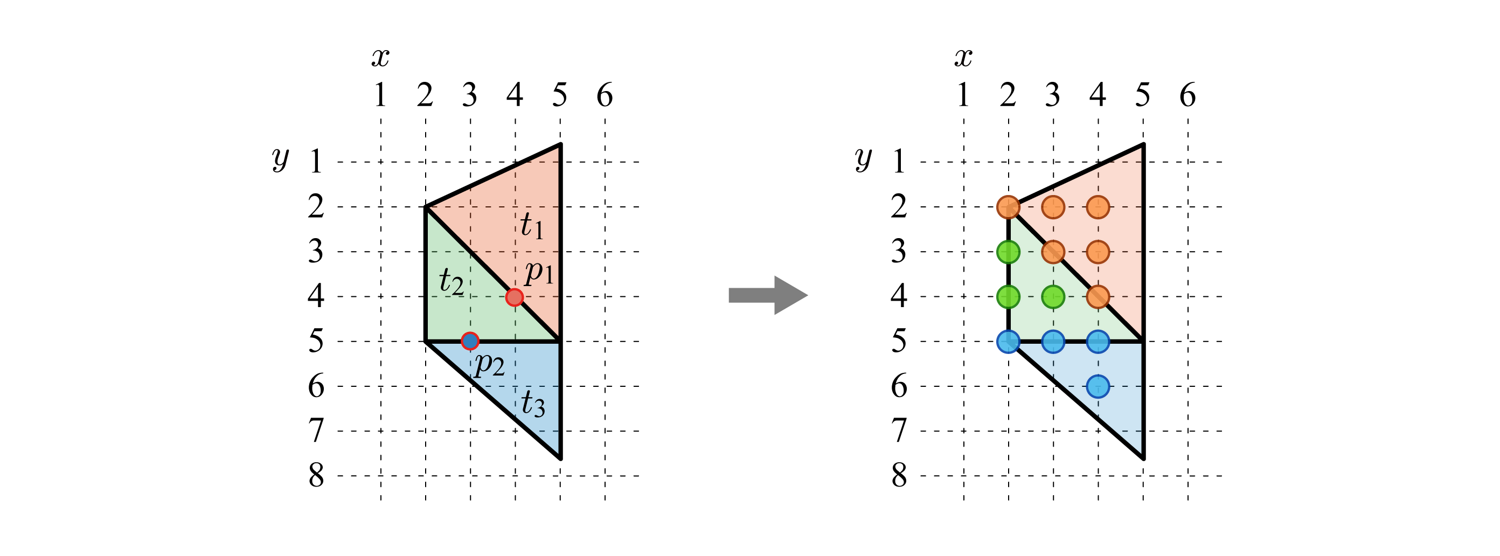이 시리즈는 3차원 그래픽스에 대해 공부한 내용들을 담고 있습니다.
참고 자료 :게임 프로그래밍을 위한 3차원 그래픽스 (한정현, 홍릉과학출판사),OpenGL ES를 이용한 3차원 그래픽스 입문 (한정현, 홍릉과학출판사)등
앞서 정점 처리Vertex processing 단계를 거쳐 처리된 vertex들은 primitive(점, 선, 삼각형 등)로 묶여 독자적인 개체로 취급된다.
2차원에 그려질 삼각형들의 vertex가 결정되면 primitive를 이루는 픽셀마다의 프래그먼트fragment가 생성된다.
이후 vertex에 할당되었던 여러 데이터를 보간하여 프래그먼트에 할당한다.
이는 래스터화Rasterization 단계에서 수행되는 작업이며, 본 포스트에서 다룰 내용에 대한 개괄이다.
위의 내용을 간단히 나열하면 다음과 같다.
- Primitive clipping
- Perspective Division
- Face Culling
- Viewport Transform
- Scan Conversion
래스터화 단계는 hardwired기 때문에 프로그래밍이 불가능하다.
Primitive Clipping
View frustum과 물체의 충돌 여부에 따라 view frustum 외부의 부분을 잘라내는 작업을 지칭한다.
이 때 view frustum 외부의 vertex는 소멸하며, view frustum과 객체가 교차하는 지점에는 새로운 vertex가 생성된다.
즉, 새로운 primitive가 생성된다.
Perspective division
NDC (Normalized Device Coordinates)
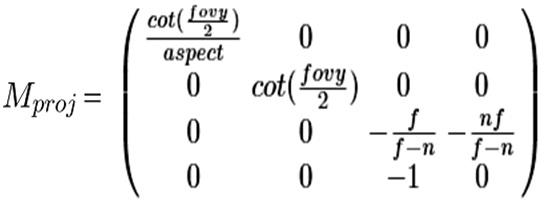
위의 행렬식은 projection transform에 사용되는 projection matrix이다.
Affine transform과는 다르게 4번째 행이 (0 0 -1 0)인데, 이로 인해 v = (x y z 1)에 를 적용하여 변환된 vertex v'의 w 좌표는 -z가 된다.
homogeneous coordinates 상의 좌표를 cartesian coordinates 상의 좌표로 변환하기 위해서 v'의 원소들을 w로 나누는 것을 원근 나눗셈perspective division이라고 한다.
또한, 이렇게 나눠진 좌표를 NDC(Normalized Device Coordinates)라고 부른다.
NDC의 범위는 (), ()로 나타난다.
이 때 앞서 말했듯 변환된 vertex v'에서 w = -z이고, 이는 곧 vertex로부터 xy평면까지의 수직거리와 같으므로 perspective division을 적용한 결과(NDC)는 원근법이 적용된 형태로 이해할 수 있다.
Face Culling
culling : 카메라에 보이지 않는 부분을 제거하는 작업
삼각형은 카메라를 향하는지 여부에 따라 앞면front-face인지, 뒷면back-face인지 정해진다.
이 여부는 삼각형의 vertex과 카메라의 위치 벡터(EYE)를 이은 벡터c와 삼각형의 노멀 벡터를 내적함으로써 쉽게 판별 가능하다.
다음은 내적dot product의 부호에 따른 서로 다른 두 벡터가 이루는 각도이다.
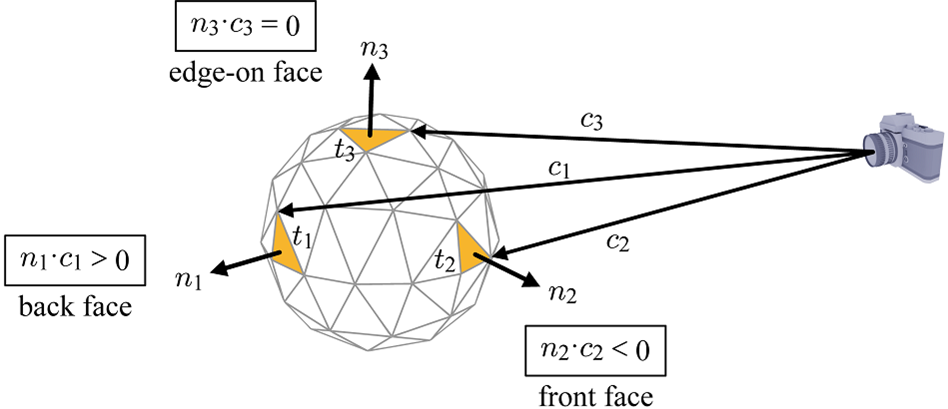
내적 결과가 양수가 나왔다는 것은 삼각형의 노멀벡터가 다음과 같이 c와 비슷한 방향(이루는 각이 예각)을 바라보고 있다는 뜻이다.
즉, 삼각형은 카메라를 등지고 있으므로 이 삼각형은 뒷면이다.
반대로 내적값이 음수인 경우 해당 삼각형은 카메라가 바라보는 방향을 마주보고 있음을 의미한다.
즉, 앞면의 삼각형이다.
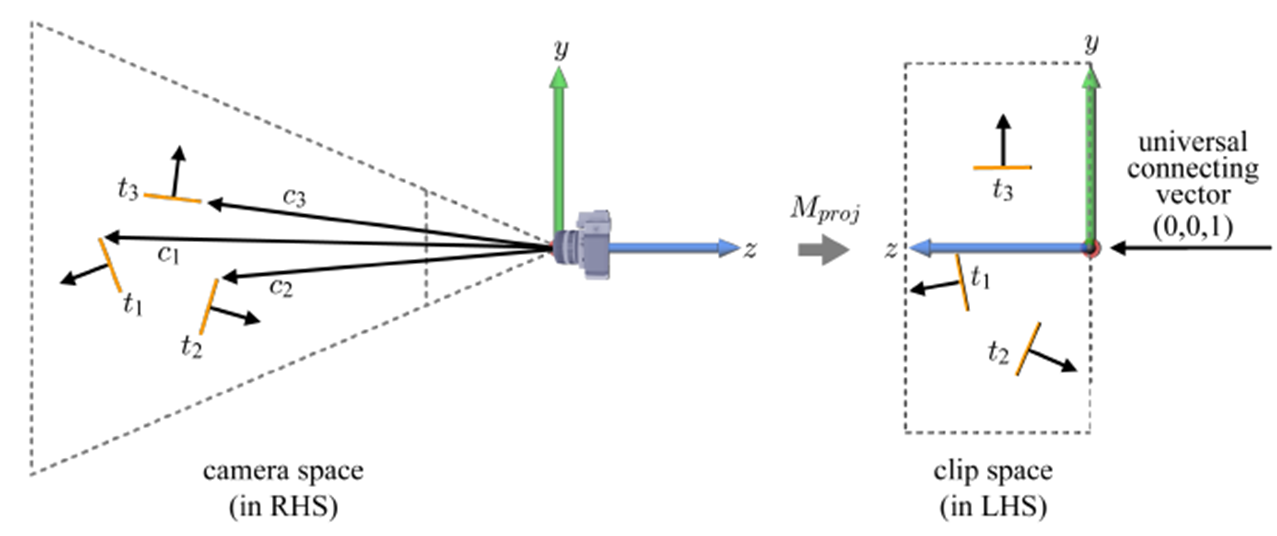
실제로는 모든 삼각형에 대해 위와 같이 연결 벡터 c를 구하지는 않는다.
그 이유는 camera space에서 clip space로 projection transform이 일어나고 나면 c를 하나의 연결 벡터로 나타낼 수 있기 때문이다.
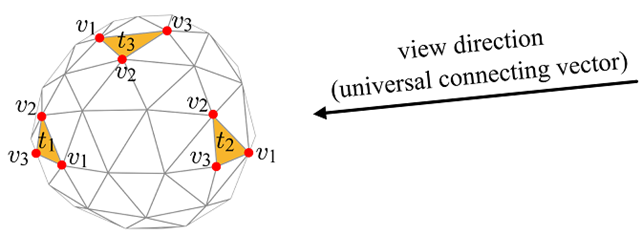
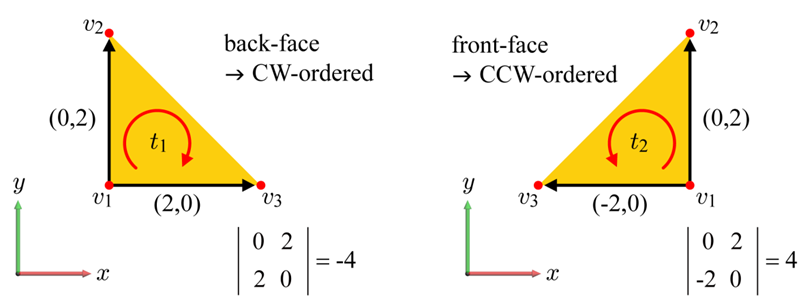
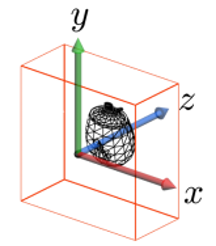
이러한 단일 연결 벡터를 통해 위의 그림과 같이 구를 이루는 삼각형을 바라볼 때, 구의 뒷면을 이루는 삼각형은 vertex의 순서가 시계 방향으로 구성되어 있고, 구의 앞면을 이루는 삼각형은 반시계 방향으로 구성되어 있다는 점을 관찰할 수 있다.
이는 해당 삼각형의 행렬식determinant를 통해 빠르게 구할 수도 있다.
행렬식의 결과가 음수라면 시계 방향(뒷면), 양수라면 반시계 방향(앞면)을 가지는 삼각형이다.
0이라면 삼각형의 변만 보인다는 것을 의미한다.
행렬 에 대한 determinant
단, 앞면으로 표시된 삼각형이 전부 렌더링되는 것은 아니다. 다른 앞면들에 가려질 수 있기 때문이다.
또한 뒷면 삼각형 역시도 렌더링될 수 있다. 반투명한 물체를 렌더링하기 위해서는 뒷면 삼각형 역시도 필요하다.
Viewport Transform
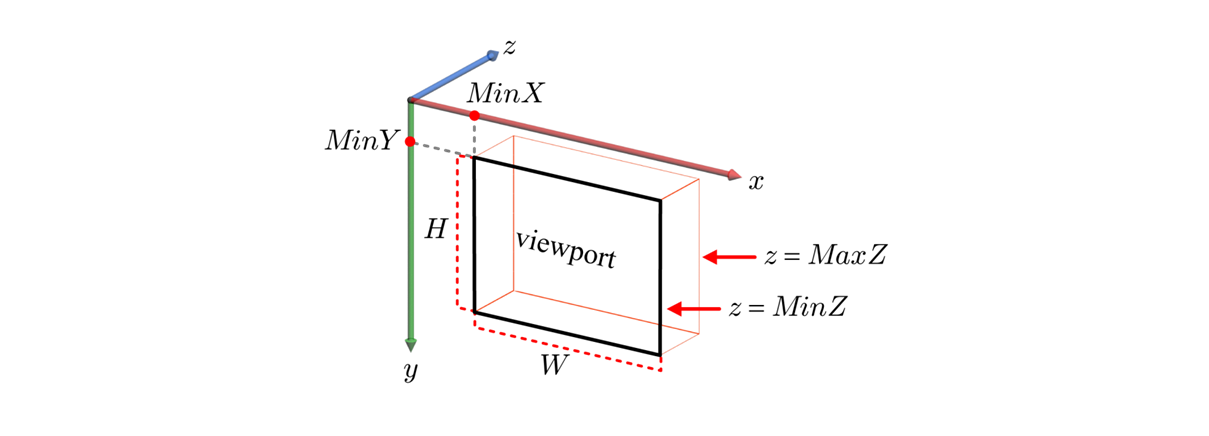
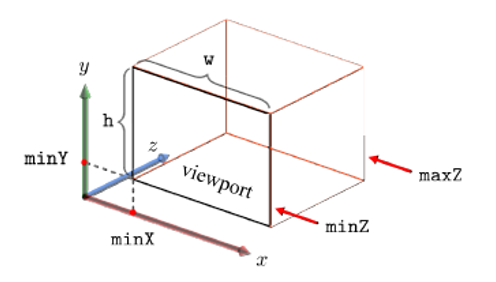
컴퓨터 스크린에 표시되는 윈도우window는 그 자신의 screen space를 가진다.
screen space는 윈도우의 왼쪽 위를 원점으로 하는 3차원 공간으로, 위의 그림에서 볼 수 있듯 screen space의 x축은 오른쪽, y축은 아래, z축은 스크린의 내부를 향한다. (Direct3D 기준)
Viewport는 이러한 screen space에 6개의 파라미터(MinX, MinY, W, H, MinZ, MaxZ)로 정의되는 3차원 영역이다.
각 파라미터의 정의는 위의 그림을 통해 쉽게 알 수 있다. w는 width, h는 height를 나타낸다.
Viewport transform은 NDC clip space를 viewport로 변환하는 작업을 지칭한다.
viewport transform은 (reflection) -> scaling -> translation의 순서로 진행된다.
반사reflection에 괄호가 쳐져 있는 이유는 필요한 경우에만 수행하는 작업이기 때문이다.
OpenGL에서는 다음과 같이 표현되는 screen space를 사용한다.
Direct3D에서의 screen space와 y축이 반전되어 있음을 볼 수 있다.
Reflection
LHS로 표현된 NDC clip space를 RHS의 screen space로 변환하는 경우를 생각해보자.
이는 아래의 NDC clip space를 위의 viewport 문단의 그림에서 표현된 좌표계로 변환하는 것과 같다.
각 좌표계의 y축이 서로 반대 방향을 향하고 있으므로 NDC clip space에
의 matrix를 곱해 y축 반전을 수행함으로 reflection이 가능하다.
y축 반전은 xz평면을 기준으로 하는 반사 변환과 같다.
이렇게 NDC clip space와 screen space의 좌표계가 다른 경우 NDC clip space에 reflection transfrom을 수행하여 좌표계를 변환할 수 있다.
Scaling
scaling matrix는 다음과 같다.
각 scaling factor는 기존의 2*2*1 크기의 NDC space를 (W, H, MaxZ-MinZ)로 변환시키기 위해 사용되었다.
Translation
translation matrix는 다음과 같다.
이 행렬을 곱함으로써 물체를 viewport의 중앙에 위치하도록 translation을 수행할 수 있다.
앞선 과정들을 통해 최종적으로 얻어지는 Viewport transform matrix는 다음과 같다.
많은 어플리케이션에서 viewport는 윈도우의 전체 영역을 차지한다.
이 경우 MinX, MinY는 원점을 가리키므로 그 값이 0이 된다.
또한 MinZ, MaxZ는 대부분 0.0과 1.0으로 설정되는데, 이를 적용하여 간소화된 viewport transform matrix는 다음과 같다.
앞선 Viewport transform은 모두 2*2*1 크기의 NDC Clip space를 바탕으로 수행되었는데, 이는 Direc3D 기반의 Viewport transform이다.
Direct3D는 2*2*1, OpenGL은 2*2*2 크기의 NDC Clip space를 사용한다.
다음은 2*2*2 크기의 NDC Clip space에 대한 view transform matrix이다.
각각 일반 형태와 간소화된 형태를 나타낸다.
Scan Conversion
Scan Conversion은 Viewport transform에 의해 screen space로 옮겨진 모든 primitive들의 내부를 채우는 프래그먼트를 생성하는 단계이다.
좁은 의미에서의 래스터화를 지칭하는 단계이기도 하다.
primitive 삼각형의 screen space에서의 픽셀 위치를 결정하고, 삼각형의 정점별 속성vertex attributes을 보간하여 이를 각 픽셀 위치에 할당한다.
정점별 속성은 어플리케이션마다 다르지만, 주로 노멀, 텍스처 좌표, 색상 등을 포함하며, 원칙적으로 모든 정점별 속성은 같은 방법으로 보간된다.
간단히 정리하자면, Scan Coversion 단계에서는 크게 다음의 두 작업을 수행한다.
1. 삼각형을 채울 screen space에서의 픽셀별 위치를 결정한다.
2. 삼각형의 픽셀별 color, depth 등의 attribute를 할당한다.
Edge Equation
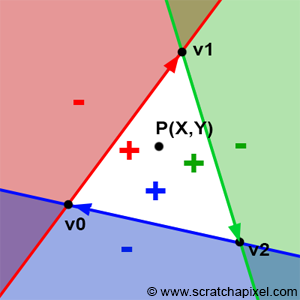
어느 한 픽셀이 특정 삼각형 내에 속하는지의 여부를 판단하기 위해 edge equation을 사용할 수 있다.
Edge Equation의 식은 다음과 같다.
어떠한 벡터와 정점에 대해 edge equation을 수행할 때,
정점과 벡터의 위치 관계에 따라 edge equation은 다음의 결과를 반환한다.
- 정점이 벡터의 왼쪽에 있을 때 : 음수
- 정점이 벡터에 속해 있을 때 : 0
- 정점이 벡터의 오른쪽에 있을 때 : 양수
위의 그림에서 볼 수 있듯, 벡터 ,,로 이루어진 삼각형 내의 정점 P는 각 edge들의 오른쪽에 위치해 있어 양수 값을 가진다.
추가로, Edge equation 식은 곧 와 로 이루어진 행렬의 determinant와 같고 이는 두 벡터가 이루는 평행사변형의 넓이와 같다.
더욱 자세한 설명은 아래의 링크를 참고한다.
https://www.scratchapixel.com/lessons/3d-basic-rendering/rasterization-practical-implementation/rasterization-stage
linear interpolation
모든 삼각형 내의 픽셀에 프래그먼트에 할당할 정점별 속성 계산을 위한 정보를 일일히 저장하는 것은 비효율적이다.
따라서 삼각형의 vertex 정보를 이용해 linear interpolation을 수행하여 정점별 속성을 구하고 이를 각 프래그먼트에 할당한다.
이에 대한 예시인 겹선형 보간Bilinear interpolation을 통해 프래그먼트의 속성을 구하는 과정을 간단하게 알아본다.
Bilinear interpolation
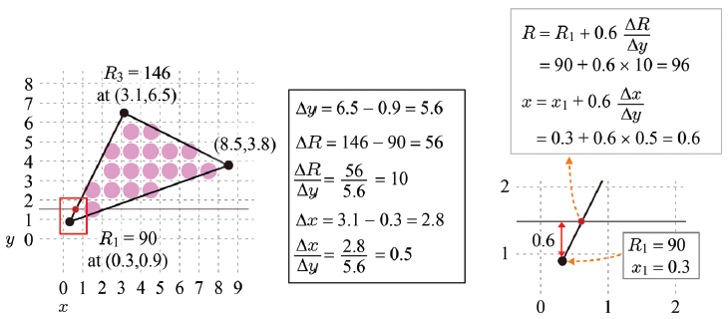
(0) 삼각형의 모든 정점에 RGB 색상 값이 계산되었다고 가정한다.
이 예시에서는 R 색상 값 속성의 보간을 다룬다.
(1) 삼각형의 각 변에 대해 여러 가지 기울기를 계산한다.
이 예시에서는 각 변의 양 끝 점의 R 색상 값, x값을 이용하여 기울기를 구한다.
( : y에 대한 R 색상 값의 기울기
: y에 대한 x의 기울기)
(2) 각 변에 대해 선형 보간을 통해 정점별 속성을 구한다.
이를 스캔 라인인 삼각형 내의 y = k들이 각 변과 교차하는 교차점에 대해 적용하여 각 교차점 별 R, x 값을 구한다.
(3) 각 변의 정점들에 대해 얻어진 R, x 값을 이용해, 스캔 라인과 x = k들의 교차점들에 대해 R, x를 구한다. ( 사용)
위의 과정에서 linear interpolation은 두 단계로 수행되었다.
(2)에서 각 변에 대한 선형 보간이 수행되었고, (3)에서 스캔라인을 따른 각 점에 대한 선형 보간이 수행되었다.
따라서 이 과정을 bilinear interpolation이라 한다.
본 예시에서는 이 과정을 통해 프래그먼트별 색상을 얻을 수 있었다.
실제 Scan Conversion 과정에서는 색상 값뿐만 아니라 노멀, 텍스처 좌표, 깊이 등 모든 정점별 속성을 보간하여 각 픽셀별 프래그먼트를 생성하게 된다. 이제 래스터화 단계가 완료되고 프래그먼트 처리 단계로 넘어가게 된다.
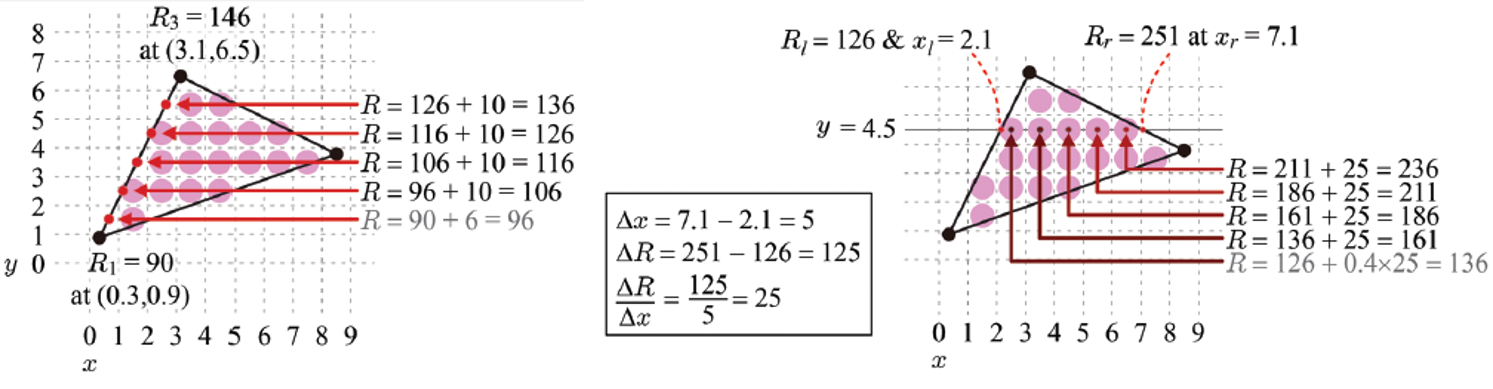
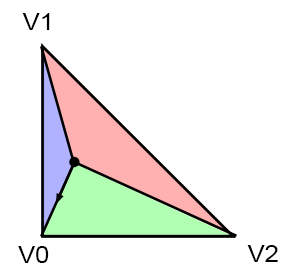
Barycentric Coordinates (무게중심 좌표계)
이러한 정점별 속성을 구하는 과정은 barycentric coordinates에서 다음과 같은 식으로 정의된다.
위 그림에서 무게중심 p에 의해 분할된 삼각형들을 마주하는 각 vertex에 따라 각각 라고 하자.
빨간 삼각형이 , 초록 삼각형이 , 파란 삼각형이 이 될 것이다.각 삼각형들의 넓이를 구하기 위해서 앞선 edge equation의 결과가 두 벡터의 determinant였고, 이는 곧 평행사변형의 넓이와 같았다는 점을 상기하자.
따라서 삼각형의 넓이는 0.5 * Edge equation이다.
이를 이용하면 이고 같은 방법으로 남은 삼각형들의 넓이 역시 구할 수 있다.은 각 삼각형들의 weight를 나타내며 이라는 조건이 있었다.
weight는 삼각형의 넓이를 전체 삼각형의 넓이로 나눔으로써 구할 수 있으므로 다음과 같은 결과를 얻을 수 있다.
이제 이렇게 구한 weight 값을 이용해 P 식에 대입하면 삼각형 내의 프래그먼트들에 대해 정점별 속성을 구할 수 있다.
Top-left Rule
Direct3D와 OpenGL에서 두 삼각형이 공유하는 변 위의 픽셀을 어떤 삼각형이 소유하는지 결정하기 위해 사용하는 규칙이다.
한 픽셀이 삼각형의 위쪽top 혹은 왼쪽left 변에 위치한 경우, 해당 픽셀은 삼각형의 소유라고 판단한다.
위 예시에서 정점 p1은 삼각형 t1의 왼쪽 변에 존재하므로 p1은 t1의 소유이다. 마찬가지로 정점 p2는 삼각형 t3의 위쪽 변에 존재하므로 p2는 t3의 소유이다.