벡터의 내적과 외적

벡터의 내적(Vector Dot Product)과 벡터의 길이(Vector length)

• 벡터의 곱을 하기 위한 두 가지 방법 중 하나는 내적(Dot Product)
• 내적은 a • b 로 표현함

• 내적은 두 벡터를 곱하여 그 결과 스칼라값을 갖게됨

• 길이(Length)는 || a || 로 표현
• 길이: 각각의 성분을 제곱하고 모두 더한 값의 제곱근과 같음

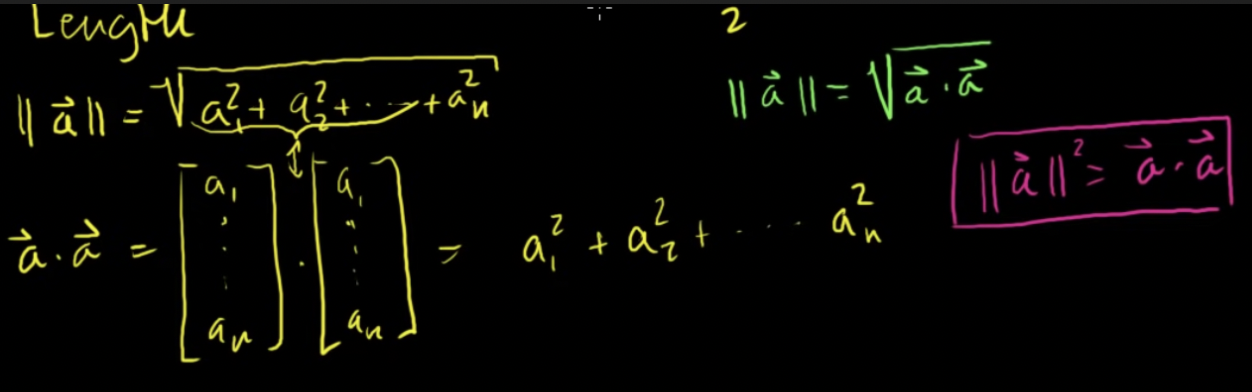
• 자기 자신과 내적: a • a → 길이의 루트 아랫부분에 있는 것과 동일
  • 스스로 내적한 값의 제곱근이 됨
  • 길이의 제곱은 벡터 a를 자신을 내적한 것과 같음

벡터 내적의 성질 증명

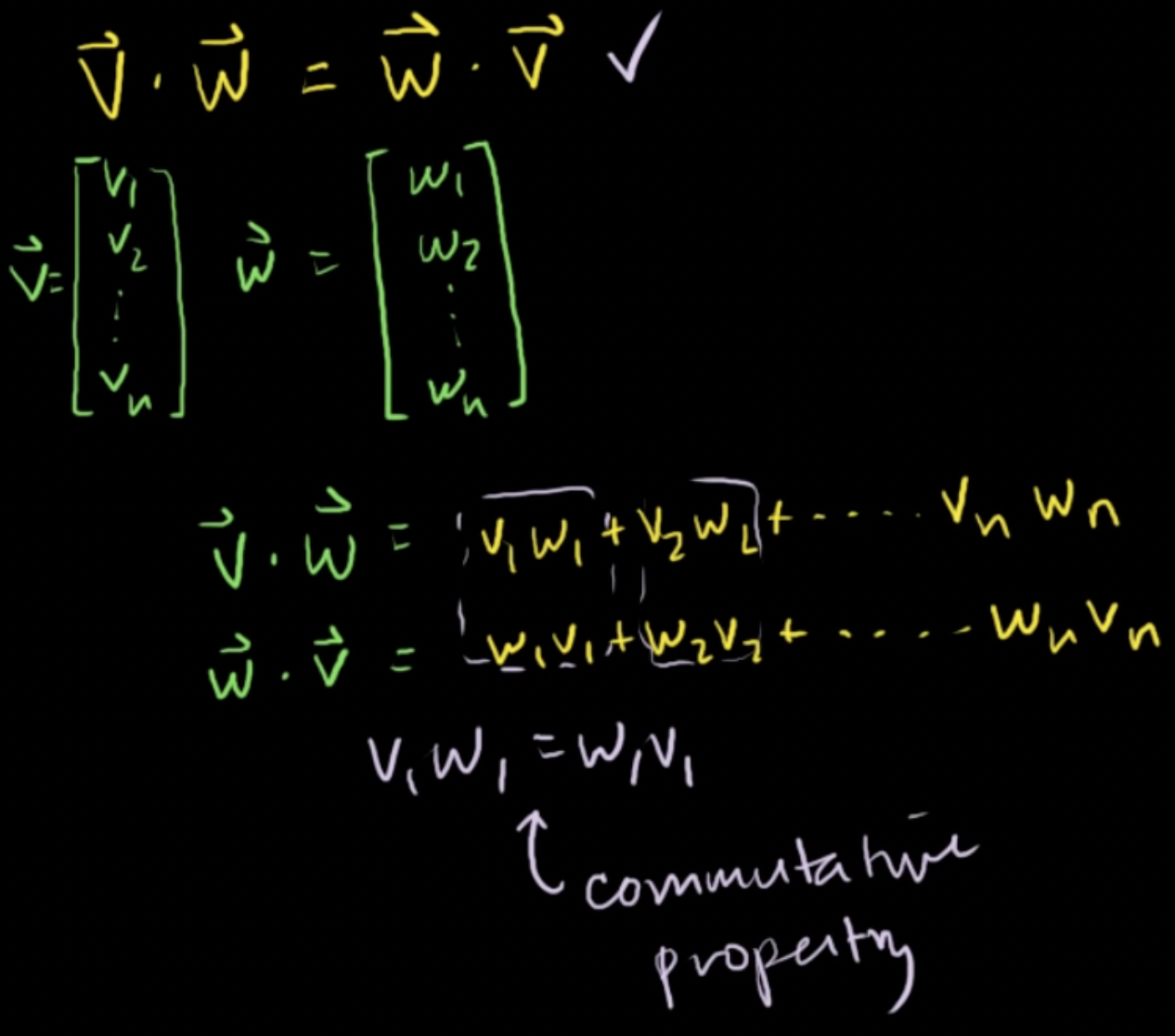
• 벡터를 내적할 때 교환법칙(commutative property)이 성립함
  • 내적할 때 순서는 상관 없음
  • v • w = w • v

• 내적에서도 분배법칙(distributive property)이 성립함
  • 벡터의 내적은 스칼라값(실수)이기에 유도 가능

• 내적에서도 결합법칙(associative property)이 성립함

  • 벡터의 내적은 스칼라값(실수)이기에 유도 가능

  → 각각에 성분에 대해서 일반적인 수에 대한 교환법칙, 분배법칙, 결합법칙이 벡터와 내적에 대해서도 비슷하게 적용 가능함

코시-슈바르츠 부등식의 증명

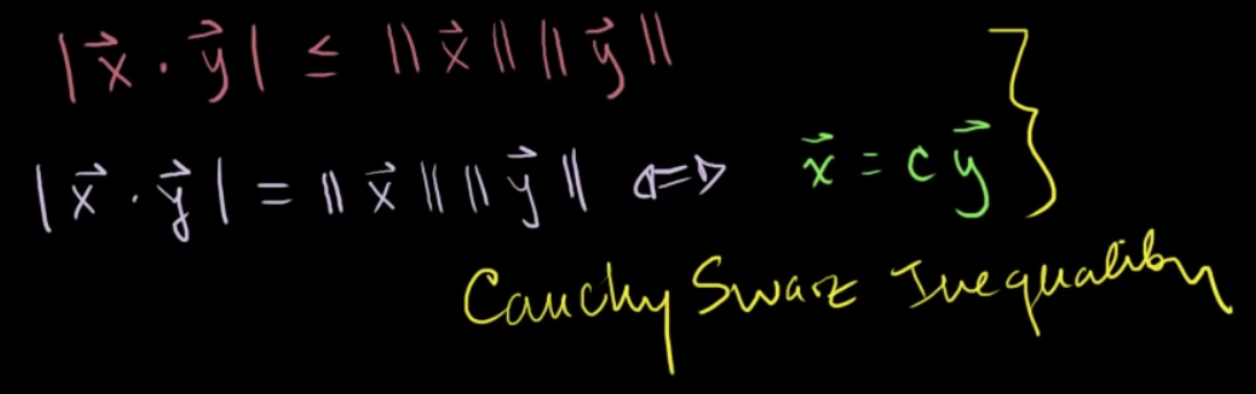
• 코시 슈바르츠 부등식 (Cauchy Swarz Inequality)
  • 두 벡터의 내적의 절댓값은 두 벡터의 길이의 곱보다 작거나 같음
  • 같은 경우는 하나의 벡터가 다른 벡터의 스칼라배인 경우
• 특정 함수를 가정해서 벡터의 길이, 분배법칙등을 활용한 수식을 통해 코시 슈바르츠 부등식 증명 가능

벡터의 삼각 부등식

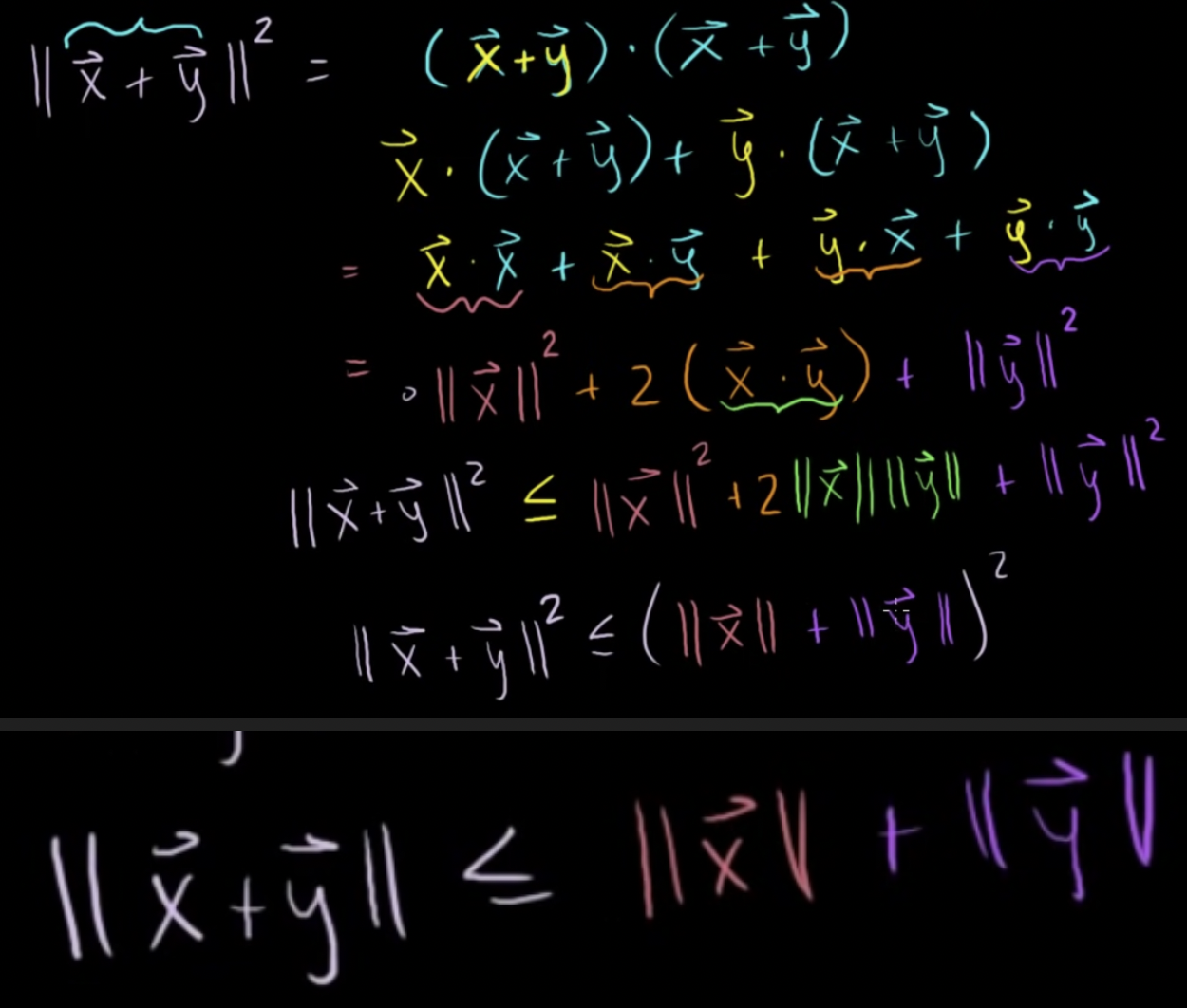
• 삼각 부등식 (triangle inequality)
  • 코시 슈바르츠 부등식과 분배법칙 등을 이용한 수식을 통해 삼각 부등식 유도 가능

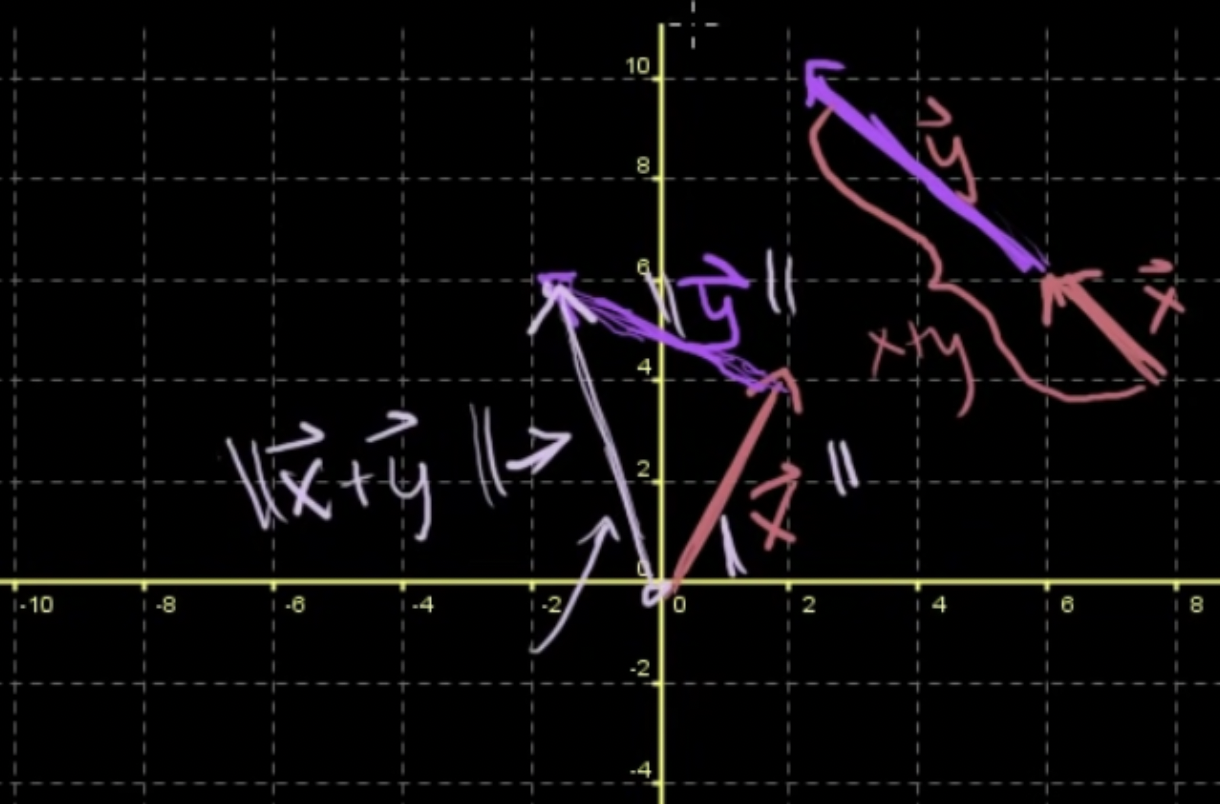
• 기하학적으로도 확인 가능
  • x와 y가 동일선상(colinear)에 있는 경우에만 x+y와 x+y가 같음

벡터 사이의 각 (angle between vectors)정의하기

• 삼각형을 만들 수 없는 경우

  

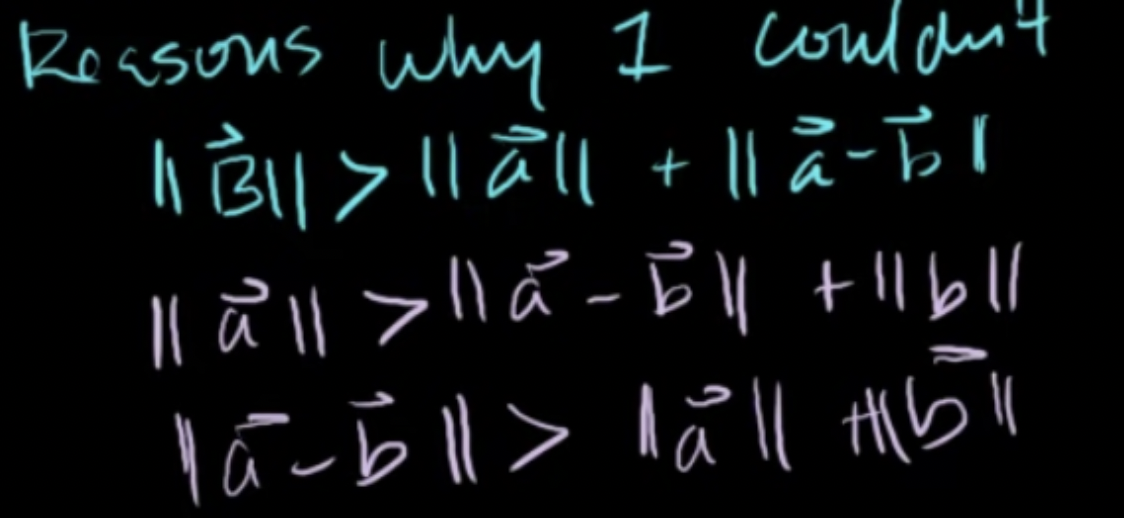
• 삼각부등식을 활용해 이를 증명할 수 있음

  

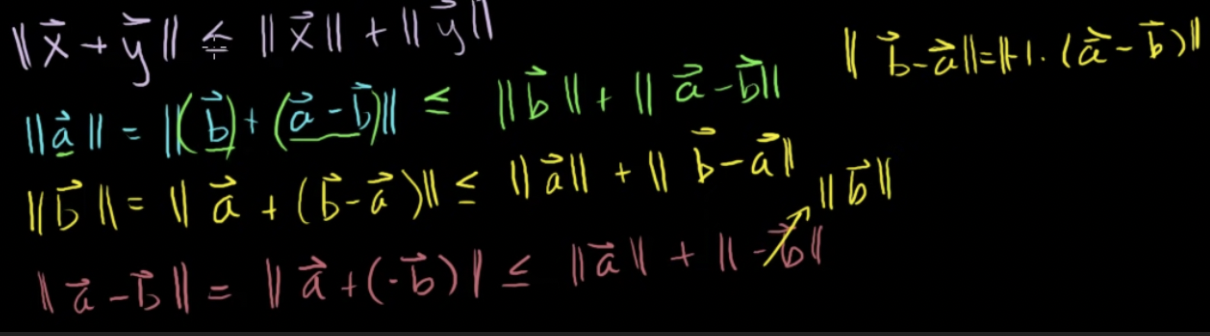
• 두 벡터 사이의 각도의 정의: 삼각형의 변 중에서 두 변은 두 벡터이고 다른 변은 두 벡터의 차

• 코사인 법칙 (law of cosines)

  

• 코사인 법칙을 활용하여 삼각형에 적용하면

  

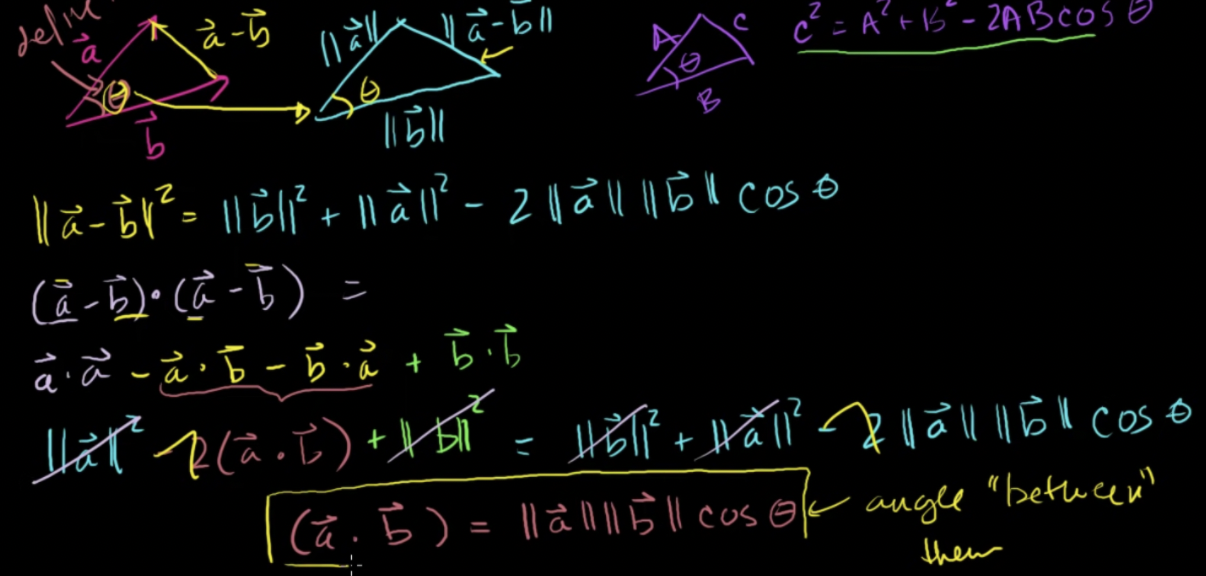
• 수직 벡터 (perpendicular vector)

  

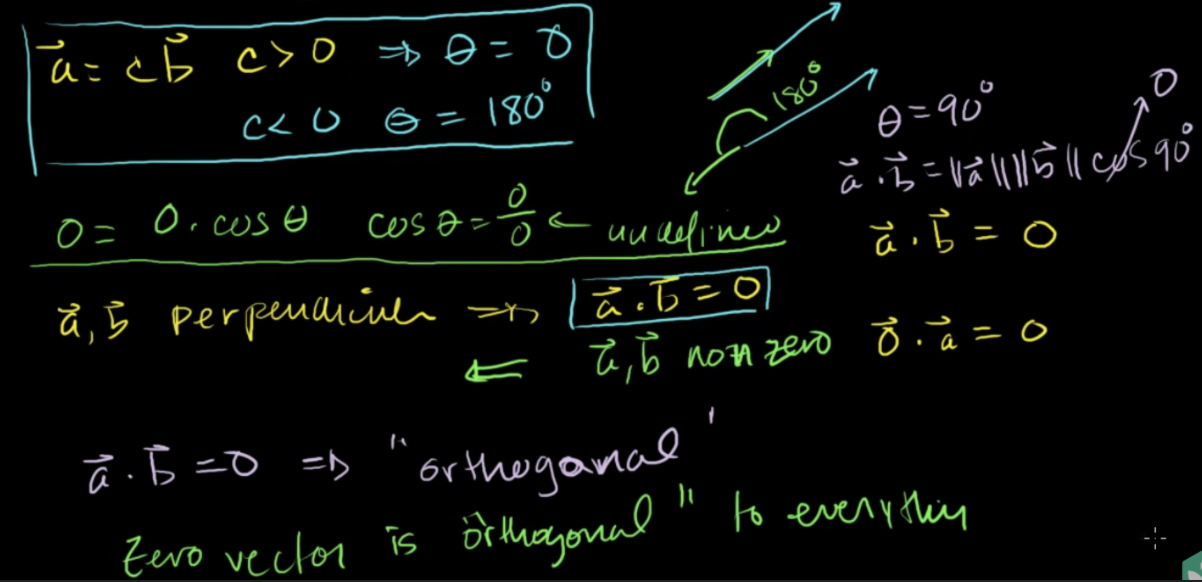
  • 두 벡터 a와 b 사이의 각도가 90도라면 수직(perpendicular)
  • a와 b가 수직이라면 내적값은 0이 됨
  • a,b가 non-zero(영벡터가 아니고), 내적값이 0이라면 a와 b는 수직
  • a • b = 0 이라는 조건이 있다면 (두 벡터의 내적값이 0이라면) 직교 (orthoganal)
    • 모든 수직인 벡터가 직교라는것을 뜻함
    • 영벡터는 모든 벡터와 직교한다는 것을 뜻함

점과 법선벡터를 이용하여 R3에서 평면 정의하기

• 3차원 공간에서의 면의 방정식 구하기
  • Ax+By+Cz = D 의 형태

• 법선벡터 (normal vector): 면에 직각(perpendicular)을 이루는 벡터 (면의 모든 것에 직각을 이룸) (perpendicular to everything on the plain)

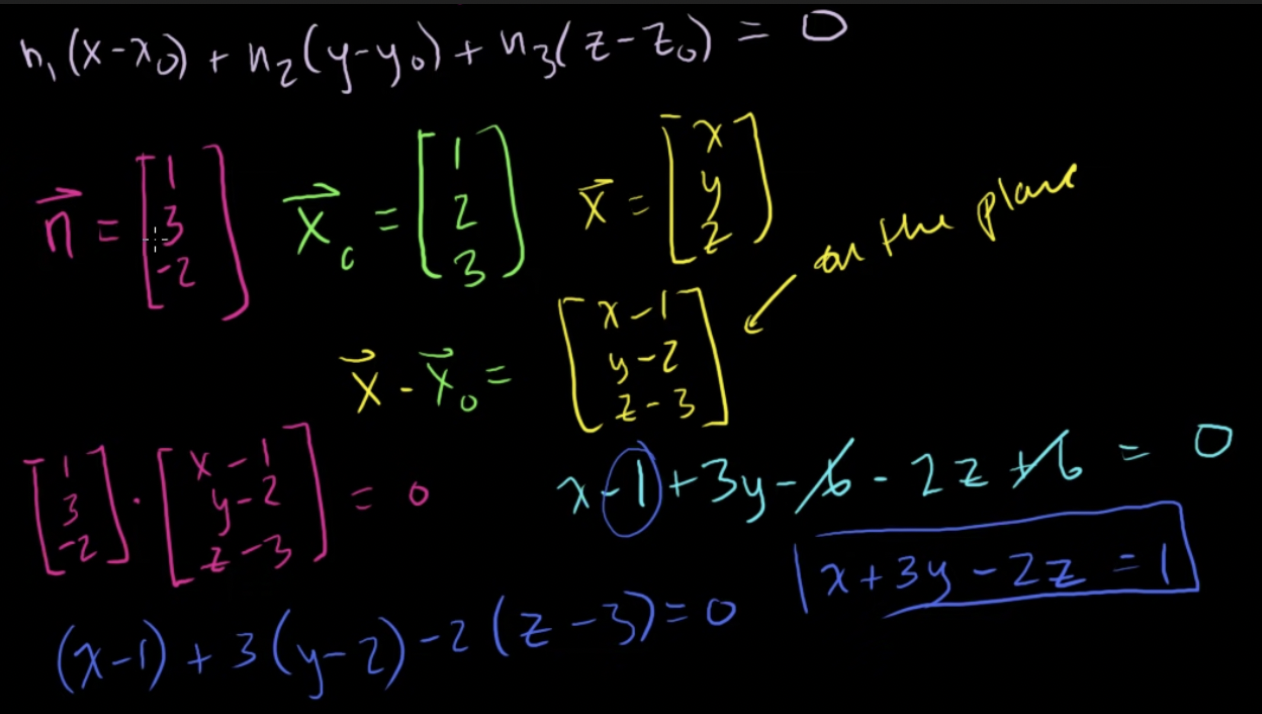
• 법선벡터는 다른 벡터와 직각을 이루어야하기에, 면 위의 임의의 점과 면 상의 벡터의 내적값이 0이어야 한다는 사실을 이용해 면의 방정식을 구할 수 있음

벡터의 외적이란?

• 벡터 곱셈에는 내적(Dot product)도 있지만 외적(Cross Product)도 있음

  • 내적은 어느차원에서든 정의되어 있는데, 외적은 R3에서만 정의되기에 한정적임
  • 내적의 결과는 스칼라이지만 외적에서는 또다른 벡터가 나옴
    • 나오는 벡터는 외적을 취할 두 벡터에 대해 모두 직교(orthogonal)함

• 외적하는 방법

  

  • 세번째 벡터가 외적을 취하는 두 벡터 a, b에 직교함 (오른손 법칙)

    

    • a와 b가 직교한다면 a와 b의 내적이 0임
    • 직교는 영벡터에도 적용됨 (수직은 영벡터x)

증명: 외적과 각의 사인값과의 관계

• 위 식에 대한 증명

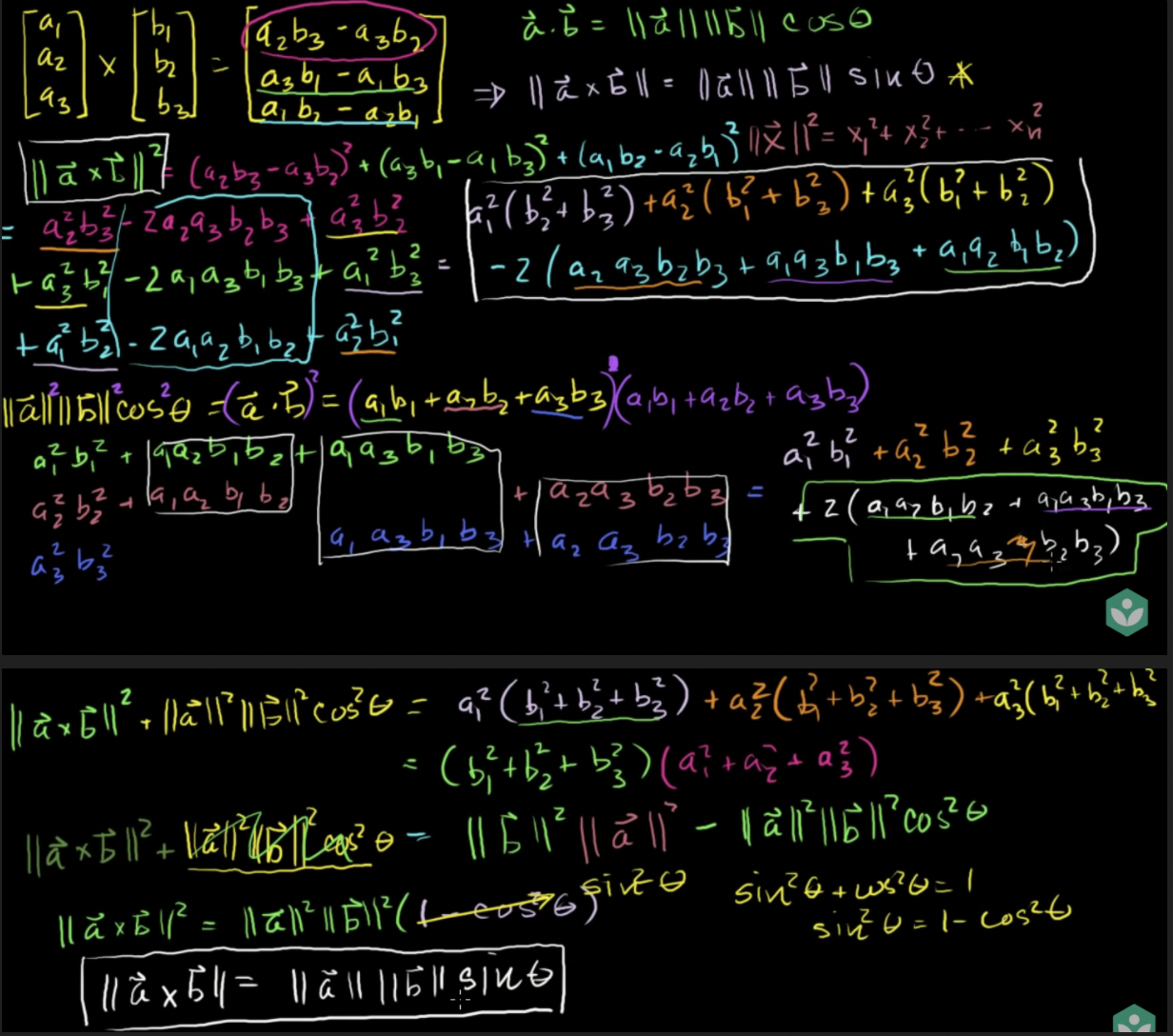
내적과 외적의 비교 / 직관

• 두 벡터가 있을 때 사이각 구하기 - 내적과 외적을 이용

  

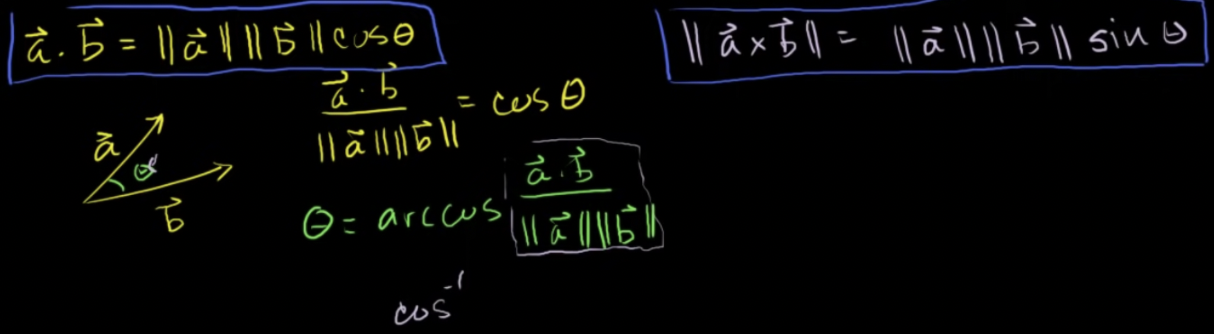
  • 내적

    

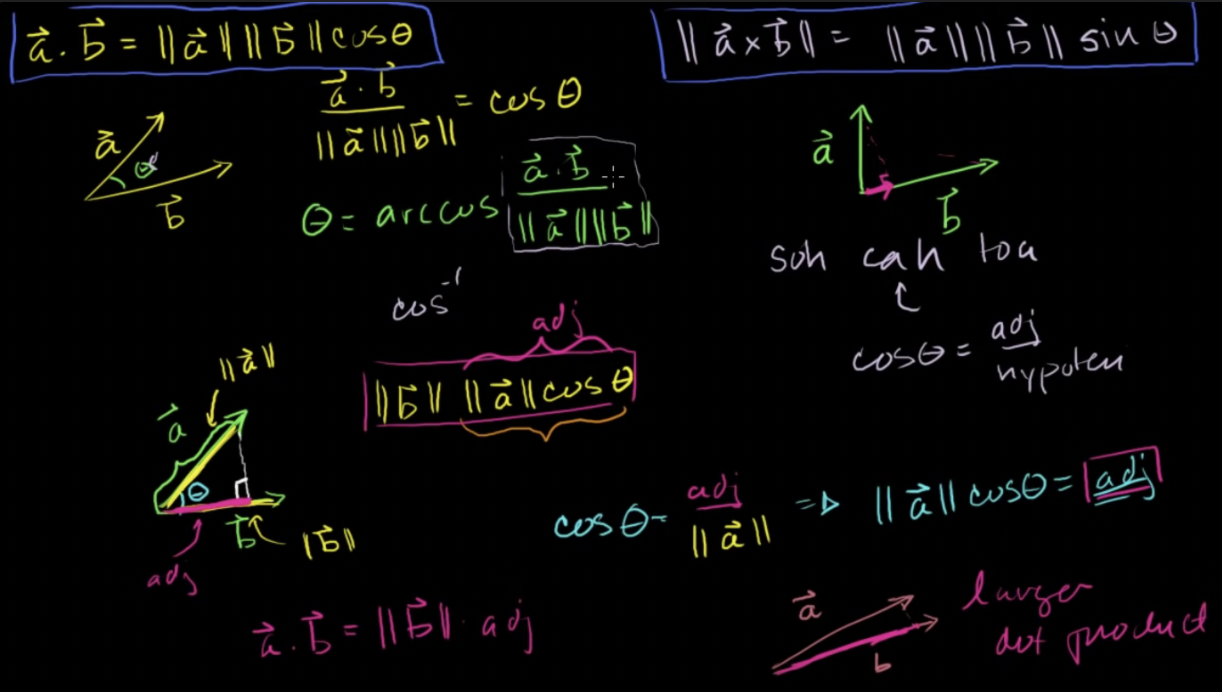
  • 내적은 얼마나 두 벡터가 같은 방향으로 향하고 있는지를 말해줌

  • 외적

    

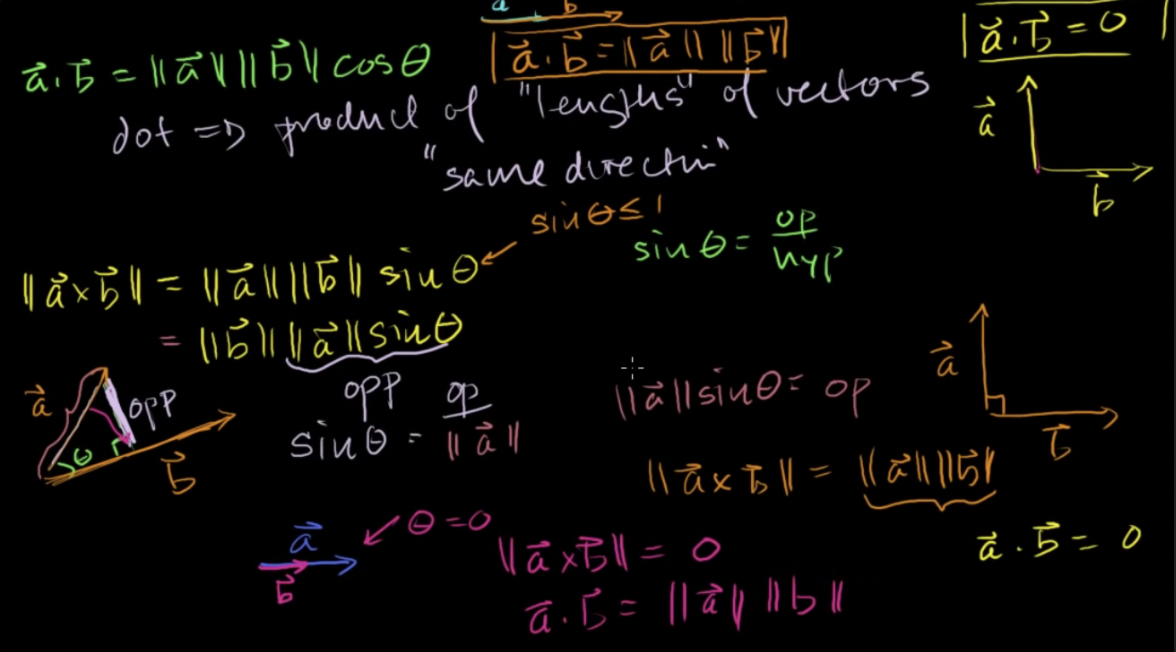
• 외적을 이용해 평행사변형의 넓이 구하기

  

벡터의 삼중적의 확장

• 삼중곱(triple product): 벡터 3개의 외적

  • 벡터를 단위벡터와 곱한것으로 표현해내고, 외적하고 식을 풀어냄
  • 결과: 괄호안의 첫번째 벡터를 나머지 두 벡터의 내적과 곱하고, 괄호안의 두번째 벡터를 나머지 두 벡터의 내적과 곱한것을 빼줌

평면방정식의 법선 벡터

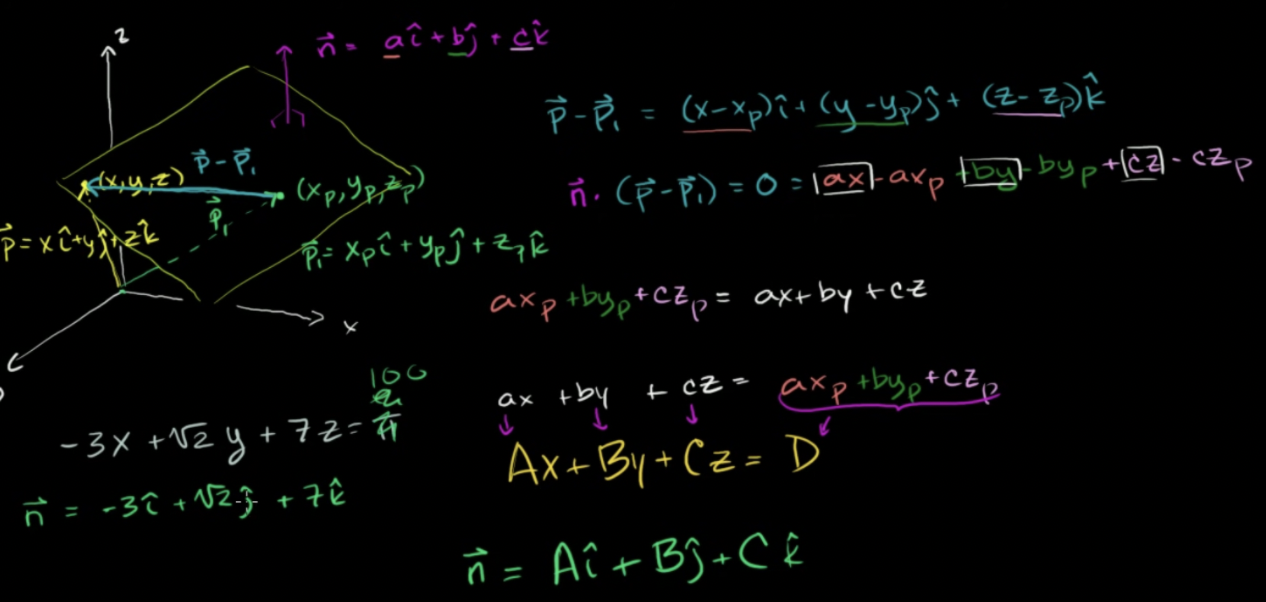
• 면에 관한 방정식이 주어졌을 때 법선 벡터를 구하는 방법
  • 법선벡터는 면에 수직하므로 면위의 직선(벡터n)과 내적하면 0
  • 법선벡터는 면의 방정식의 계수들을 뽑아내어 단위벡터로 구성하면 됨
  • D는 신경안써도 됨: d부분이 면을 이동시키긴 해도 면이 기울어진 정도에는 영향을 주지 않기 때문

점과 평면 사이의 거리

• 평면상에 있지 않은 점과 평면사이의 거리 구하기

  

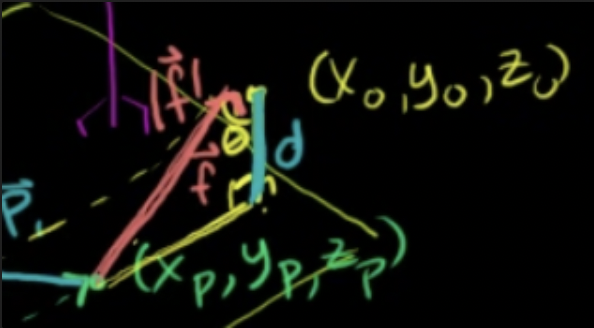
  • 점에서 평면까지 수직으로 내린 길이 구하기: 빗변의 길이와 각도 활용

평면 사이의 거리

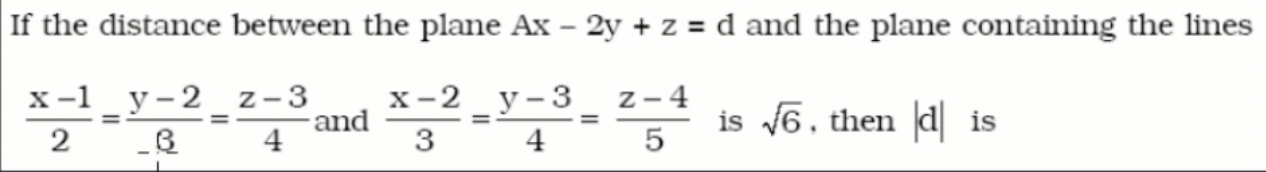
• 평면 Ax-2y+z=d와 다음 직선들을 포함하는 평면 사이의 거리가 루트6이면 d의 절댓값은? → 평면과 평면 사이의 거리에 대한 이야기, 한 평면은 직선 2개 포함
• 평면 사이는 평행함, 평행하지 않다면 거리가 루트6이 아니라 0이기 때문

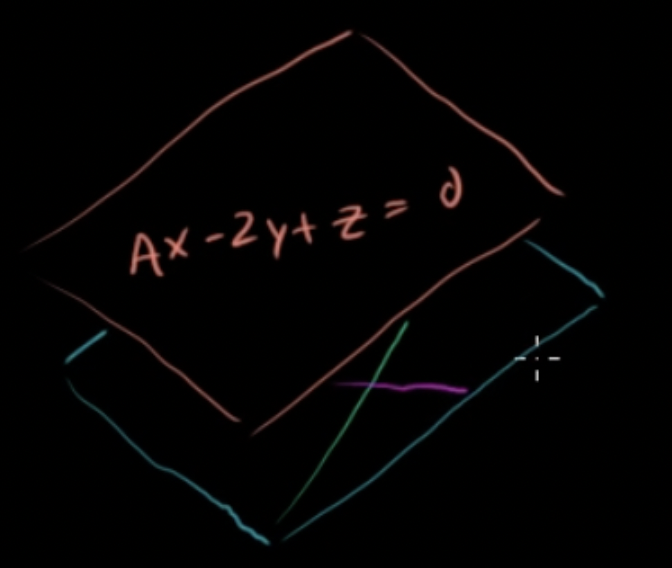
• 먼져 파란 평면의 방정식을 구하해야함

  • 파란 평면의 방정식은 주황 평면의 방정식과 닮았을 것이므로, a의 값을 구해야함

  • 그러기 위해 파란 평면 위의 한 점을 찾고 그 점에서 주황 평면까지의 거리를 구함

  • 파란 평면위의 두 벡터를 구하고 두 벡터를 외적하여 평면에서의 법선을 구함

    

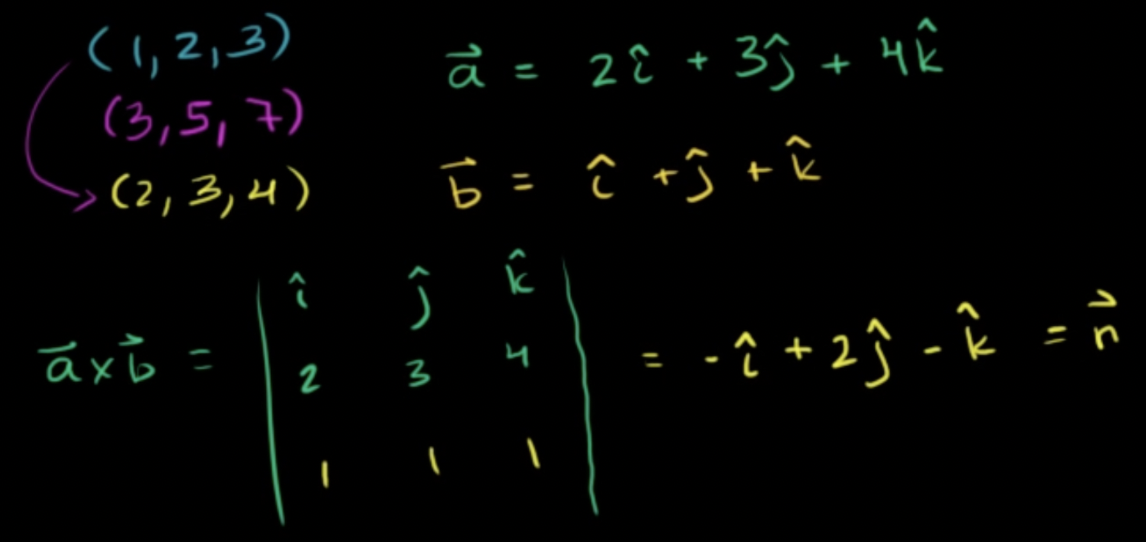
  • 평면의 법선 벡터와 임의의 x,y,z에 대하여 대응하는 임의의 벡터를 내적

    

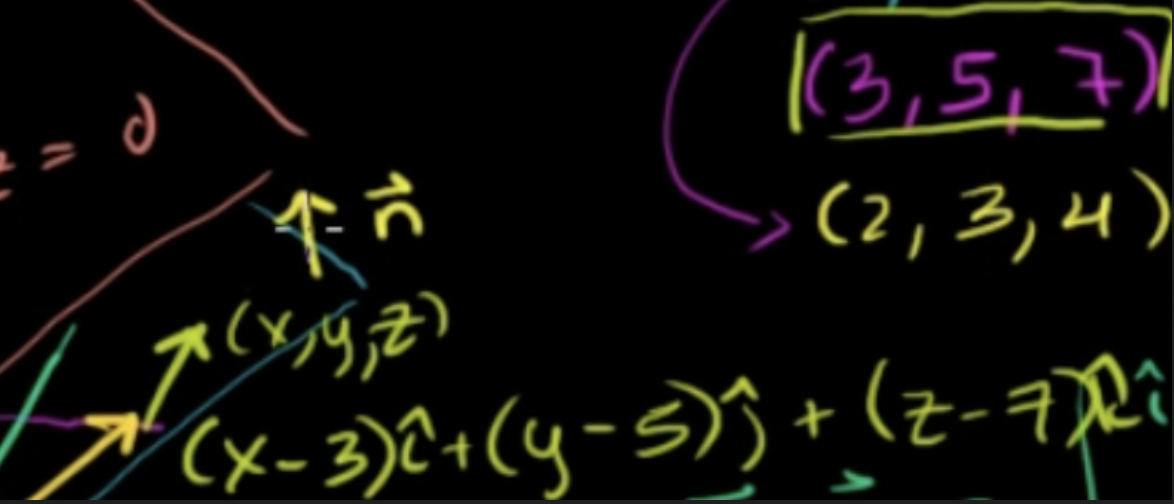
    • 이 벡터와 법선벡터를 내적하면 0 (벡터가 평면위에 있기 때문)
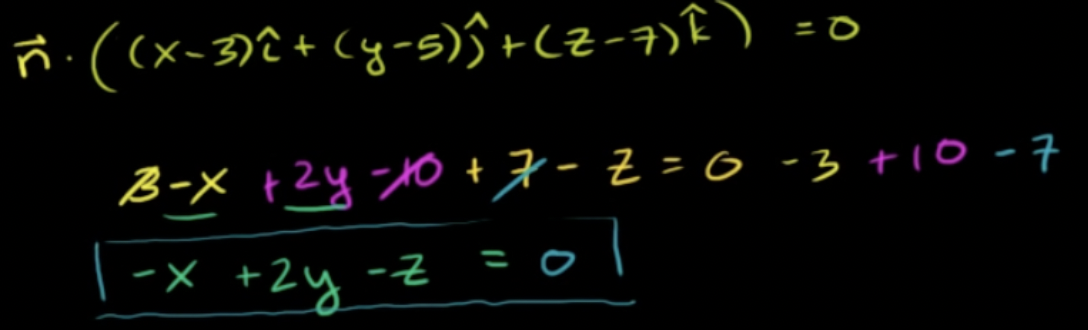
    • 파란 명면의 방정식: -x + 2y - z = 0, 혹은 x-2y+z = 0

• 파란 평면과 주황 평면은 평행하므로 x,y,z항의 계수의 비율은 동일해야 함

• 이제 두 평면 사이의 실제 거리를 구할 수 있음

  • 파란 평면위의 점과 주황 평면 사이의 거리를 구함 (점과 평면 사이의 거리 구하는 공식 이용)

    

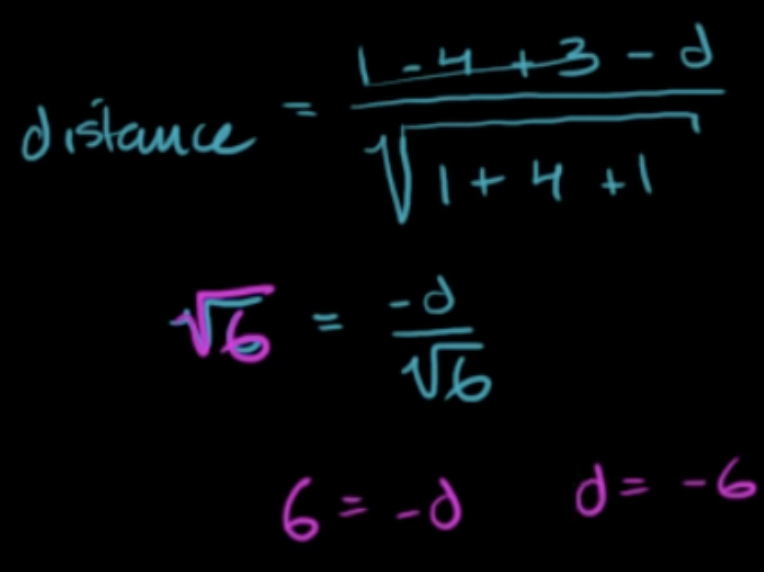
    • 따라서 최종적으로 구하고자하는 |d| 는 6
    • 파란 평면 위의 한 점과 이 점에서 가장 가까운 주황 평면에서의 한 점 사이의 거리는 6

참고 [칸아카데미] 모두를 위한 선형대수학