부분공간과 부분공간의 기저

선형 부분공간 (linear subspaces)

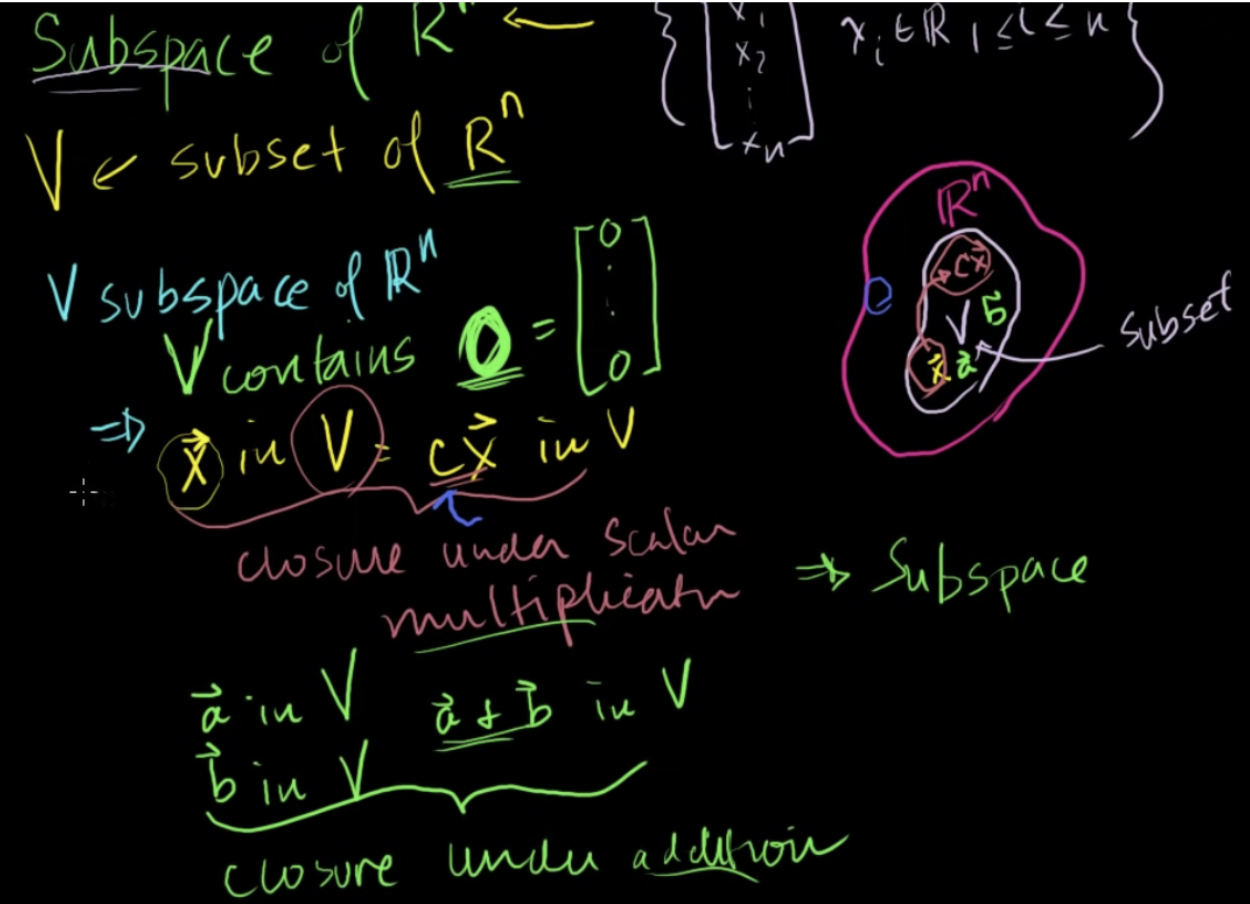
• V가 Rn의 선형 부분공간(linear subspace)라는 것은 3가지를 의미함
  1. V가 영벡터를 포함
  2. x가 V에 포함된 벡터라면 x에 임의의 스칼라를 곱한 값(cx)또한 V에 있음 (닫혀있음, closure)
     • 만약 집합의 임의의 원소를 가지고있다면 곱셈에 대해 닫혀있는 것
     • 스칼라 곱셈에 대해 갇혀있음 (closure under scalar multiplication)
     • 집합에서 어떤 원소를 다른 스칼라와 곱하더라도 그 값은 집합에 여전히 있을 것
     • 만약 어떤 스칼라랑 곱했는데 집합에서 벗어나게 된다면 (부분집합에 없는 다른 벡터가 나오게 된다면) 이 부분집합은 부분공간이 아니게 됨
     • 부분집합에 있는 임의의 벡터에 어떤 실수 스칼라를 곱하더라도 부분집합에 있는 또다른 원소를 얻어야 함
  3. 두 벡터 a, b가 집합 V에 있다면 V가 Rn의 부분공간이라면 a+b가 무조건 V에 있음
     • 집합은 덧셈에 대해 닫혀있음 (closure under addition)
     • 집합의 두 벡터를 더하면 집합 내의 또다른 벡터가 나옴

→ 영벡터를 포함하는 Rn안의 어떤 벡터들의 집합을 가지고 있다면, 그리고 곱셈과 덧셈에 대해 닫혀있다면 부분공간이 존재함 (부분공간의 정의)

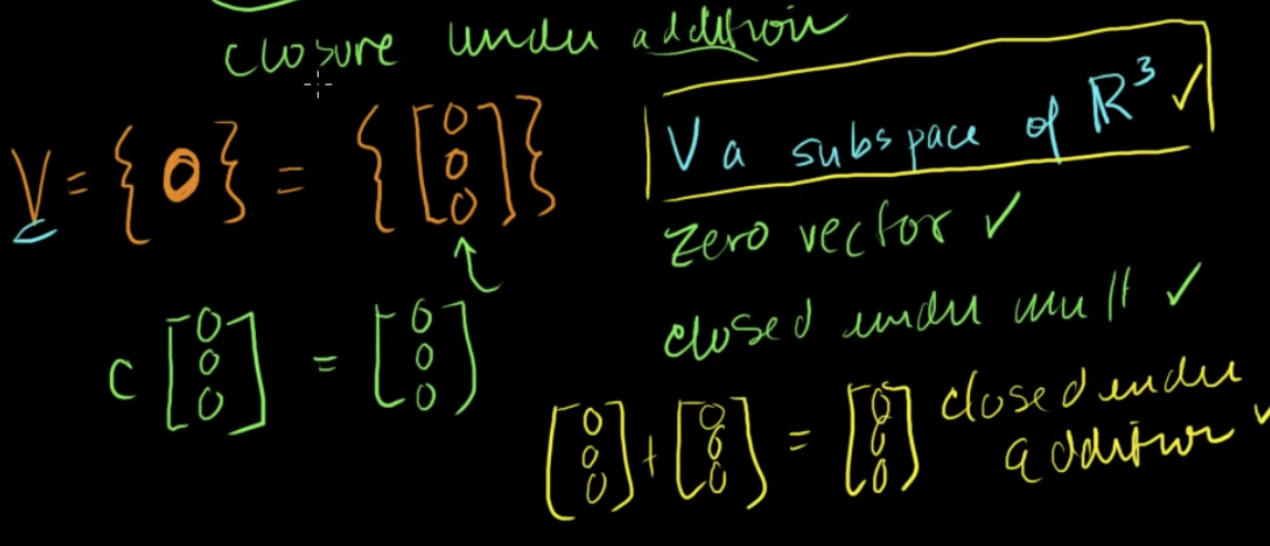
• 벡터 집합에 오직 한 개의 벡터, 영벡터만 있다고 할 때 집합 V는 R3의 부분공간일까? → 3가지 조건 만족해야함

  1. 영벡터 포함 (o)

  2. 곱해도 같으니 곱셈에 대해 갇혀있음 (o)

  3. 더해도 같으니 덧셈에 대해 갇혀있음 (o)

     → R3의 부분공간임

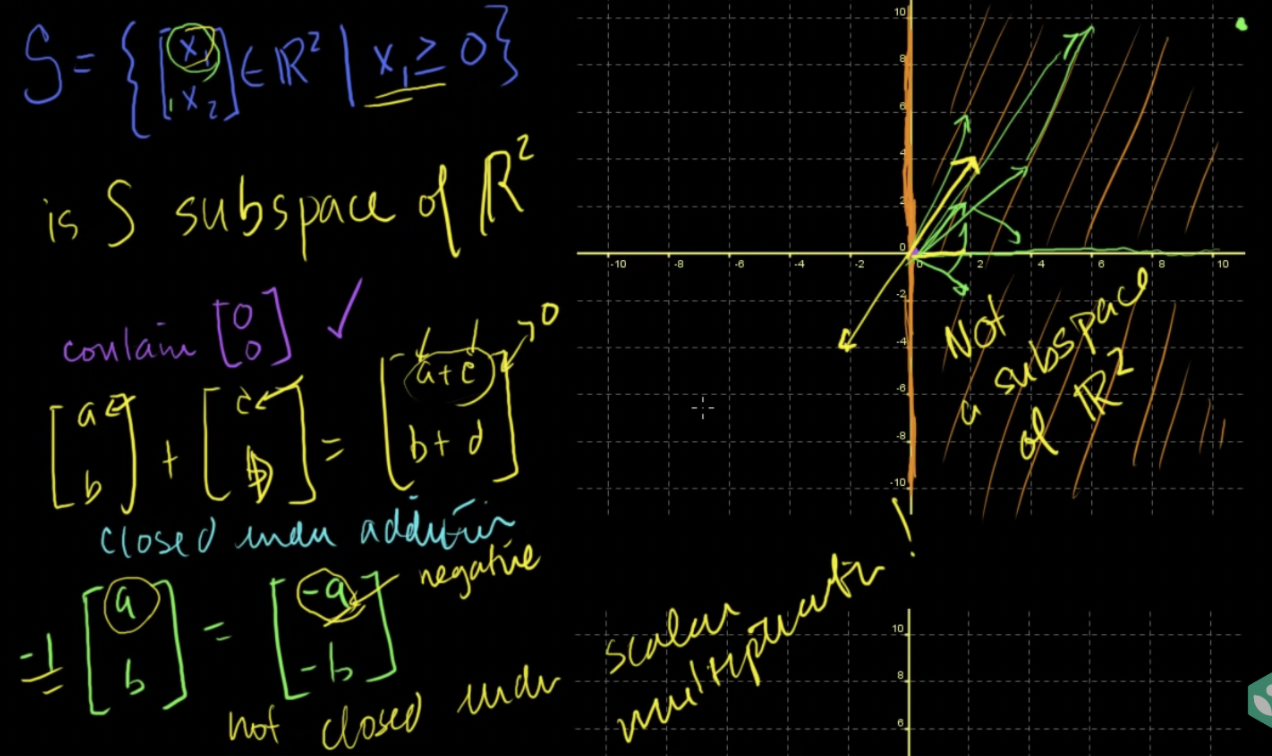
• 첫번째 항이 최소 0이상인 모든 R2의 벡터를 가진 집합 S가 있을 때 S가 R2의 부분공간일까?
  1. 0,0 포함 (o)
  2. 덧셈에 대해 닫혀있음 (o)
  3. -1을 곱하면 영역 밖으로 빠져나옴, 양의 값에 -1을 곱하면 음의 값이 됨 (x),스칼라 곱셈에 대해 닫혀있지 않음(x)

→ R2의 부분공간이 아님

• v1, v2, v3의 생성이 Rn의 유효한 부분공간일까?

  

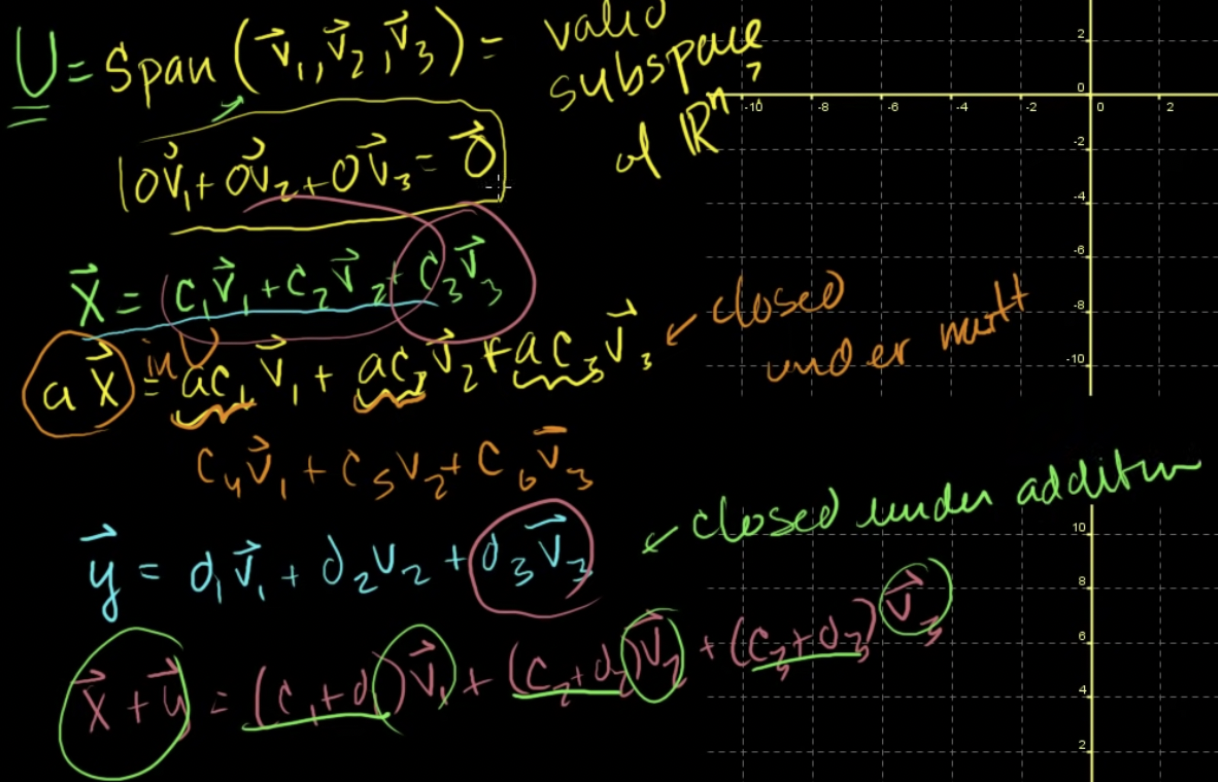
  1. 각각에 0을 곱하면 영벡터 (o)

  2. 곱셈에 대해 닫혀있음 (o)

     

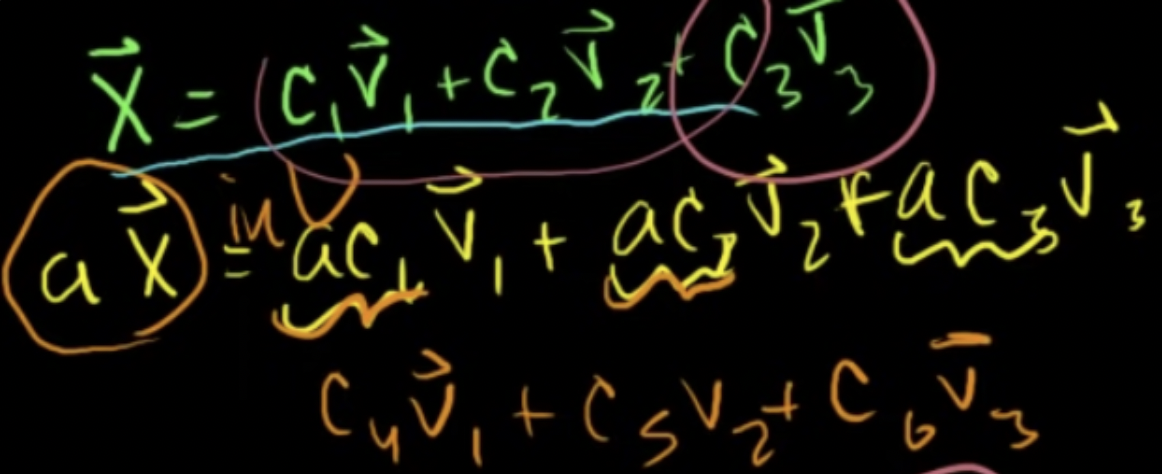
  3. 덧셈에 대해 갇혀있음 (o)

     

→ 유효한 부분공간임

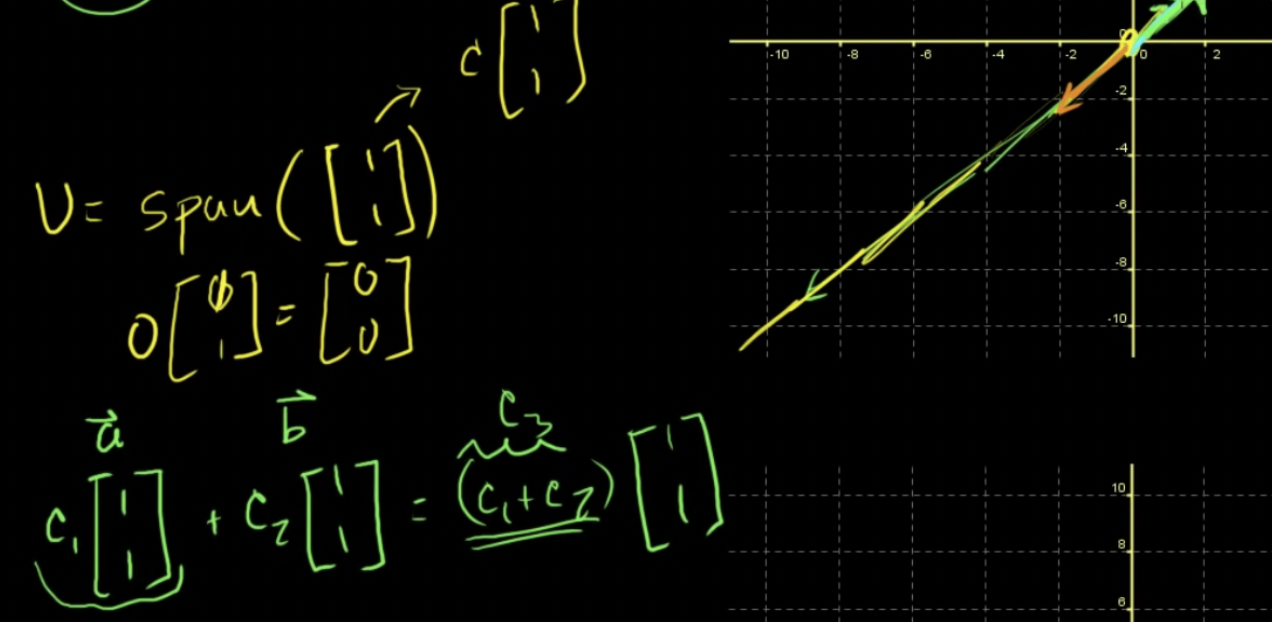
• 표준위치에서의 벡터 (1,1)의 생성은 이 벡터의 모든 선형결합
  • 0,0 포함
  • c에 대해 (1,1)에 곱하면 무엇을 곱하든 생성안에 있는 것과 같은 것
  • 덧셈 또한 선형생성안에 있음

→ 유효한 부분공간

부분공간의 기저 (basis of subspace)

• 생성(span): 부분공간이 벡터들로 만들 수 있는 모든 가능한 선형결합의 집합을 말함, 결합의 모든 경우의 수를 벡터의 집합으로 만듦
• 선형독립: c1v1 + c2v2 +…+ cnvn = 0벡터 에서 c1,c2,…,cn이 모두 0이어야만 하는 경우, 어느 벡터도 나머지 벡터의 결합으로 표현될 수 없음
• 이 벡터집합의 생성이 부분공간V와 같거나 이 부분공간V을 생성하고, 동시에 모든 벡터가 선형독립일 때 이 집합을 S라고 정의
• 벡터집합 S가 부분공간 V의 기저 (S is a basis for V)
  • 어떠한 집합의 기저라는 것은 이 벡터들이 부분공간을 생성하고 부분공간의 어떠한 벡터도 될 수 있으며 그 벡터들은 선형독립이라는 것
• 기저
  1. 이 벡터들이 부분공간을 생성한다는 것 (이 벡터들의 생성이 부분공간이라는 것)
  2. 이 백터들이 선형독립이라는 것
• 기저는 최소한의 벡터집합
  • 어떠한 공간을 생성하는데 필요한 최소한의 벡터집합(minimum set of vectors that spans the subspace)

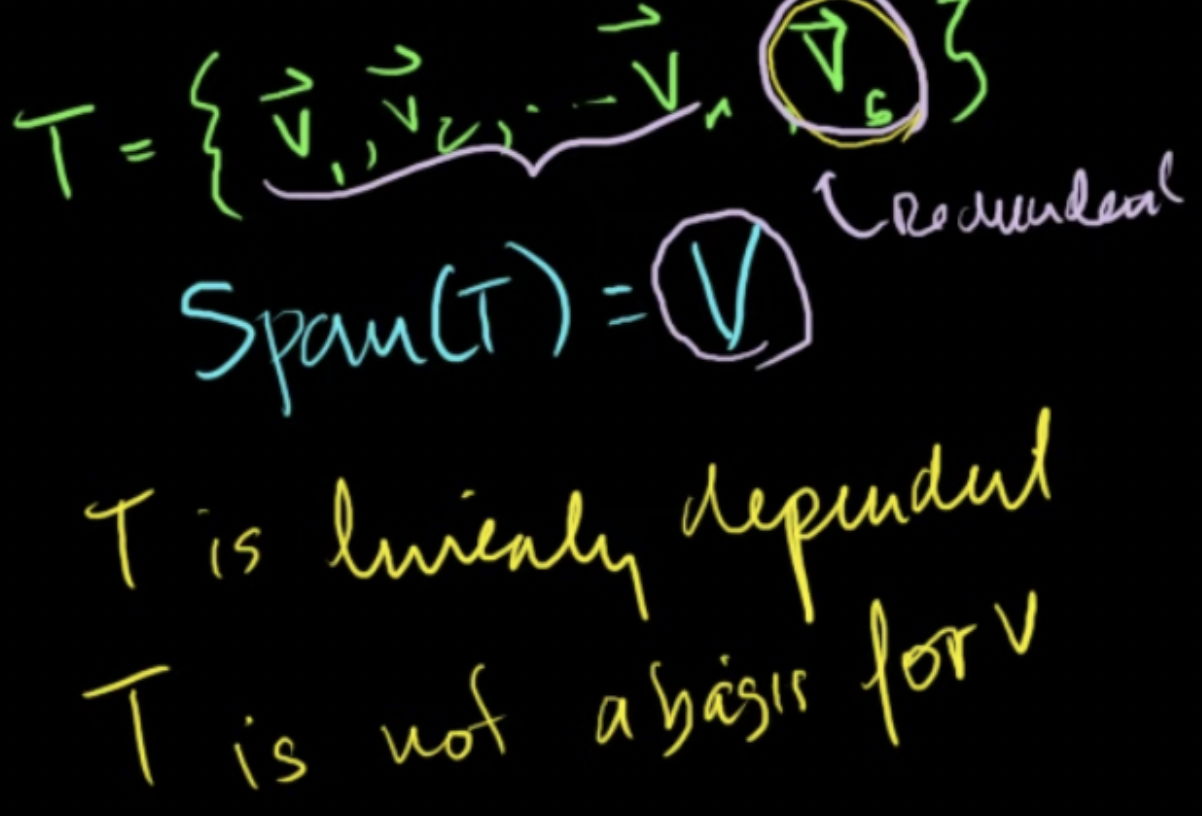
• V에 v1+v2인 vs 벡터가 추가된 T가 있다고 했을 때 T는 부분공간을 생성할 수는 있으나 마지막 벡터가 없어도 똑같은 부분공간을 생성할 수 있기 때문에 최소한의 집합은 아님

  • T는 V의 기저라고 할 수 없음
  • T는 선형종속
  • vs는 불필요함, 기저에는 불필요한 중복이 존재하지 않음

• 부분공간이 존재한다고 해서 그 기저가 하나만 있는 것은 아님, 여러 개의 기저가 존재할 수 있음, 보통 하나의 부분공간에 무한개의 기저가 존재함

• 표준 기저 집합(Standard basis): 단위벡터 i(1,0)와 단위벡터 j(0,1)로 구성된 집합

  • 이 단위벡터들은 데라크르트 좌표의 표준 기저
  • 표준 기저 집합 벡터의 조합을 이용하여 부분공간 내의 어떤 벡터라도 표현할 수 있음

• 어떠한 부분공간의 기저가 있다면 그 부분공간은 그 기저 벡터들의 유일한 결합으로 표현됨

• 기저집합이라하면 R2를 생성하는 최소한의 벡터들의 집합이어야 함

참고 [칸아카데미] 모두를 위한 선형대수학