Abstract

  Coarse voxels / point cloud 등의 user guide를 통해 high-resolution 3D shapes를 합성해내는 deep 3D conditional generative model, DMTet (MT in a DL framework) 제안. Discretized signed distance function을 encoding하는 deformable tetrahedral grid와 이러한 implicit signed distance representation을 explicit surface mesh representation으로 변환하는 differentiable marching tetrahedra layer로 구성.

---

1. Introduction

• 비전문가는 voxel 등을 통해 3D shape를 구현하곤 하며, 이러한 coarse & voxelized objects를 고화질로 upscale 해주는 AI tool의 수요 발생. Learning-based 3D content creation framework의 학습을 위해서도 효과적인 3D representation이 필요.

• 빠른 inference 속도를 위한 효율적인 메모리 관리 및 연산을 통해 local geometric details까지 잡아내야 함.

• 하지만 이전까지의 neural implicit representations 방법론은 SDF(signed distance field)나 OF(occupancy field) 값들에 대한 regression으로 학습되어 target surface에 대한 explicit supervision을 활용하지 못함.

• Underlying surface를 deformable tetrahedral grid로 implicit하게 encoding한 뒤, Marching Tetrahedra (MT) algorithm으로 explicit mesh로 변환.

---

2. Related Work

Voxel-based Methods

• 초반엔 convolutional neural network로 regular grid에 대한 voxel로 나타내도록 학습 시도(e.g. DECOR-GAN).

• Resolution에 따라 기하급수적으로 증가하는 연산량 및 메모리 $\rarr$ Octrees로 해결하려는 시도.

  $\Rarr$ Grid 변형(deformation)과 분할(subdivision)을 동시에 수행하는 hierarchical deformable tetrahedral grid 제안.

Deep Implicit Fields (DIFs)

• 3D shape를 neural network로 parameterize.

• DIF-based shape synthesis approaches는 학습 시 추출된 3D location에 의존도가 높고 mesh로 변환 시 Marching Tetrahedra 등의 iso-surfacing step이 연산량이 높다는 문제점 발생.

  $\Rarr$ DMTet의 경우 iso-surfacing formulation이 미분가능하여 end-to-end 학습을 가능케 함.

Surface-based Methods

• DefTet에서 grid vertex coordinates와 occupancy values가 학습되는 deformable tetrahedral grid를 제안했으나 grid resolution에 따라 연산량이 크게 증가하고, occupancy loss와 surface loss가 joint하게 학습되지 않음.

---

3. Deep Marching Tetrahedra

• DefTet에서와 같이, deformable tetrahedral grid로 encoding된 sign distance field(SDF) 사용.

• DefTet은 각 tetrahedron에 대한 occupancy를 encoding했다면, DMTet은 grid의 각 꼭짓점에 대한 signed distance values를 encoding. 또한 predicted surface에 대해 tetrahedra를 선택적으로 분할하여 메모리 및 연산량 감소.

• 이렇게 생성된 signed distance-based implicit representation은 marching tetrahedra layer를 통해 triangular mesh로 변환된 후, differentiable surface subdivision module을 통해 parameterized surface로 변환.

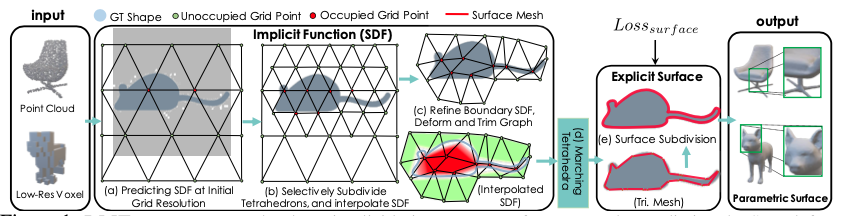
3.1.1 Deformable Tetrahedral Mesh as an Approximation of an Implicit Function

• Deformable tetrahedral grid $(V_T, T)$. $V_T$는 grid $T$의 모든 꼭짓점 집합. $T$는 네 꼭짓점 좌표 $\{v_{a_k}, v_{b_k}, v_{c_k}, v_{d_k}\}$로 표현되는 tetrahedron $T_k$로 구성. Sign distance field는 각 꼭짓점의 값들을 interpolate하여 구함.

3.1.2 Volume Subdivision

• 단일 tetrahedron이 서로 다른 SDF 부호를 갖는 경우 이웃 tetrahedron까지 surface tetrahedra $T_\text{surf}$로 구분하여 각 변의 중점을 추가(해당 변에서의 SDF 평균값 부여), resolution을 높여나감.

3.1.3 Marching Tetrahedra for converting between an Implicit and Explicit Representation

• Encoded signed distance field는 tetrahedron의 변을 따라 interpolate하였을 때 zero crossings를 연결하여 구성(Marching Tetrahedra algorithm)

  

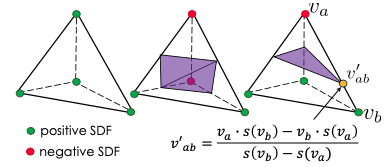
3.1.4 Surface Subdivision

• 생성된 surface mesh는 differentiable surface subdivision module로 quality를 향상시킬 수 있음. Loop Subdivision methodd를 적용하되, parameter(mesh vertex $v_i'$과 이들 간 smoothness를 결정하는 $\alpha_i$)가 함께 학습될 수 있도록 변경.

3.2 DMTet: 3D Deep Conditional Generative Model

• Point cloud + coarse voxelized shape $-$(DMTet)$\rarr$ High resolution 3D mesh

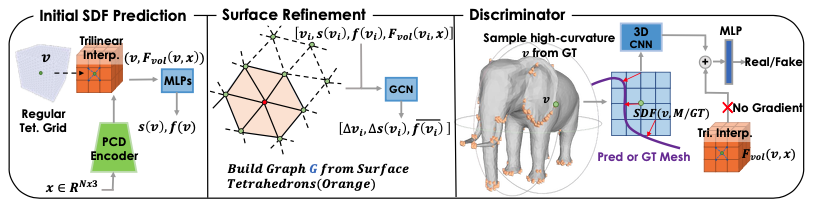
3.2.1 3D Generator

Input Encoder

• Point cloud(coarse voxelized shape가 입력될 경우 표면으로부터 points sampling)로부터는 PVCNN encoder로 3D feature volume $F_\text{vol}(x)$ 추출.

• Grid vertex $v$에 대해, trilinear interpolation을 통해 $F_\text{vol}(v, x)$ 계산.

Initial Prediction of SDF

• PVCNN encoder로 얻어진 grid vertex $v$의 feature $F_\text{vol}(v, x)$와 $v$의 좌표로부터 SDF $s(v)$를 출력하는 MLP 학습: $s(v)=MLP(F_\text{vol}(v, x), v)$. 추가적으로, surface refinement에 쓰일 feature vector $f(v)$도 출력.

Surface Refinement with Volume Subdivision

• SDF $s(v)$를 통해 surface tetrahedra $T_\text{surf}$와 이의 꼭짓점과 변으로 구성된 graph $G=(V_\text{surf}, E_\text{surf})$ 구성.

• GCN을 통해 각 꼭짓점 $i$에 대한 position offset $\Delta v_i$과 SDF residual value $\Delta s(v_i)$, updated per-vertex feature $\overline{f(v_i)}$ 예측.

Learnable Surface Subdivision

• 최종적으로 출력된 surface mesh에 대해, GCN을 적용해 각 꼭짓점에 대한 updated position $v_i'$와 Loop Subdivision을 위한 $\alpha_i$ 계산.

요약하자면,
1) Point cloud 혹은 coarse voxelized shape로 입력된 3D shape로부터,
2) PVCNN encoder로 tetrahedral grid에 대한 feature volume을 계산한 뒤,
3) MLP로 해당 grid에 대한 SDF 값과 refinement를 위한 additional feature 계산.
4) 이로부터 surface tetrahedra를 구분하여 graph를 구성하고,
4) GCN으로 grid 좌표와 SDF 값에 대한 offset을 계산하여 update한 뒤,
5) Surface tetrahedra에 한해 volume subdivision step과 additional surface refinement step을 거침.

3.2.2 3D Discriminator

• Generator가 예측한 최종 surface를 SDF로 변한한 뒤, DECOR-GAN의 3D CNN을 real vs. generated shape를 구분하는 3D discriminator $D$로서 활용.

3.3 Loss function

• Surface alignment loss + Adversarial loss (LSGAN) + Regularizations 적용.

---

4. Experiments

• Coarse voxels로부터 3D shape synthesis, point cloud로부터 3D reconstruction 수행.

---

5. Conclusion

• Implicit & explicit representations 각각의 이점을 모두 수용한 novel 3D representation 제안.

---

Summary

1) Point cloud 혹은 coarse voxelized shape로 입력된 3D shape로부터,
2) PVCNN encoder로 tetrahedral grid에 대한 feature volume을 계산한 뒤,
3) MLP로 해당 grid에 대한 SDF 값과 refinement를 위한 additional feature 계산.
4) 이로부터 surface tetrahedra를 구분하여 graph를 구성하고,
4) GCN으로 grid 좌표와 SDF 값에 대한 offset을 계산하여 update한 뒤,
5) Surface tetrahedra에 한해 volume subdivision step과 additional surface refinement step을 거침.

*Surface tetrahedra로 graph를 구성해 GCN을 활용하는 점이 인상 깊다 :)