강화학습기초(3) - Monte-Carlo Learning

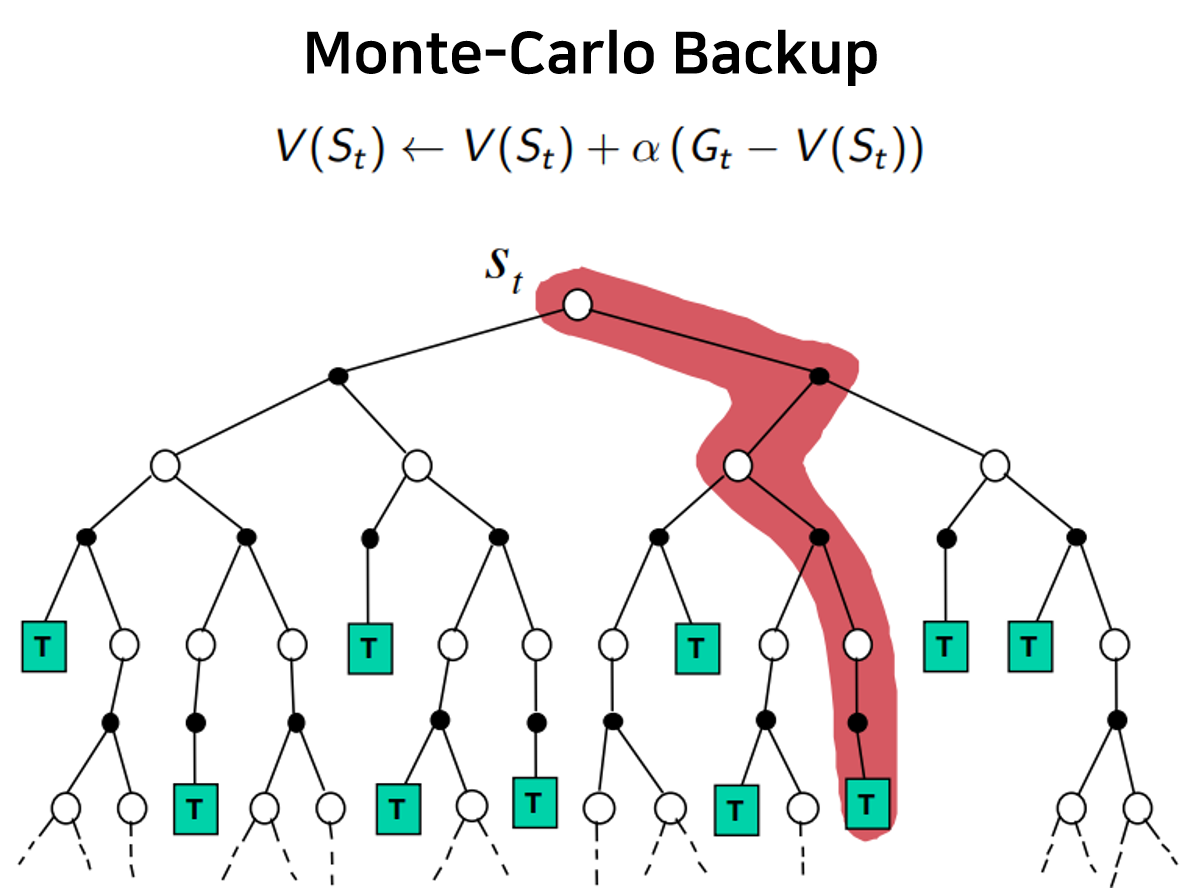
본 글에서는 RL의 첫 번째 learning 방식인 Monte-Carlo learning (MC)에 대해서 알아보도록 한다.

앞서 살펴본 dynamic programming은 MDP에 대한 모든 정보를 알고 있어야 하는 planning 기법으로, 정보가 부족하거나 MDP가 상당히 큰 실생활에 적용할 수 없다. 이에, 다음 state를 임의로 sampling하여 얻어낸 reward 값으로 prediction (planning에서의 evaluation)을 수행하는 sample backup 방식이 바로 Monte-Carlo learning이다.

• Sample backup : 특정 episode와 그에 대한 reward에 대한 sampling 값으로 episode 경로 상의 value function만 update하는 방법
• Full-width backup : MDP의 모든 경우의 수를 모든 state에 대한 value function을 동시다발적으로 update하는 방법

Monte-Carlo Learning

먼저 'Monte-Carlo'라는 명칭은 무엇인가를 random하게 측정하는 경우에 쓰인다. 여기서는 prediction에 쓰이는 episode가 random하게 sampling된다. DP에서의 evaluation, improvement와 같이, prediction과 control의 단계로 나누어보면 다음과 같다.

First-Visit Monte-Carlo Policy Prediction

우선 DP의 policy iteration에서와 같이 초깃값은 zero-initialized value function과 random policy로 둔다. 이후, initial state $s_0$부터 시작하여, 현재의 policy $\pi$를 따라 다음 state를 하나씩 sampling 해나간다.

Agent가 최종 state에 도달하여 하나의 episode가 완성되면 역방향으로 훑어가며 지나온 각 state에서의 return 값을 계산하여 value function에 반영한다. 예를 들어 임의의 state $S_t$에서 $T$ time-step 후 최종 state $S_{t+T}$에 도달했을 경우, $S_t$의 value function에 반영되는 return 값은 아래와 같다.

이 때, 단일 episode 내에서 동일한 state를 여러 번 방문할 경우, 첫 번째 방문에 대한 return 값만 고려하는 first-visit MC와 모든 return 값에 대해 update 해주는 every-visit MC의 방법 등으로 나뉘게 된다. 두 방법 모두 충분한 iteration을 거치면 true value function으로 수렴하지만, 본 글에서는 비교적 보편적으로 연구되어 온 first-visit MC에 대해서만 다루도록 하겠다.

반면 여러 episode에서 동일한 state를 방문하는 경우도 발생하는데, 이 때는 각각의 value function을 평균 내어주면 된다.

예를 들어, 임의의 episode에서 time-step $t$에 처음 방문한 state $S_t$가 있다면, counter $N(S_t)$ 값을 1 증가시켜주고, total return $S(S_t)$ 값을 $G_t$ 만큼 증가시켜준 뒤, $S(S_t)/N(S_t)$의 값을 $V(S_t)$에 대입해주는 것이다.

위 대입값을 return $G_t$에 대해 풀어쓰면 아래와 같은 incremental mean 관계식이 나온다. $S(S_t)/N(S_t)$의 형태가 여러 return을 모아놓고 한 번에 평균을 취하는 것이었다면, 새로운 episode에 대한 return을 기존의 total 값에 그 차이만큼 더해가는 관점으로 생각해 볼 수 있다.

이 때, iteration이 진행됨에 따라 커지는 $N(S_t)$의 값을 아래와 같이 $\alpha$(step size)라는 상수값으로 고정시켜줄 수 있는데, 이는 MC가 매 iteration마다 policy가 바뀌는 non-stationary problem이기 때문에 학습에 효과적이다. 비교적 부정확한 policy로 생성된 앞선 episode에 대해 가중치를 작게 부여하는 것이라고 생각하면 쉽다.

이는 DNN에서의 step size(learning rate)와 동일한 역할을 수행한다.

Monte-Carlo Policy Control

1) Q-value function
만약 DP에서와 같이 state-value function으로 policy control를 하기 위해선 다음 모든 state들에 대한 정보와 해당 state로 갈 수 있는 모든 action들에 대한 이해도, 즉 MDP 모델에 대한 완벽한 정보가 필요하다. 이는 model-free learning을 수행하려는 MC의 목적에 적합하지 않다.

이 때, prediction 단계에서 각 $(state, action)$ 쌍에 대한 Q-value function을 계산해준다면, 각 state에서 Q-value function 값이 가장 큰 action을 택하는 greedy algorithm으로 policy를 수립할 수 있게 되고, 이는 model-free하다.

2) $\epsilon$-greedy algorithm
하지만 위처럼 greedy policy control을 진행할 경우 local optimum에 쉽게 빠질 수 있다. Full-width backup과는 달리, 다른 경로로의 exploration을 충분히 하지 않았기 때문이다. 따라서 아래와 같이, episode를 구성할 때 일정 확률 $\epsilon$으로 Q-value function이 작은 다른 action도 취할 수 있도록 policy를 수정하면 MC의 부족한 exploration의 문제점을 해소할 수 있으며, 이를 $\epsilon$-greedy policy control이라고 칭한다. (임의의 state에서 모든 action을 선택할 확률이 각각 $\epsilon$ 이상인 경우 이를 $\epsilon$-soft policy라고 칭하며, $\epsilon$-greedy policy는 그 중 하나의 종류에 속한다.)

3) GLIE (Greedy in the Limit with Infinite Exploration)
한편 $\epsilon$-greedy 방식의 문제는 충분한 학습이 이루어져도 고정된 $\epsilon$의 확률로 optimal한 action을 선택하지 않게 되어 정확도가 떨어진다는 것이다. 이를 해결하기 위해, $k$번째 control에서의 $\epsilon_k$를 $1/k$로 둔다면 시간이 지남에 따라 non-optimal action을 택할 확률이 0으로 수렴하여 아래의 GLIE 조건을 만족하게 된다.

Greedy in the Limit with Infinite Exploration
$lim_{k\rarr \infin}\pi_k(a|s)=1$
$(a=argmax_{a'\in A}Q_k(s,a'))$

내용을 정리하자면, MC에서는 $\epsilon$-greedy policy를 통해 순차적으로 action을 sampling하여 최종 state까지 도달한 뒤, 해당 episode의 역방향으로 각 state의 Q-value function을 predict한다. 이 때 step size $\alpha$가 고정된 incremental mean 방식으로 새로운 return 값이 반영되며, 이는 앞으로 다룰 다른 학습에도 반복되어 사용되니 기억하자.

이러한 MC는 실제 return 값을 기반으로 prediction이 진행되어 학습의 bias가 낮지만 $\epsilon$-greedy하게 action을 택하는 policy의 randomness 때문에 variance가 높다는 단점이 있다. 또한, episode가 끝나지 않거나 상당히 길 경우에는 학습하기 어렵다는 한계점도 존재한다.

이에, 다음 글에서는 episode가 끝나지 않아도 prediction을 진행할 수 있는 temporal difference learning을 다뤄보도록 하겠다.

---

References

• UCL Course on RL, David Silver
• Reinforcement Learning: An Introduction, Richard S. Sutton
• Fundamental of Reinforcement Learning, 이웅원